对圆柱螺旋运动的别样处理

涂德新

(江西师范大学附属中学,江西 南昌 330046)

常见的螺旋线有抛物螺旋线、圆锥螺旋线、圆柱螺旋线等.其中圆柱螺旋线是一种比较典型的空间曲线,一个动点沿圆柱面的母线做匀速直线运动,同时该母线又绕圆柱面的轴线做匀速转动的合运动的轨迹构成圆柱螺旋线.圆柱螺旋线在生产生活中很常见,绝大多数弹簧也做成圆柱螺旋线的形状.小球沿平面曲线运动很常见,例如小球做圆周运动和抛体运动,但沿空间曲线运动研究较少，本文研究小球在重力的作用下沿空间曲线——圆柱螺旋线运动的规律.

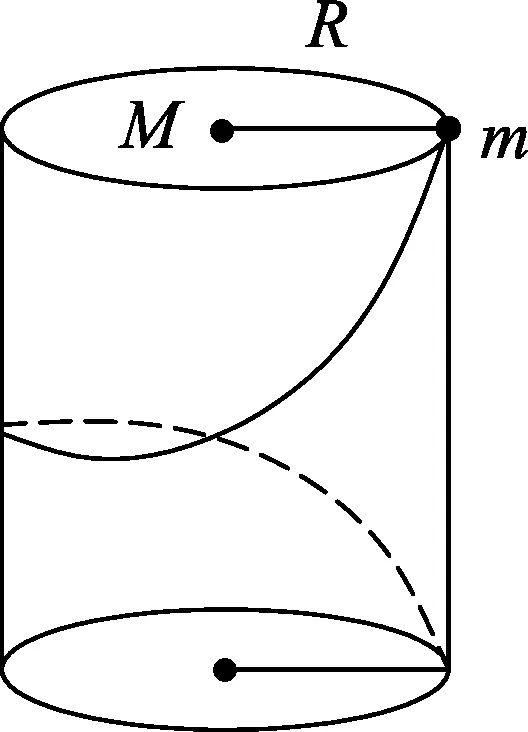
图1

建立模型:如图1所示,一个均匀薄壁圆筒,质量为M,半径为R,在其内侧刻有等距螺旋形沟槽,螺距为2πRtanα,一个质量为m的小球在沟槽的最高点,最初均静止,现释放小球,不计所有的摩擦,重力加速度为g.

问题1:圆筒固定不动,试求小球的速度和受到圆筒的作用力.

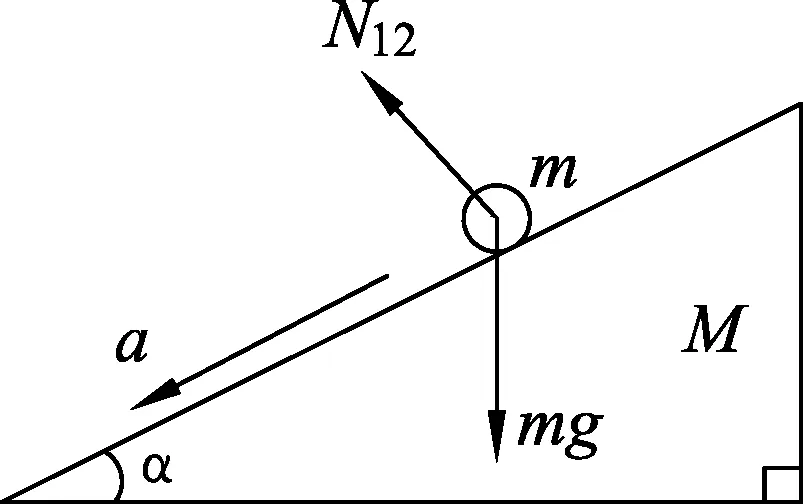
图2

解析:如图2所示,如果将圆筒的侧面打开,发现螺旋形沟槽可以展开成倾斜直线,倾角为α,在垂直于倾斜直线向上的方向上是平衡的,受到的支持力为N12=mgcosα.小球沿倾斜直线的加速度a=gsinα,于是小球的速度为v=g(sinα)t.

考虑小球沿螺旋线的运动,可以分解为水平面内的匀加速圆周运动和竖直方向的匀加速直线运动.指向圆心的弹力充当匀加速圆周运动向心力为

注意到N2=N122+N32,由以上诸式可得圆筒对小球的作用力为

小结:小球沿切线方向只受到下滑力的作用,于是小球的速率随时间成正比,为匀加速曲线运动.小球受到的作用力随时间不断增加.

问题2:圆筒有固定竖直转轴,试求小球的速度和受到圆筒的作用力以及圆筒的运动.

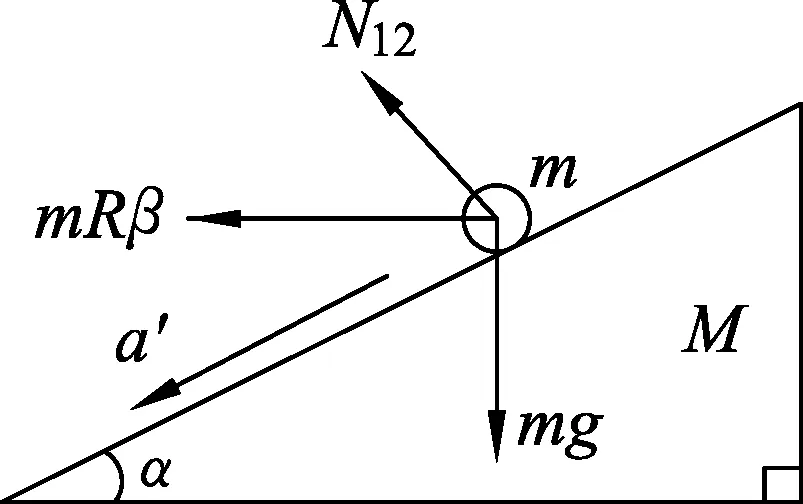
图3

解析:用动力学法处理本问题,如图3所示.将圆筒沿侧面展开,则等距螺旋线展开成倾斜直线,倾角为α,小球受到的支持力为N12,小球相对斜面的加速度为a′.水平速度为vx,竖直速度为vy,圆筒的角加速度为β.

由圆筒相对筒轴的转动定理，有

N12sinαR=MR2β.

(1)

以斜面为参考系,小球受到切向惯性力mRβ的作用,由小球垂直于斜面方向的平衡可得

N12+mRβsinα=mgcosα.

(2)

以斜面为参考系,小球沿斜面方向应用牛顿第二定律，有

mgsinα+mRβcosα=ma′.

(3)

由(1)～(3)式可以求得

进一步求得

考虑到v2=vm2+vy2,可以得到小球的速度为

在圆筒参考中,由于a′为定值,则小球在水平方向为匀加速圆周运动,小球沿水平法向受到两个惯性力的作用,离心惯性力为mRω2,水平切向相对速度引起的科氏力为2ma′tcosαω.设指向圆心的弹力为N3,这3个力的合力充当水平匀加速圆周运动的向心力,即

(4)

将a′、ω代入(4)式可得

(5)

考虑到N2=N122+N32,可得圆筒对小球的作用力为

小结:这种情况下,小球的速率随时间成正比,圆筒为匀加速转动,小球受到的作用力随时间不断增加.

问题3:圆筒放在光滑地面上,试求小球的速度和受到圆筒的作用力以及圆筒的运动.

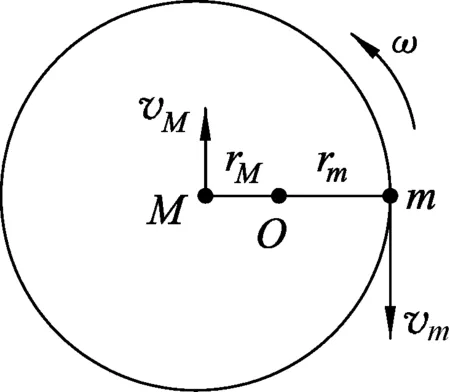
图4

解析:用守恒方程法来处理本问题,某时刻的俯视图如图4所示,小球下降的高度为y,系统在水平方向不受外力,于是系统的质心O在水平方向静止,小球到筒轴的距离不变,于是小球和圆筒均以O为圆心做圆周运动,其圆周半径分别为rm和rM,速度分别为vm和vM,同时圆筒绕筒轴的角速度为ω,小球的竖直速度为vy(垂直纸面向下,图中没有画出).可以得到小球和圆筒的圆周半径分别为

(6)

系统水平方向不受外力,故水平方向动量守恒，有

mvm=MvM.

(7)

相对过质心O的竖直轴,系统的角动量守恒，有

mvmrm+MvMrM-MR2ω=0，

(8)

其中圆筒的角动量为圆筒相对筒轴的角动量和筒轴(圆筒质心)相对系统质心的角动量的矢量和.

地面和圆筒均光滑,系统的机械能守恒，则

(9)

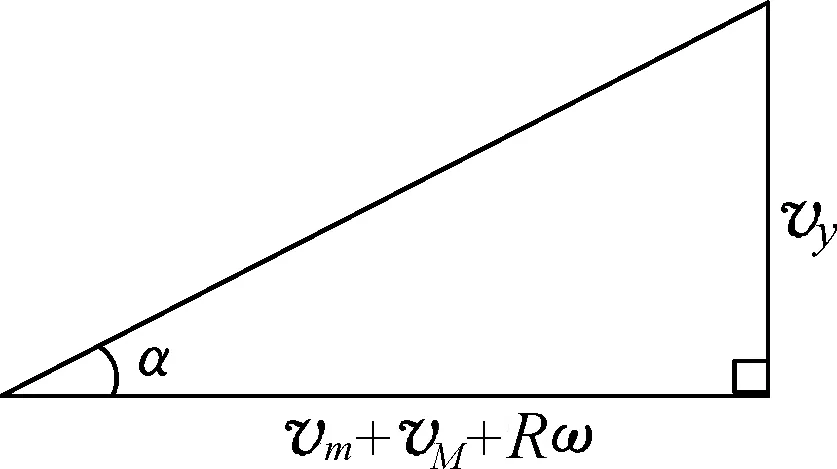
图5

小球相对圆筒为等距螺旋运动,如图5所示,相对速度间存在几何关系为

vy=(vm+vM+Rω)tanα.

利用(6)～(8)式,可以将上式化简为

(10)

由(6)～(9)式可以联立求解得

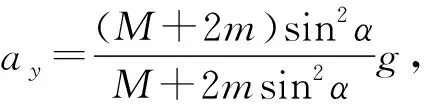
考虑到v2=vm2+vy2,可以得到小球的速度为

下面以地面为参考系来求圆筒对小球的作用力N.

由小球在竖直方向应用牛顿第二定律，有

mg-N1=may,

将ay代入可得

小球在水平方向加速圆周运动，切向应用牛顿第二定律，有

将vm代入可得

法向应用牛顿第二定律，有

将vm和rm代入可得

考虑到N2=N12+N22+N32,可得圆筒对小球的作用力为

小结:这种情况下比较复杂,小球的速率随时间成正比,圆筒绕筒轴为匀加速转动,同时筒轴绕质心轴在平动.小球受到的作用力随时间不断增加.

本文在3种情况下研究了小球沿圆柱螺旋线运动的规律,分别是圆筒固定不动,圆筒有固定转轴,圆筒放在光滑地面上等3种情况,分析相关的数学表达式发现小球的运动全部都是匀加速曲线运动,小球受到的作用力都在随时间增加.第3种情况很特别,结果表明小球的水平分速度和竖直分速度以及圆筒的水平速度和转动角速度都与时间成正比,都是匀加速运动.从物理层面来说也很好解释,圆柱螺旋线展开后的倾角不变,于是小球在竖直面内与圆筒作用力为大小不变的力,作用于圆筒为匀加速平动和匀加速转动.在该力和重力的共同作用下小球做匀加速曲线运动.如果M≫m，可以发现第2种和第3种情况完全等同于第1种情况，这也是很自然的结果.