空间均匀球壳产生引力场蕴含的深层物理思维

贾文静 肖 东

(福建省厦门集美中学,福建 厦门 361021)

类比法作为一种科学研究方法,在物理学中起到重要作用.许多重要的物理规律都是由它引导产生的,例如开普勒的行星运动规律,麦克斯韦电磁场理论,德布罗意波粒二象性理论等等.[1]所谓类比法,它是指具有某些相似性质的两个对象在其他方面也可能具有某种相似的性质或规律,它是一种从特殊到特殊的逻辑推理方法,当然类比法得出的推论是或然的,所有的类比结果都需要严谨的理论认证或实验验证,才能被物理学家接受.

类比法同样在物理教学中也起着关键性的作用,例如万有引力和库仑力的类比教学,比值定义法的类比教学,以及机械振动和电磁振荡的类比教学等等.[2]通过类比法可以使得新旧知识建构联系,不仅能够化抽象为具体,让学生触类旁通,达到温故而知新的作用,并且能够提升学生发现问题、处理问题以及独立解决问题的能力[3，4].

1 引出问题

文献[5]《密度均匀球壳对质点的引力》中,作者用微积分的方法分析了密度均匀的球壳对球壳内外质点所产生的万有引力,得到了如下3个结论: (1) 密度均匀的球壳对球壳内的质点产生的万有引力为0; (2) 球壳对球壳外的质点产生的万有引力等价于质量相同的质点在球心处对其产生的万有引力; (3) 密度均匀的实心球体对质点的万有引力可以认为是密度均匀半径不同的球壳层层叠加,不难得到,在球外的质点受到的万有引力等价于质量相同的质点在球心对其产生的万有引力,在球内受到的万有引力等价于球心到质点为半径的球(内球)所产生的万有引力,当然也就等价于与该内球质量相同的质点在球心处对其产生的万有引力.

这3个结论仍然有许多深层次的问题值得思考,例如,(1) 为什么质点在球壳内所受到的万有引力为0,而在球壳外受到的万有引力却可以将球壳看成质量相同的质点在球心处产生的万有引力,这些等效背后所隐藏的物理机制是什么?(2) 同样的3个结论可不可以对密度均匀的二维圆环适用,如果不适用,那么为什么不适用?(3) 上述的3个推论是一个偶然的结果,还是一个普遍的物理规律,对于其他形式的有心力是否也有类似的结论?

2 万有引力与库仑力的类比

本文用分析类比的方法将万有引力和库仑力相联系,首先,类比库仑力中的电势的概念,我们用引力势的方法回答了第(1)个疑问;其次,类比库仑力中的高斯定理,我们对第(2)个疑问作了详细的讨论;最后,我们将万有引力推广到一般形式的有心力,得到了相应的高斯定理,尤其对两类特别的力(弹性力,1/r形式的力)作了具体的讨论,得到了有趣的结果.这些疑问的解决,不仅能够使学生深刻地把握万有引力和库仑力的联系,更能够突破教学难点,使得其他类似的问题在教学中迎刃而解,有效地提高教学的深度.

2.1 空间引力势分布的求解

万有引力和库仑力是自然界中4种基本作用力的重要组成部分,也是物理教学难点,在电学当中,带电物体之所以能够受到库仑力,是因为源电荷在空间产生了电场.而电场的本质是由于电势的空间分布不均匀性导致的.这种空间的不均匀性在数学上用梯度()表示,即空间中任意一点的电场强度等于在该点电势的负梯度.[6]类比电场强度和电势这两个概念,我们可以定义源质点在空间中产生的引力势不难看出,源质点在空间所产生的引力场强度其中er为径向方向的单位矢量,任意质点所受到的万有引力就等于质点的质量乘以该点处的引力场强度. 因此只要知道空间引力势的分布就能够准确地计算出质点在每一点处受到的万有引力. 下面,我们利用引力势这一概念来回答密度均匀的球壳对其内外质点所产生的万有引力.

图1 问题示意图

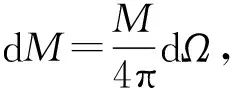
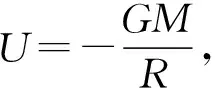
我们接着要追问为什么质点在球壳内所受到的万有引力为0,而球壳外质点所受到的万有引力却可以等价于等质量的质点在球心处对其所产生的万有引力,这里面隐藏着什么物理内涵?联想到电学中的高斯定理,即空间的电场对任一封闭曲面的通量E·dS正比于该封闭曲面所围成的体积内电荷的总电荷量.[6]类比这一定理,我们也可以认为空间当中的引力场强度对任一封闭曲面的通量f·dS正比于该封闭曲面所围成的体积内质点的质量. 这里我们注意到,由于球壳的密度均匀,所以根据对称性原理,我们有理由认为球壳在空间当中所产生的引力势应该具有球对称性. 对于空间中的两点A、B,如果rA=rB,则UA=UB,相应地,如果A、B两点距离球心的距离相同,则它们引力场的大小相等且方向指向球心. 根据这一思想,要求球壳外的一点P处的引力场,我们可以作半径为r的外球,P在球的表面上,在这个外球表面上每一点的引力场大小都是相同的,设为f,方向与外球壳的表面相垂直,则引力场强度对该外球表面的通量正比于球壳的质量. 同样如果将球壳换成质量为M的质点放置于球心处,此时空间的球对称性没有改变,那么由引力场的高斯定理可以看出,球壳在P点所产生的引力场和质量为M的质点在球心处产生的引力场是相同的.而对于球壳内质点在任意位置受到的万有引力为0,那是因为球壳内无引力场,这也很好理解,在球壳内作任意一个曲面,由于在该曲面内没有引力源,所以引力场通量为0.这时只能有两种情况,要么就是均匀的引力场,要么就是引力场为0. 根据引力场的对称性,可以排除前者,所以在球壳内,质点所受到的万有引力为0.

这个引力势需要分两种情况讨论:当r=R时,引力势U为负无穷;当r≠R时,引力势U=-2GMEllipticK(4rR/(r+R)2)/(r+R),其中EllipticK(x)函数是第一类完全椭圆积分函数K(x). 此时,我们注意到,质点在圆环内受到的万有引力并不是0,因为圆环内并不是一个等势体,而在圆环外质点受到的万有引力也并不等于相同质量的质点在圆心处对其产生的万有引力.这一“反常”的结果在于一方面从球壳到实心球是一种线性叠加,但是从圆环到球壳却不能看出是一种简单的线性叠加. 事实上,球壳是由圆环绕其直径旋转而成的,其本质是一种非线性叠加;另一方面在二维平面上,没有类似的高斯定理,即使在圆环内,任一封闭的曲线内部没有引力源,但引力场强度并不为0(r≠0),质点仍然受到万有引力的作用.

2.3 广义中心力场的引力势及其高斯定理

从这一结果我们可以看出,无论力源是否包含在该曲面内,力场对该曲面的通量只与曲面所围成体元的体积大小有关,根据这一高斯定理,我们得到如下的推论:

对于弹性力,密度均匀的球壳对空间任一质点的弹性力,都等效于质量相同的质点在球心处对其产生的弹性力.

具体的证明过程如下,设力源的质量为M,则该力源在空间当中产生的弹性力场为f=-Mr,则相应的势可以写为U(r)=Mr2/2.利用相同的方法,可以求出质量为M的球壳在空间任意一点所产生的力势U(r)=M(r2+R2)/2,相应地,球壳产生的力场f=-Mr,因此上述推论得到验证.

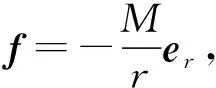
3 总结

本文利用分析类比的方法,重点讨论了密度均匀的球壳对球壳内外质点所产生的万有引力.不仅将之前的结论进行深化,而且对部分结果进行了推广,所有类比的结果都得到了理论严格论证.从这一分析类比法中不仅可以加深对万有引力本质的认识,而且激发学生的求知欲,开拓学生的创新思维,对其他的教学难点也起到积极的借鉴作用.