中学物理实验操作评价研究

邢红军 靳 萱

(1. 首都师范大学 北京 100048； 2. 北京汇文中学 北京 100061)

长期以来,如何对中学生的物理实验操作能力进行有效评定,一直是物理教育界关注的重点课题．由于纸笔测验难以对中学生的物理实验操作能力进行有效考查,就在一定程度上妨碍了中学生物理实验操作能力的发展．有鉴于此,本文对中学生物理实验操作评价指标展开系统的理论研究,期望能够给我国中学物理实验教学的发展以有益的启示．

1 中学物理实验操作评价指标的构建

为了准确考察中学生的物理实验操作能力,需要借助于物理实验．但如何对实验操作步骤赋分,就需要有一把作为标准的“尺子”来丈量．而这把“尺子”,就是中学物理实验操作评价指标．考虑到评价指标的层次性,我们将中学物理实验操作评价指标的构建分为一级指标和二级指标分别加以建构．

1.1 一级指标的构建

中学物理实验操作评价的一级指标,应当结合中学物理实验的特点,遵循简单、易行、可测量的原则,按照实验操作的步骤顺序,对实验步骤进行合理取舍,抓住物理实验的核心要素进行构建．按照这种思路,我们经过系统的理论研究,建构了中学物理实验操作评价的一级评价指标．如表1所示.

表1 中学物理实验操作评价的一级评价指标

1.2 二级指标的构建

依据中学物理实验操作的具体步骤,有必要进一步将各项一级指标进行细化,这就需要建构二级指标．为确保二级指标构建的合理性,我们在研读物理课程标准的基础上,分析其所规定的20项必做物理实验,同时结合已有文献,确定出二级指标,如表2所示．

表2 中学物理实验操作评价的二级评价指标

2 中学物理实验操作评价指标的信度分析

二级评价指标的建构只是中学物理实验操作评价指标建构的第一步,接下来,需要对评价指标进行信度分析,从而保证评价指标的信度．

本研究采用问卷调查法确定各项指标的权重．为使被调查者能更准确的对指标按重要性排序,体现指标间重要程度差异.本研究采用李克特十级量表进行测量．调查对象均为教学论专家、一线教师以及物理教学研究人员．问卷共发放139份,回收问卷139份,剔除24份无效问卷,有效问卷总计115份,有效率为83%．

调查问卷的信度分析,是对调查问卷测量结果一致性的分析．信度越高,表明问卷的一致性越强,结果稳定且可靠．因此,为了了解问卷各变量间的一致性与可靠性,故对问卷的同质性信度进行测量．结果如表3．

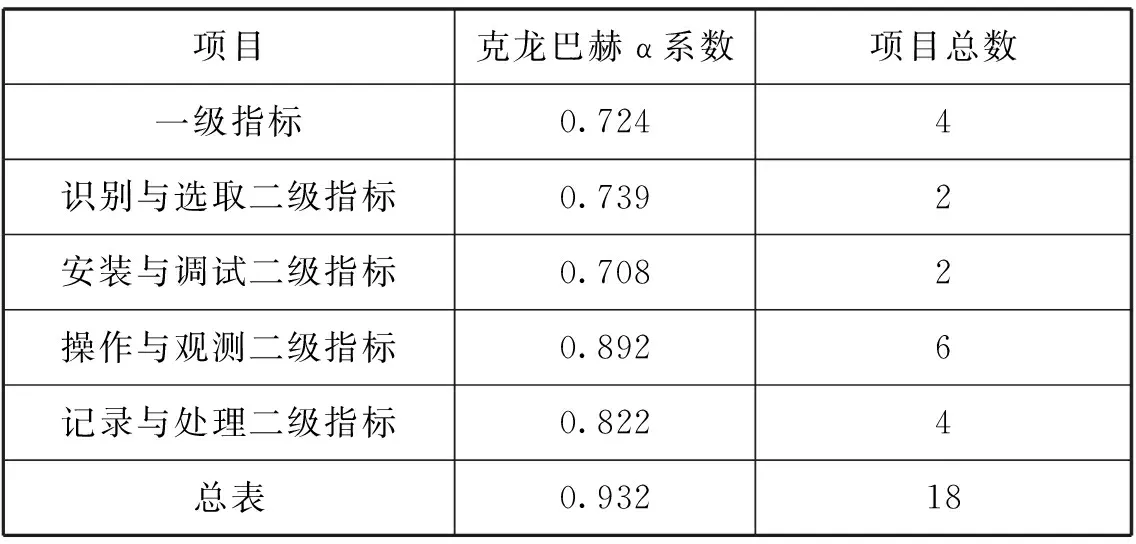
表3 中学物理实验操作评价指标信度分析

如表3所示,一级指标、识别与选取二级指标、安装与调试二级指标的克龙巴赫α系数大于0.7.这表明上述指标内在一致性较好,信度良好,测验结果较为可靠;操作与观测二级指标、记录与处理二级指标的克龙巴赫α系数大于0.8.这表明上述指标内在一致性很好,信度很高,测验结果很可靠;总表的克龙巴赫α系数大于0.9,这表明调查问卷整体内在一致性很好,信度很高,测验结果非常可靠．

值得注意的是,识别与选取、安装与调试的二级指标信度相较其他的指标信度较低,我们认为,这是由于该指标中变量数目较少造成的,变量的多少会影响信度的高低．一般情况下,变量数目增多,信度上升,这与克龙巴赫α系数的计算方法有关．本问卷中,上述两项一级指标分别只对应2个变量,因此信度相对较低．但是,所有指标的克龙巴赫α系数均大于0.7,这表明调查问卷内部一致性较好,可靠性较高．

3 中学物理实验操作评价指标的效度分析

为了使中学物理实验操作评价指标在具体测验中是有效的,需要进一步对评价指标进行效度分析,从而保证评价指标的有效性．

本研究利用SPSS22对问卷的结构效度进行测量．首先对数据进行“KMO和Bartlett球形度检验”,获取KMO值;如果KMO值大于0.5,则可对数据进行因子分析;如果起始特征值大于1.0的变量,其累计解释变异量占比大于60%,则表明问卷结构效度良好．具体因子分析如表4所示.

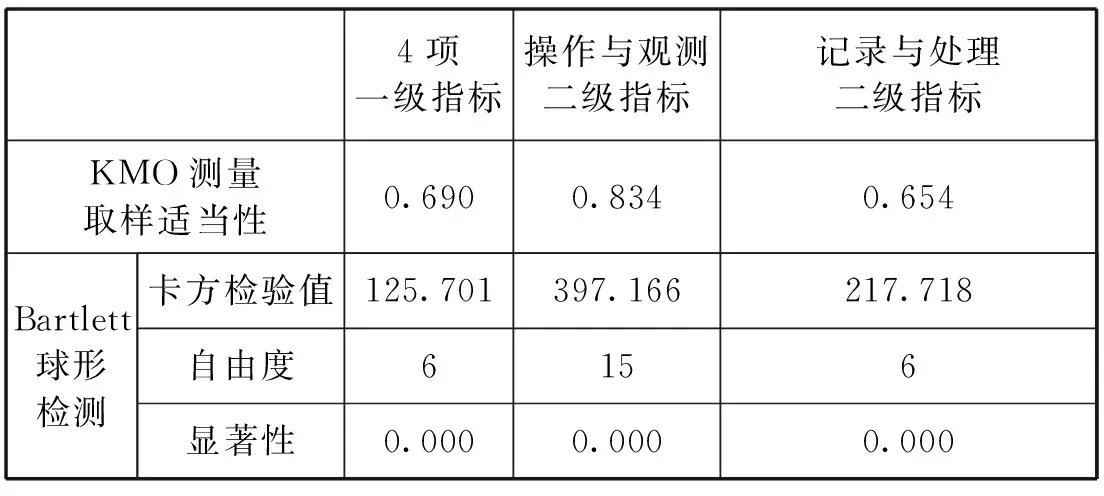
表4 中学物理实验操作评价指标的KMO值分析

由表4可以发现,3项KMO值均大于0.5,故可以对其进行因子分析,因子分析结果如表5所示.

表5 中学物理实验操作评价指标的因子分析

由表5可知,4项一级指标的累积解释变异量为57.766%,大于40%,表明该结果是可接受的．其余两项累计解释变异量大于60%,表明指标的结构效度良好．

4 中学物理实验操作评价指标的权重分析

在对中学物理实验操作评价指标进行信度与效度分析的基础上,还要对评价指标进行权重分析.这是中学物理实验操作评价指标能够应用于实验测验的必要步骤．

权重,表明该指标的重要程度．调查问卷的全部指标权重之和为1,每项指标的权重用小数进行表示．我们将采用调查问卷所获取的数据,借助层次分析法对各项评价指标的权重进行确定．

层次分析法(AHP)是由美国匹兹堡大学教授萨蒂于20世纪70年代初提出,其开创性的把定性与定量的研究方法联系在一起,常用于多目标的决策．该方法的特点为,可以以少量的定量信息为基础,将决策过程数学化,为解决多目标、多准则的繁复问题,给出一套系统、简洁,且高效的决策范式．在使用层次分析法时,需先将待处理的复杂问题拆分为若干层次与因素,并对不同层次与因素进行重要程度的两两比较,之后建立判断矩阵,最后利用判断矩阵的最大特征值与特征向量,得出指标权重．

首先,为了确定两个不同因素的重要性程度,现对标度的选取进行规定,如表6所示.

表6 标度选取的规定

现以4项一级指标的权重计算为例,介绍权重的计算过程．

(1) 确定各指标的平均值.

根据调查问卷的测量结果,一级指标的平均得分如表7所示.

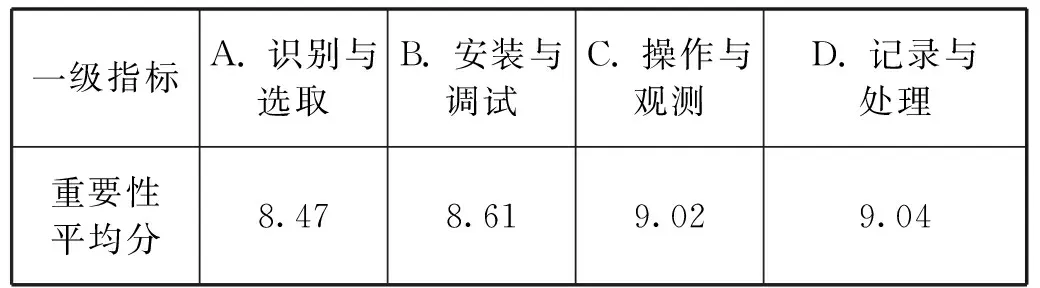
表7 各项一级指标的重要性程度平均得分

(2) 确定判断矩阵.

由表7可以发现,D的重要性程度平均得分最高,值为9.04．现用D的分数与A的分数做差得0.57,介于0.5与0.75之间,故标度取值为4,意为“D相较A明显重要”．根据上述方法,依次判断出D与B、C的标度,填入判断矩阵当中．一级指标的判断矩阵A如下所示:

(3) 计算各个元素的权重.

① 对上式利用算术平均法进行权重的计算,得到最终的权重向量W(亦称为最大特征值对应的特征向量):

(4) 检验判断矩阵的一致性.

表8 一致性指标RI数值

如果数据的一致性比例系数CR<0.10,则认为判断矩阵的一致性较好,结果

能够被接受．

③ 用判断矩阵A乘以权重向量W,再根据AW=λmaxW求出最大特征值λmax,因此CI=0.007．由于判断矩阵A为4阶矩阵,查表可知RI=0.89,则CR=0.01．由于CR<0.1,故判断矩阵A一致性很好．

根据上述计算方式,最终得出中学物理实验操作评价各项指标的分值分配,如表9所示.

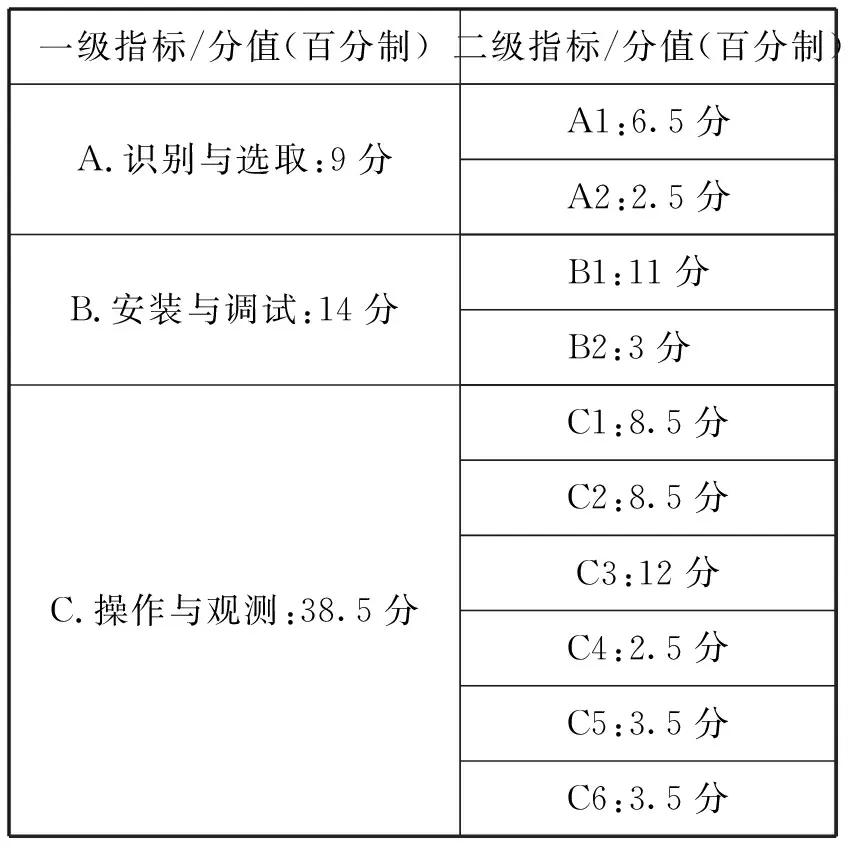
表9 中学物理实验操作评价各项指标的分值

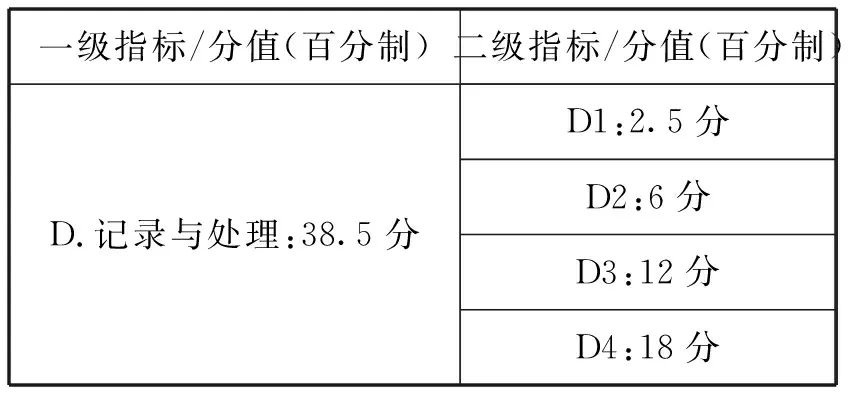
续表

至此,中学物理实验操作评价指标的理论建构完毕．评价指标经过信度、效度检验与权重确定后,就成为一个标准的中学物理实验操作评价指标,可以用来指导中学物理实验操作的评价．显然,这样一个标准化的中学物理实验操作评价指标,就具有重要的理论价值与实践价值．