小学低段计算教学中思维活动经验的有效积累

徐 炎

如何在低段计算教学中培养学生的思维能力，让学生通过参与计算活动积累有效的思维经验，为进一步的学习和发展奠定基础，是每位数学教师尤其是低段数学教师需要思考的问题。以下结合浙教版新思维《数学》教学实践，谈谈自己的体会。

一、学具操作，积累思维活动经验

心理学研究表明，多感官参与学习更有利于习得知识。学习时如果靠动手操作经由脑部活动，可以保留学习获得知识的70%～90%；如果靠口语经由脑部活动，将可保留50%～70%；如果视觉和听觉并用，经由脑部活动，可保留30%～50%；只靠视觉和脑部活动，只能保留20%～30%；只靠听觉学习和脑部活动，只能保留10%～20%的知识。因此教师要在数学教学活动中给学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解并掌握基本的数学知识与技能、数学思想与方法，获得广泛的数学活动经验，不断提升思维的有效性。

教学片断1：浙教版《两三位数除以一位数》

师：这幅主题图讲了一件什么事？有哪些数学信息？你能提出一个怎样的问题？

生：三（1）班、三（2）班各需要多少顶帐篷？

师：你能用线段图来表示关于三（1）班的数学信息和问题吗？

师：谁来列算式？

生：45÷3=？

师：大家能用以前学过的方法计算吗？

生：从 30÷3=10，15÷3=5 得到45÷3=15。

师：能用已经学过的方法解决新问题很不错。现在我们一起来用分小棒的方法，算算这道题。

师：回顾分小棒的过程，能不能用前面的算式来说一说？

生：4捆小棒中取出3捆，平均分成3份，每份1捆，相当于30÷3=10；剩下的1捆拆开和5根合在一起，再平均分成3份，相当于15÷3=5，合起来就是15。

师：对，这个过程我们还可以这样表示。

学生操作可以是具体的、可触摸的学具，也可以是在纸上圈一圈、画一画。通过操作使静态的、形式化的数学符号变得动态、直观，学生能更好地理解符号的意义和运算的意义。教师要善用教具、学具设计有效的活动，在计算时给学生提示性的思考途径，诱发有理有据的思维过程。

二、符号表述，外显思维活动经验

数学是一门抽象的学科，是研究数量关系和空间形式的科学。数学的本质是概念和符号，并通过概念和符号进行运算和推理。数学符号是数学的基本语言，是进行数学思维和开展数学交流的工具。

教学片断2：浙教版三年级上册《图形算式》

师：（出示例题：△×6+175=577）谁能读一读这个算式？

生：△乘以6再加上175等于577。

生：△乘以6的积，再加上175，和是 577。

师：同学们，你们更喜欢谁的读法，为什么？

生：我更喜欢第二位同学的读法，因为从他的读法中，我们知道了△乘6是一个整体，要先算出积，再用“积”去加上175，最后是求出两个数的和，说明了它们之间的关系，所以我更喜欢第二位同学的回答。

师：老师如果写这样一个算式，你们还能读一读吗？

［出示：87÷（△－12）=3］

生：87除以△减去12的差，商是3。

师：同学们真厉害！现在请你们把△×6+175=577这个算式用线段图来表示，能行吗？可以同桌或小组交流。

（学生交流、绘图）

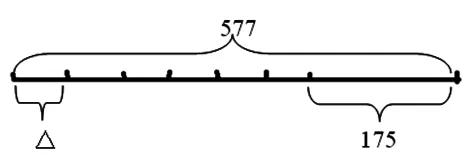
师：看图说说每部分的意思。

生：577表示总数，175表示其中一部分，而△的长度有6条，因此这个题目△应该等于（577－175）÷6=67。

这样的计算教学，通过图形、符号等数学语言表述，能使学生透彻理解数量关系，同时又训练了其口头表达能力，更重要的是锻炼了学生的思维能力。符号表述不仅在学生数学学习的过程中对数学世界的描述、规律揭示和概括、问题的解决具有重要的作用，而且还将作为学生数学素养的一种表现形式，体现着学生的综合素养。

三、联系生活，激活思维活动经验

小学数学计算教学中的知识虽然不深奥，但是却与生活实际息息相关。教师要学会有效联系，将一些数学计算规律与生活现象结合起来，帮助学生更好地理解、记忆，同时也训练其思维的深度、广度和灵活性。

教学片断3：浙教版四年级上册《商的变化规律》

师：（出示探究单）计算下面三组题，你发现了什么？

生：通过观察和计算，我发现了第一题除数不变，被除数变大了，商也变大了，而且变大的程度是一样的。

生：我发现第二题被除数不变，除数变大了，商反而变小了。说明除数乘以一个数，商却除以这个数。

师：你们的发现真了不起，第三题和前两题又有什么不同呢？

生：第三题是被除数和除数同时乘以一个数，可是它们的商是不变的。

师：刚才我们通过对算式的观察研究，发现了商的变化规律，其实在生活中，也不乏这样的规律，你能举举例子吗？

（学生通过小组讨论，交流汇报）

教材的例子相对抽象，“从上往下看，除数不变，被除数乘几，商也乘几；从下往上看，被除数除以几，商也除以几”，部分学生较难理解，或容易忘记。而将商的变化规律与生活情境建立联系，运用生活中的数量关系来支撑理解，遵循“实践——认识——再实践——再认识”的认知规律进行教学，沟通和激活思维，起到事半功倍的作用。

四、拓展运用，深化思维活动经验

数学计算与解决问题之间是相辅相成而不是独立存在的。计算是解决问题的手段，解决问题是计算的目的。给简单的计算搭建生活原型，让学生在解决生活问题的过程中能更好地认识数学内涵本质、建构数学模型、深化思维活动经验。

教学片断4：浙教版三年级上册《智慧乐园一》

师：想一想，你能用学具（或图形）把上面的这幅图的意思表示出来吗？

师：画图的方法可以帮助我们知道桌子和人数之间的关系，接下来我们就边画图边填写表格。

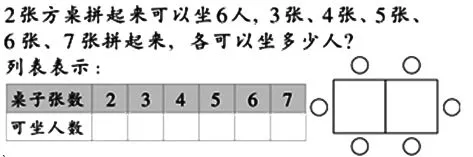
（学生边画边填写）

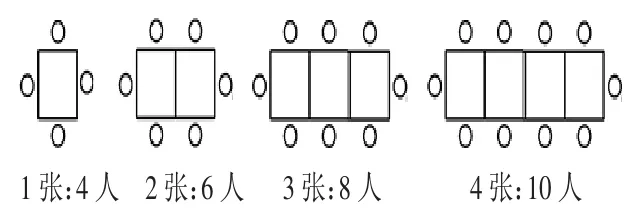
师：刚才通过画画，我们知道了 1、2、3、4 张桌子分别能坐下的人数。讨论一下，桌子数和人数之间有一种什么关系呢？

生：每张桌子的上、下两边一共可以坐2人，最后再加上左、右两边的2人，因此人数就是桌子数乘2再加2人。

师：如果有11张桌子，你不画图，能知道可以坐几人吗？15张、24张呢？

生：11 张桌子：11×2+2=24人；15 张桌子：15×2+2=32 人；24张桌子：24×2+2=50 人。

师：想一想，人数和桌子数之间有什么关系？

师：如果人数用字母a表示，桌子数用字母b表示，你还能用一个算式表示吗？

生：a=b×2+2。

师：如果可以坐34人，你知道用了几张桌子吗？

生：把左右两人去掉，再平均分成2份，就是桌子数。

生：（34－2）÷2=16（张）。

生：（a－2）÷2=b。

……

小学生的思维处于以具体形象思维为主，逐步向抽象逻辑思维过渡阶段。在教学过程中，通过让学生画一画的方法，把抽象的题目具体化、形象化，使学生看得清、摸得着、想明白，帮助学生在丰富的感性认识的基础上，加以比较、分析、抽象、概括，建立人数、桌子数的模型：人数=桌子数×2+2；桌子数=（人数－2）÷2。