线段有限长思维无极限——《认识线段》教学设计（一）

王小波

【教学内容】

人教版二年级上册第一单元，第 2～10 页。

【教学过程】

一、活动引入，激活思维

师：老师这里有两根毛线，一根是红色的，一根是蓝色的。你能想个办法比出哪根毛线长一些吗？你的方法是什么？

生：把两根毛线拉直，再把一端对齐比较。

师：好，请两位同学到前面来比比看。哪根长？

生：（经过拉直比较）红毛线长一些。

【设计意图：数学的核心价值是“数学的思维方式”。通常的做法是让学生把弯曲的毛线机械地拉直，从而揭示“线段是直的”这个特征，此时学生的思维是被“牵着走”的。而本课设计中，采用两根毛线比长短的方法，学生自然想到要“化曲为直”，这是真实的需要，也是发展学生高阶思维、培养学生解决问题能力的需要。】

二、建立模型，聚敛思维

1.揭示线段特征。

师：我们来研究这根红毛线，像大家说的这样，把线拉直，两手之间的一段在数学上就可以看作一条线段。（板书：线段）

师：如果竖着放，两手之间可不可以看成线段？斜着呢？

生：不管怎样摆放，两手之间都可以看成线段。

师：没错！同学们再看，（捏住线段的一段）两手之间的这一段可以看成线段吗？

生：可以的，现在的线段比刚才更短了，还可以把线段变更短。

（学生上台操作）

师：是的，这说明线段是有长有短的。我们把线段请到屏幕上。（出示PPT）瞧，这就是一条线段。你觉得线段是什么样的？

生：线段是直的。（板书：直的）

生：有两条小竖线。

师：这两条小竖线表示这条线段从这头到那头，在数学上这两头一般用短短的小竖线表示。这叫线段的端点，线段有几个端点？（板书：两个端点）

师：现在，你知道线段是什么样的了吧？

2.学画线段。

师：你们谁可以在黑板上画一条线段？

（一位学生在黑板上画线段）

师：评价一下，他画得怎么样？

师：你们也想画吗？拿出水彩笔，在白纸上试一试。

（学生画，教师巡视，搜集不同素材进行展示）

师：（展示学生作业）看看这些作业，你有什么想说的？

生：这几幅作业都是线段。

生：这几条线段都是直的。

生：这几条线段都有两个端点。

师：你们说了它们的相同之处，那它们有什么不同的呢？

生：它们的颜色不同，长短不一样，位置也不同。

师：尽管它们颜色、长短、位置都不一样，但都是直的，有两个端点，所以都是线段。

3.判断图形。

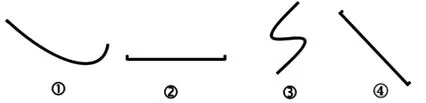
图1

师：（出示图1）这几个图形都争着说自己是线段，你能当小裁判来判断一下吗？

生：①③不是线段，②④是线段。因为①③都是弯的，所以不是线段；②④都是直的，且都有两个端点，所以是线段。

4.图形中的线段。

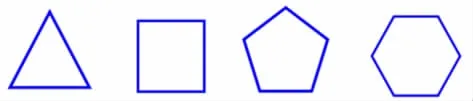
图2

师：（出示图2中的三角形）这是一个？三角形上有线段吗？

（学生上台指一指三角形上的线段）

师：（指其中一条线段）你说这是线段，那这条线段的端点在哪里呢？

生：就是三角形的顶点。

师：是的。当两条线段相接时，它们相接的那一点就是它们的端点。

师：三角形是由几条线段围成的？

生：（异口同声）三条！

师：（依次出示正方形、正五边形、正六边形）这是什么图形？正方形是由几条线段围成的？正五边形是由几条线段围成的？如果你是老师，接下去你会出什么图形？

生：正六边形，这是有规律的，图形的边数依次增加“1”。

师：仔细观察，还有什么发现？

生：几边形就有几条线段围成！

【设计意图：线段的显著特征是直的、有两个端点。在此基础上，通过拉直毛线的长短不等，让学生进一步感受线段的特征。画线段，不只是让学生一画了之，还需在学生画完后，通过比一比找出相同之处和不同之处。学生的辩证思维就是在一次次的“多想一步”中培养出来的。而后，层次分明的两个练习：判断练习是对线段特征的进一步强化；图形中的线段意在引导学生进行数学思考，“几边形就有几条线段围成！”如此凝练的语言由学生说出，也是在帮助学生建立较为完整的线段概念。在整个概念建立及巩固的过程中，教师都重视让学生去表达、阐述、评价、分析等等，学生的高阶思维能力得到充分地发展。】

三、尝试创造，延展思维

师：（拿出不规则纸片）同学们，这是一张不规则的纸，不用直尺也不用笔，你能想个办法创造一条线段吗？

生：（独立折一折后展示）折痕就可以看作线段。

师：看来，线段可以画出来，也可以折出来。同桌两人比一比，看谁折出的线段长？

师：接下来，提高要求，你能折出这张圆形纸上最长的线段吗？

（学生上台比一比）

生：我把这张纸对折，就能找到圆形上最长的一条线段。

师：这条重要的“线段”，我们将来还会好好研究呢！看来，数学就在我们身边，只要多留心思考，一定会有收获。

【设计意图：“儿童的智慧在他的手指尖上。”纸片上本没有线段，学生通过想象，从无到有，动手折出了一条条线段。作为一种高阶思维，“创造力”在学生手脑并用中得以迸发。接着，“折出最长的线段”，对学生的思维又是一次挑战。猜测、尝试、验证、比较等等，在最后的交流中，学生的思维不断深入，获得自由的放飞。】

四、关注德行，提升思维

师：（出示图 3）星期天，小猫去小狗家玩，它有三条路可以选择。如果你是小猫，你会选哪条路呢？为什么？

生：我会选②，这条最近的路线就是一条线段。

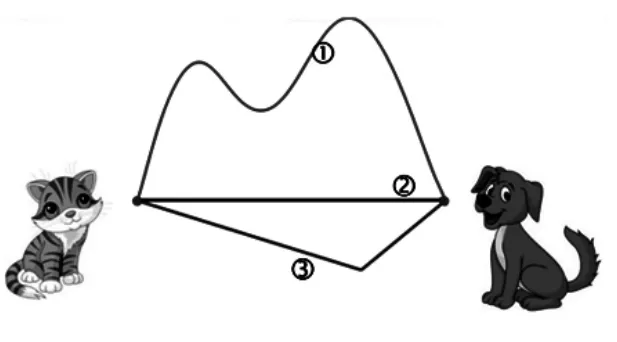
图3

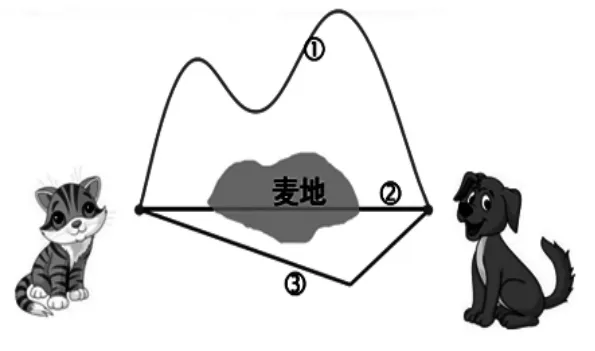
图4

师：（出示图4）过了一段时间，大象伯伯在它们两家之间种上了一片麦子，现在小猫去小狗家，选哪条路呢？为什么？

生：这次我会选③，②虽然是最短的，可是如果选②就会践踏麦地，所以我不选！

师：看来，虽然两点之间线段是最短的，但在生活中，我们还要考虑实际情况，爱护庄稼。

师：同学们，今天学的线段不仅生活中能用到，它也与数学上的一些规律有关。（出示PPT）瞧，连接任意两点，可以画几条线段？在练习纸上画一画。

生：连接两点只能画一条线段。

师：三个点，连接每两点，能画几条线段？连成了一个什么图形？四个点呢？自己试一试。

（出示图5，展示学生作业）

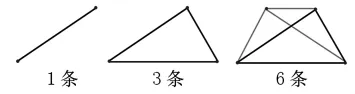
图5

师：连接四个点时，怎么有的同学画出了四条，有的同学画出了六条呢？

生：画四条的同学少连了中间的两条，应该是每两点都要连接起来。

师：怎样才能不重复、不遗漏呢？

生：可以给每个点标上序号，依次连接。

师：每增加一个点，都要和之前的每一个点相连。

师：如果再多一个点，五个点呢？六个点呢？这里还有一个很有意思的规律，课后可以研究一下。

【设计意图：连接两点形成一条线段，再延伸到三个点、四个点、五个点……帮助学生建立“有序”的思维模式，由课内延伸到课外，再去探寻其中蕴含的规律，有利于培养学生的逻辑思维能力，让学生的学习品质得以提升。当然，数学教学，除了教学知识、提升思维，还需要关注人的德行发展。用小动物的口吻，让学生体悟到：数学是“全人”的教育。】

五、全课小结（略）