基于引导滤波和shearlet稀疏的遥感图像融合算法

王 威，张佳娥

(1.长沙理工大学计算机与通信工程学院，湖南 长沙 410114;2.综合交通运输大数据智能处理湖南省重点实验室，湖南 长沙 410114)

1 引言

随着智能传感器技术的迅猛发展，遥感卫星平台获取到的遥感信息愈加丰富。多个卫星平台传感器针对同一地点进行成像时，所拍摄的图像集会存在信息重叠或不同信息可以互相补充的情况。因此，在一般情况下，高空间分辨率和高光谱分辨率难以共存，需要通过融合处理来实现。在传统的融合方法中，小波变换[1]以其计算效率高和多分辨率分析的优势，得到了广泛应用。但是，小波变换在图像方向信息的获取上有一定的局限性。Shearlet变换[2]的出现充分弥补了这一缺点，能有效地捕获图像的几何结构信息。由于shearlet变换的基函数是固定的，很难适应遥感图像的复杂结构，稀疏域模型[3]为此提供了新的解决视角，此模型是直接对原始图像在单尺度下进行稀疏化，可以获取到原始图像的明显特征，但不能多尺度[4]分析数据。2010年，胡建文等人在IHS变换的基础上引入稀疏化表示，提出了融合算法，但该算法使用的是DCT(Discrete Cosine Transform)字典，不能准确表达出图像细节。本文充分结合shearlet变换和稀疏域模型的优势，分离出低频和高频部分，以自适应字典和局部特性为着重点，能更好地对遥感图像的基本特性进行研究。

从根本上来说，原始的多光谱图像在不破坏自身光谱信息的情况下，需要吸纳全色图像所提供的空间细节信息，以达到融合的目的。在融合过程中，全色图像和多光谱图像可进行一定的预处理，促使最终的融合图像信息保留更为完整。同样，在多尺度变换与稀疏表示结合的融合模型中加入优化处理，在进行整体融合之前加入拟合预处理。传统的拟合预处理通常从图像整体考量而忽略图像局部信息之间的联系，如直方图匹配[5]和SFIM(Smoothing Filter-based Intensity Modulation)优化滤波[6]。2013年，引导滤波[7]模型被提出，它是以导向图像为指引，对输入图像建立起当前像素点与邻域像素之间的线性模型，从而完成整个滤波过程。本文利用引导滤波进行预处理，缩小亮度图像以及全色图像的图像差异。其次用shearlet变换结合稀疏变换，稀疏化处理低频子带系数，经处理后的子带系数通过l1范数即以图像块活跃度取较大值的标准进行替换融合。基于区域能量和区域方差融合处理对应的高频子带系数，再利用shearlet反变换获取融合结果。

2 Shearlet变换

2007年,由Easley等人[8]提出了shearlet变换，shearlet变换最初是由合成小波的数学模型演变出来的。从本质上来说，shearlet变换存在着多尺度的规律，对母函数做尺度调整以及平移，调整尺度参数以及平移距离的不同取值能得出一组shearlet的基函数，利用基函数对信号进行处理，能多尺度地对信号进行分析。

Labate等人通过对仿射系统理论和多尺度分析理论的理解，提出合成小波的数学表达模型，当维度N=2，任取平方可积的连续函数f,即∀f∈L2(R2)时，式(1)均成立：

(1)

MAB(φ)=φj,l,k(x) =

(2)

从而形成了Parseval紧框架，所提出的φj,l,k(x)就是合成小波。在系统MAB(φ)中，矩阵Aj与尺度变换存在一定的联系，相当于小波变换中的尺度参数，而矩阵Bl与旋转剪切等操作存在相关性。

Shearlet变换则是从上述模型中衍生出来的，若满足以下条件：

，

(3)

则系统MAB(φ)是shearlet变换的表达形式。

在图像融合框架之中，shearlet变换将原始的多光谱图像和亮度图像分解为高频部分和弱稀疏性的低频部分，它与小波变换的不同从根本上而言在于分解方式，原始图像被分解出的高频子带更具有方向性。

3 过完备稀疏表示

稀疏表示即为信号的稀疏化处理，尝试寻找到信号中最少非零元素的线性组合，而过完备稀疏表示[9]是通过过完备字典来处理信号。图像稀疏化表示是以过完备字典D为基础，图像信号以一维向量Z的形式做低维投影，最终获得的投影系数就是稀疏化向量x。稀疏化的数学模型为：

(4)

其中，‖x‖0为x的l0范数，ε为逼近误差。

为了获取最优稀疏系数的值，过完备字典的选择尤为重要。字典的获取可以通过两种方式：第一种使用解析字典，解析字典的训练耗时较短，固定化特征明显，应用图像种类较少，对于复杂图像存在不适应性；第二种采用自适应字典，不以某种特定函数作为基础，而是根据图像特征需求来训练。使用率较高的训练方法是MOD(Method Of Directions)算法[10]和K-SVD(K-means Singular Value Decomposition)算法[11]。本文使用K-SVD算法来训练图像字典，训练字典的最终目标是要获取图像最优稀疏化表示，图像样本块训练目标可表示为：

minD,X{‖Y-DX‖2}

s.t. ∀i,‖xi‖<ε

(5)

Figure 1 Flow chart of the proposed fusion algorithm图1 融合算法流程图

其中，D为过完备字典，其初始设定为固定字典，Y是图像训练样本集，X是稀疏系数矩阵，以第k个原子dk为例，更新时与X中第k行xk作相乘处理，图像样本块训练模型更改为：

(6)

其中，Ek为相对误差，dj为字典D中的第j列。K-SVD算法的核心就是通过不断更新字典中的值，促使训练出来的字典能够具有自适应性，能够更好地处理原始图像。

4 融合算法

本文将shealet稀疏基与引导滤波结合起来构建遥感图像融合框架。该方法首先利用IHS变换将多光谱图像分解为亮度分量图I、色调分量图H、饱和度分量图S。以全色图像做导向图像，通过引导滤波向亮度分量图中注入细节信息做预处理。shearlet稀疏化模型作为主体框架，shearlet变换分解图像为高频和低频部分。低频部分进行稀疏化处理，稀疏过程中采用K-SVD算法训练字典，OMP(Orthogonal Matching Pursuit)优化逼近，以l1范数即图像块活跃度取较大值的标准进行融合，获取最终低频系数。高频系数考量区域特性，以方差和能量做参数，进行融合。最后，shearlet反变换和HIS反变换作用后得到最终融合图像，算法流程图如图1所示。

4.1 引导滤波

引导滤波不同于其他种类的滤波处理方式，它着重于将导向图像的特征注入到输入图像中，对于图像融合来说，以引导滤波作预处理可以更好地保留图像信息。

以亮度图作为导向图像p，全色图像作为输入图像I，滤波输出图像为q,当像素点为k时，存在线性关系：

qi=akIi+bk,∀i∈ωk

(7)

其中，ωk是以当前像素点k为中心、半径为r的邻域区间。ak,bk是滤波函数qi在ωk中的线性系数,其取值是确定的。在滤波过程中，如何取得ak,bk的最佳解是处理的核心。为了更好地优化，引导滤波模型不仅需要满足式(7)中的线性模型，还需要考虑窗口的目的函数：

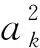
(8)

其中，ε是限制ak上限值的重要参数，从而得出最佳解：

,

(9)

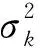
从窗口函数中可以看出，引导滤波充分考虑了邻域范围内其他像素点给当前像素点贡献的权值。同时将全色导向图像的部分图像信息注入到了亮度分量图中，完成了前期预处理所要达到的目的。

4.2 融合规则

4.2.1 低频融合规则

低频部分可看作是图像的逼近表示，但其存在弱稀疏性。针对这一特性，本文拟采用稀疏化模型对全色图像和亮度图像的低频子图分别进行处理，用K-SVD算法训练自适应字典，用OMP求解最优稀疏表示向量。融合规则选择图像块活跃度较大者作为低频子图融合系数。

对亮度低频子图和全色低频子图进行稀疏表示后，获取到编号为i的图像块的稀疏系数分别为Sqi和Spani，图像块活跃度[12]则为：

Vqi=‖Sqi‖1,i=1,2,…,N

(10)

Vpani=‖Spani‖1,i=1,2,…,N

(11)

建立比较函数，选择活跃度较大者作为低频稀疏融合系数：

(12)

4.2.2 高频融合规则

由shearlet变换分解出来的高频部分带有原始图像的细节信息。在高频子图融合规则的选择中，以当前像素点和邻域像素点作基础信息，充分考量局部特性划定局部区域。

根据高频部分的特征，采用区域方差与区域能量[13]相结合的融合规则：

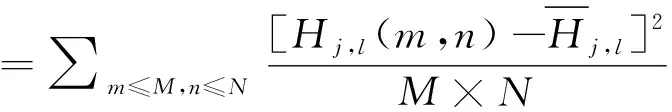
(13)

Ej,l(m,n)=∑m≤M,n≤NHj,l(m,n)2

(14)

Rj,l(m,n)=a×Dj,l(m,n)+b×Ej,l(m,n)

(15)

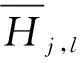
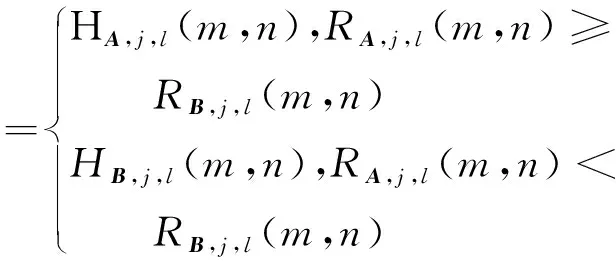
(16)

5 实验分析

本节进行两组对比实验，说明融合算法的优化性。两组对比实验原始图像是在不同地点成像的，初期图像配准已完成。实验环境为CPU主频2.50 GHz，内存4 GB 的 PC 机，Matlab2011模拟编程获取融合结果。

在两组实验中，实验设置参数如下：原始图像大小均为256×256，引导滤波邻域窗口半径r=3，ε=1×106。Shearlet 变换的分解参数设为{2,3,4,4}。在低频系数融合过程中，根据经验，利用K-SVD算法分别训练字典，利用与实验图像同类型的遥感图像作为样本图像，滑窗技术最合适的窗口大小为8×8，因此随机选取样本图像50 000张，样本图像块大小为8×8。迭代次数以100为准，字典大小为64×256，冗余度控制因子为4。在高频系数融合过程中，邻域大小M×N=3×3，权值a=b=0.5。

本文主要和三种方法进行对比：IHS变换[14]、小波变换与稀疏化模型结合的遥感图像融合算法WT-SR(Wavelet Transform Sparse Representation)[6]和shearlet稀疏基融合框架算法shearlet-SR(Shearlet Sparse Representation)。

第一组实验选取的图像具有一定的图像采集特征性，采用的是多传感器图像融合方法，全色图像和多光谱图像分别来自法国地球观测卫星以及美国陆地卫星的主题制图仪。针对同一场景不同成像模式下选取的全色SPOT图像以及多光谱TM(Thematic Mapper)图像,与传统融合算法以及其他新型融合算法进行对比，实验结果如图2所示。

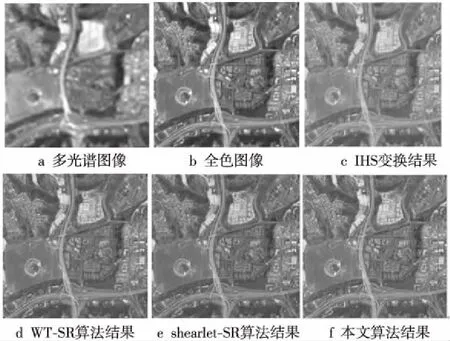
Figure 2 Results of fusion experiment 1图2 融合实验结果1

第二组实验图像是北京某地区的遥感图像，全色图像和多光谱图像在采集图像时均是该场景之下采集的，具有一定的地区特征性。与传统融合算法以及其他新型融合算法进行对比，实验结果如图3所示。

Figure 3 Results of fusion experiment 2图3 融合实验结果2

根据图2的融合结果,从主观上来看，本文算法主观感受最为清晰，空间细节表征明显，光谱信息的保留程度以及色彩的均匀程度最佳。与图2c的IHS算法结果相比较，本文算法光谱信息丢失率较低。WT-SR算法是在传统的HIS算法上增强了图像融合效果，图2d达到一定清晰度的要求，但与图2e相比，本文算法还存在一定的视觉差别。在光谱细节以及清晰度方面,shearlet-SR算法没有本文算法融合图像质量高，印证了引导滤波的作用。同样，通过实验2的图像主观评价也可以得出这一结论。

本文算法的优越性不仅以主观视觉来判别，为了得到客观的评价结果，采用下述图像评价参量[15]来评价图像质量:

(1)峰值信噪比PSNR(Peak Signal Noise Rate);

(2)标准差SD(Standard Deviation);

(3)相关系数CC(Correlation Coefficient);

(4)光谱角SAM(Spectal Angle Mapper)。

两组实验的图像评价参量如表1和表2所示，图像评价参量就代表着融合图像质量的优劣。根据数值评测，峰值信噪比以及标准差衡量图像对于细节信息的保留程度，其数值越大，表示全色图像特征注入到多光谱图像中的成分越多，图像清晰度越高。本文算法在表1和表2中的值均优于其他算法。相关系数和光谱角分别用于衡量图像与原始图像的相关性以及光谱畸变率。从第3、4行数据中可以看出，本文算法相关系数值偏大，光谱角数值偏小，说明本文算法能在保留多光谱图像的光谱信息的情况下提高空间分辨率。

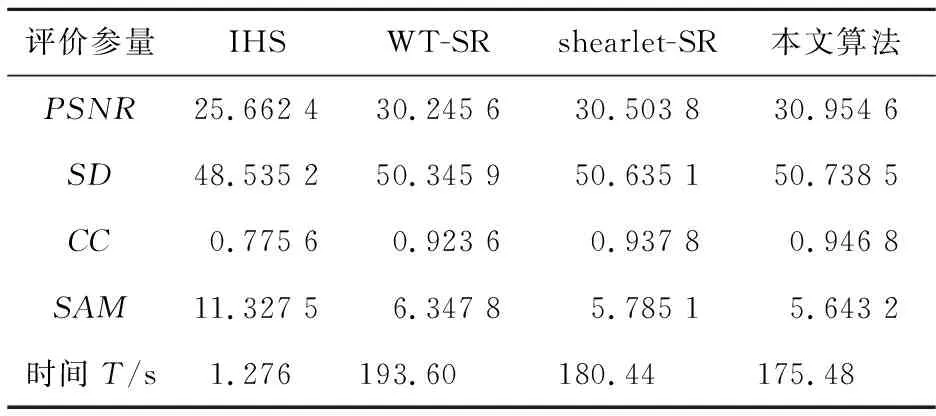
Table 1 Performance analysis of experiment 1

Table 2 Performance analysis of experiment 2

算法除了其有效性之外还需要考虑算法的实现效率，本文采用运行时间T来进行算法效率对比。传统算法一般是采用简单的替换分量的方式，效率高，但会造成严重的图像信息缺失。而加入稀疏表示后，稀疏化处理阶段会有时间上的损耗，但本文算法在经过预处理导向滤波和shearlet变换分离高低频的作用后，运行时间缩短了。因此，与WT-SR算法和shearlet-SR算法相比，本文算法运行时间较少，提高了融合速度。

实验结果进一步表明，本文算法在遥感图像融合处理过程中，通过引导滤波的优化预处理以及shearlet稀疏化模型的作用能够把所需的光谱信息以及空间信息得以最好地留存，融合所得到的最终的高分辨率多光谱图像可应用于多个遥感领域。

6 结束语

本文的主要贡献是将shearlet变换结合稀疏表示导入IHS遥感图像融合模型中，同时应用引导滤波对原始图像进行拟合预处理，引导滤波以导向图为指引，在输入图像中建立起当前像素点与邻域像素之间的线性模型，从而完成整个滤波过程。利用shearlet变换将图像分解为高频子图和低频子图，能很好地提升效率，自适应字典能表示遥感低频图像的复杂结构。

获取到的稀疏系数通过图像块活跃程度取大的标准进行融合处理，得到最终低频融合系数，增强了局部对比度。而高频子图的融合方法充分考量区域特性，采用区域方差与区域能量相结合的融合规则。实验结果表明，本文算法能提高图像清晰度以及光谱保留度，在图像完整度和细节考量上远好于其他对比算法。