一类四阶有理差分系统的动力学行为

，，

(太原理工大学 数学学院，山西 太原 030024)

差分方程是研究离散型变量之间变化规律的有效方法。只要变量的离散值具有某种递推关系，就会与差分方程有所关联，而且离散的差分模型为进行计算机模拟提供了方便。近几十年来，差分方程的理论和应用研究得到了迅猛发展，尤其是在经济、医学、物理、化学、生物学、军事科学等领域。差分方程的理论和应用研究帮助人们解决了很多实际问题。近年来，诸多学者致力于研究高阶有理差分方程的定性性质，并取得了丰硕的成果，这些结果不仅丰富了人们对差分方程的理论认识，同时使得差分方程的应用更加广泛。文献[1-3]中系统、全面地阐述了差分方程的基本理论。 Kurbanli等[4]研究了初值(xi,yi)≥0(i=1, 2)的差分系统

其中n∈。对于给定的初值(xi,yi)(i=-1,0)，该差分系统确定唯一的正解序列同时对解序列的性质进行了分析和讨论。Zhang等[5]在初值(xi,yi)(i=-2,-1,0)和参数A、B均为正的条件下研究了差分系统

的正解和平衡点的稳定性等问题。Din等[6]研究了参数α、β、γ、α1、β1、γ1和初值x0、x-1、x-2、x-3、y0、y-1、y-2、y-3均为正实数的差分系统

平衡点的稳定性、不稳定性、全局性以及正解的周期性。Din等[7]研究了参数αi、βi、ai、bi(i=1, 2)和初值x0、x-1、y0、y-1均为正实数的差分竞争系统

正解的有界性、持久性、正平衡点的唯一性、局部和全局行为以及收敛速率问题。Hu等[8]研究了参数a、ai>0(i=0,1,…,k,k=0,1,…),初值x-k,…,x-1≥0,x0>0的差分系统

依赖于参数空间的全局动力学行为。Ignacio等[10]研究了参数a、b为实数，初值(x-1,x0)∈2的差分系统

解的渐近性态和稳定性。

在生态系统中，当世代不重叠的2个种群之间存在着一定的关系(如捕食、竞争、共生、寄生等)时，它们在几代内的数量变化规律可以通过差分方程来较好地描述。在许多情况下，种群某代的数量往往会受到前四代生命活动的影响。本文中对四阶有理差分系统

(1)

的平衡点的存在性及其稳定性、解收敛到平衡点的速率和阶-2周期解的存在性等问题进行研究，其中参数a、a1、b、b1、c、c1及初值(xi,yi)(i=-3,-2,-1, 0)均为正实数。

1 解的正性与收敛性

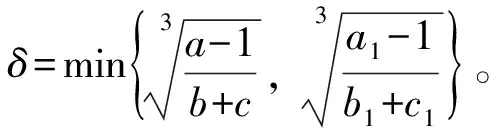
证明：利用第二数学归纳法证明该结论。

假设命题中的条件成立，则当n=0时，由系统(1)可得

(2)

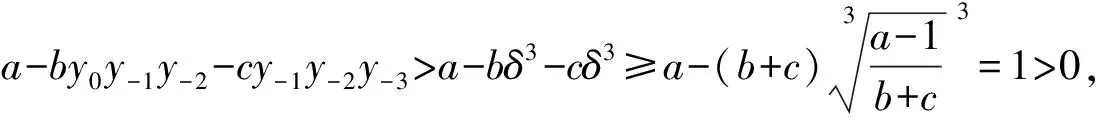
根据式(2)，可得0

现在设n≤p(n,p∈+)时结论成立，即当n≤p时，有0

(3)

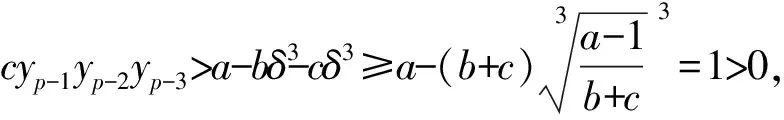
进而由式(3)，可得0

由数学归纳法可知该定理结论成立。定理1得证。

定理2 若定理1的条件成立，则系统(1)以(xi,yi)(i=-3,-2,-1, 0)为初值的解序列{(xn,yn)}都有界且收敛于(0,0)。

证明：设{(xn,yn)}为系统(1)以(xi,yi)(i=-3,-2,-1,0)为初值的解序列。由定理1的证明过程，可得

x-1>x1>x3>x5>…>0,

x0>x2>x4>x6>…>0,

y-1>y1>y3>y5>…>0,

y0>y2>y4>y6>…>0。

记M0=max{x-1,x0,y-1,y0}，从而有

M0≥x-1>x1>x3>x5>…>0,

M0≥x0>x2>x4>x6>…>0,

M0≥y-1>y1>y3>y5>…>0,

M0≥y-1>y1>y3>y5>…>0。

由此可知，

进一步有

当n=2p时，有

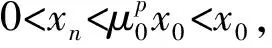
当n=2p+1时，有

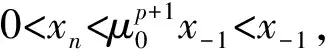
2 平衡点的存在性与稳定性分析

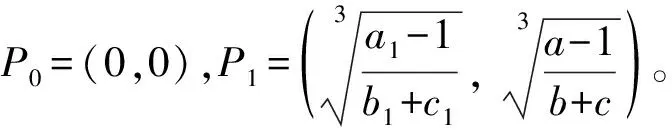
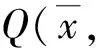
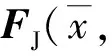
其中：

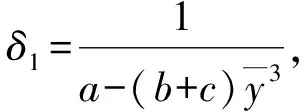
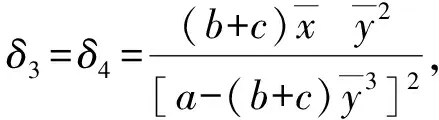
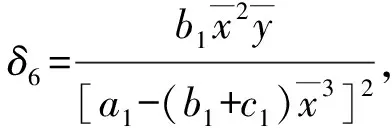
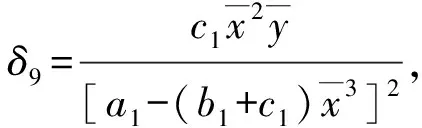
引理1[11]考虑差分系统

Xn+1=F(Xn),n=0,1,2,…,

(4)

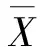
P(λ)=l0λn+l1λn-1+…+ln-1λ+ln,

(5)

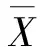
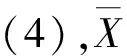
定理3 系统(1)存在平凡平衡点P0=(0, 0)，并且如果a>1,a1>1，则该平衡点是局部渐近稳定的。

证明：系统(1)存在平凡平衡点P0=(0,0)，且系统(1)在点P0处的线性近似系统为

Xn+1=FJ(P0)Xn，

其中

Xn=(xn,xn-1,xn-2,xn-3,yn,yn-1,yn-2,yn-3)T，

FJ(P0)的特征多项式为

P(λ)=|λE-FJ(P0)|=

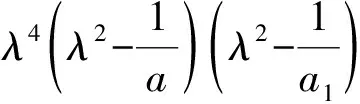
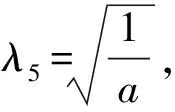
定理3得证。

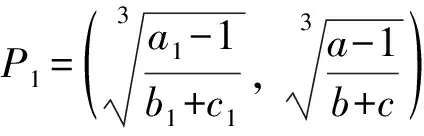
证明：系统(1)关于正平衡点P1的线性近似系统为

Xn+1=FJ(P1)Xn,

求得

FJ(P1)=

其中

由于a>1，a1>1，因此M,M1>0。

矩阵FJ(P1)的特征多项式为

P(λ)=|λE-FJ(P1)|=

化简得

P(λ)=λ8-(M+M1+2)λ6-[M(M1+N1)+

M1(M+N)]λ5+[1-M(M1+N1)-

M1(M+N)-(M+N)(M1+N1)]λ4+

[(2(M+N)(M1+N1)+MN1+M1N]λ3+

[(M+N)(M1+N1)+N1(M+N)+

N(M1+N1)]λ2+[N1(M+N)+

N(M1+N1)]λ-NN1。

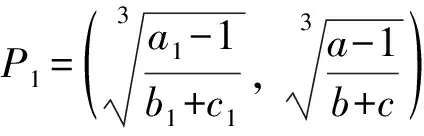
定理4得证。

3 系统(1)解收敛到平衡点的收敛速率分析

Xn+1=[A+B(n)]Xn，

式中：{Xn}(n∈)为m(m∈+)维矢量Xn的序列；A∈Cm×m为常数方阵，Cm×m为m阶常数矩阵集；B(n)∶Z+→Cm×m为矩阵函数且为与向量范数相容的任意一种矩阵范数。

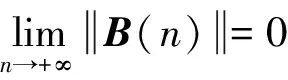
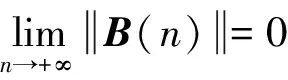
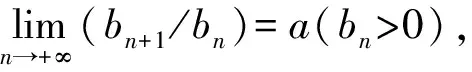
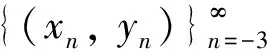
令

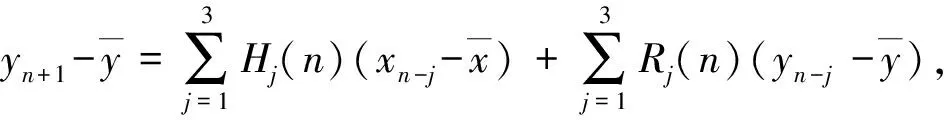
求得

(6)

则式(6)可写为

In+1=T(n)In=

对Kj(n)、Lj(n)、Hj(n)、Rj(n)(j=0,1,2,3)取极限得

这时有

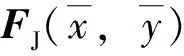
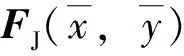
4 系统(1)阶-2周期解的存在性

定理5 1)假设a>1,a1>1, 若b=c和b1=c1至少有一个成立, 则系统(1)存在正的阶-2周期解；

2)若a=1,a1=1中的任意一个成立,则系统(1)存在阶-2周期解。

证明：若系统(1)存在阶-2周期解，则由阶-2周期解的定义可知，存在2个数组(s1,t1)和(s2,t2)，s1=s2与t1=t2不同时成立，并且满足

(7)

这样，系统(1)阶-2周期解的存在性就转化为讨论上述方程组s1=s2与t1=t2不同时成立的解(s1,t1,s2,t2)的存在性。

1)当s1、t1、s2、t2均非零且a>1，a1>1时，式(7)等价于

(8)

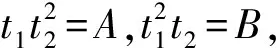
又由于b1=c1，因此，式(8)后2个方程为同一方程b1s1s2(s1+s2)=a1-1，即

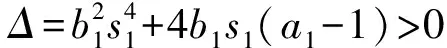
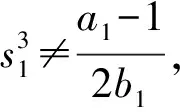
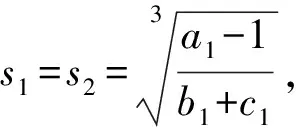
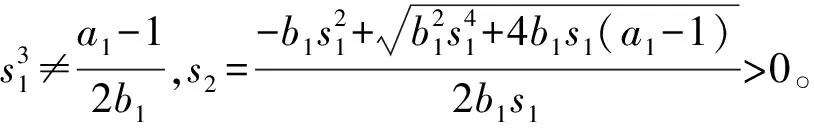
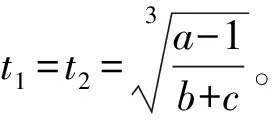
综上所述，假设a>1,a1>1，若b=c和b1=c1至少有一个成立，则系统(1)存在正的阶-2周期解。

2)当a=1时，由式(7)可得，若s1=s2=0，此时只要选取满足t1、t2不全为0的任意实数，且a1=1，则确定的序列(s1,t1),(s2,t2),(s1,t1),(s2,t2),…为系统(1)的阶-2周期解；若s1,s2≠0，则有

t1t2(bt2+ct1)=t1t2(bt1+ct2)=0。

(9)

以下分4种情况进行讨论。

①若t1=0,t2≠0,此时bt2+ct1≠0,bt1+ct2≠0,则s1与s2的取值须满足s1s2(b1s1+c1s2)=a1-1，即

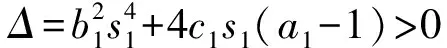
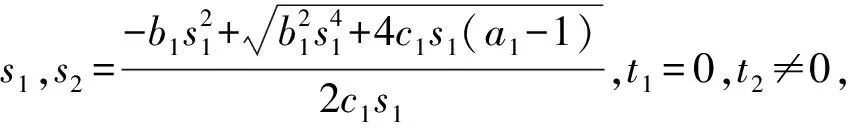
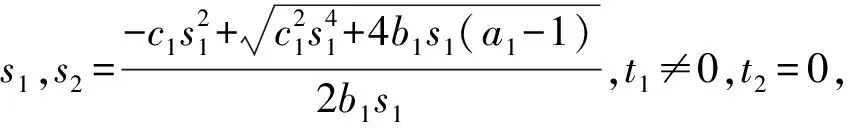
③若t1=0,t2=0，此时bt2+ct1=0,bt1+ct2=0,只要选取满足s1,s2不全为0的任意实数，则确定的序列(s1,t1),(s2,t2),(s1,t1),(s2,t2),…为系统(1)的阶-2周期解。

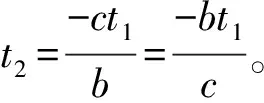
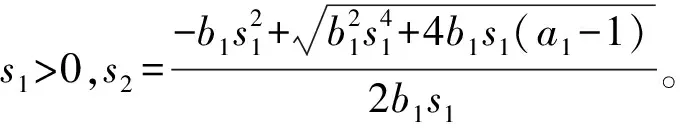
a1=1的情况类似可证。

综上所述，若a=1，a1=1中的任意一个成立，则系统(1)存在阶-2周期解。

定理5得证。

5 数值模拟

利用数值模拟的方法来验证定理2解的收敛性、定理4正平衡点的不稳定性、定理5阶-2周期解的存在性与不唯一性。

例1 在系统(1)中取a=1 126,b=0.008,c=2.1,a1=1 146,b1=2.01,c1=1.7,得到系统

(10)

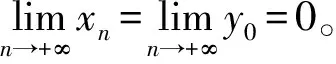
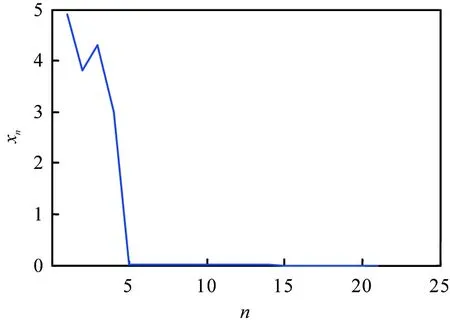
(a) xn随n的变化

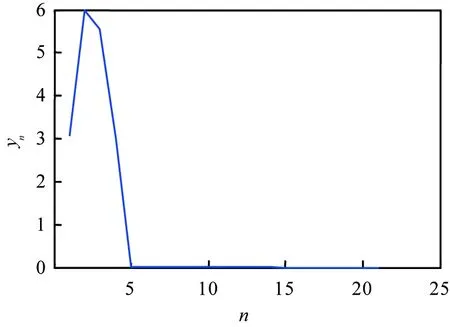
(b) yn随n的变化{(xn, yn)}(n∈)—系统(10)所确定的解序列。图1 系统(10)中xn、yn随n的变化

例2 在系统(1)中a=9,b=0.62,c=0.38,a1=28,b1=0.3,c1=0.7, 得到系统

(11)

容易验证定理4的条件成立，且P(3, 2)为该系统的一个正平衡点，取x-3=3.000 1,x-2=3.000 1,x-1=3.000 1,x0=3.000 1,y-3=2.001,y-2=2.001,y-1=2.001,y0=2.001,利用MATLAB软件分别作出n→xn,n→yn的图像，如图2所示。由图可知，尽管初值与平衡点P相当接近，但是解序列未全留在P的足够小邻域内，即P是不稳定的，这与定理4相符。

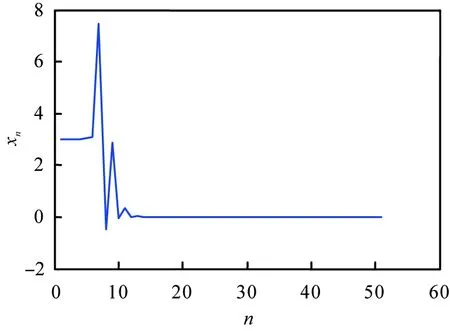
(a) xn随n的变化

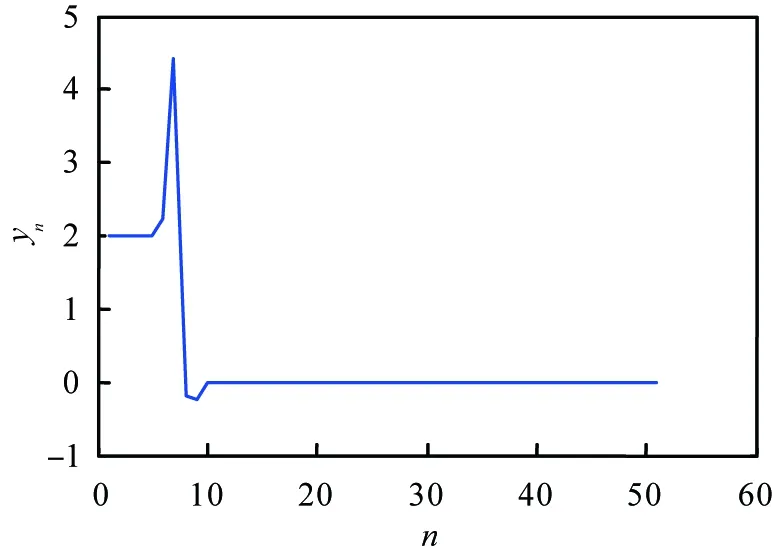
(b) yn随n的变化{(xn, yn)}(n∈)—系统(11)所确定的解序列。图2 系统(11)中xn、yn随n的变化

例3 在系统(1)中a=85,b=1,c=1,a1=7,b1=1,c1=1,得到系统

(12)

容易验证定理5中1)的条件成立。取x-3=1,x-2=2,x-1=1,x0=2,y-3=3,y-2=4,y-1=3,y1=4,利用MATLAB软件分别作出n→xn,n→yn的图像，如图3所示。由图可知，{(1,3),(2,4),(1,3),…}为系统(12)的一个阶-2周期解。再取a=10,b=0.5,c=0.5,a1=1,b1=0.3,c1=0.7,得到系统

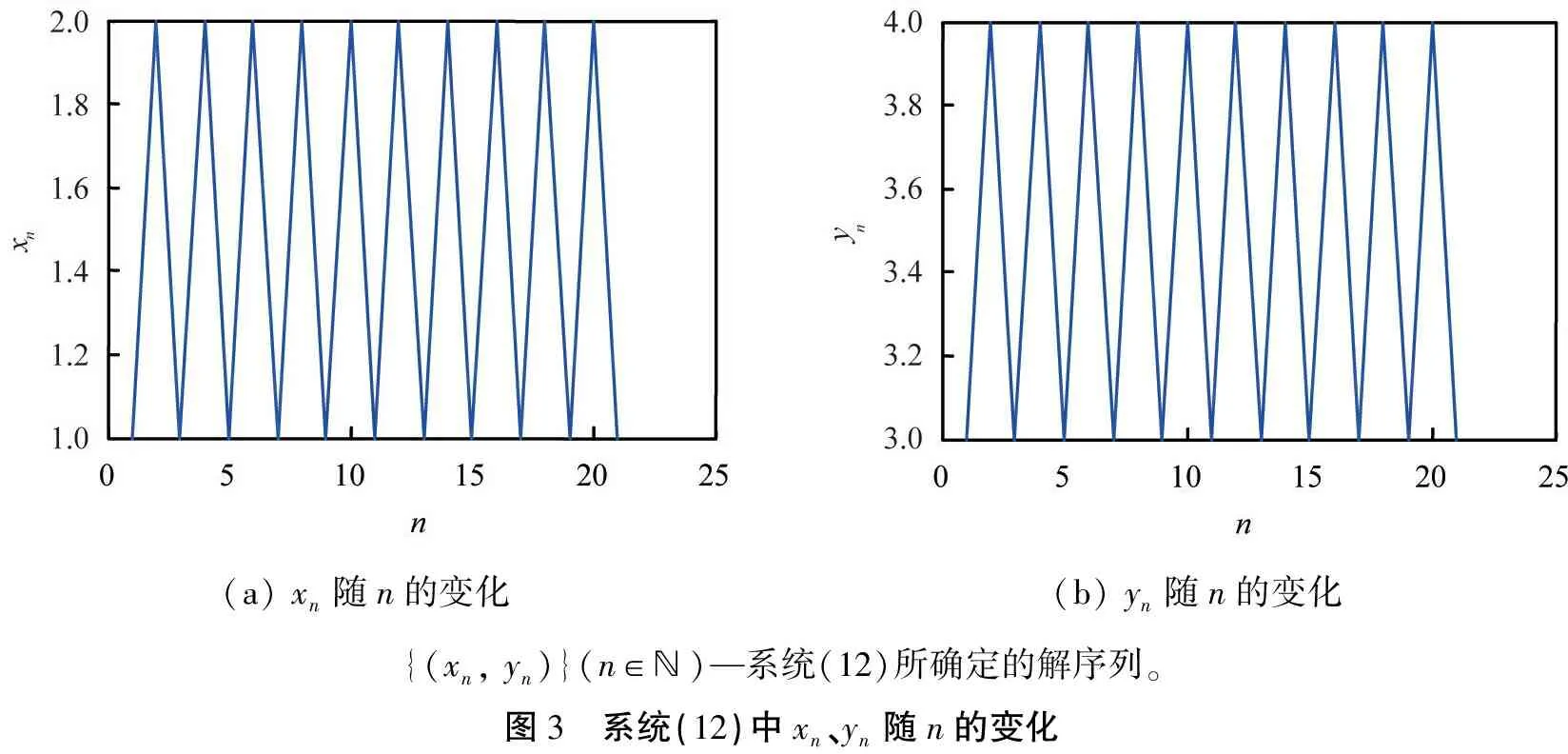
(a) xn随n的变化(b) yn随n的变化{(xn, yn)}(n∈ℕ)—系统(12)所确定的解序列。图3 系统(12)中xn、yn随n的变化

(13)

容易验证定理5中2)的条件成立。取x-3=0,x-2=0,x-1=0,x0=0,y-3=1,y-2=2,y-1=1,y0=2,利用MATLAB软件分别作出n→xn,n→yn的图像，如图4所示。由图可知，{(0,1),(0,2),(0,1),…}为系统(13)的一个阶-2周期解。这与定理5相符。

(a) xn随n的变化(b) yn随n的变化{(xn,yn}(n∈ℕ)—系统(13)所确定的解序列。图4 系统(13)中xn、yn随n的变化

6 结论

本文中讨论了一类特殊的四阶有理差分系统的定性行为。 利用分析的方法证明了在一定条件下正解的存在性与收敛性；利用Hurwitz判据证明了当a>1,a1>1时，平凡平衡点的局部渐近稳定性及正平衡点的不稳定性；利用Poincaré-Perron方法分析了解收敛到平衡点的收敛速率；利用代数方法讨论了当a≥1,a1≥1时，阶-2周期解的存在性与不唯一性；通过数值模拟证明了解的收敛性、正平衡点的不稳定性以及阶-2周期解的存在性与不唯一性的正确性。 该系统的全局行为是下一步要研究的内容。