具有双时滞及Holling II型功能反应捕食模型的Hopf分支

，

(太原理工大学 数学学院，山西 太原 030024)

在种群动力学研究中，时间因素对捕食系统的影响是不容忽视的，并且近年来关于时间对捕食系统的研究已经取得了许多有价值的成果，因此对含时滞项捕食系统的研究很有必要。在捕食模型中，功能反应函数是一个关键性的因素。文献[1-6]中研究了时滞与功能反应函数的捕食者-食饵模型，文献[7]中研究了食饵、捕食者2种群模型，文献[8-10]中对具有延迟的捕食者-猎物系统进行研究，文献[8]中探讨了有时滞项和Holling II型功能反应函数的2种群捕食模型在每个平衡点的稳定性和正平衡点处的Hopf分支。本文中考虑到种群的生物学意义，只对正平衡点处的稳定性和Hopf分支进行研究，探讨双时滞3种群之间的捕食模型的正平衡点的稳定性和Hopf分支的存在性。

1 系统正平衡点的稳定性

基于双时滞和Holling II型反应函数对种群密度的影响，本文中研究以下具有双时滞3种群之间的捕食模型，

(1)

式中：x1(t)、x2(t)、x3(t)分别为时间t处的一级食饵、二级食饵和捕食者这3个物种的种群密度；r1为一级食饵的内禀增长率；r2和r3分别为二级食饵和捕食者的死亡率；a1为一级食饵相互之间的竞争率；a2为二级食饵捕食一级食饵的营养转化率；a3和a4分别为捕食者对二级食饵的捕获率和消化率；m为捕食者的半饱和度；a1、a2、a3、a4、r1、r2、r3、m均为大于0的常数；τ1为追捕时间；τ2为成熟期。 时滞τ1、τ2基于以下假设： 捕食者的变化情况取决于在之前一段时间内食饵和捕食者的数量。 假设x2(t)和x3(t)这2种群有相同的追捕时间τ1和相同的成熟期τ2，根据生态学中种群密度的实际意义，系统(1)定义在三维向量空间+3={(x1,x2,x3)∈3∶x1≥0,x2≥0,x3≥0}上且初值满足条件

x(t)=(x1(t),x2(t),x3(t))∈C+=

{(-τ,0],+3},x1(t),x2(t),x3(t)>0。

其中C+为定义在定义域为(-τ，0]、值域为+3的连续函数的集合，τ为时滞量。

下面讨论系统(1)正平衡点处的稳定性。

定理1 当系统(1)满足条件

(2)

其中

证明：如果系统(1)存在平衡点,则应满足

(3)

解(3)可得每个种群密度均不为0的平衡点只有

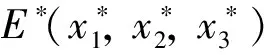
p1=

q=

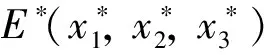
λ3+p1λ2+(p2λ+q)e-λτ。

(4)

根据条件，显然有p1>0,p2>0,q>0。

当τ=0时，特征方程(4)变为

λ3+p1λ2+p2λ+q=0。

(5)

由p1>0,p1p2-q>0，可得

H1∶p1>0，

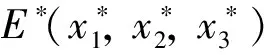
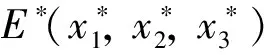
证明：当τ>0时，假设特征方程(4)的一个纯虚根为λ=iω(ω>0)，则ω满足

由两式平方相加可得

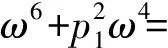
qcosωτ)2。

(6)

整理式(6)可得

即

从而得出ω0所对应的多个τ0,即

根据Bulter[12]引理，得证。定理3证毕。

2 Hopf分支的存在性

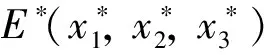
证明：将λ=λ(τ)代入特征方程(4),有

λ(p2λ+q)e-λτ，

则

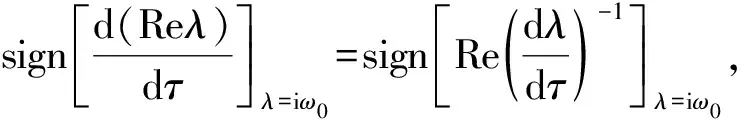
显然

则有

定理4证毕。

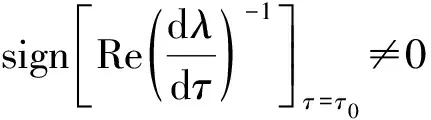
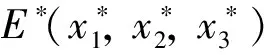
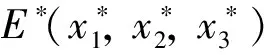
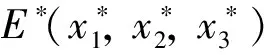
3 数值模拟

下面验证当τ=0(见图1)和τ≠0(见图2、3)时，系统(1)在正平衡点的稳定性,并在分支参数值不同时对系统(1)进行模拟。考虑系统

经计算可得该系统的正平衡点E*(0.65, 1.5, 0.2)，进一步计算可以得出τ0=0.785 4，取τ1=0.3,τ2=0.4时，τ=τ1+τ2=0.7<τ0，则E*(0.65,1.5,0.2)是稳定的平衡点(见图2)；当τ1=0.3,τ2=0.5,即τ=τ1+τ2=0.8>τ0，E*(0.65,1.5,0.2)不具有稳定性，可以产生周期解(见图3)。

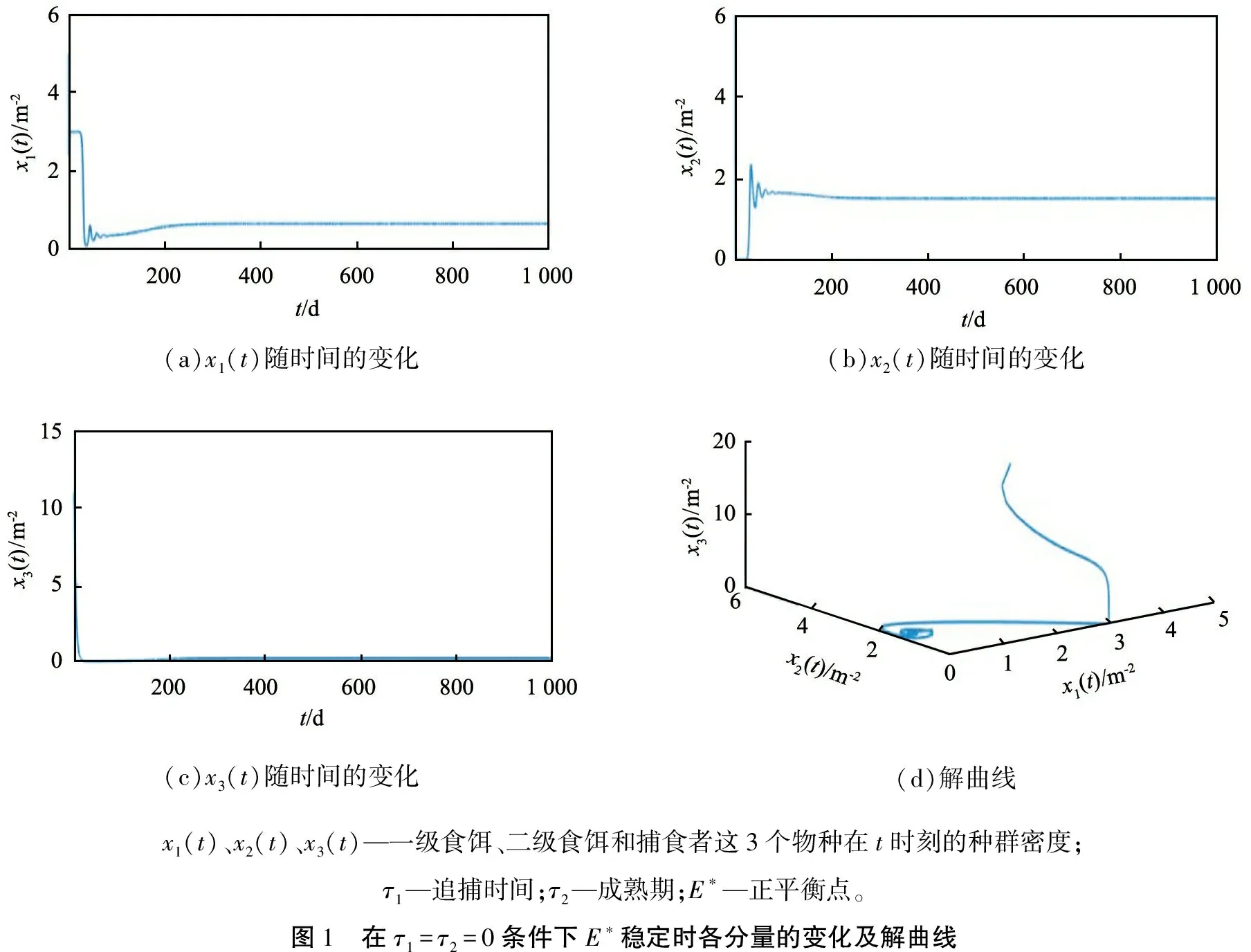
(a)x1(t)随时间的变化(b)x2(t)随时间的变化(c)x3(t)随时间的变化(d)解曲线x1(t)、x2(t)、x3(t)—一级食饵、二级食饵和捕食者这3个物种在t时刻的种群密度;τ1—追捕时间;τ2—成熟期;E∗—正平衡点。图1 在τ1=τ2=0条件下E∗稳定时各分量的变化及解曲线

(a)x1(t)随时间的变化(b)x2(t)随时间的变化(c)x3(t)随时间的变化(d)解曲线x1(t)、x2(t)、x3(t)—一级食饵、二级食饵和捕食者这3个物种在t时刻的种群密度;τ=τ0+τ1—时滞量;τ0—临界滞量;τ1—追捕时间;τ2—成熟期;E∗—正平衡点。图2 在τ=0.7<τ0,τ1=0.3,τ2=0.4条件下E∗稳定时各分量变化及解曲线

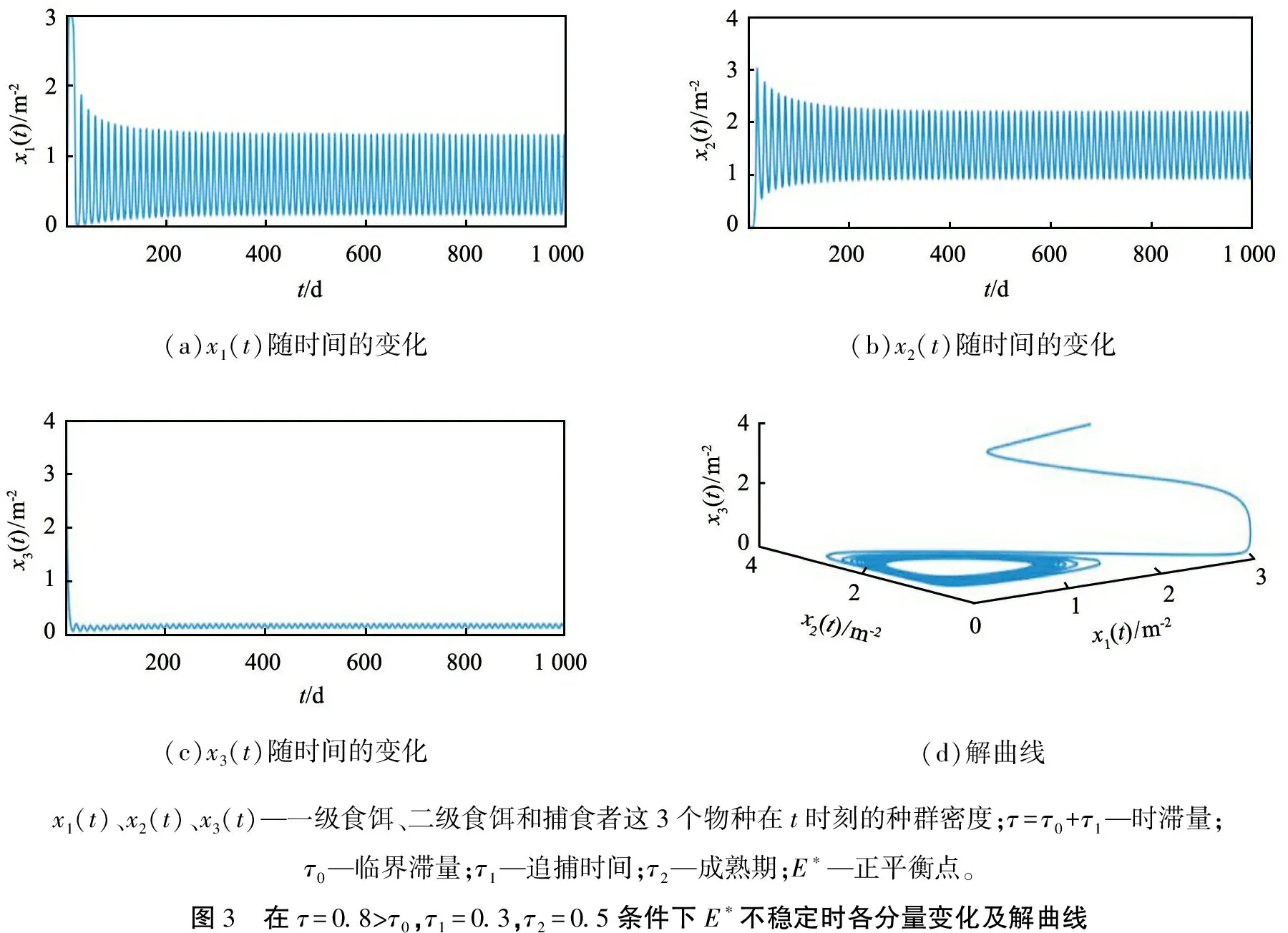
(a)x1(t)随时间的变化(b)x2(t)随时间的变化(c)x3(t)随时间的变化(d)解曲线x1(t)、x2(t)、x3(t)—一级食饵、二级食饵和捕食者这3个物种在t时刻的种群密度;τ=τ0+τ1—时滞量;τ0—临界滞量;τ1—追捕时间;τ2—成熟期;E∗—正平衡点。图3 在τ=0.8>τ0,τ1=0.3,τ2=0.5条件下E∗不稳定时各分量变化及解曲线

4 结论

本文中讨论了一类带Holling II型功能反应的三维捕食系统并且引进了2个时滞项，分析了系统的正平衡点在时滞等于0和不等于0时的稳定性。随着分支数值的增大，系统由稳定变成不稳定，当时滞小于临界值时，系统是稳定的；当时滞大于临界值时，系统是不稳定的，会产生Hopf分支，并产生周期解。在第II类功能反应函数的捕食系统中引入随机项进行进一步讨论是以后的研究方向。