基于改进滑模控制的电网模拟器研究

李修旋，陈国初，张鑫

（上海电机学院电气学院，上海 201306）

0 引言

近年来，随着风能等清洁能源大量的并入电网，电网对变流器的要求越来越高，大量变流器的接入会对电网的稳定性产生影响，实际电网主要目的是保证供电的稳定性，不能产生故障对变流器进行测试，因此，能够模拟电网各种故障的电网模拟器的研制变得越来越重要[1-5]。

因为逆变器自身有开和关的特性，属于变结构系统，因此，滑模控制很适合对逆变器控制[6-9]。但是，从本质上说，滑模变结构是非线性控制，开和关的控制特性，导致其存在抖振的现象，使其在实际的应用中不是很完美。国内和国外的学者提出许多消除抖振的方法[10-13]。文献[14]引进模糊控制，可以对系统的扰动实现实时在线的观测，很大程度上减小切换的增益，大大降低抖振影响。文献[15]使用滑动扇区的方法，扇区内部运用连续等效的控制方法，扇区外部，使用趋近率的控制方法，大大降低了抖振的影响。文献[16]使用能量约束的方法，使得控制器付出很小的代价就能保证系统的运动状态维持在滑模面上，减小了抖振。

本文主要针对滑模控制中的抖振现象，提出双幂次趋近律，使得系统在远离滑模面时速度很快，迅速趋向于滑模面，在滑模面附近时，速度很小，大大减小抖振。从而可以保证电网模拟器能够输出良好的电压波形，大大提高控制系统的稳定性[17-20]。

1 双幂次趋近律

趋近律由我国控制理论学者高为炳提出，常用趋近律一般包括：等速趋近律、指数趋近律、幂次趋近律。等速趋近律的趋近速率单一，运动品质不是很好，目前很少使用这一趋近律；指数趋近律能够有效的改变系统状态的运动品质，但是，由于常数项的存在，不能够完全消除抖振；幂次趋近律可以保证在系统状态接近滑模面时，大大降低速度，从而减小抖振问题的影响，但是，在初始的状态和滑模面相距比较远的时候，趋近的速率会过于缓慢。为了解决上面问题，本文提出一种双幂次趋近律：

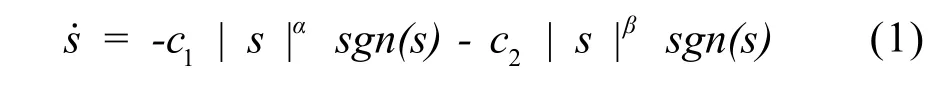
其中：0＜ α ＜1， β ＞1，c1＞0，c2＞0。

假设滑模控制系统的初始状态s(0)＞1，则可以分两段计算趋近律的收敛时间。

第一阶段：s(0)→s=1，由于0＜α＜1，β＞1，所以式(1)中的第二项起主导作用，其作用远大于第一项，因此能够忽略第一项的影响，式(1)可以变为：

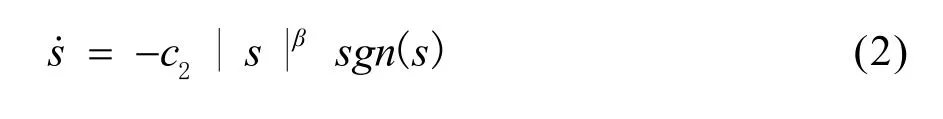
对式(2)两边进行积分，可以得到这一阶段所需的时间为：

第二阶段：s=1→s=0，由于0＜α＜1，β＞1，所以式(1)中的第一项起主导作用，其作用远大于第二项，因此能够忽略第二项的影响，式(1)可以变为：

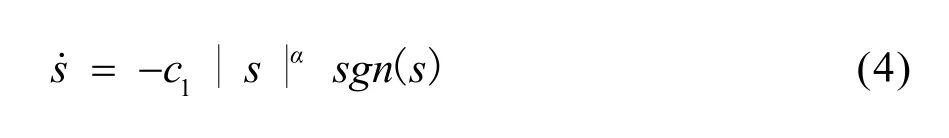
对式(4)两边进行积分，可以得到这一阶段所需的时间为：

因此，可以得到整个过程的收敛时间，即

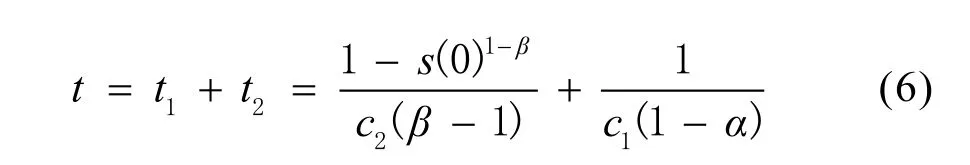
同理，能够很容易的证明在s(0)＜−1时，收敛的时间和式(6)一样。

为比较不同趋近律的趋近速度，下图给出了三种趋近律的趋近曲线，选取相同的控制器参数，其s随时间t的收敛情况如图1所示。

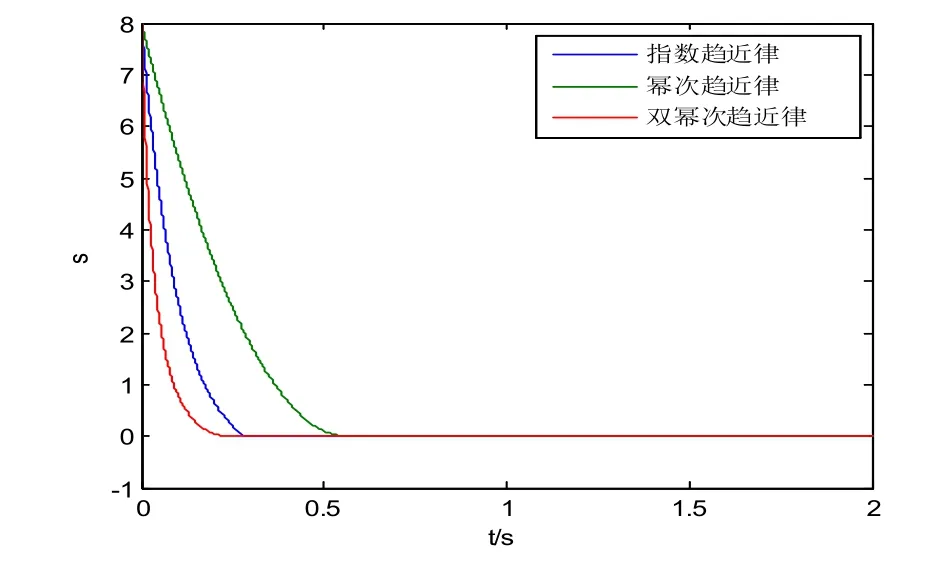
图1 不同趋近律的s变化曲线Fig.1 Change curve of s with different law of approach

从图1得出，初始状态接近滑模面过程中，双幂次趋近律的趋近速度高于指数和幂次趋近率；在指数趋近律接近滑模面时，趋近速度突然减小，在双幂次趋近律接近滑模面时，趋近速度平滑减小。因此，双幂次趋近律不仅可以保证远离滑模面的快速性，同时具有靠近滑模面的平滑性。双幂次趋近律的性能好于指数和幂次趋近律。

2 电网模拟器拓扑结构的选择

本文采用了一种比较新颖的电网模拟器的拓扑结构，如图2所示，该拓扑结构由一个三相全桥整流器、三个单相全桥逆变器和三个LC滤波器组成。

整流环节：电网模拟器的测试对象为有源负载，要能够模拟能量回馈，因此需要实现四象限运行。但是，单相PWM整流的输出会产生二次谐波，会对系统稳定性产生影响，因此，本文选用直流侧电压相对平稳的三相PWM整流。

逆变环节：三相PWM逆变器的输出，不能够准确模拟不平衡电压零序分量的情况，所以，本文使用三个单相的全桥逆变器，分别模拟三相电压的一相，可以实现单相电压的自由跌落，模拟出不同种类的故障。

图2 电网模拟器拓扑结构Fig.2 Topology structure of grid simulator

3 逆变器滑模变结构控制器设计

3.1 单相全桥逆变器的数学模型

本文主要对逆变侧进行研究，电网模拟器的逆变环节采用三个单相全桥逆变器，为了方便起见，本文只对单相全桥逆变器进行研究，其电路结构如图3所示。

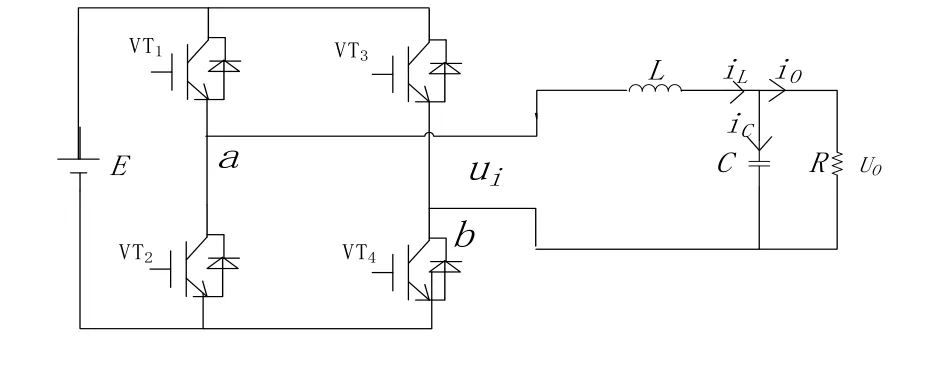
图3 单项全桥逆变器Fig.3 Single-item full-bridge inverter

其中，VT1-VT4是ΙGBT，E为直流母线端电压，L、C分别为滤波器的电感和电容，ui为输出端电压， iL、iC、iO分别为电感、电容和输出的电流，uO为输出电压。

由于单相全桥逆变器的输出电容电压和其导数能够持续可测，因此，选取电容电压和其导数作为系统状态变量，可得系统状态方程：

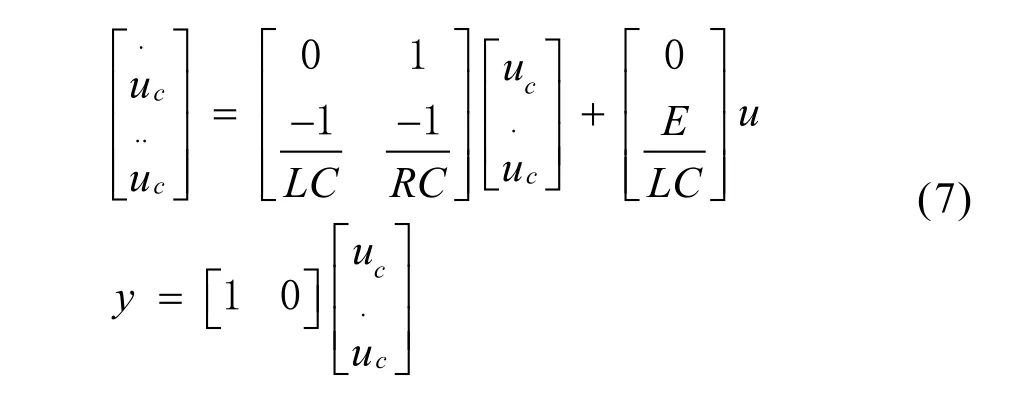
其中， u= {− 1 ,1}，代表逆变器开关管的通和断两种状态。u=1时，VT1和VT4导通，uin=E；u=−1 时，VT2和VT3导通，uin=−E。

3.2 滑模控制器的设计

逆变器的滑模控制框图，如下图所示，其中，Go是逆变器对应的传递函数。

图4 单相逆变器滑模控制框图Fig.4 Sliding mode control block diagram of single-phase inverter

滑模控制器设计可分为两部分：滑模面的选取和趋近律的设计。

由于电容电压和电容电流能够使用电压和电流传感器通过取样的方式得到，因此，只要参考信号已知，就可以选用参考信号和状态变量之差，作为式(7)中新的状态变量，系统新的状态方程可以变为：

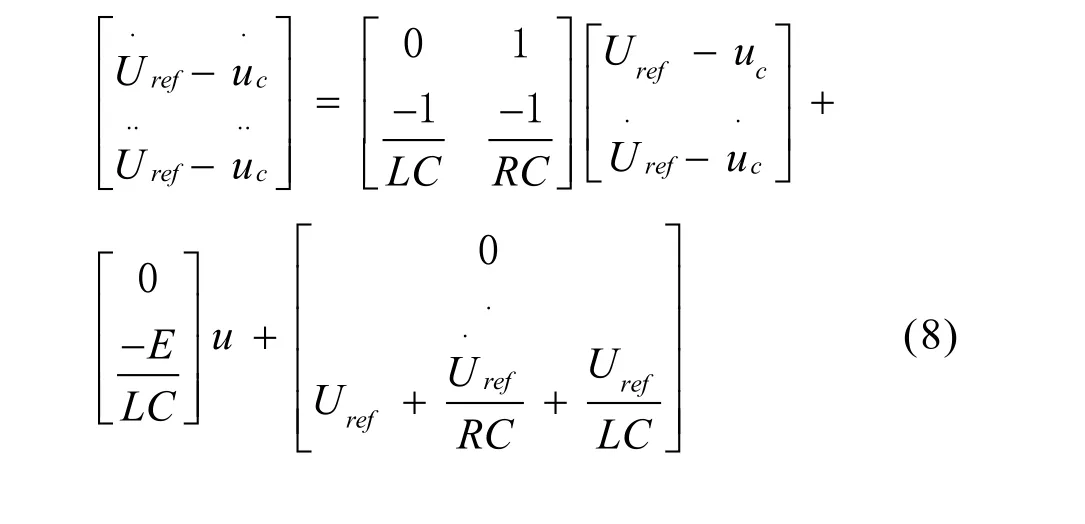
要实现滑模控制，滑模面的设计是必不可少的，本文在式(8)确定的状态平均空间平面上，选取一条斜率为负的过原点的直线作为滑模面函数，如式(9)所示。

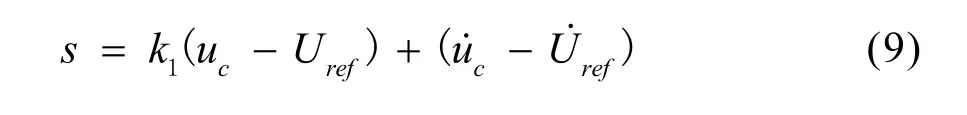
其中，为了保证系统大的状态轨迹能够沿着滑模面滑动，最终稳定于原点，因此取k1＞0。

由上文分析可知，本文选取双幂次趋近律对滑模控制器进行设计，由式(1)、式(7)和式(9)可得，基于双幂次趋近律的滑模控制器为：

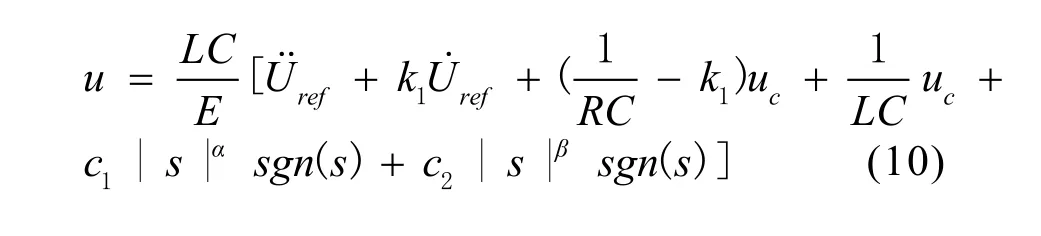
为了保证设计控制器的正确性，需对系统的稳定性进行证明，选取李雅普诺夫函数为：

式中， v(t)为李雅普诺夫函数；t为时间。

由上式得，系统渐近稳定，本文设计的趋近律满足系统稳定性要求。

4 基于SimuLink的仿真实验

本文将使用MATLAB 2013b中的SimuLink和SimPowerSystems，选取其中的模块搭建仿真模型，并对其进行仿真，验证改进的滑模控制器得有效性。

仿真中选取得参数如下：L=5 mH， C =20 uF ，R=10 Ω，fK=10 kHz，fS=50 Hz，Udc=540 V，基波有效值220 V。图5和图6分别给出逆变器以及改进滑模控制器的仿真模型。

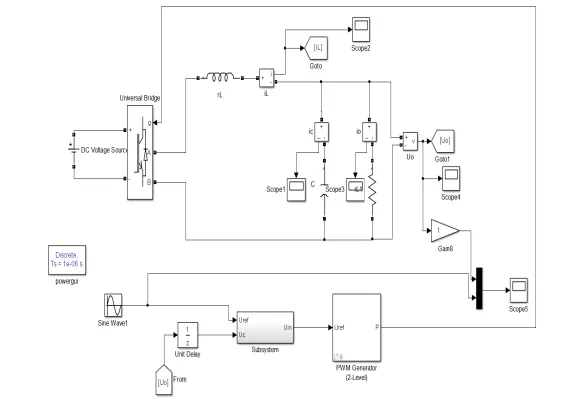
图5 改进滑模控制的控制电路仿真图Fig.5 Simulation diagram of control circuit of improved sliding mode control

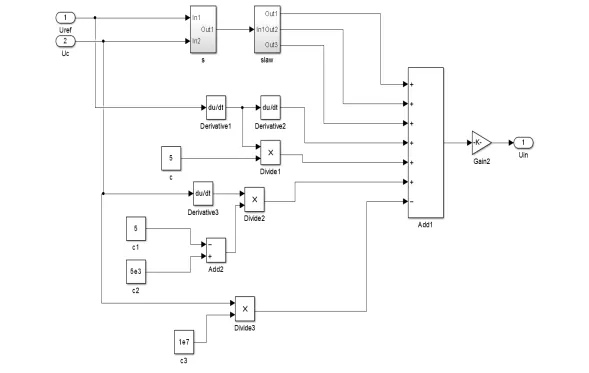
图6 改进滑模控制系统仿真Fig.6 Improved sliding mode control system simulation

设置电压在0.055 s时跌落到其额定值的30%，通过SimuLink仿真可以得到滑模控制和改进的滑模控制这两种控制策略的输出电压的波形图，以及其输出电压波形对应的FFT分析图，如图7～10所示。

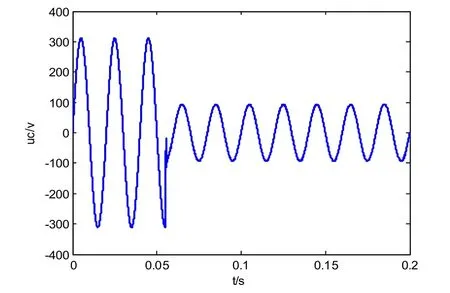
图7 滑模控制输出电压对给定电压的跟踪Fig.7 Tracking of output voltage by sliding mode control to a given voltage

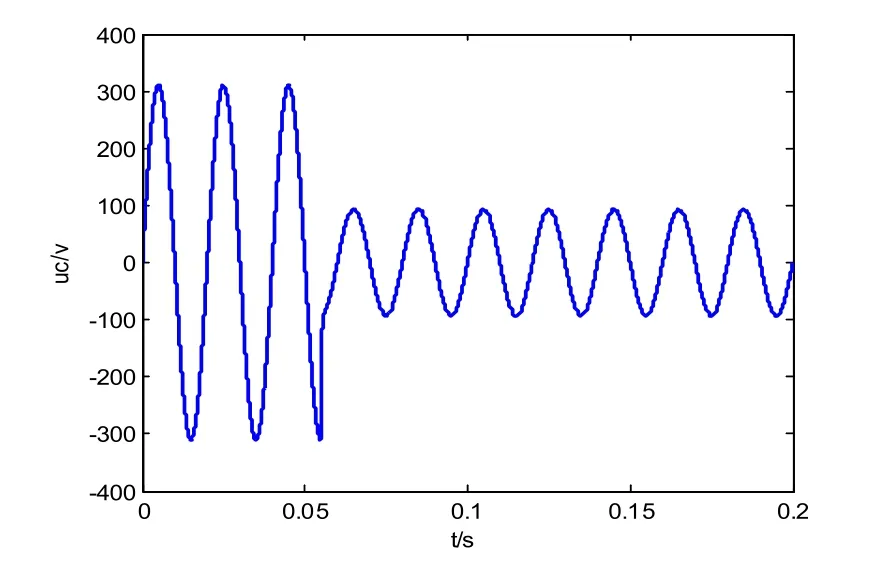
图8 改进滑模控制输出电压对给定电压的跟踪Fig.8 Improved tracking of output voltage of sliding mode control on given voltage

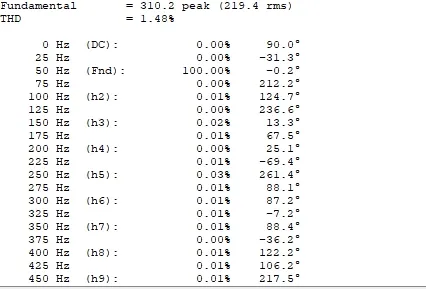
图9 滑模控制输出电压的FFT分析Fig.9 FFT analysis of output voltage controlled by sliding mode

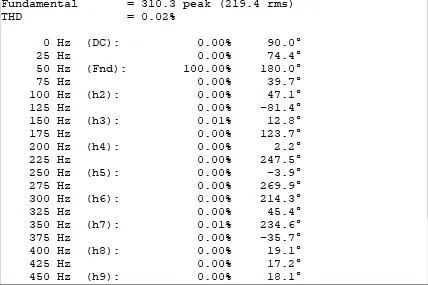
图10 改进滑模控制输出电压的FFT分析Fig.10 FFT analysis of improved slidemode control output voltage

从图7和图8能够看出，在0.055 s以前，输出电压波形基本一致，说明滑模控制以及改进的滑模控制，都可以很好的追踪给定的电压波形，在时间为0.055 s时，电压突然跌落到给定电压值的30%，滑模控制能够较迅速的跟踪到给定电压波形，但跌落瞬间会产生较大的抖振，而改进的滑模控制不仅能够迅速跟踪跳变的电压，而且产生的抖振几乎为零。图9以及图10是对两种控制的电压波形进行FFT分析，可得改进滑模控制得THD比滑模控制的THD小很多。综上所述，改进滑模控制能够极大程度消除抖振，更好的对给定电压波形进行跟踪。

5 实验验证

根据上文分析和研究，搭建一台10 ΚW级的电网模拟器综合实验平台，如图11所示；从图12能够看出，采用上述改进滑模控制的电网模拟器能够准确模拟出单相电压跌落，并且对跌落电压能够实现准确跟踪；从图13可以看出，电网模拟器可以模拟出正常三相电压。改进滑模控制的有效性得以验证。

图11 电网模拟器实验平台Fig.11 Experimental platform of grid simulator

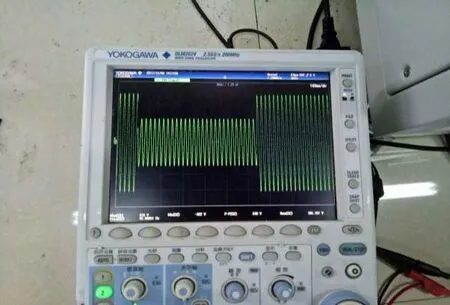
图12 单相电压跌落波形Fig.12 Single-phase voltage drop waveform

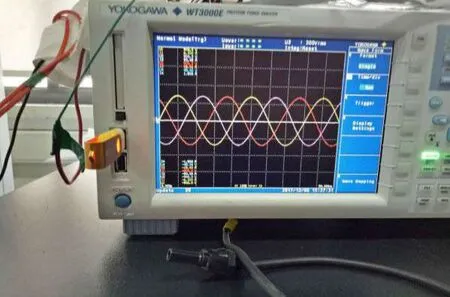
图13 三相电压波形Fig.13 Three-phase voltage waveform

6 结论

本文首先对滑模控制的趋近律进行了分析，为了解决滑模控制存在的抖振问题，提出了双幂次趋近律，并对其进行仿真验正；然后，提出电网模拟器拓扑结构；再次，建立单相全桥逆变器的数学建模，设计了基于趋近律的滑模控制器；最后，对滑模控制以及改进的滑模控制进行SimuLink的仿真，实验结果表明改进滑模控制能够在很大程度上减小抖振的影响，并基于dSPACE搭建了实验平台，进一步地验证了文中所提改进滑模控制的正确性。