基于SMO的PMSG无位置传感器控制研究

漆文睿，刘军

（上海电机学院电气学院，上海 201306）

0 引言

在使用永磁同步发电机作为交流电源输入的发电系统中，三相永磁同步发电机在原动机的拖动下感应反电势，三相交流反电势作为整流器的输入，经过PWM整流、滤波后给直流负载供电，或经过DC-DC变换器、DC-AC变换器再向负载供电[1-2]。系统结构框图如图1所示：

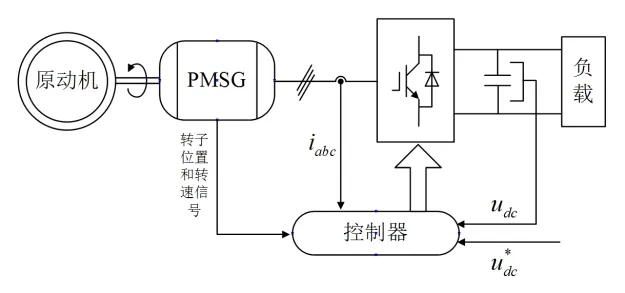
图1 PMSG-PWM整流发电系统结构框图Fig1.PMSG-PWM rectifier power system structure diagram

在上述的PMSG-PWM整流系统中常用SVPWM方式，该方法的实现需要进行坐标变换，即需要获取准确的电机转子位置角信息，永磁同步电动机的高性能控制也离不开准确的转子位置。常用的位置传感器有光电编码器、旋转变压器和霍尔传感器等，然而传感器的使用也会带来安装精度要求较高、维护工作量大、加大电机体积和重量、成本上升、容易受干扰等一系列问题，这在一些条件恶劣的场合会对整个系统的性能造成比较大的影响。因此，对于永磁电机无传感器位置检测的研究十分重要，近年来学者们对无传感器控制有广泛的研究。无位置传感器技术的主要思想是提取电机绕组中的某个电信号估算出转子位置和转速[3-5]，具有代表性的方法有模型参考自适应法、基于各种观测器的方法、基于高频信号注入的方法以及与智能控制理论相结合的方法等，其中利用反电势或者定子磁链估计反电势的方法实时检测定子电压电流估算转子位置，这一类算法主要包括滑模观测器（Sliding Mode Observer, SMO）算法、模型参考自适应（Model Reference Adaptive System, MARS）算法[6-7]、扩展卡尔曼滤波器（Extended Κalman Filter, EΚF）算法[8-9]等。

基于滑模观测器的估算方法鲁棒性好，对参数变化和扰动不敏感，其实质是系统状态的重构。滑模观测器引入了滑模变结构控制的思想，可以通过控制对象的切换将每个结构的优势最大限度的发挥出来，提高系统的整体性能。此外，由于滑模抖振的存在，学者们对滑模观测器的研究主要集中在削抖等方面。文献[10]提出一种自适应滑模观测器并建立自适应律，克服了对电机参数的依赖性；文献[11]提出了基于扩展反电势的模型参考自适应估算方法估算转子位置和转速并进行了实验验证；由于滑模控制存在着高频抖振，反电势的估算结果也同时存在高频抖振的现象，文献[12]采用饱和函数代替符号函数作为切换函数并采用可变截止频率的低通滤波器，有效削弱了抖振；文献[13]将滑模观测器与锁相环技术结合，有效地提高了估算精度。文献[14]从同步旋转坐标系下的永磁电机数学模型出发，设计并实现了滑模观测器方法对转子位置和转速的估计。针对滑模观测器削弱抖振和提高估算精度的目标，本文从同步旋转坐标系下的电机模型出发，采用滑模观测器方法估算PMSG-PWM整流系统的控制算法中所需的转子位置和转速信息，结合PLL锁相环技术，搭建MATLAB仿真验证模型，对比几种滑模切换函数作用下的估算效果。

1 转子位置的滑模观测器估算方法

由永磁同步发电机电机在d-q轴下的数学模型，将定子电流的方程表述如下：

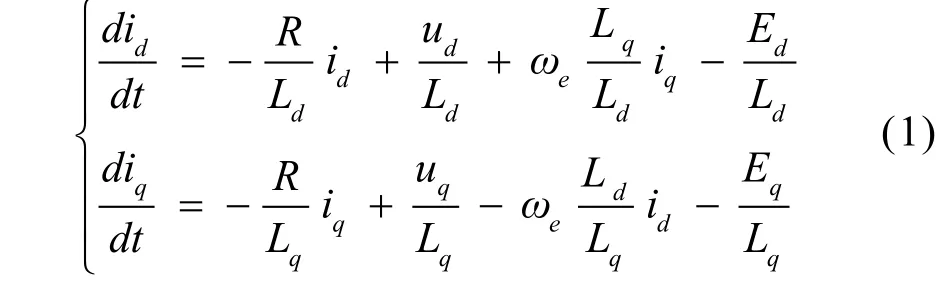
式中：

R——定子电阻；

ωe—— 电角速度；

Ed、Eq——感应电动势的d、q轴分量，其中 Ed= 0，Eq=ωeψf，ψf为转子永磁体磁链。

可将式（1）改写成矩阵形式为：

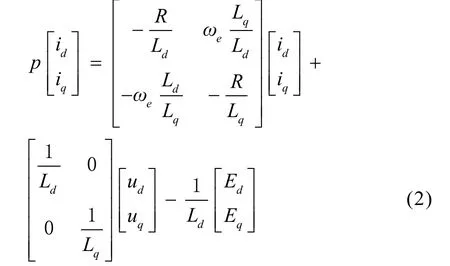
由于Eq中含有ωe项，为获得转速信息，可构建滑模观测器，传统方式[12]使用符号函数作为切换函数，对应的滑模观测器方程为：

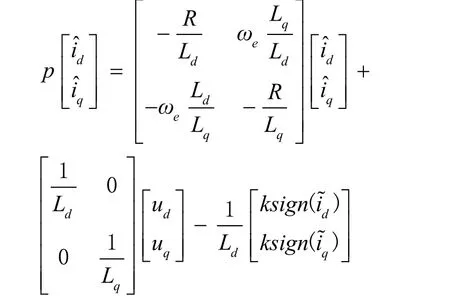
式中，

p——微分算子；

k——滑模增益；

sign(s)——符号函数。

电机处于稳态运行时存在抖振现象，为削弱抖振、减小稳态和动态时的转子位置估计误差，有文献使用饱和函数sat(s)代替符号函数sign(s)。为进一步提高估算准确度，用光滑连续的S型生长曲线 sigmoid(s)函数代替符号函数sign(s)作为切换函数。 sigmoid(s)的表达式为：

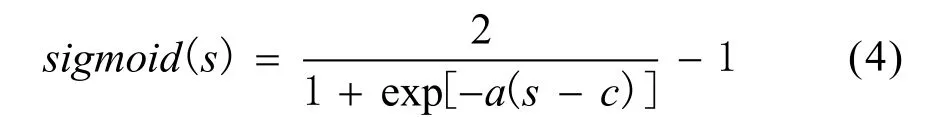
式中:

a——函数斜率，a＞0，a越大曲线约光滑，抖振越小；

c——一般取0。

函数曲线如图2所示：

因此改写式（3）得：

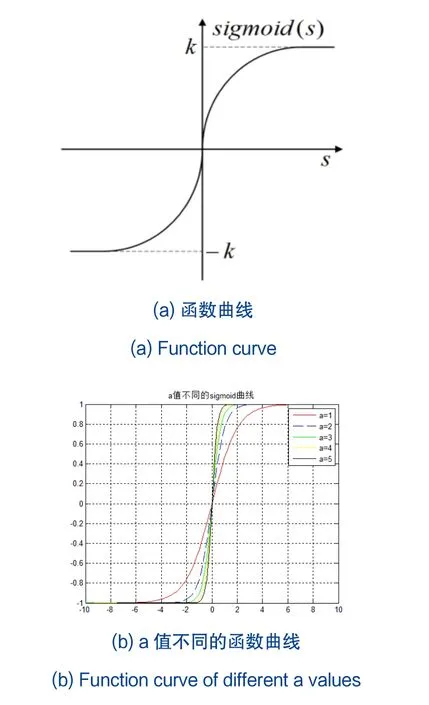
图2 Sigmoid(s)函数Fig.2 Sigmoid(s) function

将式（5）与式（2）作差，得：

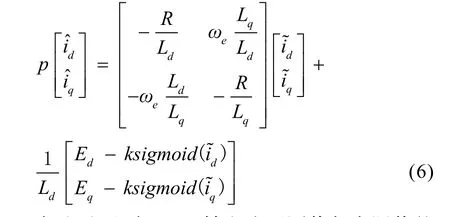
式（6）即为d、q轴电流观测值与实际值的误差方程，将滑模面定义为：利用李雅普诺夫函数易证滑模观测器的稳定性。滑模到达条件为，满足此条件式时运动轨线将于有限时间到达切换面，此时有代入式（6）可得：

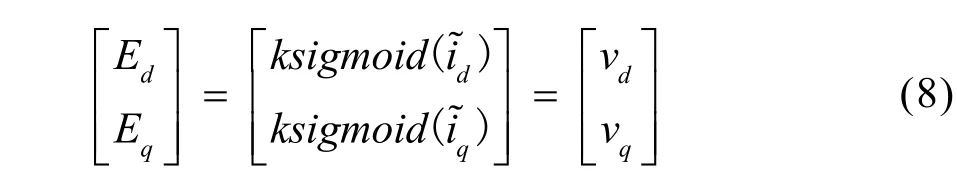
发电机的三相机端电压从三相静止坐标系变换到同步旋转坐标系下d轴电压分量vd为0，因此可构建闭环PΙ控制器，当输出结果与实际值误差为零时可认为输出值即为转子位置实际值。因此为了提高系统转子位置估计的准确性，将锁相环应用于同步旋转坐标系下的滑模观测器来估算转子位置，原理框图如图3所示：

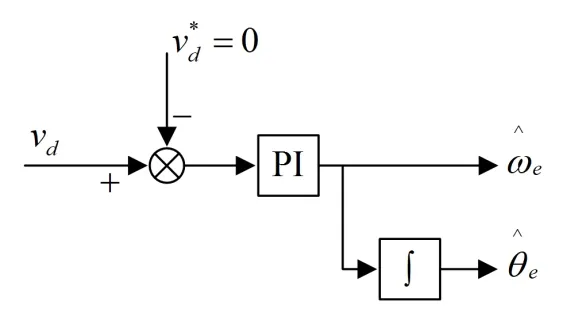
图3 锁相环实现框图Fig.3 PLL implementation diagram

2 建模与仿真

前述同步旋转坐标系下构造的滑模观测器采用连续函数 sigmoid(s)作为切换函数，且结合了锁相环技术。为单独验证该转子位置估计方法对PMSG转子位置的估算效果，将PMSG运行于电动状态，采用基本的的矢量控制策略搭建MATLAB/simulink仿真模型[15]，控制框图如图4所示。

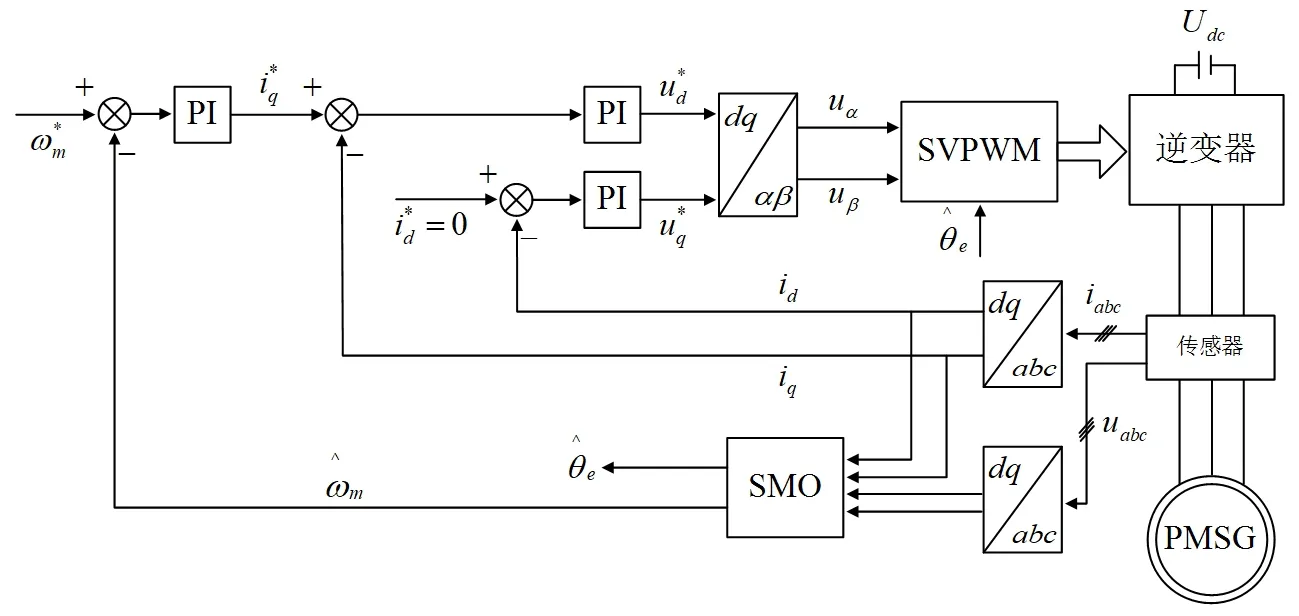
图4 控制系统框图Fig.4 Control system diagram

在图4中，传感器采集PMSG的三相静止坐标系下的三相电压和电流，从三相静止坐标系变换到同步旋转坐标系，id、iq、ud、uq为滑模观测器的输入，滑模观测器输出的转子位置估算值用来实现SVPWM和坐标变换，转速估计值用来实现转速外环。

分别对采用sign(s)、sat(s)和 sigmoid(s)结合PLL锁相环的三种滑模观测器作仿真，仿真参数设置如下：电机极对数 pn= 3；定子电阻R= 0.02Ω ；磁链 ψf= 0.082 Wb；d、q轴电感参数分别为 Ld= 1.54 mH、Lq= 1.12 mH ；直流侧电压 Udc= 311 V；开关频率为10 kHz；仿真时间为0.5 s；转速给定为600 r/min，PMSG运行于空载状态。

转子位置的仿真结果如图5至图7所示。

图5为使用符号函数作为切换函数并结合锁相环估计PMSG转子位置的仿真结果，由图可以看出估计误差抖振现象比较明显，且转子位置估计误差相对较大。

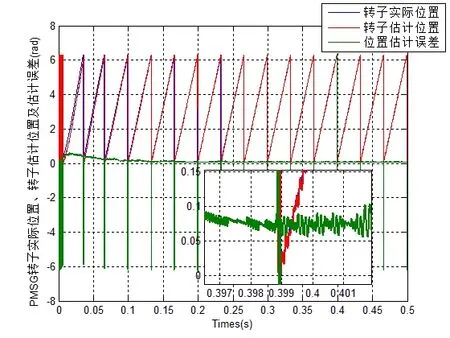
图5 基于符号函数的仿真结果Fig.5 Simulation results based on symbolic function

图6 是采用饱和函数的仿真结果，对比图5可知，抖振现象明显减小，估计误差也进一步降低。

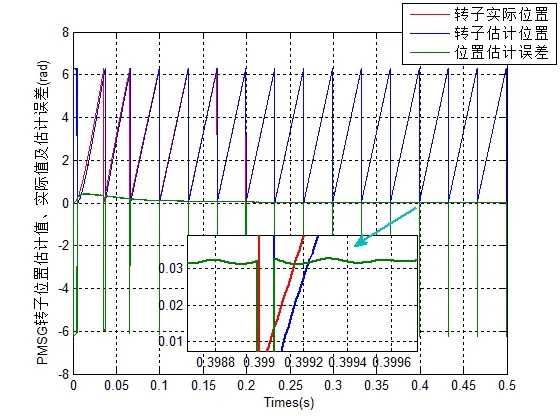
图6 基于饱和函数的仿真结果Fig.6 Simulation results based on saturation function

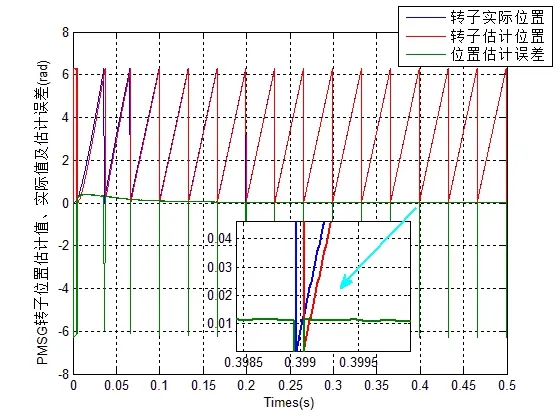
图7 基于连续函数的仿真结果Fig.7 Simulation results based on continuous function

由图7可知，使用 sigmoid(s)作为切换函数在图6的基础上有进一步优化，最终的转子位置角度估算误差小于1°。

以上仿真结果表明，三种切换函数与锁相环技术结合，均可较好的估算转子位置角，其中以光滑连续的 sigmoid(s)函数作为切换函数时效果最好。

3 结论

对于PMSG-PWM整流系统中永磁同步发电机的无位置传感器方法，本文分析了在旋转坐标系下滑模观测器的推导，并结合锁相环搭建了运行于电动状态的PMSG仿真模型，本文用光滑连续函数取代了传统滑模观测器中的符号函数或饱和函数，从仿真结果来看，该方法能更有效的估算转子位置角度，为后续SVPWM整流系统的设计与控制提供了理论基础。