基于Stackelberg微分博弈的北京自住房价格规制模型

陈俊华，吕林峰

（1.中央财经大学 管理科学与工程学院，北京100087；2.杜兰大学 商学院，美国 路易斯安那州 新奥尔良市 70118）

0 引言

2013年10月24日，北京市住房与城乡建设委员会颁布了《关于加快中低价位自住型改善型商品住房建设的意见》（下文称《意见》），首次在全国范围内提出“自住型商品住房”概念。近几年，在北京市房价明显快速上涨的背景下，自住房以较低的价格获得公众的关注。

自住房政策体系的核心是定价机制。通过价格限制或者提供货币补贴来解决社会低收入阶层的住房问题是许多国家通行的做法[1]。Raess等（2002）[2]的研究发现政府对住房租赁价格的管制可能会降低市场租金的长期均衡点，最终实现社会福利提升的效果。但Smith（1998）[3]认为政府的公共住房价格管制政策只能提供少量的公共住房资源给最需要的社会群体，对总体住房状况并不能起到实质性的作用，只能政府的“形象工程”。国内的李晓鹄（2014）[4]研究认为加快中低价位的自住房建设,可以满足中低收入家庭的住房刚性需求，能够部分平抑商品房价格的过快上涨；但同时也可能导致普通住房刚需产品的供给减少,不利于商品房市场的稳定。但有学者董丽丽（2015）[5]指出现行的自住型商品房存在选址偏远、平抑房价作用有限等问题。现阶段自住房的定价机制相对缺乏弹性，政府在《意见》中要求自住房“比同地段、同品质的商品住房价格低30%左右”，这一相对硬性的定价机制对市场的供求关系变动缺乏必要的弹性，对自住房供应中各方博弈主体（政府、房地产开发商和购房消费者等）的经济行为缺乏理性的博弈分析。

本文尝试运用Stackelberg微分博弈模型，模拟自住房定价参与主体各方的经济行为，旨在研究自住房的合理定价机制，通过博弈的方法演绎自住房定价过程及机制的合理性。

1 自住房定价机制研究设计

微分博弈模型是在Cournot模型的基础上，由Stackelberg于1934年提出的[6]。该模型是基于双寡头垄断时的动态博弈模拟，由领导者首先发起行动，之后追随者行动，由于该模型能够模拟交易双方的动态博弈过程，可以较真实地反映市场条件下买卖双方相互作用并最终在商品价格上达到均衡的结果，因此微分博弈模型常常被用于商品定价分析[7]。

在自住房的定价过程中，由于政府可以通过制定价格规制政策来抑制开发商抬高房价的倾向，政府和开发商可以被视为博弈的对手方。政府的政策具有强制性，因此可以假设整个动态博弈过程中的主导者是政府，开发商则是博弈过程中的追随者，其通过积极应对政府制定的政策，来实现自身利益的最大化。本文尝试构建Stackelberg微分博弈模型，深入模拟和分析政府和房地产开发商各自的最优策略，并尝试推导自住房最优定价的数学表达式。

建立Stackelberg微分博弈模型需要具备一些前提条件：

（1）在自住房定价博弈过程中，政府是博弈的领导者，首先发起行动，即其处于博弈的第一阶段，其博弈空间是决定自住房的补偿支付（或税收量），其目的是使得社会福利最大化。

（2）在此博弈过程中，房地产开发商是博弈的追随者，处于博弈过程的第二阶段，其博弈空间是自住房的供应量。本文将开发商视为理性的经济人，即其开发自住房的目的是为了实现自身利益最大化。

（3）开发商掌握大量有关自住房的信息（例如自住房的实际房屋质量、实际交通便利程度、实际户型面积等信息），但是政府和消费者可能不完全清楚这些，尤其是住房消费者信息缺失比较严重，处于信息不完全对称状态。

（4）假设自住房的价格函数与需求之间呈线性相关关系：

其中，P(α)为自住房的售价，α为自住房的需求量，λ和β是系数。

（5）假设房地产开发商开发自住房的成本函数是：

其中，θ0，θ1，θ2都是系数，且都大于零。θ0是固定成本，α房屋供给量，θ(α)是自住房开发商的总成本函数。

（6）根据北京市《关于加快中低价位自住型改善型商品住房建设的意见》的文件要求，北京政府部门在开发商竞拍自住房用地及开发过程中应予以支持，比如地价的相对优惠和税收优惠政策等，本模型中对此类优惠统一归入补偿支付，设为εα，其中α是开发商自住房供给量，ε是补偿支付系数。由此可以构建自住房价格的微分状态方程如公式（3）：

其中，P′是自住房的实际价格，λ-βα是消费者在经济能力范围内可以接受的自住房价格，ξ是政府依据市场价格来调整自住房价格的价格调整系数。

2 自住房定价的Stackelberg微分博弈模型构建

在自住房体系中，政府和开发商之间的博弈行为可以抽象为：政府是领导者，首先制定出自住房价格规制的具体政策，开发商作为被领导者，通过调整承诺的自住房供给量来实现自身利润的最大化。具体模型构建过程如下：

（1）参考政府的补偿支付和相关影子成本，当自住房供给和需求达到均衡时，消费者剩余为：

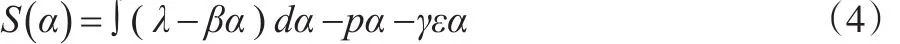
这里，γ大于1，γεα是政府指导开发商开发自住房以及在这一过程中产生的影子成本的总和，∫pαdα是自住房消费者的消费效用；pα是消费者为购买自住房付出的成本。

（2）开发商的利润为净利润和政府补偿支付的总和，设为r(α)：

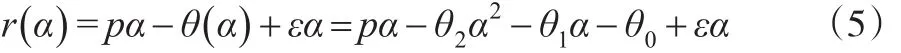
（3）博弈双方的目标函数。政府的目标是实现自住房社会效用的最大化，其独立的决策变量是经济方面的补偿支付。开发商的目标是自身利益最大化，其独立决策变量是自住房的承诺供给量，社会效用假设为自住房消费者剩余与开发商的利润之和。政府和开发商在自住房建设过程中进行动态地、持续地决策，当时间t→∞时，政府和开发商的目标函数是：

政府：

开发商：

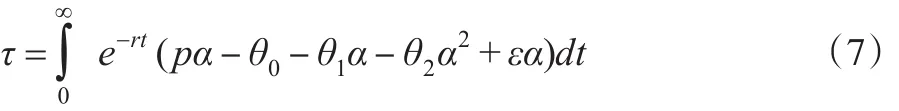
其中，r是社会折现率。

（4）Stackelberg微分博弈模型的构建。根据经典的Stackelberg微分博弈模型的构建方式，可以使用“双层规划”形式来描述政府和开发商之间的博弈过程，即：

其中，θ=f( )p，ε经下层规划可以得到：

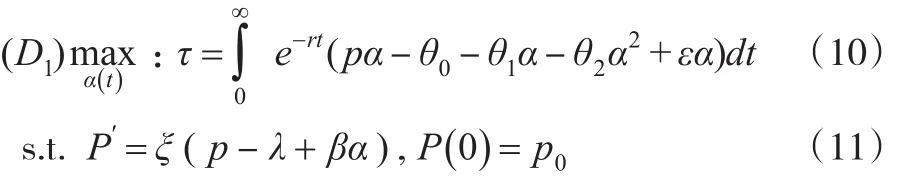
该双层规划模型分别是由U1（上层优化）、D1（下层优化）两个子模型组成。R函数（上层优化）是政府的目标函数，ε(t)是政府的决策变量（经济补偿支付），p0为自住房售价的初值。τ函数（下层优化）是开发商的目标函数，α(t)是开发商的决策变量（自住房供给量）。

3 自住房Stackelberg微分博弈模型的求解

依据Stackelberg主从微分博弈模型的经典求解步骤和规则，本文将采用“逆向归纳”的思想方法和“HJB”方法（Hamilton-Jacobi-Bellman）进行求解（Lions,1983）[8]。

步骤1：依据逆向归纳法，进行第二阶段求解，即首先求出房地产开发商的最优决策（第二阶段最优目标）。

设自住房开发商的二次值函数为v(λ),v(λ)= μ2λ2+μ1λ+ μ0,得 v′(λ)=2μ2α + μ1（其中 μ2、μ1、μ0均为常数），由此构建自住房开发商的HJB方程：

上式的右端是最大化HJB方程式，开发商的最优策略α的表达式可写为：

α 表达式中 μ1和 μ2是v(α)函数的参数，可以用待定系数法来确定。首先在自住房开发商HJB方程的右端代入

式（13）、v(α )、v′(α )，进而根据待定系数法，确定 μ1和 μ2：

根据μ1表达式可知，μ1是ε的一次线性函数，因此为了简化，设 μ1=σ1+σ2ε，其中：然后，把 v′()α 和 μ1=σ1+σ2ε代入到式（13）中，可以得到α的表达式：

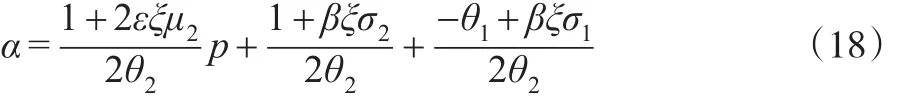
可以看到，开发商的决策变量α是政府决策变量ε以及房价p的一次线性函数。

步骤2：进行第一阶段的求解。在此阶段中，政府作为领导者，首先制定自住房政策。

设政府二次值函数表达式为u(p)，u(p)=η2p2+η1p+η0，可以得到 u′(p)=2η2p+η1（η2、η1、η0都是常数），构造政府的HJB方程：

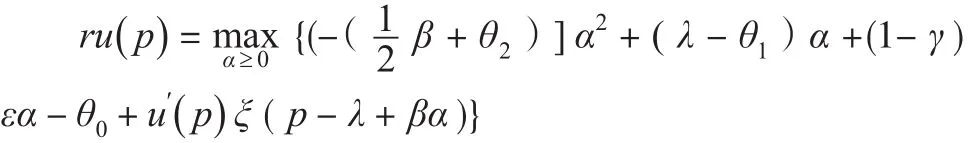
把第二阶段求得的α表达式代入上式，最大化政府HJB方程的右端，可得政府最优策略ε的表达式为：

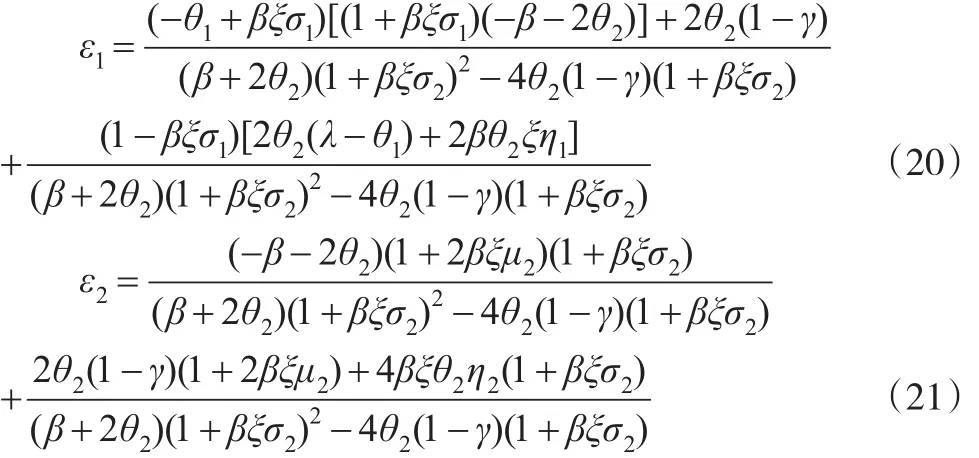
本式中，需要确定η1、η2这两个系数，同样需要由待定系数法求得。可以看出，政府的HJB方程中ε是价格p的一次线性函数，为了化简，设ε=ε1+ε2p，其中ε1、ε2分别为：

将v′()p 和ε=ε1+ε2p带入政府的HJB方程可以得出：

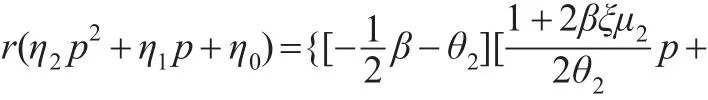
然后，通过待定系数法，依据政府的HJB方程确定v(p )系数η2，η1：

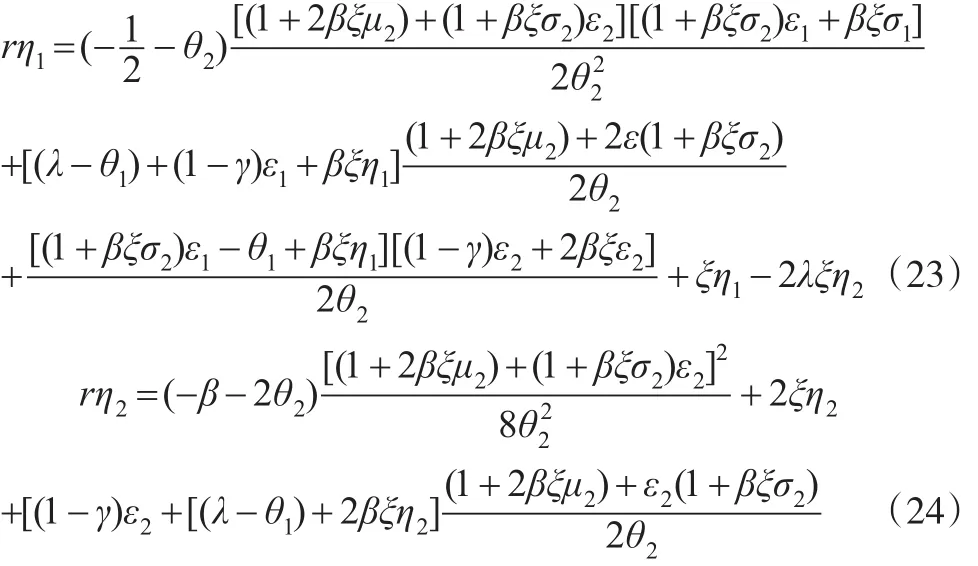
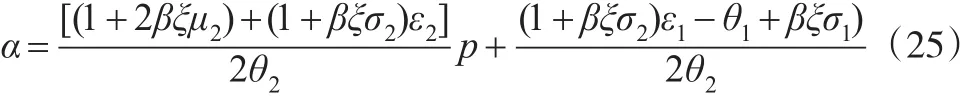
依据逆向归纳法，把第一阶段的最优解ε=ε1+ε2p带入第二个阶段的最优解，可以得到政府的决策变量α：步骤3：微分博弈模型的均衡解。联立自住房销售价格状态方程、政府决策变量、开发商决策变量，可以求得最后的博弈均衡解：

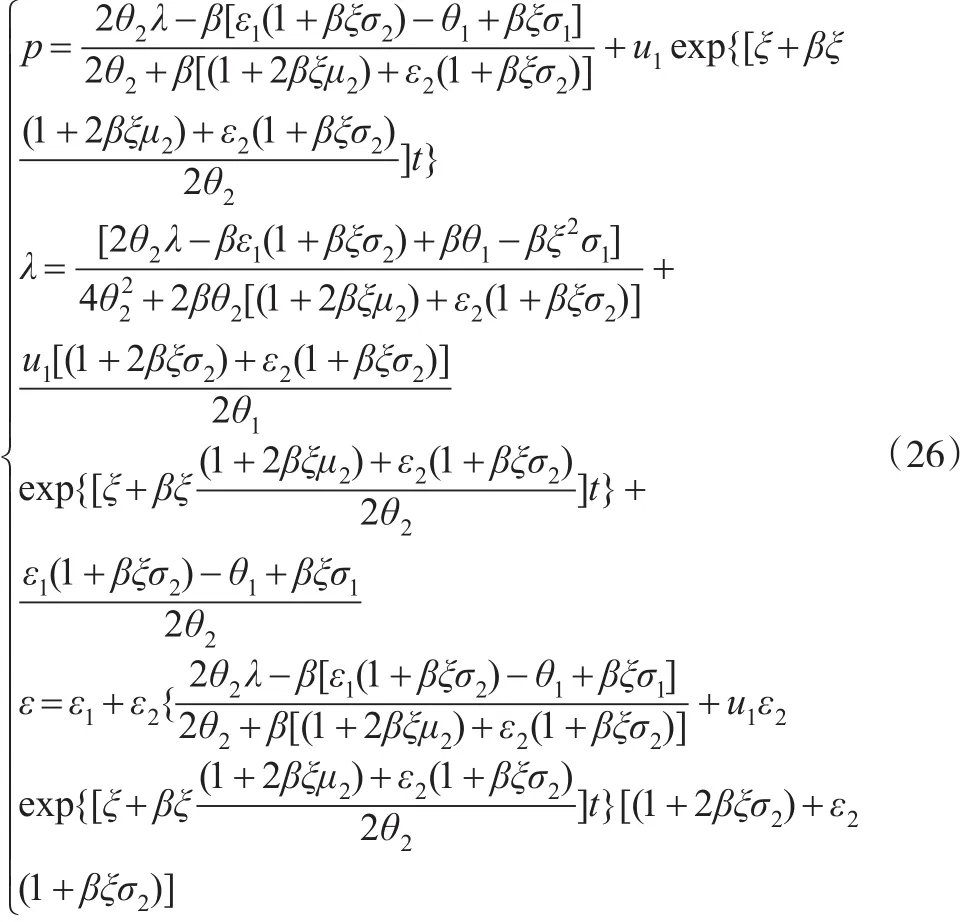
这里，外生变量有：θ1、θ2、λ、r、ξ、γ；内生变量有：σ1、σ2、ε1、ε2、η1、η2；其他的，u1是积分常数，可以由初值p0决定。

4 自住房定价的微分博弈模型赋值模拟

依据北京市自住房的汇总情况，本文认为北京市自住房市场中的参数变量近似满足λ=3500，β=1.5，同时在这一条件下的自住房开发商成本函数满足θ0=3500、θ1=1000、θ2=0.8。社会折现因子取r=0.08，价格调整因子取ξ=0.5，影子成本系数取0.5，那么γ=1.5，并且设定北京市自住房售价平均初值p为18000（元/m2），自住房供给量α单位是“万平方米”。带入模型如下：

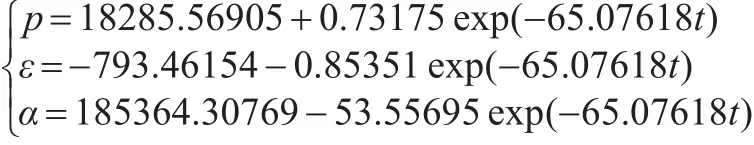
本文依据上述联立方程进行数据仿真分析，为便于各函数图的模拟值进行比较，仿真过程中省去了联立方程中的常数项。

根据图1、图2、图3的函数曲线可以看出，随时间的增加，图1中的自住房的销售价格逐渐下降，图3中的自住房开发商供给量逐渐上升，图2重的政府经济补偿支付也随着时间逐渐提高。模拟结果显示政府的补偿支付逐渐趋于收敛，自住房的销售价格趋于收敛，自住房开发商的供给量趋于收敛，这三个都明显区域收敛于一个特定值。模拟仿真结果也显示，政府不可能无限地对开发商进行补偿支付，开发商也不可能不限地向社会供给自住房，这与社会实际情况也是相吻合的。

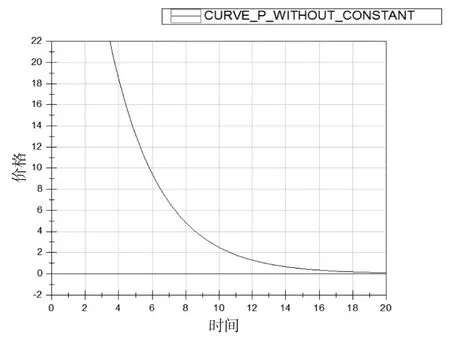
图1自住房平均销售价格p曲线（不含常数项）

图2自住房补偿支付ε曲线（不含常数项）

5 结论

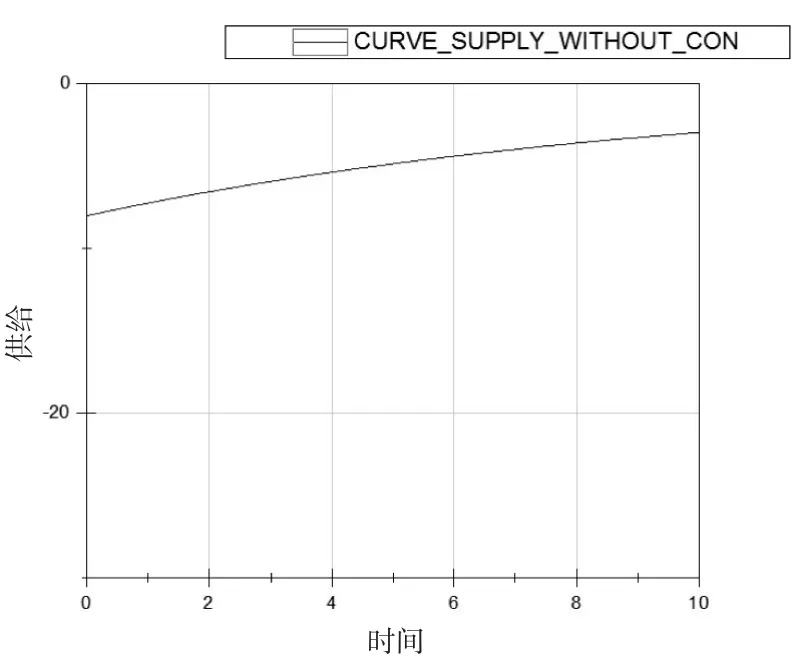
图3自住房供给α曲线（不含常数项）

本文运用Stackelberg微分博弈对北京市自住房价格规制情况进行了研究，研究结果发现北京市自住房的价格将取决于政府与开发商之间长期博弈的结果，北京市政府的政策引导与开发商本身的逐利行为将共同驱使自住房的销售价格逐渐趋于均衡。北京市政府的政策实行和房地产开发商的逐利行为共同推动了自住房自身的定价过程。本文所做的模拟仿真实验与社会实际情况基本吻合，对于测算自住房的合理价格运行区间也有一定作用。

本文的研究结果显示，由于北京市房地产市场的特殊情况，自住房不会冗余，北京市推出这一特殊的房产类公共产品实是为了照顾处于能买房者、家庭困难者之间的“夹心层”人群。因为其具有一定的商品房属性，建造开发与售房过程目前由开发商执行，导致目前在政策执行的过程中，在自住房设计、施工和出售等环节出现一些问题。但总体而言，目前北京市的自住房不能随意废弃，供给量应该维持在一定的水平，以切实保障对自住房边际效用高的人群的住房需求，这样才能有效减少公共住房福利损失。