基于AFSMC的某非平衡身管随动控制研究

陈宇政，高 强，侯远龙，胡继辉，陈机林

（南京理工大学机械工程学院，南京 210094）

0 引言

坦克炮火控系统的性能直接由炮控系统的性能所决定，而炮控系统在设计过程中却存在着诸多难点。在众多不确定因素与各种扰动中，火炮身管运动中的平衡与定位则显得尤为突出，因此，对于火炮身管的精确定位控制与身管运动中产生的非平衡力的平衡则成为首要必须解决的问题。由于火炮身管平衡过程中存在着诸多非线性因素，若采用传统的控制策略则难以取得理想的控制效果。滑模控制是一类极具特色的非线性控制，可以驱使系统根据状态的变化有目的地沿着预设的目标轨迹作小幅度、高频率的上下运动，即所谓的“滑动模态”运动。这种“滑动模态”是允许根据实际需要进行调整的，并且不受外界干扰和系统参数改变的影响。因此，处在滑模运动状态下的系统会具备很强的鲁棒性［7］。然而在滑模切换过程中出现的抖振现象却是传统滑模控制中的一大弊端。因此，消除系统抖振成为学者们研讨滑模控制的关键所在。

文献［8］在传统滑模控制的基础上加入自适应模糊控制，并把该控制策略应用在导弹电液伺服机构的跟踪控制上，通过仿真可知，该方案对于参数摄动及负载扰动，具备较强的动态响应能力，较小的稳态精度和较强的鲁棒性。文献［9-10］把自适应模糊滑模控制理论运用于火箭炮位置随动控制的机电耦合特性中，仿真结果表明，该方法不仅保持了滑模控制中的抗扰动性能，而且有效地降低了系统存在的抖振。从上可知，在滑模变结构控制中引入自适应模糊方法，对消除抖振有很大的作用。因此，本文采用了一种自适应模糊滑模变结构控制（AFSMC）的智能控制策略，并把它应用在坦克炮身管定位与平衡中。仿真试验证明，该控制器能有效克服外界干扰，保证了系统的静、动态特性，有效降低了滑模变结构控制中固有的抖振现象，同时具有很强的鲁棒性。

1 系统组成及数学模型的建立

1.1 系统组成及工作原理

炮控系统实质上是一种电液位置伺服控制系统，负责控制火炮高低向调炮工作过程。主要包括两腔液压缸，电液伺服阀，伺服放大器和负载身管。如图1所示：

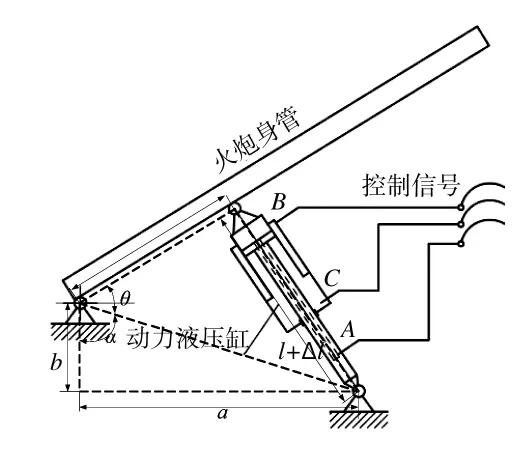
图1 火炮身管升降机构简图

在执行高低向调炮任务时，对其电液位置伺服控制系统进行简化，如图2所示：

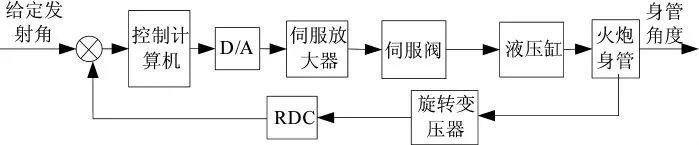
图2 某坦克炮控高低向调炮控制系统框图

某坦克炮进行高低向调炮工作时，主要由以下几个流程组成：

1）根据作战需要，给定预先设定好的坦克炮身管的发射角度；

2）发射角度经过计算机的解算后，由计算机输出相应的控制信号；

3）控制信号经过D/A模块转换后输出炮控系统模拟信号，伺服放大器将得到该模拟信号；

4）伺服放大器对该模拟控制信号进行一系列的处理后，输出相应的控制电流，并直接输入到电液伺服阀中，由此控制着电液伺服阀的换向和开度大小；

5）电液伺服阀控制着流入液压缸中的液压油，以此控制液压缸中活塞杆的来回伸缩，最终使坦克炮身管到达预期的发射位置；

6）旋转变压器对坦克炮身管的实际位置进行测量，然后将测量到的模拟信号传递给RDC转换模块进行转换得到数字信号，该数字信号将输入到计算机中，从而形成一个完全的闭环系统。

1.2 系统模型的建立

在系统建模之前，先作如下假设：

1）忽略管道内压力损失和管道动态；

2）两腔作用活塞缸筒的面积相等；

3）阀具有很好的响应特性；

4）忽略阀中流体的压缩特性；

5）在管道和缸体腔内不会出现压力饱和现象；

6）忽略液压油的泄漏及缸筒与油液的弹性。

首先建立该电液伺服系统的流量方程，并通过余弦定理把身管转角θ融入到方程中，最后经过拉氏变换，可得：

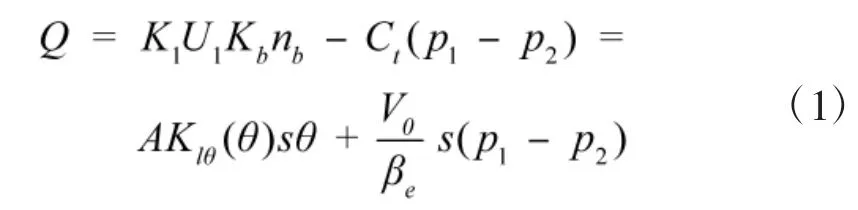
式中：K1为电压放大系统；U1为输入控制电压；Kb为泵的排量梯度；nb为泵的转速；Ct为总泄露系数；p1为负载压力；p2为补油压力；A为液压缸活塞面积；Klθ（θ）为液压缸活塞伸缩速度和身管角速度转换系数；θ为身管旋转角度；V0为压力为p1的液体容积；βe为有效体积弹性模数。

通过对该电液伺服系统的力矩平衡方程也进行拉氏变换，可得：

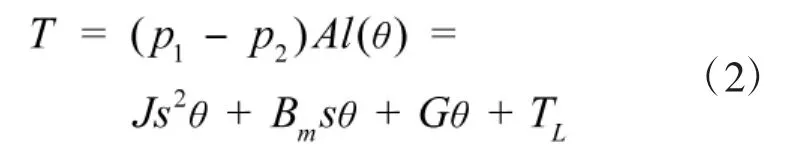
式中：l（θ）≈Klθ（θ）；TL（s）=TG（s）-Tp（s）；J为转动惯量；l（θ）为液压缸活塞缸筒输出力对A点的力臂；Bm为粘性阻尼系数；G为负载弹性刚度；TL为不平衡力矩。

取系统状态变量为x=［x1x2x3］T，其中，，把力矩平衡方程和流量连续性方程联合，消去（p1-p2），则系统的状态空间方程为：

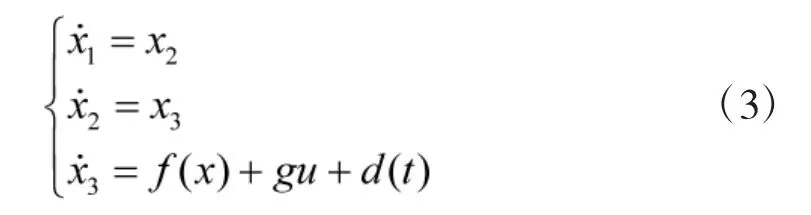
由于带弹量的改变会导致系统的转动惯量J大范围地变动，并且随着工作条件的变化也会引起不平衡力矩TL、总泄露系数Ct、粘性阻尼系数Bm的变动。因此，f（x），g，d（t）的各参数均是时变的，均是不确定参数。

2 传统滑膜控制器（SMC）设计

假设位置指令θd，则误差为e=θd-θ。根据线性化反馈方法，控制器设计为

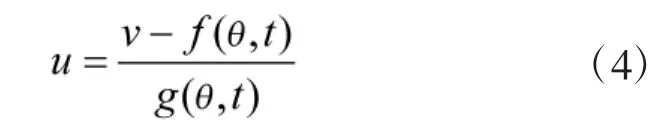
其中，v为控制器的辅助项。

将式（4）代入式（3）得

设计v为

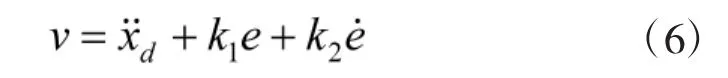
其中，k1和k2为正的常数。

将式（6）代入式（5），得

由于此方法设计的模型需要精确的模型信息，无法克服外界扰动，故在传统滑模控制基础上引入自适应模糊控制律。

3 自适应模糊滑模变控制器设计

3.1 基本的模糊系统

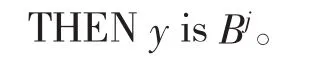
采用乘积推理机、单值模糊器和中心平均模糊器设计模糊系统，则模糊系统的输出为：

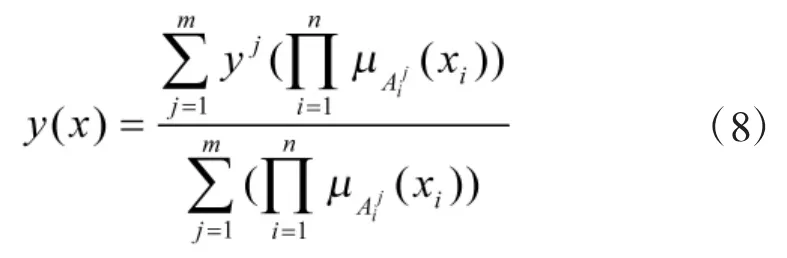
引入向量 ξ（x），式（8）变为：

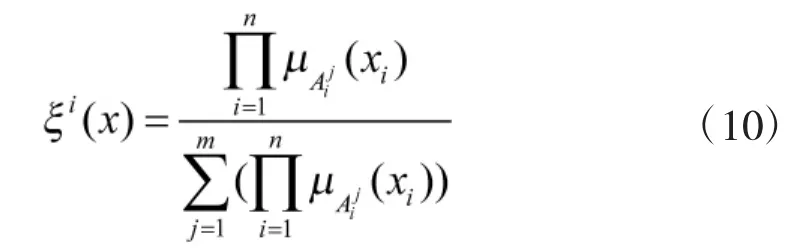
3.2 自适应模糊滑模变控制器的设计

定义切换函数为：

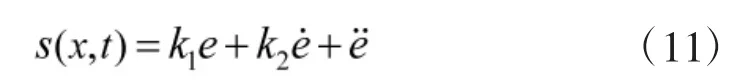
将滑模控制律设计为：

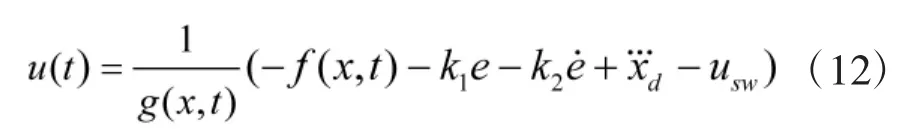
则

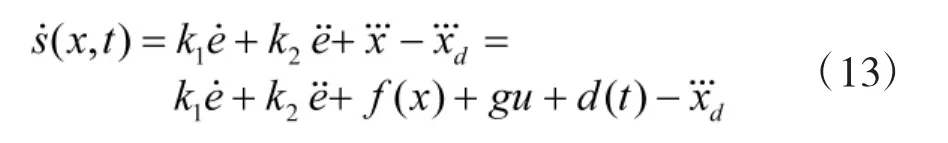
将式（3）和式（12）代入式（13），得：

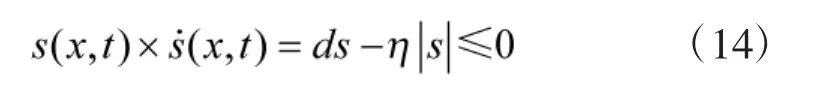
由于f（x），g，d（t）各参数均是时变的，故其无法确定，控制律式（12）不适用。因此，本文采用模糊系统逼近。

采用乘积推理机、单值模糊器和中心平均模糊器设计模糊系统，模糊系统的输出分别为则控制律变为：

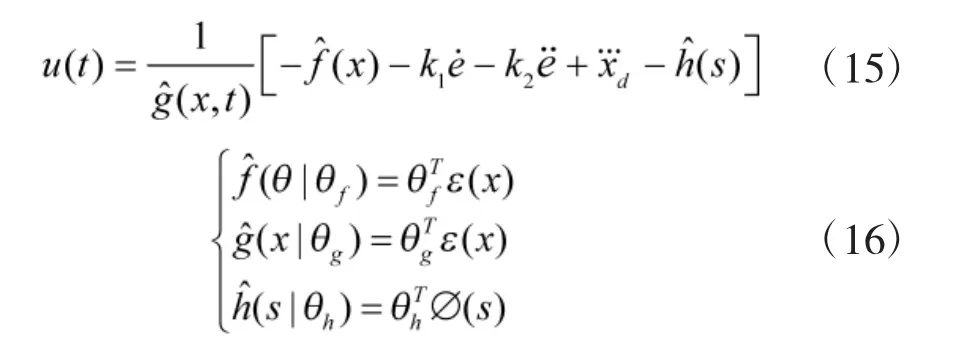
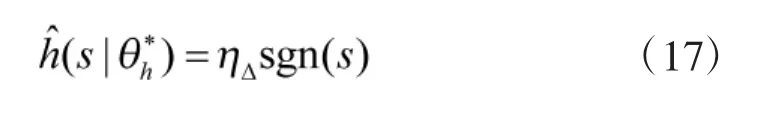
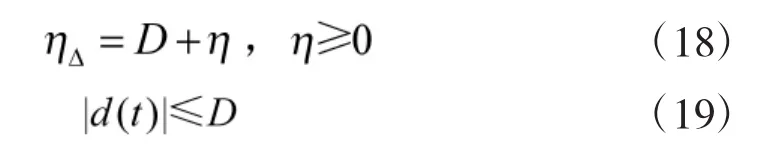
设计自适应律为：

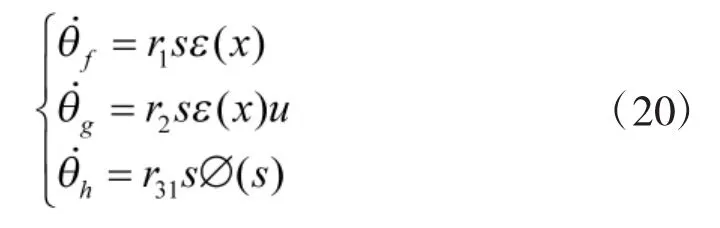
自适应模糊滑模控制系统的结构如图3所示：

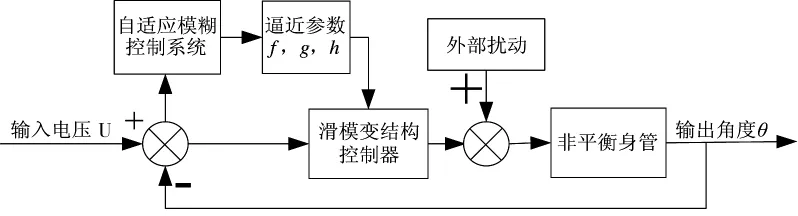
图3 自适应模糊滑模控制系统

4 实验仿真

通过以下5种隶属函数对系统进行模糊化：

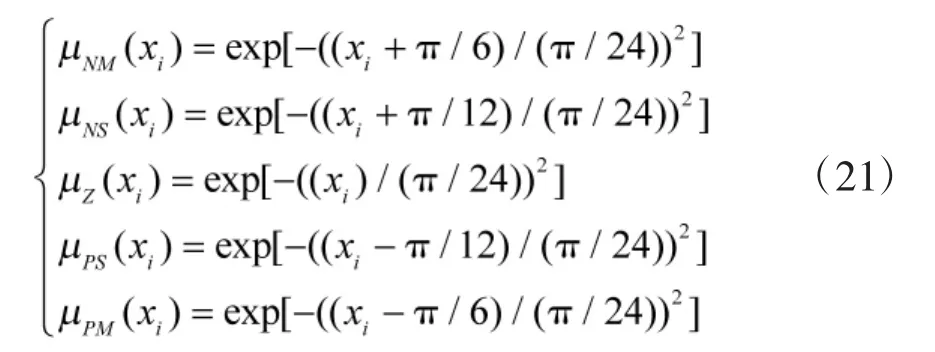
则用于逼近f（x）和g的模糊规则分别有25条。

根据以上5种隶属函数运用matlab编译程序，可得到隶属函数图，如图4所示：

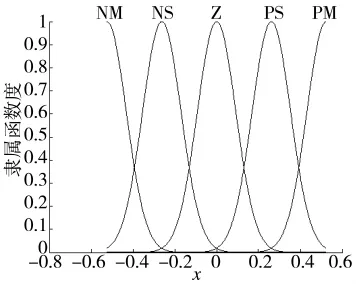
图4 f（x）和g的隶属度函数图

定义切换函数s（t）的隶属函数为

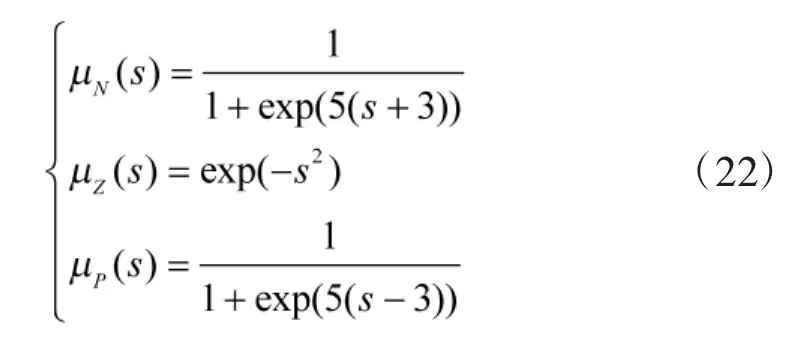
通过对该电液伺服系统的动态仿真试验来检验本文所设计的控制策略的有效性，具体系统参数为

首先对系统的阶跃响应进行仿真，仿真过程采用与传统滑模变结构控制（SMC）进行对比，设定角度目标值为10°，进行仿真，仿真时间为10 s。对于外部的扰动采用一个角度在±0.3°范围内波动的随机信号进行模拟。通过对图5、图6的阶跃响应图中两条曲线分别进行比较可知，本文设计的控制器（AFSMC）到达稳态用时1.4 s，无超调。而传统滑模控制（SMC）到达稳态用时2.2 s，在抗扰动能力上，本文所采用的控制策略（AFSMC）基本无抖动，具有较强的抗干扰能力，而传统滑模变结构控制（SMC）出现了较大的抖动，并且出现了超调现象，稳态误差最大时可达0.15°，由此可见，采用自适应模糊滑模变结构控制（AFSMC）在抗干扰性能，消除抖振上远优于传统滑模变结构控制（SMC），也极大地提高了系统到达稳态的时间。

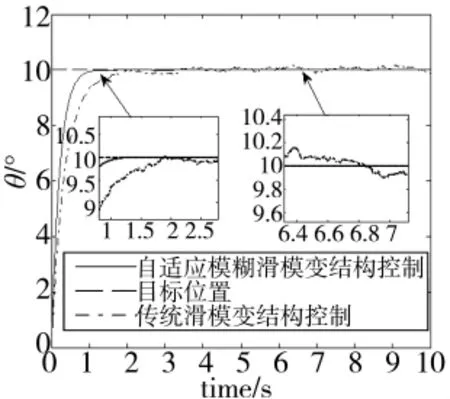
图5 不同控制器在有随机扰动下的阶跃响应曲线

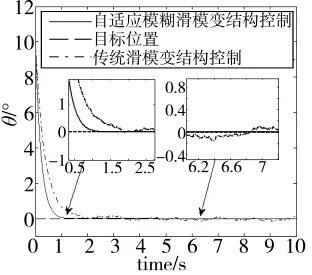
图6 不同控制器在有随机扰动下的误差曲线

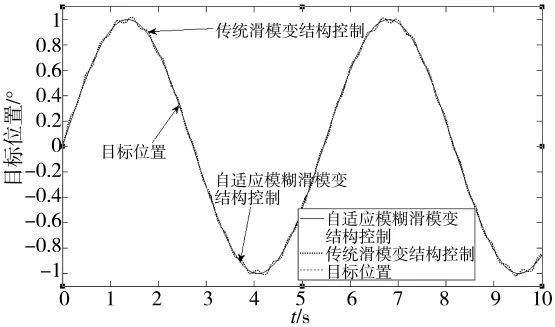
图7 不同控制器的正弦跟踪曲线

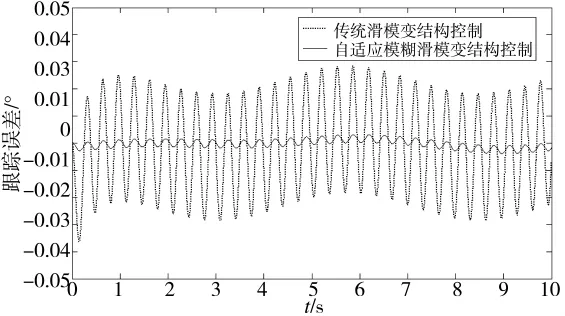
图8 不同控制器的正弦跟踪误差曲线

为了进一步验证本文所设计的控制策略对系统抗干扰，消除传统滑模变的抖振问题，又对系统进行了正弦跟踪仿真试验。系统在作正弦跟踪时，加入以16.7 rad/s的角频率、幅值为3°的正弦干扰，其仿真结果曲线如图7、图8所示。通过对比可知，采用传统滑模变结构（SMC）控制时，系统产生抖动，最大跟踪误差为0.037°；而采用自适应模糊滑模控制（AFSMC）时，系统抖动基本消除，最大跟踪误差为0.003°，由此可见，在传统滑模变基础上加上自适应模糊控制能更好地跟踪目标曲线，也能较好地消除滑模变结构存在的抖振，使炮控系统具有较好的鲁棒性［11-12］。

5 结论

本文对于一种非平衡火炮身管的平衡定位问题，设计了一种基于自适应模糊滑模变结构控制（AFSMC）的控制方案。通过仿真结果可知，该方法较好地消除了外界扰动，有效地抑制了传统滑模变结构（SMC）特有的抖振问题，较好地保持了滑模控制特有的抗摄动性能，并且对结构参数不确定性具有很强的鲁棒性，适用于高精度的电液伺服系统的鲁棒控制。