装备模拟电路UKF-WRNN软故障诊断

郭 峰，王春兰，李胜厚，杨国洲

（1.西京学院，西安 710123；2.空军工程大学空管领航学院，西安 710051）

0 引言

随着电子装备性能的日益提高，其复杂程度也越来越高，电子设备的电路板功能越来越强大，但结构却越来越复杂，种类也越来越繁多，尤其是模拟电路的容差等问题引起的软故障，极易引起电路和整个装备系统性能的逐渐恶化，必须对其准确诊断和定位，也是当前的研究热点。

模拟电路的软故障诊断本质上是一个模式识别和分类问题，即将给定的故障数据划分为正常数据和故障数据。随着模拟电路故障诊断技术研究的深入，出现了故障字典法、参数辨识法、故障验证法等诸多软故障诊断方法［1-3］，实践和数值分析表明，元器件发生软故障时，其参数可能在零到无穷大之间连续变化，而不同的偏移会引起不同的电路响应，电路的状态数可能是无穷的。将这些诊断方法用于软故障诊断，其计算量是现有计算机水平无法胜任的［5］。神经网络技术的出现，完全改变了模拟电路软故障诊断的既有模式，它采用新颖的黑箱建模思想，具有较强的学习、识别、记忆和联想功能，也引起了领域内的极大关注［6-8］。然而，神经网络遵循经验风险最小化原则，其准确率不高、收敛较慢等缺陷没有得到有效解决，限制了推广。研究表明，小波神经网络性能较之前者有了很大改善，理论也更趋于严密，是公认的神经网络替代方法［9-10］。

基于此，本文在多分辨率变换提取故障样本基础上，提出一种采用自适应UKF算法训练小波RBF神经网络（Wavelet RBF Neural Network，WRNN）的模拟电路软故障诊断方法，并通过仿真验证其有效性。

1 小波RBF神经网络

小波神经网络是利用小波变换构造的一种新型神经网络，它系统地融合了小波变换的时频局域特性和神经网络的自学习功能，也被视为神经网络技术的深化推广。本文在RBF神经网络基础上构建了一种多输入多输出（MIMO）的小波神经网络（WRNN），如图1所示，与RBF神经网络不同之处是将网络的隐节点激励函数替换为小波基函数［11］。

图1 小波RBF神经网络

网络输出函数可采用小波基函数拟合如下

将网络参数 whj，ah，bh视为向量 θ，WRNN 的状态空间模型可表示为：

式中，uk代表网络输入，yk代表网络输出，g（θk，uk）为参数化的非线性函数。ηk为过程噪声，是均值为零，方差为Qk的高斯白噪声；μk为测量噪声，是均值为零，方差为Rk的高斯白噪声。

实际上，对WRNN训练是指对其状态空间模型的 θ（whj，ah，bh）进行最优估计的过程，采用不同算法优化参数向量θ就形成不同WRNN算法。

2 自适应UKF算法

2.1 UKF算法

UKF算法是Julier提出的一种基于近似分布的Kalman滤波算法，UT（Unscented Transformation）是该算法的核心，它采用确定性采样策略逼近非线性分布，能以更高精度估计非线性系统的后验均值和协方差［12］。设状态方程与观测方程为

式中，过程噪声ωk和观测噪声υk分别为协方差矩阵Qk和Rk的高斯白噪声。UKF算法步骤如下：

2.1.1 初始化

2.1.2 Sigma点采样与权重确定

2.1.3 时间更新

2.1.4 预测量测采样点

2.1.5 量测更新

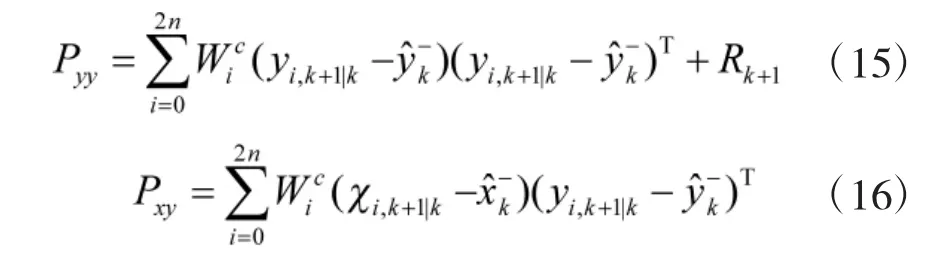
2.1.6 状态更新

式中，Kk+1为Kalman增益矩阵。

2.2 AUKF算法

与EKF算法相比，UKF算法的估计精度更高，并具有更强的鲁棒性及稳定性。然而，在使用中，UKF算法对初始值比较敏感。如初始值选取不当，会对式（10）和式（11）的计算结果造成影响，进而影响到式（14）的计算值；此外，状态模型的异常扰动也可能对k-和k-的构造造成影响。基于此，对UKF滤波过程可采用方差膨胀原则［13-14］，对k-和k-的协方差矩阵进行自适应调整（即AUKF算法），以改善滤波估计效果。那么，引入的自适应因子（0＜≤1）可由下式给出

根据以上调整过程，当初始值存在偏差或状态模型出现异常扰动时，则＜1，也就是使状态模型误差的贡献尽量小，而当偏差与异常扰动较大时→0，此时状态模型误差的贡献最小，算法将趋于发散。

3 基于AUKF的WRNN训练算法

采用AUKF算法训练WRNN的步骤如图2所示，初始化参数值及其方差，进行时间更新，通过UT变换产生Sigma点后进入WRNN并向前传播，并引入自适应因子计算方差、协方差和Kalman增益矩阵，最后进行参数值和误差方差的量测更新，循环往复，直至满足收敛条件为止［10］。

图2 基于AUKF的WRNN训练流程图

4 基于多分辨率分解的故障特征样本集构建

模拟电路的输出信号中含有丰富频率成分，发生故障时，这些频率成分有些被削弱，有些被加强，造成同一成分相对于电路正常时会有所不同。因此，可考虑通过多分辨率变换将输出信号中的一些频率成分变化提取出来，表征各个故障，用于故障诊断实验［15-16］。

多分辨率变换概念最早由Mallat与Meyer提出，并随之给出离散正交二进制小波变换算法，即任何函数f（t）∈L2（R）都可分解为

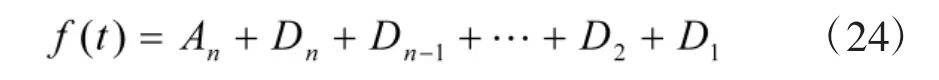
式中，f（t）表示待分解信号，A表示低频近似部分，D表示高频细节部分，n为分解层数。由图3所示的三层树型结构可知，多分辨率变换仅对低频空间作深入分解，而不考虑高频部分，以构造一个频率上高度逼近L2（R）的正交小波基。

图3 三层多分辨分析树型结构

多分辨率变换按照分辨率2-j将空间L2（R）先分解为嵌套的闭子空间序列{Vj}j∈Z，并按塔式分解将L2（R）分解为正交小波子空间序列{Wj}j∈Z。根据多分辨变换原理，Wj的闭包能够覆盖整个空间，并满足，若假设，则可将V0分解为，其中，Wj为Vj-1中Vj的正交补，则f（t）可以分解为：

式中，fN（t）项为f（t）在尺度N下的逼近，它描述f（t）分辨率不超过2-N的成分；而gj（t）项描述f（t）分辨率处于2-j到2-j+1之间的细节成分。为尺度函数，其为VN的标准正交基；为小波函数，其为Wj和L2（R）的标准正交基。

模拟电路故障时，输出信号变化并不明显，需要依据小波基类型和信号长度选择合适分解尺度，对输出信号进行多分辨率分解，即通过各层分解系数反映信号中不同成分的突变特征。

5 实验仿真

实验环境：Pentium IV 2.4 GHz CPU，4GB DDR内存，80 GB+7 200转硬盘；Windows 7操作系统。实验中，模拟电路的故障样本采集采用ORCAD 10.5软件中的Capture CIS模块来完成；所涉及算法均采用MATLAB软件编程并调试运行。

5.1 Sallen-Key滤波器电路及其故障集

实验以Sallen-Key带通滤波器作为模拟电路故障诊断对象，电路中各元器件标称值如图4所示。设电阻的正常容差范围为5%，电容的正常容差范围为10%，且输出端Out为唯一可测试节点。为简化问题，本章仅研究电阻和电容的单个软故障，而不考虑多故障和硬故障。

图4 Sallen-Key带通滤波器

利用软件PSPICE对该电路进行仿真，通过交流小信号灵敏度分析，综合比较各元件对输出波形影响的灵敏度后，可知电路的输出响应波形受R2、R3、C1和C2的变化影响最大。因此，可确定故障集中包含 8 种故障模式，即 R2-、R2+、R3-、R3+、C1-、C1+、C2-和C2+，其中，符号+和－分别表示偏大软故障和偏小软故障，偏差标称值都为±50%，再加上正常模式总共9种模式。采用“0-l”法可得AUKF-WRNN输出层的8个输出节点的期望输出向量，如表1所示。

表1 AUKF-WRNN故障诊断系统的期望输出特征

AUKF-WRNN诊断思路：首先，设定电路元件的故障模型，再进行蒙特卡洛分析，根据分析结果确定故障集；然后，对故障集中的各个模式下的样本信号提取故障特征，对故障特征进行核主元分析后，构造训练样本集，用于AUKF-WRNN训练；最后，将待诊断信号进行相应处理后得到的测试集输入训练好的AUKF-WRNN，根据输出结果，就可以诊断出模拟电路的故障状态。

5.2 模拟电路样本集构造

在图4中，将电路输入电源Vin设定为正弦波输入激励，电压幅值为4 V，电压频率为1 kHz。扫描的起始时间为0.25 ms，终止时间为1.5 ms，扫描的步长为0.5 μs，根据各个模式的特征对故障元件进行故障模型设置，无故障元件在各自的正常容差范围内，将电路的特性分析设定为瞬态分析，利用软件PSPICE进行蒙特卡洛分析，可得到各故障模式下的输出波形，仿真后每个模式输出50个瞬态响应信号波形，对波形采样后得到的数据保存到PSPICE软件的输出文本文件中。

读取*.Out文件中各个波形的在0.25ms～1.5ms变换构建样本条件下的4种算法建模性能对比。而下页表3比较了隐节点数为15时4种模型对各个模式的正确诊断结果，其中，C表示正确诊断数；R表示正确诊断率。下页图5对4种模型的训练收敛曲线进行了对比，其中，MSE表示网络训练的均方根误差。图6分析了所选取隐节点数H对故障诊断模型测试性能的影响。

从实验结果可看出，UKF-WRNN和AUKFWRNN在训练错分数、测试错分数和收敛性都优于WRNN，说明经UKF和AUKF训练后的WRNN性时段内的采样数据，得到500个信号。选择db2小波作为小波基函数对采集的数据进行5层多分辨率分解，得到 6个分解系数序列（D1，D2，D3，D4，D5，D6，A），求取各高频系数序列和低频系数序列的能量，并对其进行归一化后，构成6维向量作为每个信号对应的输入向量，再与对应的期望输出向量组合，就可以得到500组样本集，随机选取200组用于训练AUKF-WRNN模型，剩下的300组用于测试。

5.3 实验分析

为验证算法有效性，实验分别采用WNN（BP算法）、WRNN（梯度下降算法）、UKF-WRNN和AUKFWRNN算法对被测电路进行了故障诊断测试和性能对比。参数 whj，ah，bh初始值都取［-0.5，0.5］内随机数，最大训练次数为500。实验中，设网络输出层任意一个节点的实际输出值与期望输出值差值的绝对值大于判定值0.3，则认为诊断错误。对于UKF和AUKF，Rk的对角线元素可取为0.001；Qk的对角线元素可取为0.1。

表2 诊断模型训练和测试性能对比

表2给出分别采用波形特征提取和多分辨率能确实优于传统的梯度下降训练算法的WRNN。而相对于UKF-WRNN，AUKF-WRNN表现出了更好的训练、测试和收敛效果，其仅仅通过不到200次训练，模型就能够收敛，且R2-、R3+、C2+和正常模式的诊断正确率甚至达到100%，总正确率达到96.7%，并且隐节点数从12～17内取值时，测试样本错分数都控制在10以下，这表明，使用AUKF训练WRNN模型，更易于实现，性能得到了改善，有效刻画了系统的非线性特征，进而确立了AUKF-WRNN在模拟电路软故障诊断中的优势。另一方面，通过表2对比可知，较之波形特征参数信息，利用多分辨率变换法提取的样本，可以取得更好的模拟电路故障诊断效果，这一特性对于AUKF-WRNN的推广非常重要。

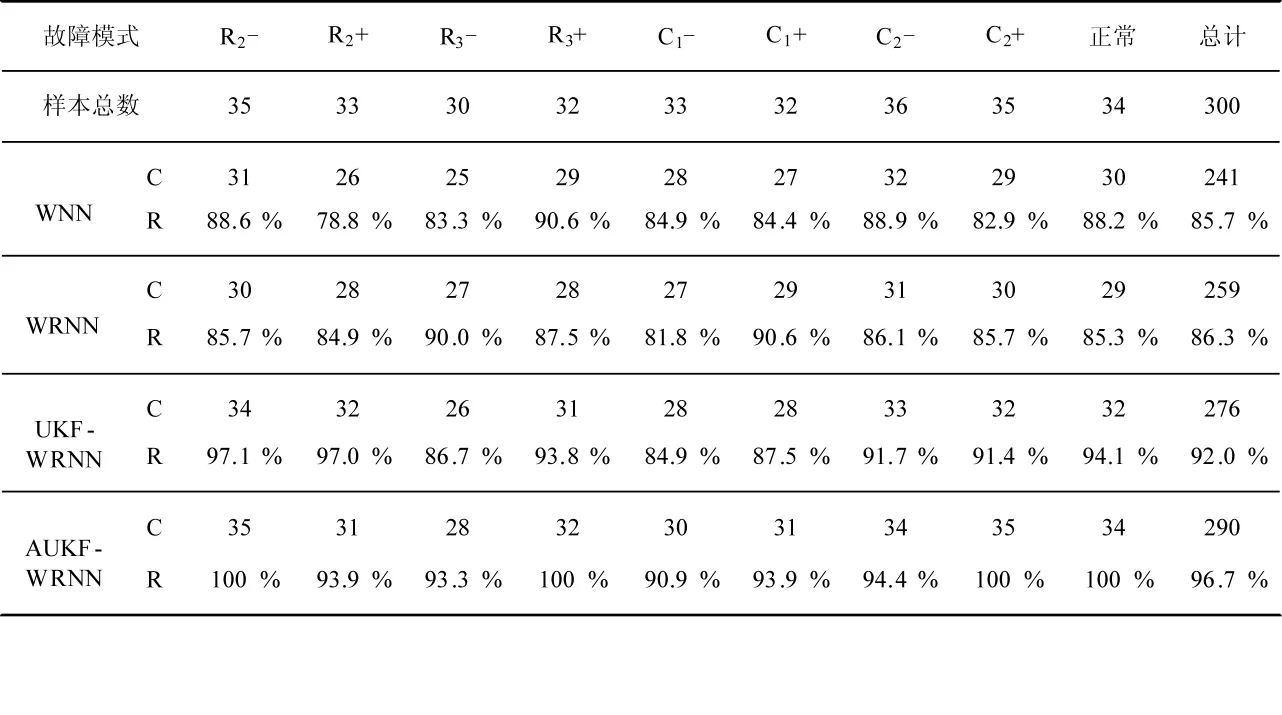
表3 诊断模型正确诊断结果对比

图5 训练收敛曲线对比

图6 隐节点数对模型测试性能的影响

6 结论

为提高军用装备模拟电路软故障的诊断正确率问题，在多分辨率变换获取软故障样本基础上，提出了一种采用UKF算法训练小波RBF神经网络的软故障诊断方法。Sallen-Key带通滤波器的仿真结果表明，基于该UKF算法训练的WNN模型，收敛快，诊断精度高，较之梯度下降算法和UKF算法，诊断效果得到了较大提高，此外，相比于波形特征参数信息，利用多分辨率变换法提取的样本，可以取得更好的模拟电路故障诊断效果，从而为模拟电路的软故障诊断问题提供了一种新的手段。