外掺MgO对水工隧洞混凝土温度徐变应力的影响

2018-08-21陈妤杜志达王成山

水利与建筑工程学报 2018年4期

陈妤，杜志达，王成山

(1.大连理工大学建设工程学部，辽宁大连116024；2.辽宁省水利水电勘测设计研究院，辽宁沈阳110000)

随着我国水利工程项目建设的不断发展，水工隧洞混凝土衬砌的裂缝问题开始逐渐受到人们的重视[1-7]。研究表明，混凝土的温度应力是隧洞衬砌产生裂缝的重要原因[4-6]。我国早年所建工程的水工隧洞一般只是通过简单的养护来进行防裂[8-10]，随着对衬砌混凝土温控防裂的不断重视，近年来开始逐渐采取通水冷却、提高粉煤灰掺量、控制衬砌分段长度以及冬季挂帘保温等防裂措施[11-15]。研究表明，在混凝土中掺加MgO膨胀剂可以有效减少混凝土温度裂缝的产生[16-17]，多项工程的成功运用进一步证实了这一点[18-19]。到目前为止，外掺MgO混凝土已经在许多水利工程的基础约束部位乃至全坝段的浇筑上得到了成功应用[20-22]，但是将其应用于地下工程混凝土衬砌的研究成果却比较少见。本文基于ANSYS的UPFs二次开发，结合辽宁省某工程输水隧洞进行了长历时的衬砌混凝土温度徐变应力计算，在考虑混凝土掺加MgO外加剂后自生体积变形的情况下对外掺MgO在混凝土衬砌温度应力上的补偿效用和规律进行了探讨。

1 考虑混凝土温度徐变效应的有限元计算

由于混凝土材料本身属于弹性徐变体，所以在恒荷载的作用下其变形会随着时间的推移而不断增长，这种现象称为徐变。对于混凝土温度应力的有限元计算，通常会采用初应变法来计算徐变的影响[23]。现将具体原理介绍如下：

把时间细分为一系列时段Δτ1、Δτ2…Δτn，其中Δτn=τn-τn-1。

设徐变度为

(1)

则有徐变应变增量：

(2)

其中

(3)

{ωsn}={ωs,n-1}e-rsΔτn-1+

(4)

{ωs1}=Δσ0ψs(τ0)

(5)

应力增量可表示为

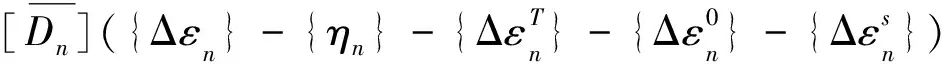
(6)

其中

(7)

(8)

单元的节点力增量为：

(9)

其中

单元刚度阵

(10)

徐变、温度、自生形变、干缩对应的单元节点载荷增量分别如下：

(11)

(12)

(13)

(14)

在有限元里由平衡方程

(15)

分别代入节点力和相应的荷载，则对整体而言上式可转化为

(16)

根据式(16)求得每个节点各自的位移增量{Δδn}后，再由应力-应变关系，即得到每个节点对应的{Δσn}。进行累积相加后即得最终所求应力值：

{σn}=∑{Δσn}

(17)

本文将掺加MgO之后混凝土微膨胀变形引起的应变增量作为自生体积变形增量的一部分考虑进式(16)进行计算，并将其产生的荷载增量和外力等产生的荷载增量进行相加，从而最终由式(17)得到各单元的应力值。

为了在ANSYS中实现上述计算，本文对ANSYS的UPFs进行了二次开发。在利用瞬态热分析求得隧洞施工期及运行期温度场的基础上，由ANSYS中UPFs的二次开发对每一个荷载子步结束后的状态变量和应变增量进行更新，从而最终计算得到考虑徐变效应的隧洞衬砌单元的温度应力值。具体的程序及计算方法可参见文献[24-25]。

2 工程实例仿真分析

本文以辽宁省某工程输水隧洞为例进行了长历时的应力仿真计算。由于该输水隧洞埋藏较深，隧洞混凝土衬砌的环境温度主要考虑为地温、气温以及隧洞在运行期间的水温变化。本文取隧洞深部的环境初始温度为14℃，地温和环境初始温度相同。

2.1 计算条件

2.1.1 围岩和C35混凝土的热力学性能

根据该工程中混凝土抗裂试验研究的阶段性成果，分别选取围岩和衬砌混凝土的相关计算参数如表1所示。

表1 围岩与衬砌混凝土热、力学计算参数

参照文献[26]，混凝土龄期t时的绝热温升表达式为：

(18)

式中：Q0为最终水化热，取510 kJ/kg；W为包括水泥及粉煤灰的胶凝材料用量，取408 kg/m3；p为粉煤灰掺量的百分数，20%；t为龄期，d；m、n为常数，取0.69、0.56。

2.1.2 衬砌混凝土的徐变

在温度应力分析中采用徐变度的计算表达式如下：

C(t,τ)=(0.23/E0)(1+9.2τ-0.45)[1-e-0.3(t-τ)]+

(0.52/E0)(1+1.7τ-0.45)[1-e-0.005(t-τ)]

(19)

式中：E0为弹性模量的最终值，GPa。

2.1.3 衬砌混凝土的自生体积变形

为了分析掺加MgO对衬砌混凝土温度徐变应力的影响，本文采用对比研究考虑混凝土自生体积变形计算的两种情况：(1) 混凝土中不掺加MgO的自生体积变形；(2) 掺加3%MgO的自生体积变形。

由于本输水隧洞衬砌混凝土未做自生体积变形试验，因此采用了附近水利工程中相近混凝土配比的自生体积变形试验成果，如图1所示。

图1混凝土自生体积变形试验曲线

由图1可以看出，在刚开始浇筑的24 h内素混凝土处于体积膨胀的状态，但在24 h过后很快就转变为长时间的体积收缩变形。在大约经历了100 d之后，素混凝土的体积变形维持在了-20.41×10-6左右。而掺加了3%MgO(MgO掺量是胶凝材料总量的3%)的混凝土则始终处于体积变形随龄期单调递增的状态。由于最终的膨胀量是一定的，在经历了大约100 d之后，掺MgO混凝土的体积变形维持在了76.82×10-6左右。

2.2 计算模型及边界条件

2.2.1 有限元计算模型

在仿真计算过程中，选取Ⅲ类围岩的有压段衬砌结构作为分析计算的对象。该衬砌结构断面呈城门洞型(见图2)，其中一次支护采用喷射C30混凝土，厚度0.1 m，二次衬砌采用厚度0.3 m的C35混凝土，围岩在径向上选取10 m的范围进行有限元计算。衬砌结构和围岩在温度场计算过程中均采用Solid 70实体热单元，应力场计算时采用Solid 185固体结构单元。结构断面模型在进行有限元网格划分时共划分单元4 524个，一次支护混凝土和二次衬砌的计算网格厚度均为0.05 m。隧洞围岩采用渐变网格剖分分为20份。输水隧洞的有限元计算模型见图3。

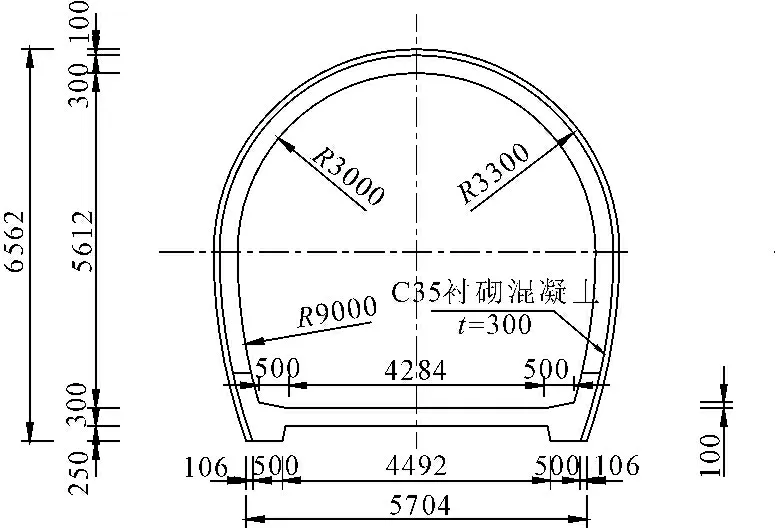
图2 隧洞断面结构示意图(单位：mm)

图3有限元计算模型示意图

2.2.2 计算边界条件

在选取温度场计算的边界条件时，由于隧洞二次衬砌的内表面在施工阶段和空气存在热量的对流交换，所以设为对流换热边界条件，属于第三类热学边界条件。在输水隧洞运行期间，由于有压隧洞衬砌的内表面和水流存在直接接触，所以给予已知的水温第一类温度边界条件。同时由于考虑到围岩的外围距离隧洞衬砌比较远，几乎接近于地温，所以对于衬砌周边给予已知的地温边界条件，即第一类边界条件。此外，对于隧洞衬砌结构的两个侧面，在温度场计算中均设为绝热的第二类边界条件。

在应力场的计算过程中，对于围岩和衬砌结构的对称面给予垂直于该表面的Z方向的水平位移约束，而围岩外围则设为全约束边界条件。当一次支护和二次衬砌的交界面被新的混凝土覆盖后，对流换热的第三类热学边界条件和力学条件都会消失。

2.3 计算方案

为了将掺加MgO的混凝土和普通混凝土的温度徐变应力情况进行比较，文中采用了两种计算方案，即在相同的计算工况下分别计算出长历时的素混凝土和MgO混凝土的温度徐变应力。

输水隧洞的计算工况采用先浇筑一次支护喷混凝土，然后在第14 d浇筑二次衬砌的混凝土底板。开始施工后的第42 d，即浇筑底板之后的第28 d开始浇筑二次衬砌的边顶拱部分。输水隧洞在施工后180 d开始通水进入运行阶段，通水水温5℃。混凝土浇筑的初始温度为25℃，整个仿真计算方案的持续时间为365 d。

2.4 有限元计算成果及分析

2.4.1 温度场计算分析

通过对输水隧洞温度场的分析计算，可以得到施工期及运行期间混凝土二次衬砌的温度分布情况和发展规律。考虑到隧洞衬砌属于对称结构，且混凝土产生水化热的温度变化过程比较相似，因此分别选取二次衬砌底板和边顶拱衬砌在中央断面的两个典型节点作为代表，如图4所示。混凝土二次衬砌边顶拱节点A以及底板节点B在365 d的温度历时曲线如图5所示。

由图5可以看出，在混凝土二次衬砌的施工阶段，隧洞衬砌的温度场经历了水化热温升和随环境温度产生整体温降这两个阶段。在温升阶段，混凝土由于水化热的作用使得二次衬砌的温度迅速升高，并且在24 h以内达到最高温度。其中，隧洞衬砌底板代表节点B在浇筑后的第0.5 d达到了最高温度29.5℃左右，边顶拱衬砌节点A在浇筑后的第0.4 d达到了最高温度28.8℃左右，二者的温升变化规律基本相同。边顶拱的最高温度发生在边顶拱端部的中央部位，底板衬砌的最高温度发生在拐角混凝土较厚的支承部位。混凝土浇筑后的温降阶段主要发生在最高温升后的7 d内，温降幅度达15℃。温降阶段结束后的混凝土温度基本维持在洞内环境温度15℃左右，并且趋于稳定。由于底板衬砌的厚度和边顶拱衬砌的厚度均为0.3 m，因此二者的最高温升峰值比较接近。

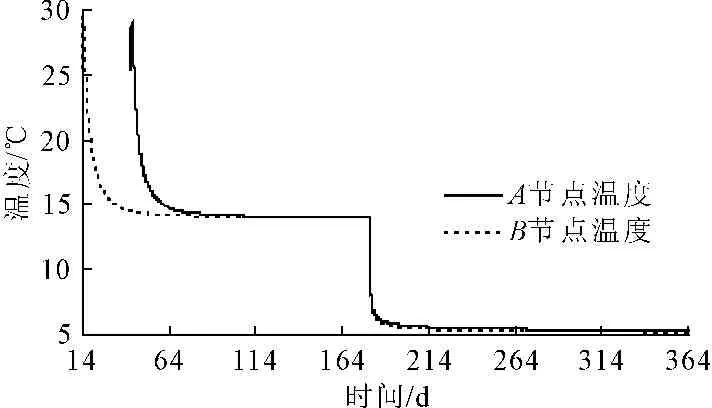
图4 隧洞边顶拱及底板典型点的选取

图5边顶拱及底板典型点温度历时曲线

隧洞混凝土衬砌开始浇筑180 d之后，输水隧洞开始通水并进入运行阶段。由于洞内水温较低，仅为5℃，且衬砌厚度较薄，因此二次衬砌混凝土受外界水温的影响较为明显。输水隧洞在通水后的4.5 d内衬砌温度迅速由14.0℃左右下降到6.1℃左右，之后再缓慢趋近于最低温度5℃。虽然整个运行阶段中衬砌混凝土仍存在有缓慢的水化热反应，但是对于衬砌整体的温度变化而言其影响已不再明显。

2.4.2 应力场计算分析

通过对应力场的计算成果进行分析比较，可以得出在不同的应力计算时刻，最大拉应力的分布情况也有所变化。这里分别选取边顶拱衬砌和底板衬砌的两个代表节点，即边顶拱代表节点C和衬砌底板代表节点B，然后分别对它们在施工阶段及运行阶段的应力发展过程变化曲线进行分析。在两种不同的计算方案下，代表节点的最大主应力变化过程曲线分别如图6和图7所示。

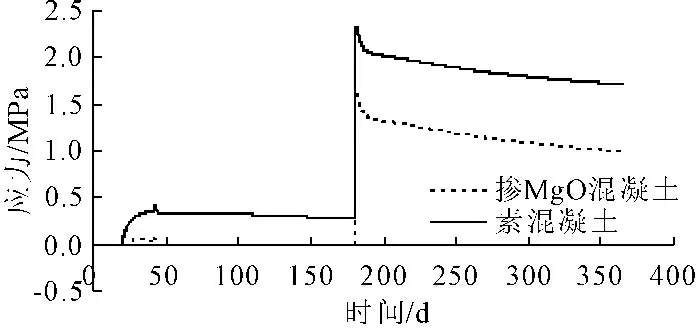
图6 衬砌底板节点B最大主应力S1对比图

图7衬砌边顶拱节点C最大主应力S1对比图

通过对隧洞衬砌应力场的计算结果进行分析可以看出，各个节点的温度徐变应力的变化过程和变化规律是相似的。在衬砌的施工阶段，混凝土一般经历了水化热温升带来的短暂压应力增长、温降初期的压应力减小、温降中后期的拉应力产生及增长直至趋于平稳这样一个发展过程。

在输水隧洞运行阶段，由于水温比较低，隧洞衬砌在水温冷却的作用下迅速产生收缩变形，从而抵消了水化热温升带来的膨胀效果，产生了较大的拉应力。在之后的运行期间，拉应力开始逐渐降低并趋于平稳。

从衬砌底板和边顶拱的应力情况对比来看，可以通过分析得到以下几点：

(1) 由于在浇筑边顶拱混凝土之前，先浇筑的底板衬砌已经接近外界环境温度，二者温差较大，因此在温降初期边顶拱衬砌的最大拉应力主要出现在靠近边顶拱的端部位置。

(2) 在素混凝土计算方案下，施工阶段衬砌底板节点B的最大主拉应力为0.419 MPa，发生在浇筑后的第28.3 d。边顶拱衬砌代表节点C的最大主拉应力为0.198 MPa，发生在浇筑后的第54.4 d。衬砌底板节点的最大主拉应力要明显高于边顶拱衬砌的最大主拉应力。

(3) 对于底板衬砌而言，在掺加MgO混凝土的计算方案下，底板衬砌节点B的最大主应力的变化规律和素混凝土计算方案基本是相同的。但是MgO混凝土计算方案下的最大主拉应力仅为0.074 MPa，比素混凝土计算方案下的0.419 MPa减小了82.34%；同样，对于混凝土边顶拱衬砌节点C，施工阶段掺加MgO的计算方案下所承受的应力值均为压应力，比素混凝土计算方案下的最大主拉应力减小了100.51%。

(4) 在输水隧洞的运行阶段，即隧洞混凝土衬砌开始浇筑的180 d之后，由于受到水温的影响和水压力的作用，混凝土迅速产生收缩变形并引起较大的拉应力。其中，掺加MgO混凝土方案下底板节点B的最大主拉应力为1.63 MPa，比素混凝土方案下的最大主拉应力值2.32 MPa减少了29.74%。同样对于边顶拱衬砌节点C，掺加MgO混凝土计算方案下的最大主拉应力值为1.28 MPa，比素混凝土方案下的2.04 MPa减少了37.25%。

(5) 由图6和图7中两种计算方案下的应力曲线对比可以看出，相比较素混凝土的施工方案，掺加MgO之后混凝土的主拉应力值要明显小于前者。这是因为混凝土在掺加MgO膨胀剂之后会产生一定的自生体积膨胀变形，从而在一定程度上抵消了由温降收缩变形引起的拉应力，甚至使得混凝土转变为受压状态。由此可见，在混凝土中掺加MgO膨胀剂是一种有效的防裂措施。