蜂窝梁-实腹柱十字形节点受力性能研究

聂少锋，朱纪钊，马 轶，叶梦娜，宋龙飞

(1. 长安大学 建筑工程学院，陕西 西安 710061； 2. 陕西省高速公路建设集团公司，陕西 西安 710054)

0引 言

蜂窝梁是由H型钢沿腹板以一定的折线或弧线切割形成的两部分错位焊接而成的新型钢构件形式。与原型钢相比，蜂窝构件自重较轻；采用蜂窝构件可以节省钢材，且便于贯穿管线，减小建筑高度，综合效益显著[1-3]。在蜂窝结构中，梁柱节点起着传递弯矩和剪力的作用，其性能直接影响着结构的强度、刚度和稳定性[4]。梁柱节点处应力集中、内力分布复杂，因此对蜂窝梁柱节点的受力性能开展研究是推广应用蜂窝结构亟待解决的问题。

国内外学者已对蜂窝节点进行了部分研究。Zaarour等[5]对12根蜂窝梁进行试验研究，采用有限元软件预测屈曲载荷，并提出图表法及有限差分法计算屈曲荷载。周朝阳等[6]通过对六边形孔和圆孔蜂窝梁进行大量有限元分析，得到腹板刚度折减系数表，并给出该系数的半理论半经验计算公式，采用该公式可快速求解蜂窝梁的等效抗弯刚度。张艳霞等[7]对蜂窝钢框架边节点的受力性能进行有限元分析，研究表明通过调整梁上孔洞大小和间距可以改善蜂窝节点的抗震性能。贾连光等[8-9]对蜂窝式钢框架边节点进行了低周反复荷载试验研究和有限元分析，结果表明蜂窝节点滞回曲线饱满，耗能能力较好，相比于柱上开孔位置，梁上开孔位置对节点抗震性能影响更显著；文献[9]提出了梁上第1个孔洞距柱翼缘距离取值的建议公式。张德刚等[10]对狗骨-蜂窝式梁柱节点进行了梁端循环位移荷载作用下的有限元分析，研究表明狗骨-蜂窝式节点滞回曲线饱满，延性和耗能能力强，塑性变形能力良好。王培军等[11]对跨中集中力作用下圆角多边形孔蜂窝梁进行有限元分析，研究其腹板的屈曲模式和屈曲承载力，提出可用于计算相邻孔间腹板屈曲承载力的改进斜压柱理论模型。Wang等[12]采用有限元分析方法研究影响钢桁架蜂窝梁腹杆纵向剪切屈曲强度的因素，提出了腹杆竖向剪切屈曲强度的设计方程。李明等[13]对24个不同钢材屈服强度和含钢率的蜂窝节点进行有限元分析，结果表明开孔率对该类节点抗震性能影响最大，孔间距影响最小。Budi等[14]对六边形孔蜂窝钢梁的开孔角度及孔距进行了试验与有限元分析结合的优化研究，结果表明蜂窝钢梁最佳孔角为60°，最佳孔距为孔高的18.6%～26.6%。

已有研究大多针对蜂窝式钢框架、蜂窝式钢框架梁柱边节点，且加载方式多为梁端加载，无法考虑荷载-位移(P-Δ)效应，这与节点的实际受力状况存在差异。为研究蜂窝梁-实腹柱节点的真实受力状态，本文采用柱端加载模拟分析蜂窝梁-实腹柱十字形节点在框架中的受力情况，通过ABAQUS有限元软件建立蜂窝梁-实腹柱十字形节点有限元模型，在与已有试验结果对比分析验证有限元模型正确性的基础上，详细研究蜂窝梁的扩高比K与开孔位置L等因素对蜂窝梁-实腹柱十字形节点受力性能的影响。

1蜂窝梁-实腹柱节点设计

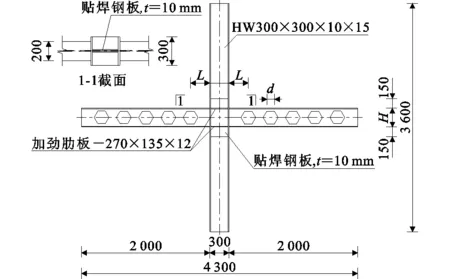
图1节点构造及尺寸(单位：mm)Fig.1Structure and Dimension of Joint (Unit:mm)

蜂窝梁-实腹柱节点设计如下：蜂窝梁长2 m，由原始型号为HW200×200×8×12的型钢加工而成，孔洞为正六边形孔；柱高3.6 m，柱截面型号为HW300×300×10×15，无孔洞；加劲肋板的尺寸为-270 mm×135 mm×12 mm。节点设计参照《钢结构设计规范》(GB 50017—2003)[15]和《建筑抗震设计规范》(GB 50011—2010)[16]中有关构造规定，柱腹板厚度未满足文献[15],[16]对节点域柱腹板厚度的要求，故加设补强板，补强板厚度为10 mm，贴焊于节点域柱腹板两侧，上下两端分别伸出梁翼缘各150 mm；蜂窝梁孔洞大小及位置参照文献[9]相关取值。蜂窝梁-实腹柱节点形式及构件尺寸见图1，其中H为蜂窝梁高，d为孔边长，t为贴焊钢板厚度。经验算，节点满足文献[15],[16]对于节点域承载力的要求，同时满足“强柱弱梁、强节点弱构件”的抗震设计要求。

蜂窝梁的扩高比K为蜂窝梁扩高后截面高度H与原型钢截面高度h之比，即K=H/h；梁上第1个孔洞中心距柱翼缘的距离为L。参照文献[17]的建议取值，L应大于H。蜂窝梁扩高后所对应的梁高和孔边长以及有限元分析模型节点参数范围见表1，同时与未经扩高及开孔的原型钢梁柱节点进行对比分析。

表1蜂窝梁及节点参数范围Tab.1Parameter Ranges of Castellated Beams and Joints

2有限元模型的建立

2.1本构关系与网格划分

蜂窝梁-实腹柱节点各部件采用非协调实体单元(C3D8I)。梁柱连接采用全焊接刚性连接，梁翼缘与柱翼缘采用对接焊缝连接，梁腹板与柱翼缘采用角焊缝连接，设计为焊缝与母材等强。采用Tie命令模拟焊缝连接，有限元建模时忽略构件的初始缺陷、焊缝缺陷以及焊接残余应力对节点性能的影响，考虑几何非线性。网格划分时，对节点域附近以及六边形蜂窝孔洞四周网格进行加密处理，如图2所示。

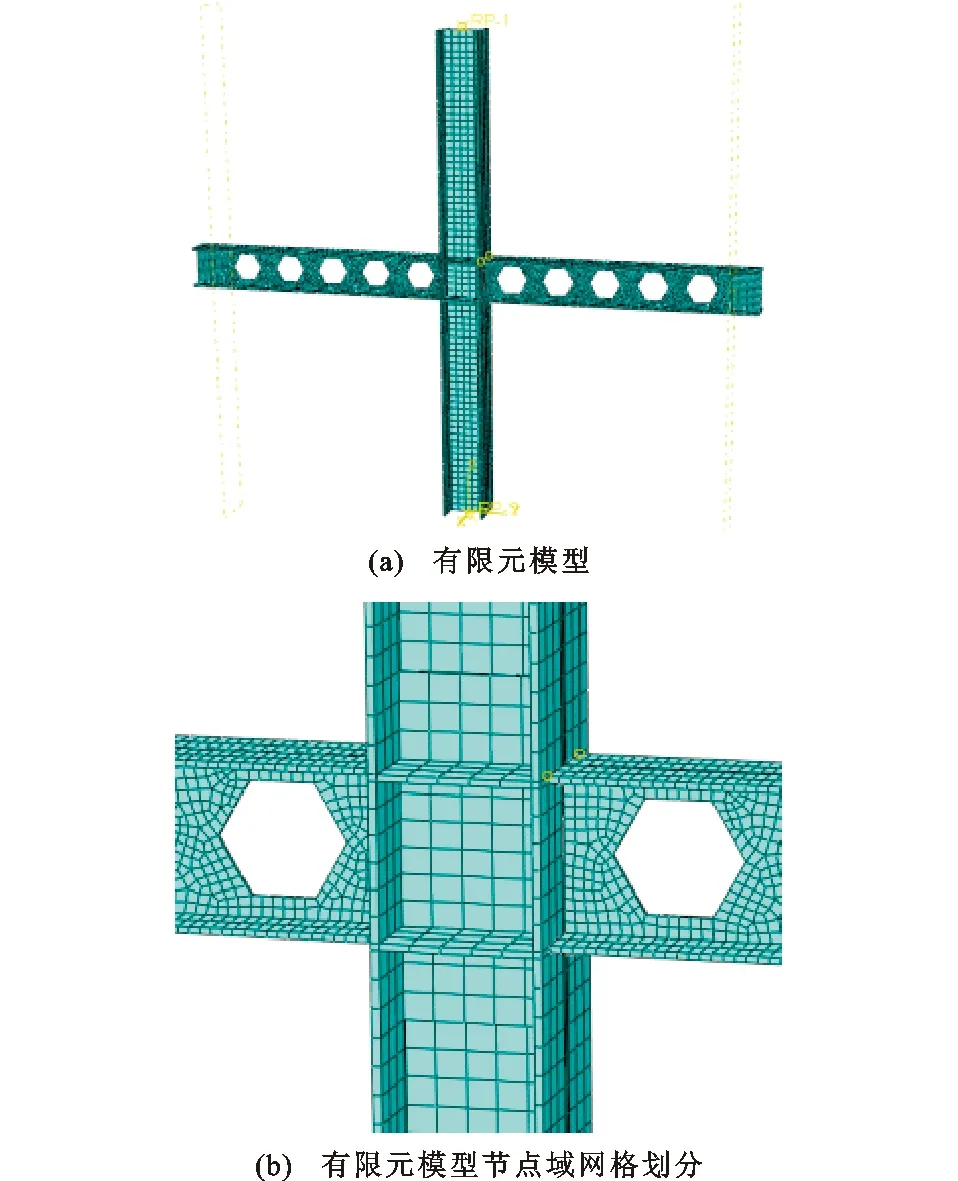
图2有限元模型的网格划分Fig.2Mesh Generation of Finite Element Model

钢材选用Q235B钢，采用三折线本构模型，如图3所示，其中σy，σu分别为钢材屈服强度和极限强度，σ，ε分别为应力、应变，εy，εu，εst分别为钢材屈服应变、极限应变和破坏应变；参考文献[18],[19]中不同厚度钢材力学性能试验结果，取泊松比为0.3，材性指标见表2。

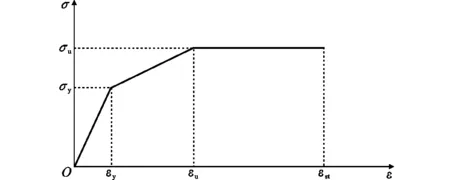
图3钢材应力-应变曲线Fig.3Stress-strain Curve of Steel

构件厚度t/mm屈服强度σy/MPa极限强度σu/MPa弹性模量E/105 MPa柱腹板10278.70460.542.06柱翼缘15253.13472.072.09梁腹板8255.56395.832.04梁翼缘12268.98420.372.02肋板12268.98420.372.02补强板10278.70460.542.06

2.2加载制度与边界约束条件

为真实模拟梁柱节点在钢框架中的实际受力情况，并考虑P-Δ效应，有限元节点采用柱顶水平单调加载的方式。为避免柱端应力集中现象，在柱顶和柱底分别设置参考点并与端面耦合。分别建立2个分析步，在Step-1中，对柱顶参考点施加竖向荷载N=650 kN，轴压比为0.25；在Step-2中，对柱顶参考点施加水平位移荷载。有限元模型中，柱顶在平面内为自由端，约束柱顶X方向位移和Y，Z方向转动以模拟平面外支撑；柱底为铰接，约束柱底X，Y，Z三个方向位移和Y，Z方向转动；梁端为单链杆连接，约束梁端X，Z方向位移和Y，Z方向转动；加载方式及边界约束条件见图4。

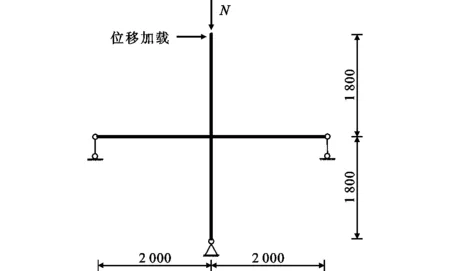
图4加载方式及边界约束条件(单位：mm)Fig.4Loading Method and Boundary Constraint Condition (Unit:mm)

2.3有限元分析结果验证

为验证本文有限元模型的准确性及适用性，选取文献[8]中具有代表性的蜂窝节点FWJD-2(梁上第1个开孔中心距柱翼缘距离L=430 mm；柱上第1个开孔中心距梁翼缘距离e=335 mm)、FWJD-3(L=130 mm，e=335 mm)进行有限元模型的验证。试件梁截面型号为H150×100×6×8，孔边长为58 mm；柱截面型号为H186×125×6×8，孔边长为70 mm。试验试件构造及尺寸见图5。有限元验证时材性与试验材性保持一致，试验与有限元分析结果对比见图6。

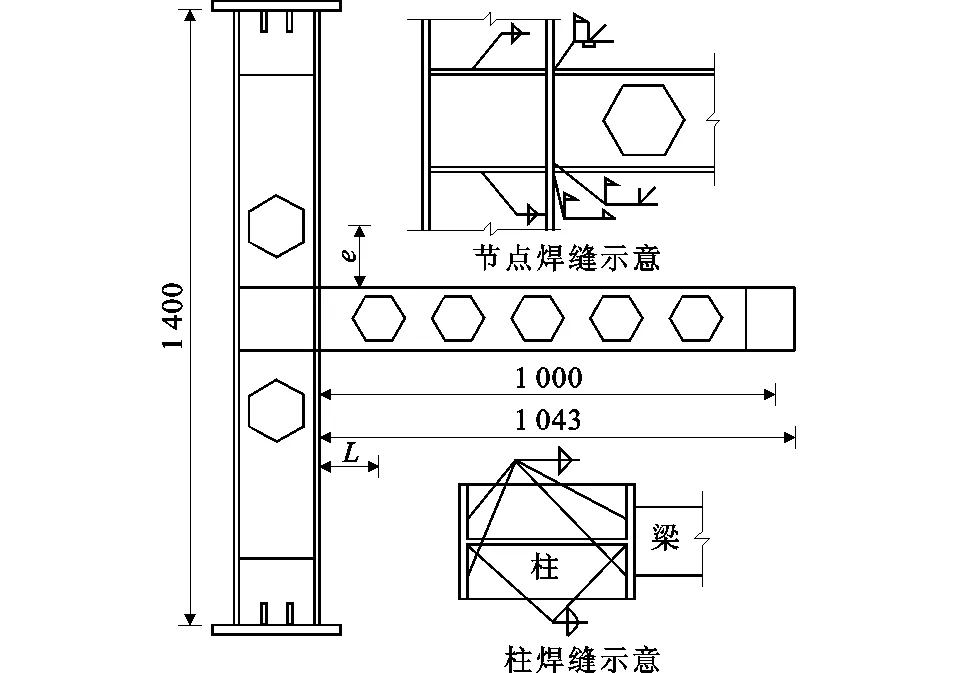
图5试件构造及尺寸(单位：mm)Fig.5Structure and Dimension of Specimen (Unit:mm)

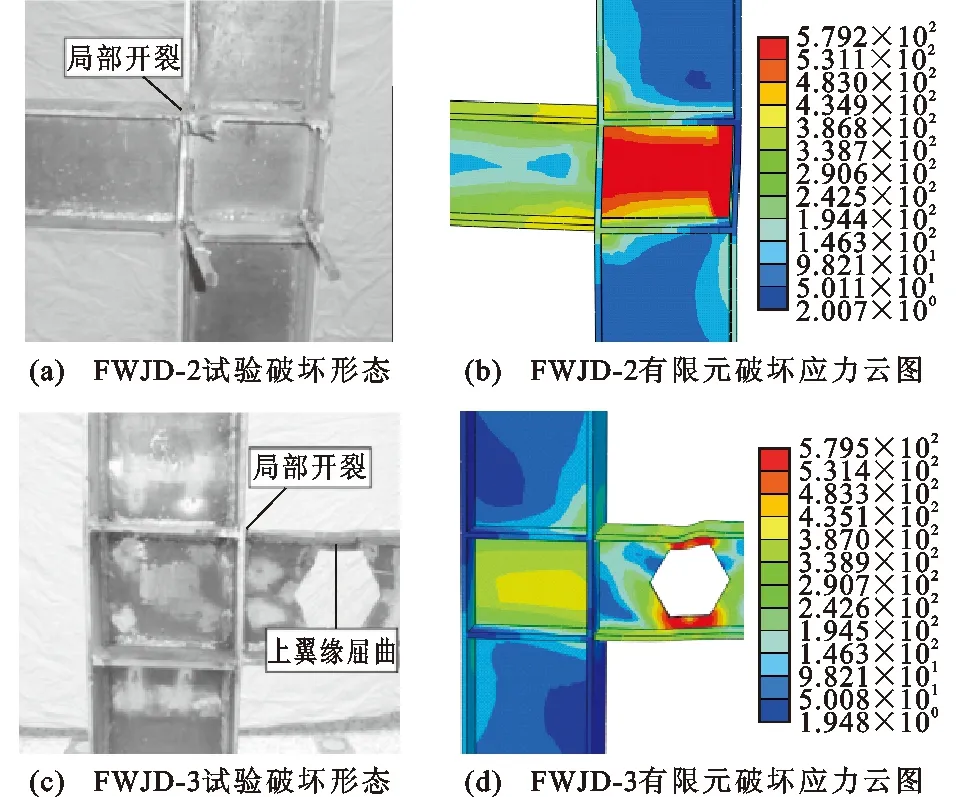
图6试验与有限元结果对比(单位:MPa)Fig.6Comparison Between Experimental and Finite Element Results (Unit:MPa)

由图6可知：试验与有限元分析得出的破坏模式基本一致，FWJD-2梁端应力集中，节点域产生明显剪切变形；FWJD-3梁上第1个孔洞的上下孔角以及所对应的上翼缘屈曲，节点域未出现明显的变形。由Von Mises应力云图可以看出，有限元模型中FWJD-2破坏时表现为节点域柱腹板屈服；FWJD-3破坏时表现为应力集中位置出现在梁上第1个孔洞上下孔角处，并形成明显的塑性铰，与试验结果保持一致。

通过试验与有限元分析得到的荷载-位移滞回曲线对比见图7。由图7可知：试验与有限元所得滞回曲线吻合较好，FWJD-2有限元模拟最大荷载为55.33 kN，试验值为58.76 kN，最大相对误差为6%；FWJD-3有限元模拟最大荷载为46.68 kN，试验值为49.67 kN，最大相对误差为6%。试验结果和有限元分析结果的节点刚度以及滞回环面积基本一致，表明所建立的有限元分析模型是正确的，具有较高的精度。

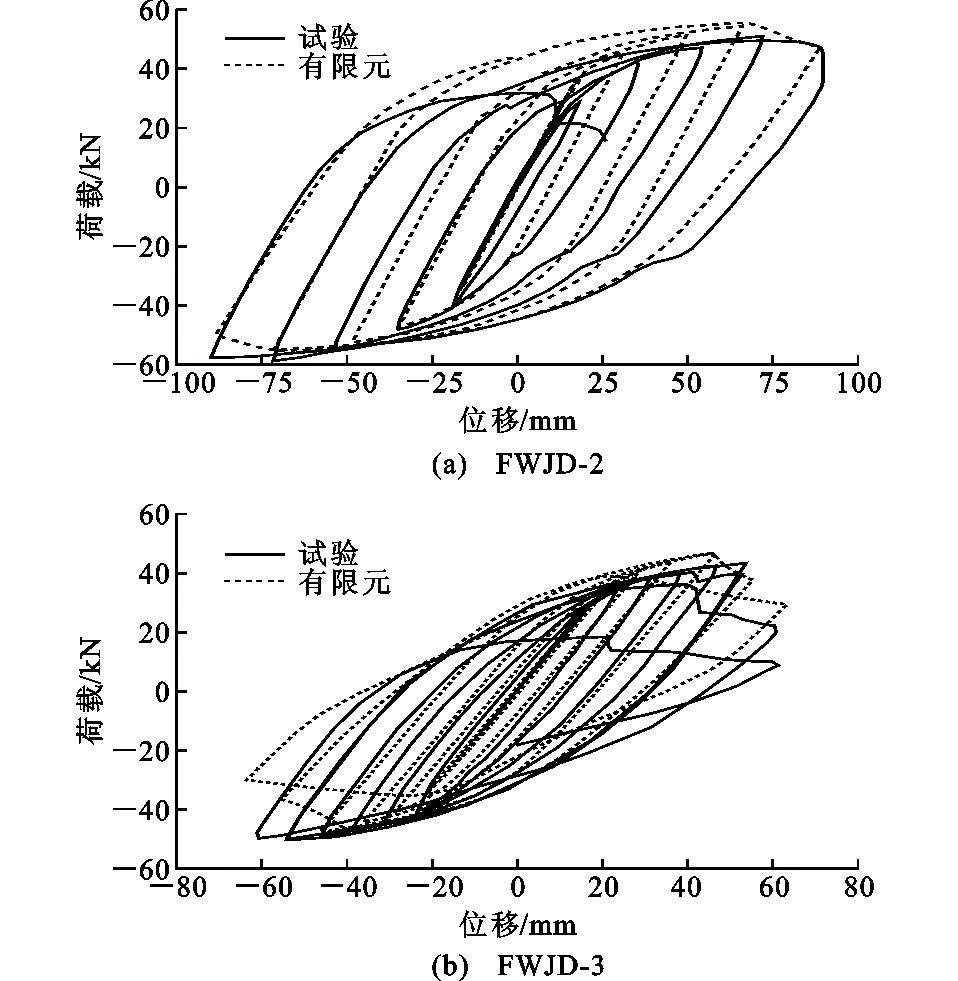
图7试验与有限元荷载-位移滞回曲线对比Fig.7Comparisons Between Experimental and Finite Element Load-displacement Hysteresis Curves

3蜂窝梁-实腹柱节点受力性能分析

3.1蜂窝梁-实腹柱节点破坏形态和塑性铰位置

对表1中不同扩高比所对应模型参数范围进行有限元分析，研究蜂窝梁-实腹柱节点在柱顶水平单调荷载作用下的最大承载力以及破坏形态。各蜂窝梁-实腹柱节点最大承载力见表3，其中原型钢梁柱节点(未开蜂窝孔洞)最大承载力为72.23 kN；图8为原型钢梁柱节点和当L=300 mm时，不同扩高比K以及当K=1.4时，梁上开孔位置不同的蜂窝梁-实腹柱节点破坏模式及Von Mises应力云图。

表3蜂窝梁-实腹柱节点最大承载力Tab.3Maximum Bearing Capacity of Castellated Beam-solid Column Joints

图8典型试件破坏模式及应力云图(单位：MPa)Fig.8Failure Modes and Stress Nephograms of Typical Specimens (Unit:MPa)

对比分析图8可知：当蜂窝梁的扩高比以及梁上第1个孔洞位置不同时，蜂窝梁-实腹柱节点破坏时表现为截然不同的破坏形态；当扩高比较小或孔洞位置距离节点域较远时，节点破坏模式为梁端应力集中，节点域产生明显剪切变形，与原型钢节点破坏模式相似；当扩高比和孔洞位置选择合适时，蜂窝梁-实腹柱节点在水平荷载作用下的破坏位置将出现在第1个孔洞附近，使塑性铰由节点域外移，从而具有较好的静力性能以及抗震性能。因此，本文所选的2个参数扩高比K以及梁上第1个孔洞中心距柱翼缘的距离L对此类蜂窝节点的受力性能影响很大，以下结合图8分别分析2个参数对蜂窝梁-实腹柱节点承载力造成的影响。

3.2扩高比对蜂窝梁-实腹柱节点承载力和塑性铰位置的影响

图9不同扩高比时节点荷载-位移曲线对比Fig.9Comparisons of Load-displacement Curves of Joints with Different Expansion Ratios

图9为L=300，400，500，600 mm和不同扩高比时蜂窝梁-实腹柱节点在水平荷载作用下的荷载-位移曲线。由图9可知：当梁上第1个孔洞中心距柱翼缘的距离L不变时，蜂窝梁-实腹柱节点在水平荷载下承载力随扩高比K的变化趋势是一致的，即随着K的增加，承载力先增加后降低，并在K=1.4左右时达到峰值。这是由于扩高比较小时，提高梁高对蜂窝梁抗弯承载力的贡献大于开孔对其造成的削弱作用，而扩高比大于1.5时，梁上开孔造成的削弱作用过大，使其抗弯承载力大幅降低。当K从1.3增大至1.4时，最大承载力增长5.7%；当K从1.4增大至1.5，从1.5增大至1.6，从1.6增大至1.7，最大承载力分别降低14.7%，29.3%，36.1%。可见，当K=1.3～1.5时，梁上蜂窝孔洞对蜂窝梁-实腹柱节点水平承载力影响较小，其中K=1.4为此类节点最佳扩高比；当K>1.5时，节点水平承载力降幅过大，不利于此类节点的应用。

另外，扩高比会对塑性铰出现的位置产生较大影响。由图8(b)～(d)可知，L=300 mm不变，当K=1.3时，节点破坏时节点域先屈服，梁端和孔洞区应力均较大，与原型钢梁柱节点破坏模式类似，这是由于蜂窝梁腹板开孔造成的削弱不足以使塑性铰节点域外移，无法满足“强柱弱梁、强节点弱构件”的设计原则；当K=1.4，1.5时，蜂窝梁第1个孔洞处抗弯承载力小于梁端抗弯承载力，塑性铰远离梁端区域，出现在第1个孔洞处，从而避免在节点域破坏。

3.3开孔位置对蜂窝梁-实腹柱节点承载力和塑性铰位置的影响

图10为扩高比K分别为1.4，1.5时，不同开孔位置的蜂窝梁-实腹柱节点在水平荷载作用下的荷载-位移曲线。由图10可知：当扩高比不变时，随着梁上第1个孔洞中心距柱翼缘的距离L增大，蜂窝梁-实腹柱节点水平承载力先增加后趋于稳定，这是由于孔洞距节点域越远，对节点的影响越小，距离超过一定范围后，对节点域附近削弱作用消失，故节点水平承载力趋于稳定。

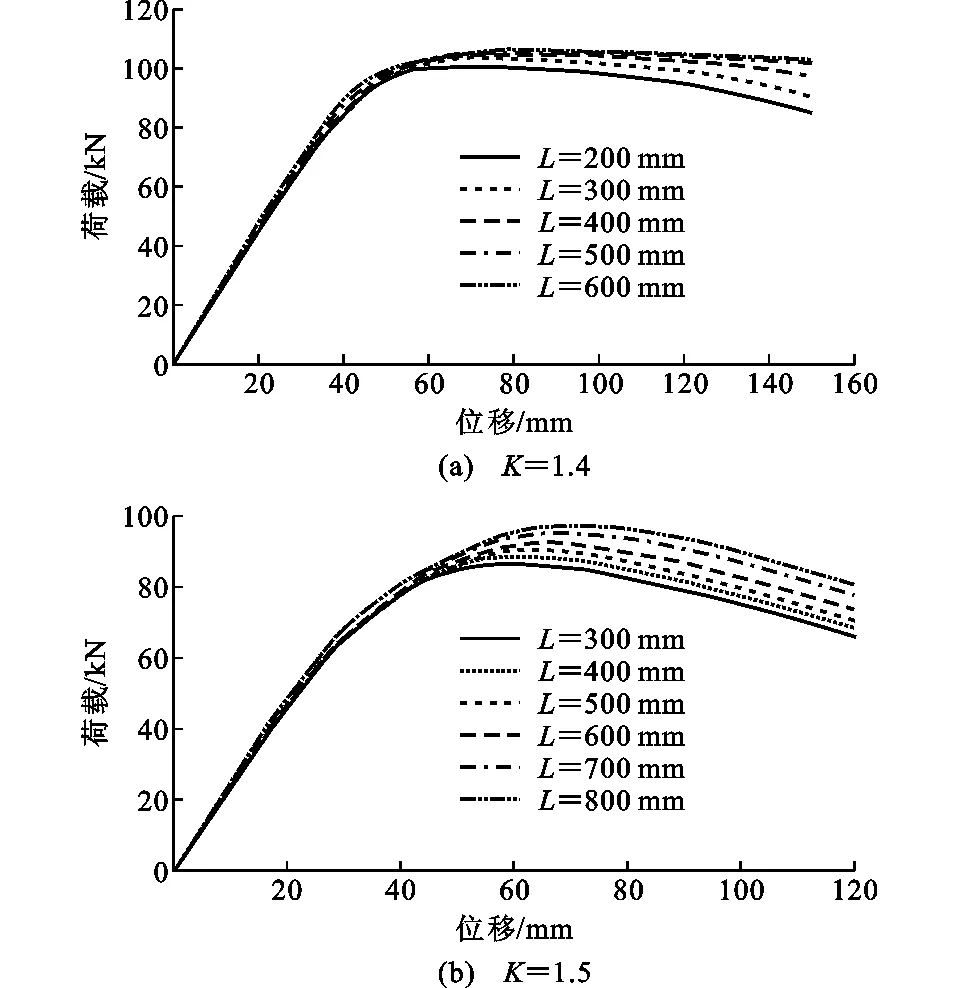
图10不同开孔位置节点荷载-位移曲线对比Fig.10Comparisons of Load-displacement Curves of Joints with Different Locations of Holes

开孔位置也会对塑性铰出现位置造成影响。由图8(c)，(e)，(f)可知：扩高比K=1.4不变，当L=200 mm时，开孔位置与节点域较近，塑性铰在孔洞附近形成后迅速向节点域发展，故开孔对塑性铰外移的影响不够明显；当L=300 mm时，塑性铰出现在梁上第1个孔洞中心；当L=500 mm时，开孔位置距节点域距离较远，节点域先于孔洞处出现塑性铰，塑性铰外移影响同样不明显。

3.4蜂窝梁-实腹柱节点的扩高比和开孔位置建议取值

综合考虑扩高比和开孔位置对蜂窝式梁柱节点塑性铰产生位置的影响，表4为同时考虑2组参数情况下，各蜂窝梁-实腹柱节点塑性铰出现位置距柱翼缘的距离。定义塑性铰出现在节点域时，距柱翼缘距离为0；塑性铰出现在孔洞附近时，距柱翼缘距离为L。由表4可知：当扩高比K=1.3时，梁上开孔对塑性铰出现位置影响较小；当K=1.4且开孔位置合理时，梁上塑性铰将外移至开孔处；当K>1.4时，孔洞较大，均可控制塑性铰出现在孔洞处。综合考虑图9所示不同扩高比的蜂窝梁-实腹柱节点在水平荷载作用下的荷载-位移曲线，当K>1.5时，节点水平承载力降幅过大，不利于此类节点的应用。综上所述，蜂窝梁-实腹柱节点扩高比K建议取值为1.4～1.5。

对于开孔位置，为综合考虑原型钢尺寸所带来的影响，定义参数αh为

αh=L/h

(1)

式中：h取为200 mm。

根据表4结果得出αh建议取值，见表5：当K=1.4时，αh建议取值为1.5～2.5；当K=1.5时，αh建议取值为1.5～4.0。

4蜂窝梁-实腹柱节点抗震性能分析

4.1滞回曲线与骨架曲线

为分析上述建议取值范围内蜂窝梁-实腹柱节点的抗震性能，对K=1.4，L=400 mm的蜂窝梁-实腹柱节点(JD-1)，与K=1.4蜂窝梁等高的实腹式梁柱节点(JD-2)，以及原型钢梁柱节点(JD-3)进行低周反复荷载作用下的抗震性能对比分析。加载制度如下：采用位移控制加载，构件屈服前每级增幅为0.25Δy(Δy为屈服位移)，构件屈服后每级增幅为Δy，每级循环1圈，当荷载下降到峰值荷载的85%时停止加载。屈服位移Δy采用通用屈服弯矩法确定[20]。图11为3种节点柱顶的P-Δ滞回曲线和骨架曲线。由图11(a)可知：蜂窝梁-实腹柱节点JD-1与梁上未开孔的实腹式梁柱节点JD-2在低周反复荷载作用下的P-Δ滞回曲线均非常饱满，具有良好的耗能能力，说明在参数设置合理的情况下，蜂窝梁-实腹柱节点的抗震性能并未因开蜂窝孔洞而削弱；蜂窝梁-实腹柱节点和实腹式梁柱节点因梁高增大，其最大承载力以及滞回环面积均显著大于原型钢梁柱节点JD-3。

表5αh建议取值Tab.5Proposed Values of αh

图11P-Δ滞回曲线与骨架曲线对比分析Fig.11Comparisons of P-Δ Hysteresis Curves and Skeleton Curves

由图11(b)可知：加载初期，蜂窝梁-实腹柱节点与实腹式梁柱节点初始刚度相近，且均高于原型钢梁柱节点；加载中后期，蜂窝梁-实腹柱节点梁上开孔处屈服，刚度下降显著，蜂窝梁-实腹柱节点与实腹式梁柱节点骨架曲线峰值点均大于原型钢梁柱节点，具有较高的承载力。

4.2节点延性分析

采用延性系数μ来衡量梁柱节点的延性，延性系数为节点极限位移与屈服位移之比。节点JD-1，JD-2，JD-3的延性系数见表6。由表6可知：蜂窝梁-实腹柱节点的延性系数低于实腹式梁柱节点，与原型钢梁柱节点相差不大，表明梁上孔洞对节点延性削弱较小，蜂窝梁-实腹柱节点具有良好的延性。

表6节点延性系数与等效黏滞阻尼系数Tab.6Ductility Coefficients and Equivalent Viscous Damping Coefficients of Joints

4.3节点耗能能力

采用等效黏滞阻尼系数he来衡量节点的耗能能力[21]，等效黏滞阻尼系数计算示意图如图12所示，其值按下式计算

(2)

式中：SFBEDF为曲线FBEDF围成的面积；S△AOB，S△COD分别为△AOB，△COD的面积。

图12等效黏滞阻尼系数计算示意图Fig.12Calculation Schematic of Equivalent Viscous Damping Coefficient

节点JD-1，JD-2，JD-3的等效黏滞阻尼系数见表6。由表6可知：蜂窝梁-实腹柱节点的等效黏滞阻尼系数较实腹式梁柱节点和原型钢梁柱节点分别提高41.7%和27.5%，表明蜂窝梁-实腹柱节点具有良好的耗能能力与抗震性能。

5结语

(1)蜂窝梁-实腹柱十字形节点由于扩高，其抗弯刚度和抗弯承载力较原型钢梁柱节点均有较大幅度的提高，且可以利用梁上开孔的削弱作用，使塑性铰由节点域向第1个孔洞处转移，避免在节点域破坏，满足“强节点弱构件”的抗震设计要求。

(2)扩高比K和梁上第1个孔洞中心距柱翼缘的距离L是影响蜂窝梁-实腹柱十字形节点受力性能及塑性铰位置的重要参数。当K=1.3～1.5时，梁上蜂窝孔洞对节点水平承载力削减作用较小，其中K=1.4为最佳扩高比；当K>1.5时，节点水平承载力降幅过大，不利于此类节点的应用。

(3)综合考虑扩高比和开孔位置2组参数的影响，定义参数αh=L/h，本文建议参数取值范围如下：K建议取值为1.4～1.5；当K取1.4时，αh建议取值为1.5～2.5，当K取1.5时，αh建议取值为1.5～4.0。在此参数范围内，蜂窝梁-实腹柱十字形节点滞回曲线饱满，延性与耗能能力良好，具有良好的抗震性能。