基于时空域与频域融合的农村变电站中运动目标检测算法

刘一凡,蔡振江※,司永胜

（1.河北农业大学机电工程学院，保定 071000；2. 河北农业大学信息科学与技术学院，保定 071000）

0 引 言

中国农村变电站通常规模比较大，电气设备都比较传统，设备自动化和智能化程度普遍较低，因此在变电站的日常运行维护中对人力资源的要求相对较高[1-2]。在农村变电站日常巡检与突发故障检修时，都需要工作人员进入现场操作。变电站存在大量高危电气设备，为了保证工作人员的安全与变电站的正常运转，通常要求工作人员在变电站现场特定的安全（检修）区域内工作。为了避免出现工作人员离开安全（检修）区域的情况，需要对在场的工作人员（即运动目标）实时监测。

目前运动目标的智能识别与定位在安全监控领域有着日益广泛的研究与应用[3-6]。本文结合中国农村变电站电气设备比较传统、设备自动化和智能化程度普遍较低特点，采取一种在变电站现场特定的安全（检修）区域周围即时架设相机的方法对工作人员实时监控，从而实现站内工作人员监测的远程化、智能化、自动化，使工作人员的安全性大大提高。其中运动目标的检测是视频监测关键步骤。目前常见的运动目标检测算法主要有：背景差分法、帧间差分法、主成分分析法、自适应背景建模算法等。这些检测算法应用在变电站运动目标检测中存在背景去除较差、目标信息保留不完整的问题。

背景差分法[7-8]在大部分实际应用中，背景信息极易受到光照变化、目标阴影以及一些目标之外的杂质与噪声的影响，不适用于变电站户外监测。帧间差分法[9-12]通常无法提取出目标的完整信息，且在目标运动过慢或者过快的情况下，会出现目标丢失或者误检测为2个目标的情况，不适用于监测变电站内不同活动状态下的工作人员。

近年来，鲁棒性主成分分析法（robust principal component analysis，RPCA）受到了广泛关注与研究[13-14]。目前主要包括：1）基于最小化迭代算法完成快速主成分寻踪（fast principal component pursuit，FPCP）[15-16]。该算法对于背景动态变化的情况检测效果不佳。2）基于格拉斯曼流形（Grassman manifold）的自适应子空间跟踪算法（Grassmannian robust adaptive subspace tracking algorithm，GRASTA）[17]，该算法去除背景效果良好，但运动目标信息保留不完整。

自适应背景建模算法应用广泛的主要有以下2种：1）混合高斯模型（Gaussian mixture model，GMM）算法[18-22]，该算法可以较完整地提取了运动目标信息，且去除了大部分背景噪声；2）视觉背景提取（Visual background extractor，ViBe）算法[23-25]，该算法计算复杂度略低于混合高斯模型算法，具有一定的鲁棒性和实时性。2种算法都存在一些共性缺点：如会在背景产生ghost鬼影现象；对于背景中的高频扰动噪声抑制效果较差；自适应更新的背景模型存在一定程度的滞后性，即检测到的背景噪声，可能需要 10帧甚至更多才能将噪声完全去除，影响变电站监测效率与精度。

针对上述不同算法在农村变电站运动目标监测上存在的问题，本文提出了一种多域融合（时域空域与频域）的农村变电站运动目标检测（time-domain space-domain and frequency- domain fusion，TSFF）算法。TSFF算法首先将传统的 2帧时域运算扩展为连续多帧的时域运算。并选取多帧图像相同位置处的像素值作为一组时域信号，通过短时傅里叶变换[26-28]对该信号作时频分析，并结合每帧图像上目标像素点的水平与垂直 4个方向上扩展邻域的像素点（空域），依次通过短时傅里叶变换作时频分析，将目标点与扩展邻域的视频幅值的标准差均值结合分析，通过设定双阈值，最终判断出目标点是否为背景、扰动噪声或运动目标。

1 常见运动目标检测算法原理

在常见的运动目标检测算法中，通常都是两帧之间在相同目标点位置作差值运算，只考虑到时域变化。如背景差分法与帧间差分法的本质都是计算不同帧图像同一像素位置在时域上像素值变化情况；自适应背景建模算法本质是计算生成背景模型，并与含有运动目标图像帧在时域上作差。其原理可表示为：

式中 m (i , j,n)表示第 n帧图像 ( i, j)位置处像素值；m(i , j,k)表示第k帧图像 ( i, j)位置处像素值，当k为n的相邻帧则为帧间差分法，当k为背景帧则为背景差分法； d ( i,j)表示2帧图像在 ( i , j)位置的像素差分值。

接着将像素差分值与设定阈值T作比较，小于该阈值则为静态背景，大于该阈值则为运动目标，最终完成整幅差分图像的二值化处理。有公式:

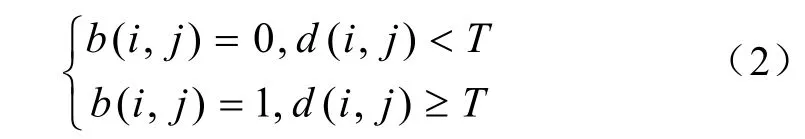
式中 ),(jib 表示差分图像中 ),( ji 位置的像素值，该值为1则为运动目标，该值为0则为静态背景。

2 TSFF算法检测原理

TSFF算法首先在时域上选取连续多帧图像，并在每帧图像相同位置处选取像素点构成一组时域信号，对该信号作短时傅里叶变换（short time Fourier transform，STFT），转换到频域观察信号幅值波动情况，并在每帧图像目标点水平与垂直4个方向上扩展邻域内（空域）各选取2个像素点，分别通过短时傅里叶变换完成时频分析，最终通过设定双阈值判断该像素点的信号特征。具体算法如下：

首先在时域上选取n帧连续图像构成一组三维时空图像组 M。在每帧图像的 ),( ji 位置处选取像素点，构成一组时域空间上的n维向量。该向量可表示为

式中 M ( i,j)表示n帧图像 ( i , j)位置的n维像素序列。

M ( i,j)可以看成是一组目标点像素值随时间变化的时域信号向量。本文采用短时傅里叶变换对时域信号向量进行时频变换。短时傅里叶变换。相较于基于全局处理的传统傅里叶变换，加入了一个时频局部化的窗函数，可以有效地分析一组时域信号在不同时刻的功率谱。所以短时傅里叶变换可以看作是移动窗口内依次对信号作傅里叶变换，可表示为

式中 )(uz 为输入信号； )(tg 为窗函数；f为短时傅里叶变换频率，由计算傅里叶变换的采样点数决定；t为短时傅里叶变换的时间，由输入信号的长度与窗函数的宽度决定；STFT(t,f)为短时傅里叶变换时频幅值，该值由一个 f行t列的矩阵构成。

窗函数 )(tg 选取与参数设定也十分关键。目前常用的窗函数主要包括矩形窗、海明窗与汉宁窗。其中，海明窗在频率范围中的分辨率较高，且能量聚集性强，旁瓣幅度较小，计算也比较简单，因此本文选择海明窗完成信号处理，有公式

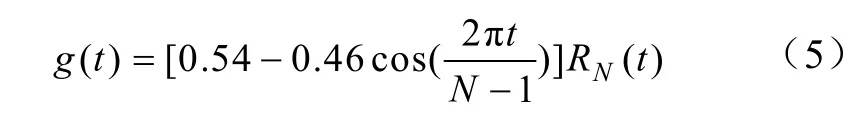
式中N为窗函数的宽度，也称窗长； RN(t)为矩形窗函数。

就本文需要处理的连续多帧时域向量而言，z ( u)即为式（3）中的 M ( i,j)。结合多帧图像中目标点信号特征，可以将多帧中像素值变化不大的背景点看作平稳信号；将多帧中像素值变化较大的运动目标或高频噪声点看作冲击信号。对于平稳信号，通过短时傅里叶变换得到的三维频谱图表现平稳，没有明显的波峰与波谷；对于冲击信号，通过短时傅里叶变换得到的三维频谱图表现波形变化明显，通常有波峰或波谷。所以本文通过计算时-频域上短时傅里叶变换时频幅值Sft( i,j)= STFT(t,f)的均值与标准差并设定阈值来判别信号特征。有公式

式中 ),( jiaf表示目标点 ),(jiM 在每段频率下不同时间短时傅里叶变换时频幅值的均值； bf( i,j)表示目标点M ( i ,j)在每段频率下不同时间短时傅里叶变换时频幅值的标准差； Cm表示目标点 M ( i,j)在每段频率幅值标准差的均值。对于平稳信号，计算得到标准差的均值 Cm很小，对于冲击信号，计算得到标准差的均值 Cm较大。所以本文通过设定阈值 T1首先检测出连续多帧图像中不同像素位置为平稳信号或冲击信号。有公式

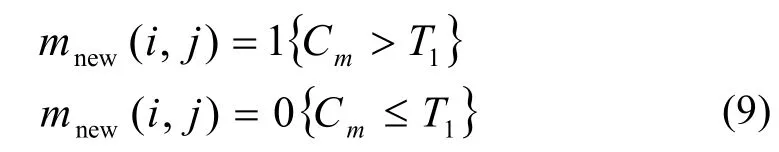
式中 mnew( i,j)表示 ( i , j)位置处新生成像素值，标准差的均值 Cm大于阈值 T1像素值为1（白色），反之像素值为0（黑色），生成二值分割图像。

通过式（9）可以判断出目标点为平稳信号或冲击信号。但是冲击信号可能是目标运动目标，也可能是背景扰动噪声。且当运动目标邻域像素值相差不大时导致其时频幅值波动较小，将其误检测为平稳信号。极易出现帧间差分法中运动目标出现的“空洞”现象。针对上述问题，本文在时频运算的基础上融合了空域运算，提出在每帧（空域）内结合目标点扩展邻域像素信息综合判断，进一步降低目标点误识别的概率。通常情况下，视频帧中的高频噪声分布区域零散，像素面积小，而运动目标通常分布区域集中且像素面积较大。所以本文通过结合目标点扩展邻域像素点在时频域的短时傅里叶变换进一步判断目标点的信号特征。为了保证在空域内获取足够像素信息判断目标点的运动情况，同时最大程度减少数据运算量，本文在每帧图像（空域）上目标点的水平与垂直4个方向上扩展邻域内各选取2个最外侧像素点。有公式

式中nh为第n帧图像中水平方向上扩展邻域2个最外侧像素点序列；nl为第n帧图像中垂直方向上扩展邻域2个最外侧像素点序列。

图1以5帧视频图像为例，展示了TSFF算法在时-空域选取像素点的情况。

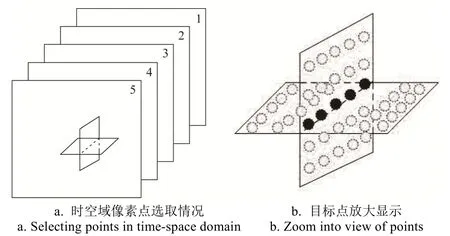
图1 连续5帧图像的像素点Fig.1 Selected pixels of five consecutive video frames

图1a为 TSFF算法在时-空域选取像素点在连续5帧图像中的某一位置示意图；图 1b为选取像素点的放大显示。图中深色圆点表示在5帧图像中目标点 m (i , j)的位置。白色圆点则表示目标点的扩展邻域像素点,本文算法只选取最外侧的像素点。

结合式（4）和式（5），可以分别计算出扩展邻域序列 hn与 ln在时-频域上短时傅里叶变换时频幅值，分别记为Sft(i±2,j)与Sft(i,j±2)。结合式（6）-式（8），分别计算每组邻域信号的短时傅里叶变换时频幅值的均值af(i±2,j)，af(i,j±2)，标准差bf(i±2,j)，bf( i ,j±2)与标准差均值 Cn。本文通过设定阈值 T2与Cn作比较，并结合式（9）中的目标信号特征作进一步判别，判定关系如下

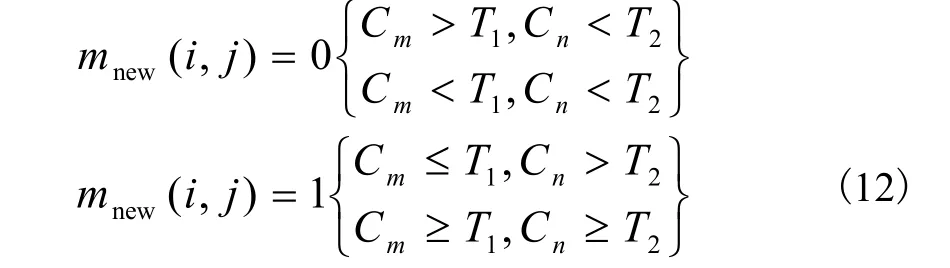
式（12）通过双阈值最终判断出目标点的信号特征。当目标点标准差均值大于阈值 T1，首先判定其为冲击信号，如果目标点邻域点的标准差均值小于阈值T2，则说明目标点周围是平稳信号，则该点为高频噪声将其去掉，其余点为运动目标点。当目标点标准差的均值小于阈值T1，首先判定其为平稳信号，如果目标点邻域点的标准差均值大于阈值 T2，则说明目标点周围是冲击信号，则该点为像素变化较小的运动目标将其保留，其余点为静态背景。

本文通过空域时域与频率的三域融合，提出 TSFF算法，可在连续多帧图像中，最大程度检测出运动目标，去除绝大部分背景噪声。

3 试验结果与分析

变电站视频拍摄地点为某县35 kV变电站，拍摄视频设备为 Microvision公司的 CCD工业相机，型号为MV-VS220，分辨率为 720×480像素。试验所用计算机为英特尔I5处理器，2g内存，Win7操作系统，所用程序均为Matlab2014编写。

首先对文中提到的帧间差分法（IFD）、鲁棒性主成分分析法（RPCA）算法中的快速完成主成分寻踪（FPCP）算法与自适应子空间跟踪（GRASTA）算法，以及自适应背景更新算法中的视觉背景提取（Vibe）算法与混合高斯模型（GMM）算法与本文提出的TSFF算法作了比较。试验分别选取了5组变电站不同工作环境下不同工作人员的视频帧作比较分析。由于在TSFF算法中，必须对连续多帧进行遍历计算，所以分别选取了5组变电站视频目标帧的前后相邻5帧，同时为了弥补在时频变换时信号长度较短的不足，文本将这相邻5帧信号重复排列4次，扩展为20帧长的信号。图2为变电站视频A处理效果比较，该视频背景扰动较小，目标运动速率适中；图3为变电站视频C处理效果比较，视频中存在多个运动目标，且目标运动速率较快。图4为变电站视频D处理效果比较，背景受到树叶的高频噪声扰动影响。且视频 A中的运动目标距相机较近，目标图像占比较大，背景相对简单；视频C和D中运动目标距相机较远，图像占比较小，背景相对复杂。

图2 不同算法变电站视频A处理效果Fig.2 Processed result of substation video A by different algorithm

图3 不同算法变电站视频C处理效果Fig.3 Processed result of substation video C by different algorithm

图4 不同算法变电站视频D处理效果Fig.4 Processed result of substation video D by different algorithm

同时为了与其他分割算法效果作横向比较，参数设定统一。其中帧间差分法（IFD）的二值化阈值设定为15；混合高斯模型（GMM）算法滤波器个数为3，初始背景建模帧数为10，学习速率为0.7；ViBe算法样本集中邻近像素点个数20，匹配点的个数阈值20，#min =2，更新采样概率为16。TSFF算法中短时傅里叶变换采用了窗长为3的海明窗，频率采样点数为128。试验结果详见图2、3、4。

接下来本文针对图2中变电站视频帧短时傅里叶变化部分特征信号的频谱图作了展示。详见图5。

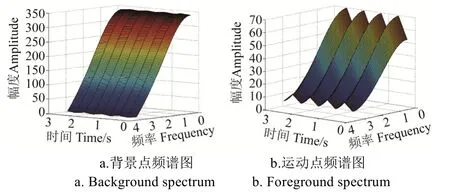
图5 不同特征信号频谱图Fig.5 Different characteristics of signal spectrum

图5a展示了5帧图像中坐标为（110,220）的静态背景点生成的频谱图；图5b展示了5帧图像中坐标为（217,398）的运动目标点生成的频谱图。通过2幅频谱图比较，可以明显看出：静态背景点即平稳信号生成的频谱图整体较为平缓，没有明显的波动；运动目标点即冲击信号生成的频谱图波动明显，出现多个波峰与波谷。根据这一信号特征，本文通过设定阈值1T，首先分割出连续多帧图像中的波动明显的运动信号。接着跟据式（10）～式（12）结合空域中目标点扩展邻域短时傅里叶变换对目标点信号特征作进一步判断，最终判别不同目标为静态背景、运动目标或者高频噪声。图7和图8分别展示了部分特征信号及其空间扩展邻域信号的频谱图。

图 6展示了图 2中变电站视频图像帧中坐标为（217,398）的目标点及其空间扩展邻域4点生成的频谱图；图 7展示了图 2中变电站视频图像帧中坐标为（118,558）的目标点及其空间扩展邻域4点生成的频谱图。通过2幅频谱图比较，可以明显看出在结合空域信息后，可以有助于进一步判断目标点信号特征：图 6a中目标点为冲击信号，图6b中其4个扩展邻域点（空域）也为冲击信号，所以该点判定为运动目标点。在图7a中，虽然目标点阈值大于1T判定为冲击信号，但在图7b中其4个扩展邻域点（空域）整体评价结果小于2T，所以该冲击信号目标点最终判定为高频背景噪声点剔除。采用本文双阈值判定算法同样可以识别出大量误识别为静态背景的运动目标点，减少生成目标图像的空洞现象。

由图8对比分析，双阈值算法保留了更多目标有效信息，且背景去噪效果更好。为了更精确地比较几种算法的性能，本文采用准确率和召回率作为量化指标，有公式

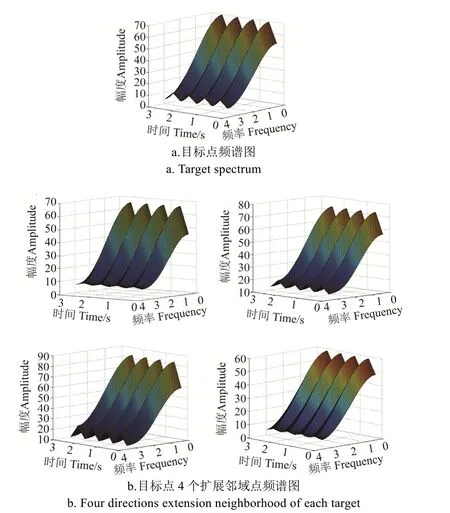
图6 运动目标点及其扩展邻域频谱图Fig.6 Moving target and extended neighborhood spectrum diagram

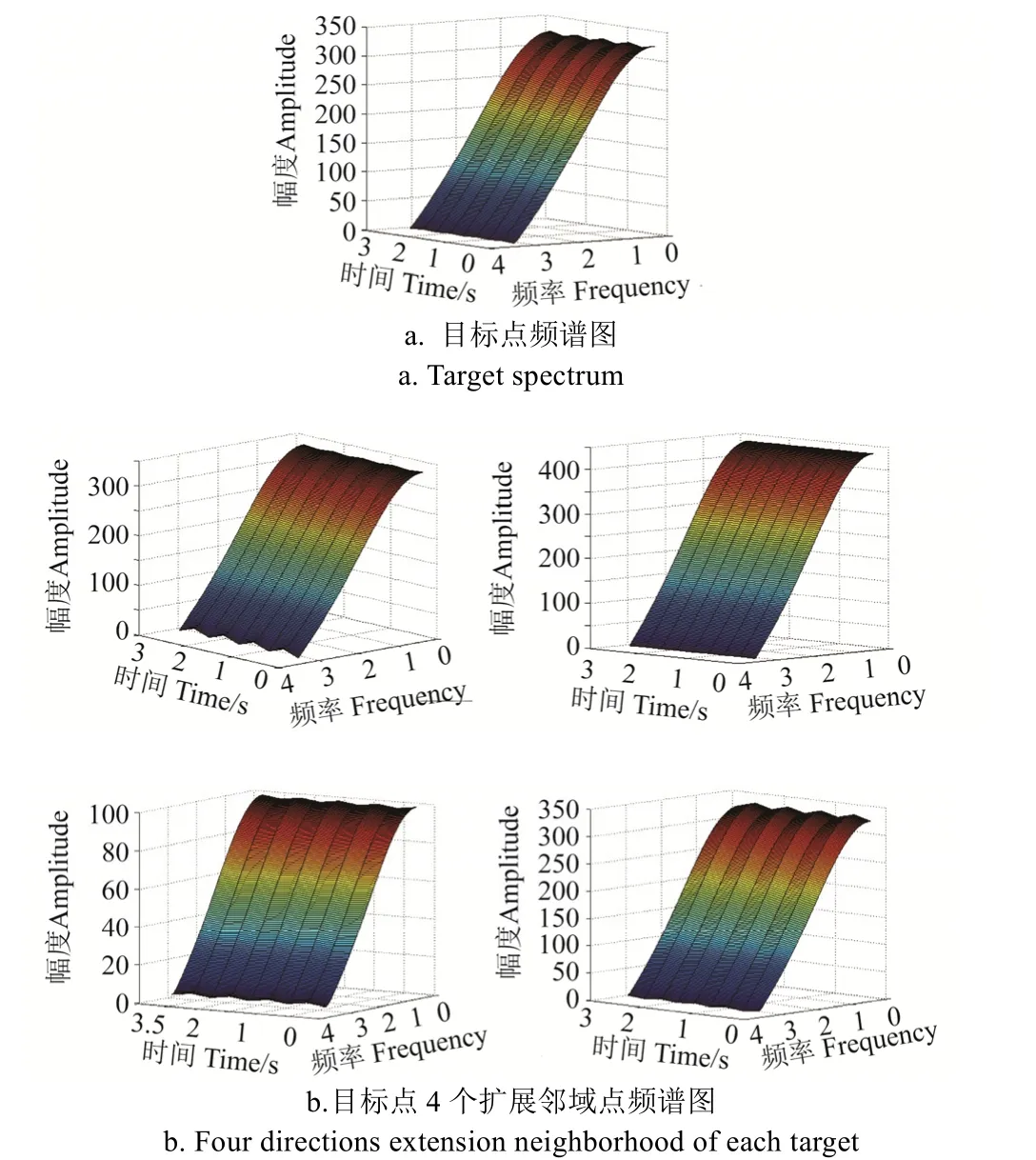
图7 背景噪声点及其扩展邻域频谱图Fig.7 Background noise and extended neighborhood spectrum diagram

式中P表示检测准确率；R表示检测召回率；Nj表示正确检测出的运动目标像素数；Nz表示算法实际检测出的运动目标像素数；NG表示真值图（ground truth）的运动目标像素数；准确率反映了正确检测的像素数占检测出的前景总像素数的百分比；召回率反映了正确检测的像素数占真值图像素数的百分比。表1列出了图2、3、4中不同算法检测效果的准确率与召回率。

本文提出的时空域与频域融合算法的运动目标信息保留效果在几种算法中表现最优，召回率为86.10%；背景噪效果（准确率96.68%）与IFD算法相当，整体表现优于其他算法。该算法在较完整保留运动目标信息的同时，最大限度去除了背景，且具有较强的鲁棒性，适用于在不同情况下变电站工作人员实时准确监测。

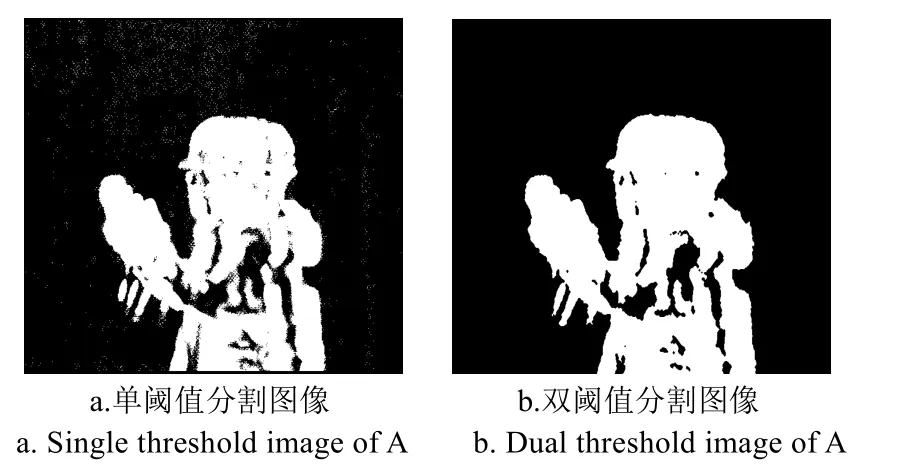
图8 单阈值与双阈值的视频A目标检测情况Fig. 8 Different video A moving target detection with different threshold

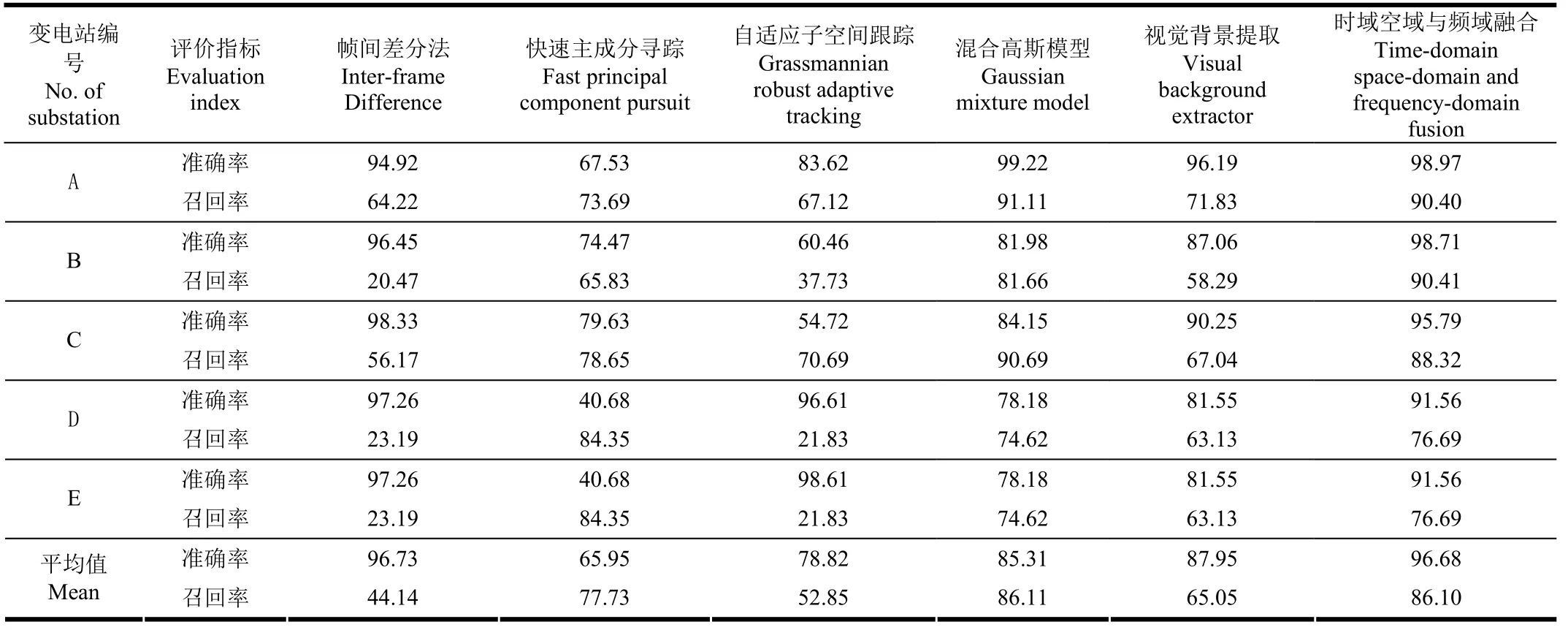
表1 不同算法检测效果的准确率与召回率Table 1 Performance of different algorithms through precision and recall rate %

4 结 论

1）本文结合中国农村变电站规模比较大，电气设备比较传统、设备自动化和智能化程度普遍较低特点，采取一种在变电站现场特定的安全（检修）区域周围即时架设相机的方法对工作人员实时监控，该方法成本较低，操作简单，且监控预警效果良好。现场工作人员检测越完整，噪声去除效果越好，那么对工作人员的检测与定位越准确，安全性大大提高。

2）结合某农村变电站现场 5组代表性视频帧处理效果与表1列出的评价标准，几种算法在不同情况下综合比较可以得出：帧间差分算法去噪效果良好，但目标保留效果较差；快速主成分寻踪算法对于高频噪声扰动抑制较差（视频 D树叶）；自适应子空间跟踪算法在目标运动较慢时检测效果严重下滑（视频B）；高斯混合模型算法目标保留效果最优，但是对于阴影与高频噪声同样去除效果一般；视觉背景提取算法对噪声抑制表现良好，但是目标保留效果整体一般。

3）本文提出的时空域与频域融合算法在处理不同情况下的视频帧表现稳定，通过双阈值的设定，比单阈值处理效果上均有较大程度的提升。且运动目标信息保留效果（召回率86.10%）在几种算法中表现最优；背景噪效果（准确率96.68%）与IFD算法相当，整体表现优于其他算法。该算法在较完整保留运动目标信息的同时，最大限度去除了背景，且具有较强的鲁棒性。适用于在不同情况下变电站工作人员实时准确监测。