改进双流体模型计算有液柱分离的管路水锤压力

富 友，蒋 劲 ，李燕辉，应 锐

（1.兰州理工大学能源与动力工程学院，兰州 730050；2.武汉大学水力机械过渡过程教育部重点实验室，武汉 430072）

0 引 言

当管路中的流动状态发生变化时，会产生水锤现象。水锤现象的发生、发展程度受管路材料特性和流动介质属性的影响[1]。就管路特性方面，材料的弹性模量对管路中的波速传递有着明显影响，特别对于薄管壁流动而言，水锤波的传递速度将会发生明显变化[2]，对于介质属性而言，密度、压力及热力学参数均对相应波的传递有明显的影响[3]。近些年在水锤计算研究方面，主要针对水锤波的传递过程中受管路几何结构的影响，管路水锤计算的流固耦合过程及水锤压力波的衰减过程方面进行了较为详细的研究[4-7]，但带有液柱分离现象的水锤计算一直为计算的难点，有较多的学者对该种现象进行过相应的研究分析，并取得了一定的成果[8-12]。当压力降低至饱和蒸气压力以下时，由于相变导致的液柱分离现象将会对压力响应的准确性造成更大的变化及影响[13]。

传统的水锤计算方法，通常采用连续性方程和动量方程进行构建计算模型，并采用特征线法进行求解计算。对于计算带有液柱分离的水锤现象时，通常采用离散空穴模型DVCM或DGCM模型进行计算，计算中当压力降低至饱和蒸气压时，将所计算的区域作为计算边界来计算相应的空穴率的变化[14-16]。

对于DVCM模型，Simpson 等[17]采用试验及数值计算进行验证，结果表明空穴率大于 10%时，压力峰值及持续时间均出现了明显的误差。

Bergant等[13]指出当空穴率大于10%时，由于交界面的问题，将导致泡状流动下的离散空泡的交界条件不再适用。Wylie曾将一小部分自由气体引入计算模型中，进而阻止数值震荡的出现[18]。也有学者对带有此类不可溶性气体的计算方法（DGCM 模型）进行研究，但自由气体体积的含量具有不可确定性[1]，同时体积的量级对于计算的压力变换有明显的影响[19]，该方法也受到一定质疑。不可溶性气体的存在，使得水锤现象可以从两相流的角度模拟计算[20-21]。在气液两相流动计算中，双流体模型是能够较为准确描述气液两相流动特征的计算方法，该方法认为各相的动力学特性不完全相同，模型由 1个空泡输运方程、2个连续性方程、2个动量方程及2个能量方程组成，在保证双相的可压缩性的前提下，方程具有良好的双曲性[22]，可为气液两相瞬变流动计算提供基础。

本文选用改进的双流体模型进行水锤计算模型的构建，并通过构建合理的相间作用形式及高精度的数值解法来描述带有液柱分离的气液两相流动现象。本文首先对于改进的双流体模型的数学特性进行分析，并选用全空化模型对相间质量变化进行计算，构建出一种考虑相间质量变化的气液两相瞬变流的计算方法。其次对方程中的不守恒项进行了单独处理并选用矢通量分裂(steger-warming flux vector splitting, SW-FVS)与无振荡，无自由参数，耗散算法 (non-oscillatory containing, no free parameters and dissipative scheme, NND)相结合的时间上为一阶，空间上均为二阶的数值方法进行数值计算。最后结合2个实验室的试验数据对2种弛豫方法对于计算结果的影响进行讨论分析。

1 改进的双流体计算模型

水锤计算模型是基于改进双流体模型建立，与传统的双流体模型的区别在于方程组中添加了管壁截面参数变量，这一改变也使得该计算模型更适用于管路中的气液两相流动计算。方程模型对液相和气相分别采用不同的压力、空穴率和密度进行描述。模型由 1个空泡输运方程，2个连续性方程，2个动量方程及2个能量方程组成。改进的模型方程的双曲型部分与文献[3，22-23]所示相似，其中一维的数值模型建立如式（1）～式（7）。

式中αk为空穴率；ρk为密度，ρ为混合密度，ρ1为相间密度，kg/m3，k=1代表气相，k=2代表液相；u为速度，m/s；λ为弛豫系数；Pk为压力，Pa；E为弹性模量，MPa；e为管壁厚度，m；m ˙g为质量传递率，kg/s；ck为介质波速，ckg为管内波速，m/s；D为直径，m；A为面积，m2；γk为比热比；τ为剪切应力，N/m2；Ek为总能量，J，Ek=ek+1/2uk2；ek为内能，J；θ 为管路倾斜角，(°)，γk为比热比。

1.1 闭合条件

由于计算中考虑了能量的变化，因此需要引入状态方程保证方程的封闭，这里采用修正的气体状态方程即SG-EOS[22]。

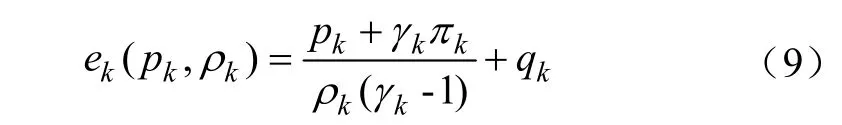
相间的内能变化如式（10）～式（12）所示。

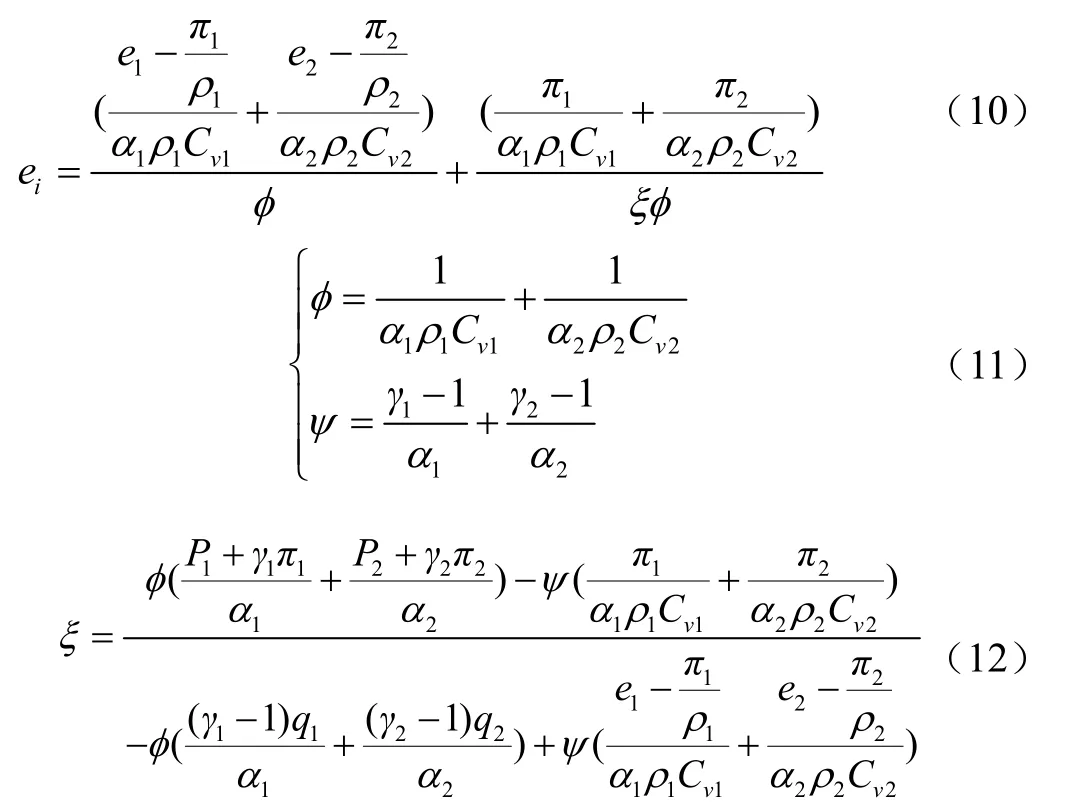
比热比γk，参考压力πk，焓qk，定压比热Cvk，定容比热Cpk参考文献[23-24]。在计算中π1认为大小为0（等同于理想气体状态方程），这一参数的取值带入波速方程后可得与声速方程一样表达式，γk与 π2采用式（13）、（14）进行计算。

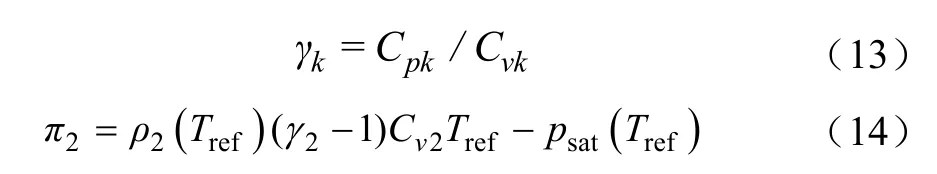
式中Tref为温度，K；psat为饱和蒸汽压力，Pa。

1.2 管壁变形的计算方法

计算中仅考虑一维流动，不考虑管道轴向的形变，仅考虑管壁径向上形变。同时管道内的压力变化仅仅对管壁内部横截面积造成影响，对于管壁厚度不造成影响。参照文献[19]，对管壁内的横截面积采用式（15）～（16）进行计算。

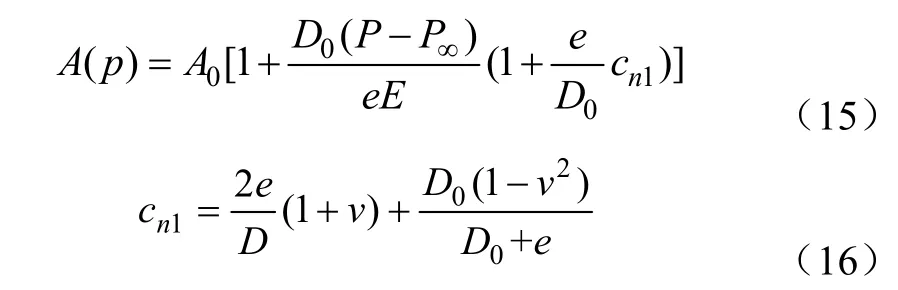
式中 A0为初始管壁面积，m2；P∞为初始压力，Pa，D0为初始管壁直径，m；cn1为管壁材质参数，v为泊松比。

2 数值计算方法

为得到更高求解精度下的计算结果，需要选用二阶或更高阶的求解格式进行数值求解计算，通常对于显示求解格式而言，高阶的求解格式往往会产生数值震荡，为了保证在处理压力震荡时的精确性及稳定性，本文选用NND格式进行求解计算。对于气液两相双流体模型而言，方程呈现非守恒形式，并包含不守恒项，因此采用高阶守恒格式的数值求解方法时，需要对相应的不守恒方程及不守恒项进行单独处理。

2.1 空穴输运方程的数值计算方法

方程(1)而言，由于无法将其写成守恒型格式，因此需要对空泡的输运方程进行单独处理，参照修正的Godunov scheme方法[22]，对方程（1）进行离散，其离散形式表现为式（17）～（18）。

2.2 双曲型算子计算方法

对于方程（1）～（7）而言，方程中守恒部分采用SW-FVS与NND相结合的方法进行计算。

NND是张涵信院士提出的一种数值计算方法[25]。其计算公式如式（21）～（24）所示。

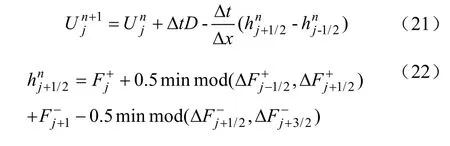
2.3 对于不守恒项的数值计算方法

将方程（2）～（3）、（4）～（5）依照式（21）写成相应的离散格式。

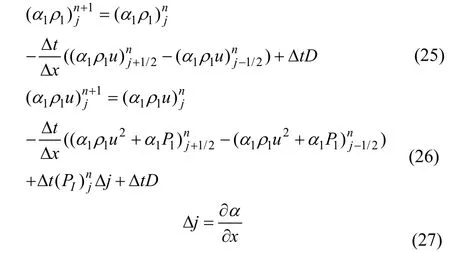
将方程（25）带入方程（26）中，根据文献[26]，可得表达式（28）与（29）。此时式（29）即为方程的不守恒项提供了相应的求解方法。

2.4 相间弛豫的计算方法

对于双流体模型下的气液两相瞬变流而言，气液两相分别具有各自的状态方程，并以此来描述各相的流动特性的变化。当产生瞬变波动时，从波速方程中可以看出，不同相间将会产生不同量级的波[27]。

随着压力波的传递，两相必将会产生相异的压力。对于流动而言，介质不可能长时间保持彼此相异的环境压力，需要一个平衡的状态来描述该过程，同时这个过程也将导致两相体积及内能的相应变化。通常对于两相压力的平衡过程是一个二维或三维的平衡过程。对于一维管道流动而言，采用更高维度的计算方法将使计算变的更加复杂，因此需要构建适用于一维求解的计算方法。

2.4.1 有限相间弛豫现象计算方法

由方程组（1）～（7）可知，方程右侧存在计算压力弛豫的源项，即λ（P1-P2）。对于采用两相瞬变流动的计算方法，可采用有限弛豫压力系数来进行构建[28-30]，其构建形式一般如式（30）形式。

式中AI为单体体积下泡粒表面积，N为泡粒数量。

这种方法需引入泡粒交界面的计算方程，同时需要考虑泡粒的脱落与融合。对于泡粒的直径，数量密度的假设将会大大限制计算的稳定性。并考虑到泡粒面积的改变，需要引入相间质量的描述方式。对于交界面质量变化的计算方法，一般认为流动中存在 3种物质，即空气、水蒸气和水。当压力降低至饱和蒸气压力以下时，控制体内将发生空化现象。选用全空化模型进行计算相间质量变化，全空化模型是由Singhal等[30]提出。模型考虑流动中的不可溶性气体，同时具有经验系数少，计算准确等特点。该种模型在CFD商业软件中有较为广泛的应用，其蒸腾和凝结过程采用式 （31）～（34）计算。

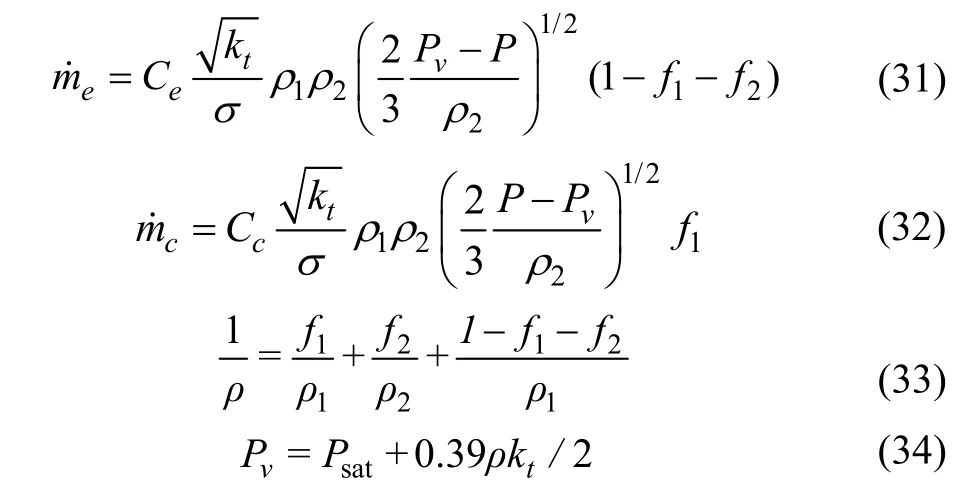
式中 kt为湍动能，m2/s2；fk为质量分数；Cc、Ce通常取0.01和0.02；σ为张力，N/m。

2.4.2 无限相间弛豫现象计算方法

当认为压力弛豫现象的计算过程远远小于时间步长时，可认为压力弛豫系数变换为无限大，此时可对每次计算后的结果进行修正，以此来达到对于弛豫现象的描述。在使用无限弛豫现象修正方法的过程中，不需要采用空化模型来描述相间的质量变化，该种方法已对相间的作用做出修正和描述。修正时源项对于空间的偏微分对计算不产生影响，参考相关文献[22]有式（35）～（39）。

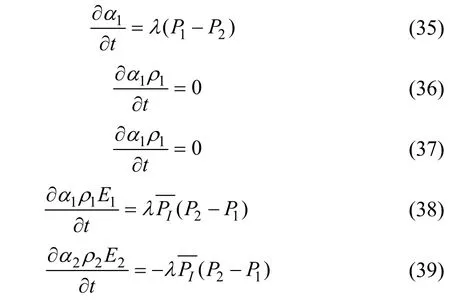
将式（35）带入式（38）、（39）中，可以得到式（40）。

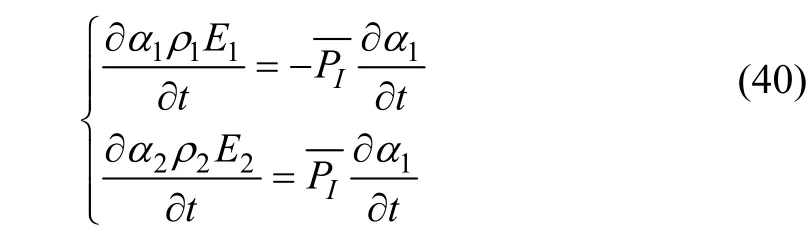
将式（40）进行积分可以得到式（41）。

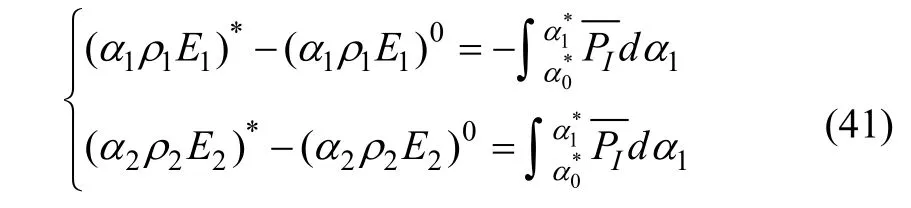
式中上标0表示双曲算子后的计算结果，上标*表示弛豫过程后的计算结果。将方程进行进一步整理可得式（42）。

将状态方程（9）、相间压力计算方程进行带入，同时由于π1通常取为0，因此有式（43）。

同时从式（38）、（39）可知，过大的泡粒直径将导致弛豫系数增大，进而导致弛豫系数对于相间能量的反向修正[31-32]，也验证了2.4.1中的结论。

2.5 边界条件

对于管道气液两相流动的上、下游的边界条件，采用特征线法进行构建，在构建时一般需要知道上游、下游的速度或压力的变化，以此来计算其他流动参数的变化趋势。其中相容性方程采用式（45）进行插值计算。

3 数值计算及试验比对

为验证该计算模型的适用性及准确性，选用了 2个实验室的不同试验数据，分别与数值模拟的结果进行对比，试验包括辛普森的关阀水锤试验[33]、武汉大学的水锤试验。

3.1 辛普森关阀水锤试验

辛普森关阀试验由四部分组成，分别为上游稳压水池、管线、尾阀和下游水池组成。图 1为辛普森关阀试验示意图。

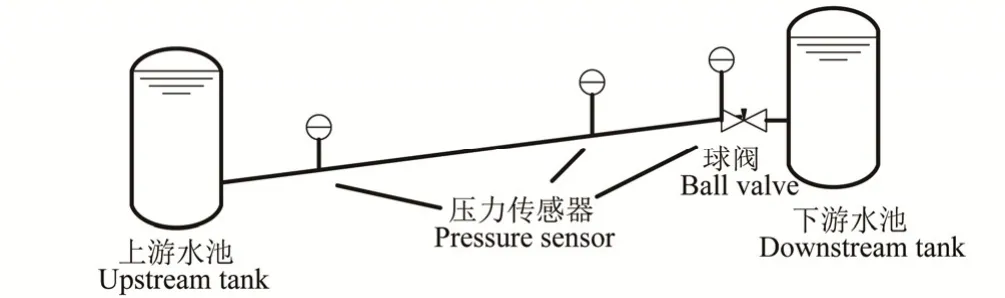
图1 辛普森试验示意图Fig. 1 Sketch of Simpson’s experiment

管线总长为36 m，直径为 0.019 05 m，厚度为 0.001 588 m，管道在9 m位置处有一90º转接头，管道末端连接低位水池，在管线36 m位置安装有一球阀。管线具有1 m高的坡度，在管线沿线有3处压力检测点，分别位于9、27、36 m。计算初始空穴率为10-7，上游稳压水箱压力为31.88 m，流速为1.125 m/s，管线阻力损失为2.8 m，饱和蒸气压力为3 032.17 Pa，波速为1 280 m/s，流体主要参数均参考文献[32]。水和空气的密度分别为998.2、2.52 kg/m3，饱和水蒸气的密度为0.077 14 kg/m3。表1为所对应的流体固有热力学参数。模拟计算以尾阀处速度边界进行读入，关阀时间为0.043 07 s。图2为辛普森关阀试验结果与计算结果比对图。

表1 辛普森试验热力学参数Table 1 EOS parameters for liquid and gas for Simpson’s experiment

图2 辛普森试验结果与计算结果比对Fig. 2 Comparison between model and experiments in Simpson’s experiment

由图 2可知，当采用有限弛豫系数计算方法时，如果不加入空化模型，那么计算结果与试验数据将出现极大的差异。从采用有限弛豫系数计算方法并引入空化模型的计算中可以看出，当泡粒数量（单位体积下泡粒数）选定为 1013时，计算结果与试验有较好的相似度，且泡粒数量选择量级与文献[34-35]描述一致。

在计算中发现，泡粒数量对于计算结果有明显的影响，当泡粒数量小于1013时，如图3中所示会出现次级波峰的响应时间出现偏差。当泡粒数量大于 1013时，会因为单位浓度下的泡粒表面积过大导致相间的动量传递超过真实计算值，造成内能和压力的反向修正，从而导致计算中断[31]。

图3 不同泡粒数量对辛普森试验的影响Fig. 3 Effect of different particle concentration in Simpson’s experiment

从图 2计算结果中可以看出，虽无限弛豫系数的计算结果较当泡粒数量选定为 1013时的计算结果有一定偏差，但与试验值的偏差同样较小。同时通过图2d空穴率的比对可以看出，2种计算方法计算的空穴率的变化虽然有一定偏差，但空穴率的变化趋势相似性较高。

图4 采用不同弛豫计算方法时气液两相压力差Fig. 4 Difference of gas-liquid two-phase pressure difference with different relaxation calculation methods

图 4为采用无限弛豫系数修正前气相压力与液相压力差，与采用有限弛豫系数并选用空化模型下的压力差对比图。由图 4可知，采用无限弛豫系数修正前，在压力低于饱和蒸气压力的空化初生区，气相压力始终大于液相压力。由式（42）可知，采用无限弛豫系数，正是对相间的能量变化进行修正，能量的变化虽然没有体现出相变，但从本质上来说，可以看成是伴随着能量变化的另一种相变表达形式，因此该种修正方法下不需要再次加入相变修正模型。同样从图4中可以看出当在0.3 s左右，正压力返回至末端时，对于采用有限弛豫系数修正的方法依然造成了压力相修正的偏差。当选用的泡粒数量继续增大时，将会出现反向修正的情况。

由于无限压力弛豫计算方法为一种强制性的修正计算方法，即在每个时间步长后，认为气相、液相压力均达到平衡状态，而事实上压力的弛豫时间通常为1 ms。若计算时间步长小于1 ms时，由于计算方法的强制修正，使得未到达平衡状态下的两相流动强制处于平衡状态，这也导致了空穴体积的修正偏大，使得在低压区的空化模型作用被大幅度消减。

3.2 管线上游水锤关阀试验

为模拟离心泵突然失电后关阀导致的管路系统中压力瞬变，本文在武汉大学水力机械过渡过程实验室，对此做了相应试验进行对比验证。试验管路系统布置如图5所示。试验由水箱、水泵、阀门、压力传感器、电磁流量计及水平管线组成，其中试验段管线总长为 97.6 m，管径为0.1 m，管壁材料为镀锌钢管，管壁厚为3 mm，折算管壁声速约为1 260 m/s；末端为高位恒压水箱，水位高度为 26 m。水和空气的密度分别为 998.2和 2.52 kg/m3，饱和水蒸气的密度为 0.077 14 kg/m3。试验中采取电动蝶阀进行快关试验。计算中选用无限弛豫计算方法进行计算。试验数据如表2所示。

图5 试验管路系统布置图Fig. 5 Layout drawing of test piping system

表2 试验初始数据Table 2 Initial conditions of experiment

对于压力的测试，采用阀门位置（压力传感器P1点所在位置）和0.5倍管线位置（压力传感器P2点所在位置）进行数据采集。试验采用武汉超宇测控技术有限公司生产的 CY 3088型号压力变送器，测量范围为 0～5.0 MPa（绝对压力），测量精度为 0.5%，流量计为KROHNE生产的IFM 4080K电磁流量计，测量范围为0～80 m3/h，测量精度为0.5%，试验系统中的仪表精度等级直接决定了试验台的测试精度，在本章试验系统中试验台总测试系统的系统误差为±0.933 8%。试验中选用的测量仪器输出均为电流信号，采用数据采集卡将电流设备转换为数值信号，并通过传输存储于计算机指定位置上。表 3为关阀试验热力学参数。将计算结果和试验结果进行比对，如图6所示。由图6可知，计算结果与试验结果吻合程度较高，验证了算法的可行性。

表4为试验对比误差。由表4可知，试验1和试验2压力波峰值均超过Joukowsky水锤定律（a△u/g）计算值，证明瞬变流动中产生了明显的液柱分离现象，同时通过压力峰值与试验值的计算偏差可以看出计算值与试验值偏差较小，验证了数值方法的准确性。

表3 关阀试验热力学参数Table 3 EOS parameters for liquid and vapor water for experiment

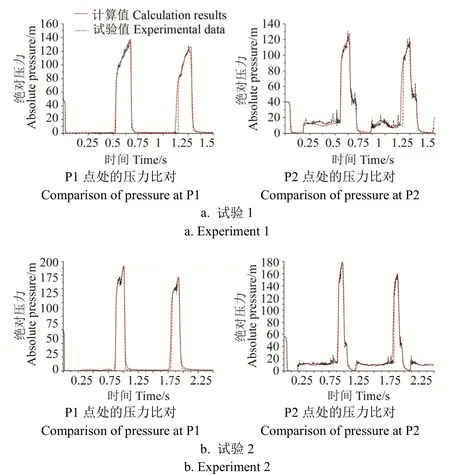
图6 关阀试验结果与计算结果对比Fig. 6 Comparison between experimental data and calculation data in water hammer experiment

表4 试验对比误差Table 4 Error comparison between experimental and calculation

综上 2个实验室的不同试验可以看出无限弛豫系数无空化模型的计算方法可以较好的模拟管路系统中，由于关阀所造成的水力过渡的压力瞬变，并可以较为精准的预测管路系统的过渡过程。同时相对于以往的气液两相计算模型[37]而言，本文所选用的计算模型，去掉了泡状流假设，可以使得计算的稳定性得到更好的保障。

4 结 论

本文基于改进的双流体气液两相流计算模型，对管道中由于水锤造成的液柱分离的气液两相瞬变流动进行计算分析比对，计算中考虑了管壁截面随压力变化时对波速的影响，并对方程中的不守恒项及不守恒方程进行了单独处理，以确保模型计算的稳定性。通过对比两种弛豫计算方法对于计算的影响，并采用辛普森关阀试验与管线上游水锤关阀试验进行分析比对论证，结论如下：

1）采用有限弛豫参数计算时，需考虑由于空化引起的相变，同时需选择合理的泡粒数量以保证计算精确度。

2）采用无限弛豫参数计算时，空化模型对于计算结果影响较小，可直接对水锤现象造成的液柱分离现象进行分析模拟，但会造成空穴率计算结果过大。

3）采用改进的双流体气液两相流计算模型，并构建合理的数值计算方法及弛豫系数，可以对带有明显液柱分离现象的管路气液两相瞬变现象进行预测计算，该方法计算精度高，对于工业管道中的水锤防护计算具有较好的应用价值。