正项级数学习中常见的几个问题

摘 要：正项级数在级数中是重要的理论基础，本文主要针对学习正项级数时会出现的一些常见问题进行了归纳总结。

關键词：正项级数；收敛；问题

级数是高等数学的重要章节，它不但能够描述许多自然现象和工程技术中的客观规律，而且可以近似计算无理数。正项级数作为级数重要的基础理论，在解决很多级数问题中起着非常重要的作用。这节的内容比较多，关系复杂，很多初学者在学习过程中，存在很多疑惑，现将其归纳几个问题如下：

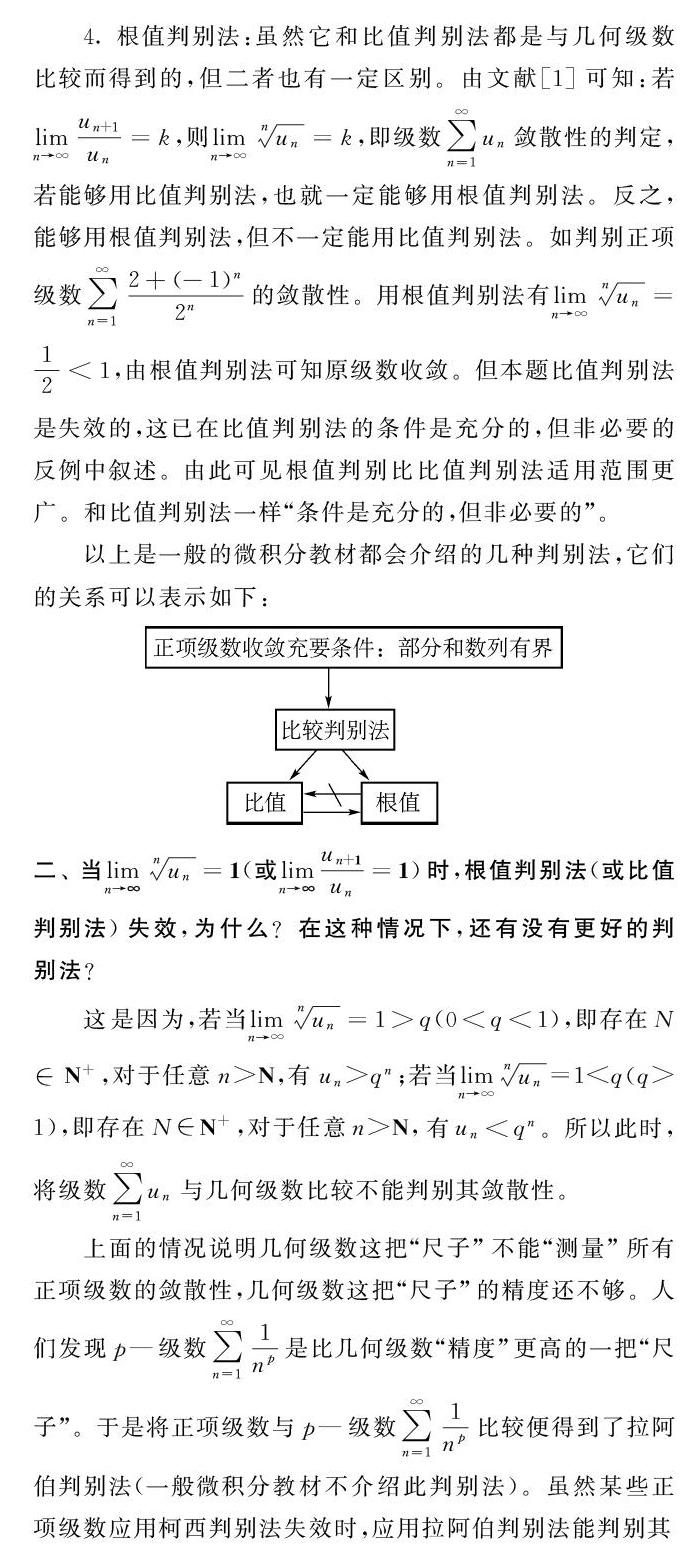
一、 判别正项级数敛散性的方法一般有哪些？它们有哪些优缺点？它们之间有何关系？

1 正项级数收敛的充要条件是它的部分和数列有上界。这是正项级数敛散性判别法的理论基础，它的结论虽然完美，但应用起来往往困难。因此在它的基础上人们研究出了一些更具体、更有针对性的判别法。

2 比较判别法：它有不等式形式与极限形式两种表达形式，其中极限形式在解题中用起来比较方便。比较原则的基本思想就是通过与某一个正项级数（敛散性已知）的比较来确定另外一个正项级数的敛散性。这也是比较判别法的一个缺点，即须有参考级数的敛散性。常用的参考级数：（1）几何级数，（2）P-级数，（3）调和级数。

三、 判别正项级数的敛散性一般程序是什么？

正项级数敛散性的判别程序一般如下图：

有时候一个级数敛散性的判定是一个复杂的过程，单纯地使用一种判别法往往是不够的，需要级数的性质和几种判别法并用方可解决问题。

参考文献：

[1] 刘玉莲，傅沛仁.数学分析讲义[M].北京：高等教育出版社，1996.

[2] 关汝华，孟凡洪，刘家春.微积分[M].长春：东北师范大学出版社，2012.

[3] 同济大学数学教研室.高等数学[M].北京：高等教育出版社，2004.

作者简介：卢兰，吉林省长春市，长春光华学院基础教研部。