加权全局上下文感知相关滤波视觉跟踪算法
2018-08-20张春辉
万 欣,张春辉,张 琳,周 凡
WAN Xin1,ZHANG Chunhui2,3,ZHANG Lin1,ZHOU Fan1
1.上海海事大学 信息工程学院,上海 201306
2.中国科学院大学 网络空间安全学院,北京 100049
3.中国科学院信息工程研究所 信息安全国家重点实验室,北京 100093
1.College of Information Engineering,Shanghai Maritime University,Shanghai 201306,China
2.School of Cyber Security,University of ChineseAcademy of Sciences,Beijing 100049,China
3.State Key Laboratory of Information Security,Institute of Information Engineering,Chinese Academy of Sciences,Beijing 100093,China
1 引言
视觉跟踪是计算机视觉研究领域的一个前沿方向,其在智能监控、机器人视觉、人机交互、虚拟现实等众多富有挑战性的场景中都起到了关键性的作用。自从Bolme等人[1]提出MOSSE算法以来,相关滤波器(Correlation Filter,CF)已被广泛认可为解决视觉跟踪问题的一种稳健且有效的方法。目前基于CF的跟踪器在OTB-50[2]、OTB-100[3]、UAV123[4]、TC-128[5]、ALOV300++[6]、VOT2015[7]等当前主流基准测试中排名都非常靠前,同时保持较高的计算效率。
现在对CF跟踪器的改进主要包括纳入kernels[8]和HOG[9]特征,添加color name特征或color直方图[10],集成稀疏跟踪器[11],采用自适应尺度[12],缓解边界效应[13]以及与深度CNN特征[14]整合。目前的研究重点是解决CF跟踪器固有的缺陷,即扩大其适用范围。Liu等人[15]提出基于部分的跟踪技术以降低对部分遮挡的敏感度,并更好地保留对象结构。Ma等人[16]提出通过关联时间上下文和训练在线随机蕨丛分类器进行重新检测,实现对外观变化场景长期的稳健跟踪。Zhu等人[17]提出了一种协同CF跟踪器,它结合了一个多尺度的核化CF来处理在线CUR滤波器的尺度变化,以解决目标漂移的问题。该方法通过结合外部分类器来辅助CF或利用其高计算速度来同时运行多个CF跟踪器以提高性能。Sui等人[18]提出了一种新的峰值强度指标来度量学习到的相关滤波器的判别能力,可以有效地增强相关响应的峰值,使得滤波器具有更强的辨别能力。Dinh等人[19]在相关研究中尝试了使用上下文进行跟踪,使用顺序随机森林、非线性模板外观模型和局部特征来检测无关上下文和跟踪目标。此外,Xiao等人[20]在最近的工作中,通过场景上下文信息的多层次聚类检测相似物体和干扰物体,然后经过在线学习获得全局动态约束,实现无关区域与感兴趣目标的区分。然而,这些跟踪器普遍存在的缺陷是没有很好的泛化能力。
最近的研究发现,通过修改用于训练的常规CF模型,可以直接克服其中一些固有的局限性。例如,通过将CF跟踪器中的岭回归作为目标响应的一部分,Bibi等人[21]的工作显著降低了跟踪目标漂移带来的影响,同时保持较高的计算效率。Mueller等人[22]提出了(Context-Aware,CA)框架,该框架可以与许多经典的CF跟踪器进行集成。但是CA框架所存在的最大缺陷是未对上下文环境信息进行细化处理,即CA框架同等地对待目标对象邻域内的整个上下文区域,认为整个上下文区域对跟踪的贡献相同,削弱了全局上下文在目标检测中的重要作用。在现实情景中,上下文环境普遍包含十分复杂的信息,有目的性地对不同的区域进行细化,将有利于提高算法的健壮性。为了充分发挥全局上下文的作用,本文运用动态分区的思想,根据上下文中不同区域与追踪目标运动相似度大小,对不同区域赋予不同的权值,提出基于加权全局上下文感知(Weighted Global Context-Aware,WGCA)框架的相关滤波视觉跟踪算法。通过利用加权全局上下文信息,WGCA框架与经典的跟踪器SAMF[23]相结合的SAMFWGCA算法,可以获得比大多数主流的跟踪器更好的跟踪结果(见图1)。可以发现,它的跟踪效果甚至优于新近提出的HCFT[24]跟踪器,实际上HCFT算法的分层卷积特征中已经隐含了上下文环境的信息。

图1 SAMFWGCA与其他跟踪器效果截图
本文的主要创新和贡献点如下:
(1)提出了基于加权全局上下文感知的视觉跟踪框架,可以被广泛地应用于目前主流的CF视觉跟踪器。
(2)通过求闭式解可以使集成的CF跟踪器保持较高的运算效率,同时显著提高它们的性能。
(3)在主流数据集上的测试结果表明提出的加权全局上下文感知框架是有效的。同时,也对所提出的WGCA框架做了鲁棒性方面的评估,进一步验证了该框架出色的性能。
2 传统CF跟踪器
传统CF跟踪器[25]的核心是使用判别学习。目标是学习连续帧中的感兴趣区域以推断目标的位置,即滤波器响应最大的位置[26],并得到判别相关滤波器w。CF跟踪器被广泛使用和成功的关键因素是其采用的抽样方法[27]。基于相关滤波的CF跟踪器本质上是采用密集采样策略,由于计算能力的限制,通常的做法是在目标周围随机挑选有限数量的负样本。采样策略的复杂性和负样本的数量可能会对跟踪性能产生重大影响。CF跟踪器可以在目标周围进行密集采样,并且只需付出较低的计算成本,这是通过将目标在搜索窗口内的所有可能的变换建模为循环移位,并将它们连接以形成数据矩阵A0来实现的。该矩阵的循环结构有助于求解傅里叶域中的以下岭回归问题:

式中,矢量w表示相关滤波器;方阵A0包含矢量化图像块a0的所有循环移位。记上述回归目标为y,其为二维高斯矢量化图像。
如果X是循环矩阵,对其进行下面的变换将可以快速求解方程(1):

其中,向量X的共轭为X∗;用表示X的傅里叶变换FHX,F是DFT矩阵。
2.1 原始域中的解
由于式(1)的目标函数为凸函数,且具有唯一的全局最小值,通过使其梯度值等于0可以得到滤波器的闭式解:又因为A0是循环矩阵,所以可以在傅里叶域中按照式(2)进行对角化和矩阵求逆有效地求出原始域中的解为:

最大响应的位置是搜索窗口内的目标所在位置,因此原始域中的检测公式由下式给出:
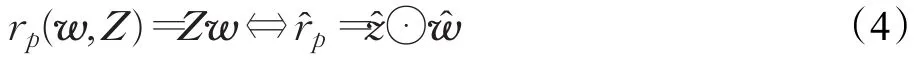
其中,滤波器w为搜索窗口,即图像块z的卷积;Z为图像块的循环矩阵。
2.2 对偶域中的解
式(1)也可以使用对偶域变量α在对偶域中求解。通过变换,对偶域中的闭式解可表示为α=类似于原始域,它可以在傅里叶域中被有效地求解,对偶域内的解为:

该解可以通过双积函数来表示,并且可以在对偶域中使用核技巧进行计算。通过把对偶域变量α表示为原始变量,可以直接用于目标检测。由此,可以得到以下对偶域中的检测公式:

3 基于上下文的CF跟踪器
3.1 全局上下文
根据运动相似度把全局上下文分为4类,包括目标区域、支撑区域、无关区域及干扰区域[28]。目标区域是跟踪对象所在的区域;支撑区域是与跟踪对象的运动方向基本一致或相同的那些区域;无关区域是指始终静止不动的背景区域;干扰区域是指与跟踪对象的运动方向偏差很大甚至截然相反,以及出现遮挡的那些区域。
图2给出了一个完整的全局上下文区域划分的示意图。其中图像的颜色深度值代表所在区域与其他区域相似度的大小,深度值相同的区域为同一区域,并且两个区域的颜色深度值相差越大,说明它们的运动方向差异越大。中间高亮的区域代表跟踪目标。图中的字母表示根据不同区域运动相似度划分得到的分区结果。从图中可以得出E区域为目标区域,A和C区域为支撑区域,B、F及G区域是无关区域,D和H区域为干扰区域。仔细观察各个区域边界可以发现,这4类区域的形状并不是固定的,相互之间也没有显著的空间界限。同时,由于上下文区域的动态性,各区域的划分在跟踪过程中是随时间动态变化的,即存在所谓的时间上下文[29]的概念。在视频中相连的帧序列,跟踪目标自身所在区域也可能划分到不同区域中,例如当目标快速移动时,上一帧的目标区域会变成支撑区域,曾经的无关区域也可能变为支撑区域,特定情况下甚至转变成目标区域;当视频的某一帧发生遮挡时,原来的目标区域中的被遮挡部分就变成了干扰区域。

图2 全局上下文区域划分图
3.2 上下文感知CA框架
跟踪对象的周围环境可能会对跟踪性能产生很大影响[30]。例如,如果背景混乱,那么背景对于跟踪成功与否将产生十分重要的影响。Mueller等人[22]在最新的工作中提出了在学习阶段向过滤器添加上下文信息的CF跟踪框架CA。
基于CA框架的跟踪器在每一帧中,根据hard negative mining[31]采样策略对感兴趣的对象a0∈ℝn和其周围的k个上下文片段ai∈ℝn进行采样。它们所对应的循环矩阵分别为A0∈ℝn×n和Ai∈ℝn×n。这些上下文区域可被视为hard negative样本。它们包含各种干扰因素和不同形式的全局背景。本文要解决的问题是求一个相关滤波器w∈ℝn,该滤波器对目标区域有较高的反馈,对上下文区域反馈极低。通过将上下文区域作为正则项添加到式(1)中的岭回归问题获得新的回归目标。最终,将标准公式(式(1))中的目标区域回归为y(式(7)),而无关上下文区域则由参数λ2控制回归为0。
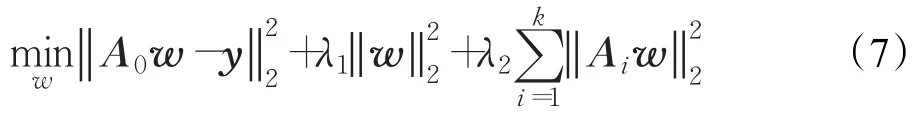
3.3 加权全局上下文感知WGCA框架
在CA框架中,要学习的全局上下文模型为式(7)中给出的数据矩阵A0。本文针对CA框架对上下文信息利用不充分的问题,综合考虑目标周围上下文环境中不同区域对跟踪目标的贡献权值,提出WGCA框架。因此,上述数据矩阵被重新定义为:

其中,B为加权全局上下文感知模型的数据矩阵;W为上下文对应的权值矩阵,下文将会详细介绍权值矩阵的计算方法。
本文提出的基于WGCA框架的视觉跟踪算法的整体运算步骤如下:
步骤1初始化全部所需的参数。
步骤2计算填充后的目标边界框的大小;用高斯函数表示与边界框大小成正比的回归目标;用汉宁窗法计算余弦窗值;创建视频界面。
步骤3从第1帧图像到第T帧图像,执行改进的相关滤波算法。
步骤3.1获取第1帧图像的目标边界框,在新的目标估计位置进行训练。选取目标区域周围的k个上下文环境,计算相应的权值矩阵(具体见3.3.3小节)。计算出第1帧图像在傅里叶域内的闭式解,作为滤波器模型的初始化。
步骤3.2从第2帧图像开始,从上一帧目标的位置获得目标边界框,并变换到傅里叶域。把相关滤波器反馈最大的区域作为目标的估计位置。获取目标边界框,在新的目标估计位置进行训练。选取目标区域周围的k个上下文环境,计算相应的权值矩阵(具体见3.3.3小节)。计算在傅里叶域内的闭式解。采用线性插值的方法更新滤波跟踪器。
步骤3.3保存上述两个步骤的目标边界框的位置坐标和运算时长;同时可视化滤波跟踪视频界面。
步骤4输出滤波跟踪器的中心位置误差、帧率、边界框重叠率;绘制成功率图、精度图等。
3.3.1 上下文权值矩阵
根据上下文环境中不同区域的物体的运动方向与目标中心的运动方向之间的相似度,来决定哪些区域对跟踪目标的定位起到更加关键的作用。那些与目标运动相似度比较高的支撑区域的作用通常比较大,应该赋予相对较高的权重,而那些无关区域和干扰区域,几乎不提供有用的跟踪信息,则赋予相对较小的权值,最终形成一个与上下文环境作用大小一致的权值矩阵。为了获取上下文环境中所有像素的运动信息,根据光流跟踪算法的结果来推算视频上一帧和下一帧对应点的位移,进而计算出运动轨迹。按Lucas-Kanade[32]稀疏光流算法获得离散点的权重,最后通过插值获得整个上下文环境的权值矩阵。
3.3.2 跟踪特征点的选择
特征点的选择对光流跟踪来说是十分重要的。根据对相关文献的分析,通常被选用的特征点有Harris角点[33]、Goodfeaturestotrack特征点[34]、SIFT特征点[35]、SURF特征点[36]和随机像素特征点[37]等。根据对上述特征点的总体性能进行分析,发现Harris角点在处理时间上具有明显的优势,并且可以获得足够数量的特征点,它的跟踪性能十分优异,跟踪稳定性也能被确保。因此,进行Lucas-Kanade稀疏光流跟踪时使用Harris角点作为特征点。
3.3.3 权值矩阵计算步骤
利用光流跟踪获得第t帧图像全局上下文环境的权值矩阵Wt的计算步骤如下:
输入:视频的第t-1帧和第t帧,尺度参数γ。
输出:全局上下文权值矩阵Wt。
步骤1读入视频序列,在第t-1帧提取一定数量的Harris角点,即
步骤2根据Lucas-Kanade算法,得出第t帧中对应的目标跟踪结果,即
步骤2.1删除跟踪产生的跟踪错误点。
步骤3计算第t帧跟踪目标中心位置与全部Harris角点之间运动的相似度。
步骤3.1计算得到该帧跟踪目标中心位置和所有Harris角点的位移向量
步骤3.2把上面的位移向量改写为极坐标,即是位移向量的极坐标形式,和代表位移向量的长度和角度。dx和dy为位移向量在x轴、y轴方向的分量。arctan为反正切函数,θ∈(-π,+π)。
步骤4计算目标中心位置与Harris角点之间的距离。该距离定义为目标中心位移向量与Harris角点位移向量之间的差,即:
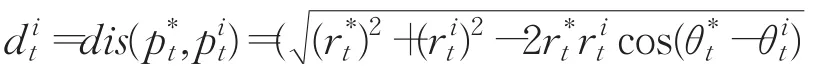
3.3.4 相关滤波器特性分析
从3.3.3小节权值矩阵计算步骤可知,本文提出的基于WGCA框架的相关滤波器有以下特性:因为支撑区域、目标区域内的像素与跟踪目标中心坐标的距离相对较小,所以支撑区域和目标区域内的像素能够得到相对较高的权重(见图3),即滤波器对支撑区域、目标区域将有较高的反馈。反之,处于干扰区域、无关区域内的像素,其最终的权重就小得多,即滤波器对干扰区域和无关上下文区域的响应较小。图3(b)是WGCA跟踪算法执行过程中在图3(a)所在帧中计算得到的上下文权值矩阵。灰度越浅表示权值越高,相应地滤波器对此区域的反馈越大。可见那些与目标运动相似度高的支撑区域、目标区域都有较高的权值,即得到了较大的反馈。

图3 加权全局上下文环境及对应的权值矩阵
3.4 单通道特征
3.4.1 原始域中的解
式(7)中的原始目标函数fp可以通过在目标区域上叠加加权全局上下文信息,得到新的数据矩阵B∈ℝ(k+1)n×n,新的回归目标∈ℝ(k+1)n。

其中:

由于fp(w,B)是凸函数,可以通过令其梯度为0来使其最小化,从而得到:

类似于式(1)中的CF跟踪器,按照式(2)在傅里叶域中做变换得到以下闭式解[38]:

它与式(4)所定义的标准公式本质上是一致的。
3.4.2 对偶域中的解
可以看出式(9)表示的原始域中的解与标准岭回归问题的解的形式完全相同。因此,CF跟踪器在对偶域中的解可由下式给出:
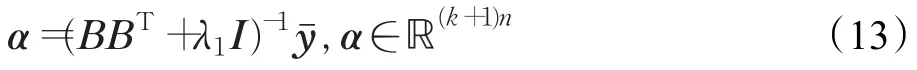
使用循环矩阵的恒等式得到:
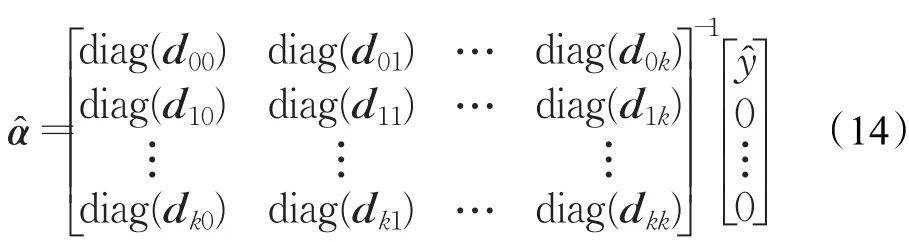
其中,向量djl,j,l∈{1,2,…,k},由下式给出:
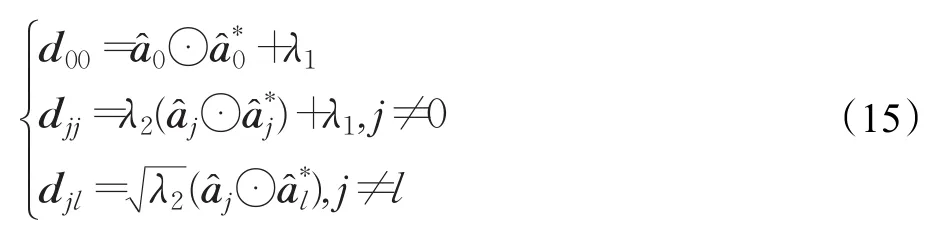
上式可以使用核技巧,因为图像块之间的所有相互作用都是同时发生的。从而线性相关性可以简单地由传统核化CF跟踪器的核相关性来代替。
所有的图像块矩阵都是对角的,因此系统分解为尺寸为ℝ(k+1)×(k+1)的n个小系统。这显著降低了复杂性,且可以实现并行计算。不再是通过求解ℝ(k+1)n×(k+1)n维的高维系统来计算α̂,而是对α的每个像素p∈{1,2,…,n}求解一个单独的系统,结果如下式所示:

由此式(6)中对偶域的检测公式可以根据上面的公式改写为rd(α,B,Z)=ZBTα。它与标准公式相似,但除了目标之外,B还包含加权全局上下文信息。又因为α∈ℝ(k+1)n由对偶变量{a0,a1,…,ak}组合而成,按照式(2)进行对角化变换,傅里叶域中的检测公式可以重写为:

3.5 多通道特征
3.5.1 原始域中的解
因为多通道特征通常可以比单通道特征(例如灰度强度)提供更丰富的目标表示,所以将式(7)推广到多通道特征并学习所有特征维度m的联合滤波器是很重要的。可以采用与单通道特征(式(12))类似的方式重写多通道原始目标函数但有以下不同:现在包括作为行的目标和上下文区域以及作为列的相应特征。用不同特征尺度的滤波器被堆叠成∈ℝnm。

最小化式(18)与单通道情况类似可得:使用循环矩阵的恒等式得到:


对于每个特征维度i,l∈{1,2,…,m}的跟踪目标和上下文图像区域分别用a0j和aij表示。那么块被定义为:
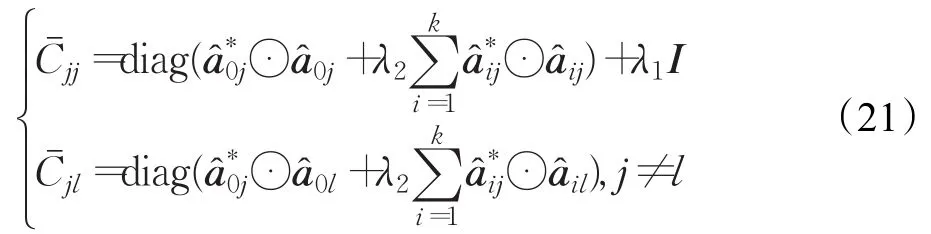
但是这个系统不像单通道情形(式(15))那样能够有效地求逆。然而所有块都可以表示为对角矩阵,因此系统可以分解成n个尺度为ℝm×m的较小系统,通过并行计算可以显著降低计算复杂度。类似于式(15),对于滤波器的每个像素p∈{1,2,…,n}可求解一个单独的系统。
多通道特征原始域内的检测公式与式(4)中的标准公式几乎相同,区别在于图像块z和学习的滤波器w是m维的。
3.5.2 对偶域中的解
与单通道特征的情况类似,多通道原始域中的解(式(19))与标准岭回归问题的解具有完全相同的形式,在对偶域中可以得到以下解:

再次,由循环矩阵(方程(2))的恒等式可得:

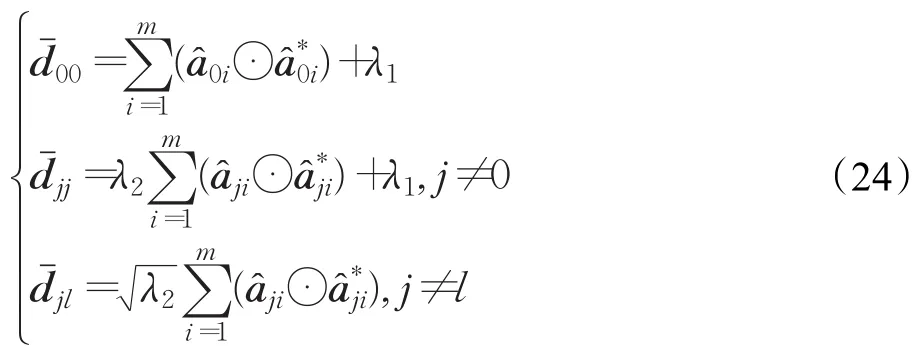
可以发现,上述线性系统与单通道特征的对偶域内的解(第3.4.2小节)的情况相似,只是现在要沿特征维度m进行一次求和。该解还能够使用核技巧、线性系统按照与单通道情况(式(16))相同的方式进行求解。
多通道特征对偶域内的检测公式和单通道特征对偶域内的情况类似,其差别在于和ℝ(k+1)n×nm现在具有多个特征维度列:对角化后进行重新改写,傅里叶域中的检测公式最终简化为:

3.6 对CF跟踪器的适用性分析
本文推导了滤波器在单通道特征、多通道特征和原始域、对偶域所有可能情形的闭式求解方法。在原始域单通道特征的情况下,该解仅包含基于元素的操作,并且实现是低代价的。在对偶域单通道特征情况下,需要对n个尺度为(k+1)×(k+1)的小系统进行求逆。它们中的每一个都可以改写为外积的形式,并且可以使用Sherman-Morrison[39]公式进行反演运算,从而可以非常有效地求解。
由于多通道情形的解包含原始域和对偶域的总和,不能将其改写为外积的形式。如果要求解的系统较小,则可以精确地求解。求解的复杂性取决于在原始域情况下选择的特征维数m或在对偶域情况下上下文区域的数量k。总体来说,求解n个小系统的复杂性较低,并且是系统密集的。如果m或k足够小,那么直接求解这些系统会非常高效。如果求解的系统较大(原始域为nm×nm维,对偶域为(k+1)n×(k+1)n维),它们通常十分稀疏。当m或k非常大时,则可以使用共轭梯度下降(CGD)[40]方法。对于原始域多通道特征,假设这m个特征是独立的,当使用HOG特征时,可以使用式(14)独立高效地计算每个特征维度的滤波器。对于对偶域多通道特征情形,目标区域和k个上下文区域通常也是相互独立的,则问题可以转化为类似于式(1)中多通道特征的正则岭回归问题,进而有效地求解。
通过以上分析可知,本文提出的WGCA框架CF跟踪算法可以采用求闭式解的方法,并且给出了各种特征在原始域和对偶域进行组合的解。因此在实际应用需求中,可以广泛应用于不同类型的主流CF视觉跟踪器,从而提高它们的目标跟踪性能。
4 实验结果及分析
首先,将WGCA框架与4种经典的CF跟踪器进行集成;然后,将它们与对应的基准版本跟踪器、目标自适应跟踪器以及CA跟踪器进行比较。此外还加入了一种加权时空上下文算法(Weighted Spatio-Temporal Context,WSTC)[28]进行对比分析。为了进行评估,在目前主流的跟踪数据集OTB-100上进行测试。
4.1 基准跟踪器
为了验证本文提出的WGCA框架的性能,选择了4种经典的CF跟踪器作为基准,表1总结了这几种CF跟踪器。本文将提出的WGCA框架应用于上述4个基准跟踪器,将它们称为MOSSEWGCA、DCFWGCA、SAMFWGCA和STAPLEWGCA。此外,将它们的目标自适应跟踪器称为MOSSEAT[41]、DCFAT[42]和SAMFAT[43]。把对应的基于CA框架的目标跟踪算法称为 MOSSECA、DCFCA、SAMFCA和STAPLECA。

表1 基准CF跟踪器
4.2 实验设置
4.2.1 评估指标
按照OTB-100中所定义的,首先使用以下两种测评方法对跟踪器进行性能评估:精度(Precision)和成功率(Success Rate)。
中心位置误差(Center Location Error,CLE)[2]是一种普遍使用的跟踪精度评估指标,指的是跟踪对象中心位置和基准的平均欧氏距离。在一些文献中提出采用精度图(Precision Plot)[4,44]来衡量跟踪算法的总体性能。精度图曲线表示给定阈值后,估计坐标和基准坐标的欧氏距离在阈值内的视频帧数的比例。通常阈值取20像素时,定义跟踪器的精度[45]。
边界框重叠率(Bounding Box Overlap)[2]是一种成功率度量的指标。若记跟踪器的边界框为rt,基准边界框为ra,那么边界框重叠率S通常被刻画为S=其中⋃、⋂表征两个子区域像素的并集、交集,|∙|指像素点的统计数目。为度量追踪器总体性能,需要统计重叠S不小于指定阈值t0时的成功帧的数目。成功率图(Success Plot)上,跟踪成功视频帧所占比率取值0至1。新近比较主流的一个指标是曲线下方面积(Area under Curve,AUC)[3],本文也将根据AUC曲线对追踪器进行性能度量及排序。
上面两种度量方法都是根据基准目标的坐标对第一帧进行初始化,之后进行视觉跟踪得到精度和成功率。它们被统称作一次性评估(One-Pass Evaluation,OPE)[46]。它们存在两个主要不足:首先,特定跟踪器也许对第一帧的初始位置比较敏感,在不同位置或者不同帧对算法进行初始化可能对跟踪效果产生巨大的影响;其次,一些跟踪器丢失目标之后不设置重新初始化的机制。因此,又提出了以下多种测评方法:时间鲁棒性评估(Temporal Robustness Evaluation,TRE)[47]、空间鲁棒性评估(Spatial Robustness Evaluation,SRE)[48]、一次性重评估(One-Pass Evaluation with Restart,OPER)[49]、空间鲁棒性重评估(Spatial Robustness Evaluation with Restart,SRER)[50]。
接下来,本文将对WGCA跟踪器从时间鲁棒性和空间鲁棒性两个指标进行评估。时间鲁棒性评估(TRE)从不同的帧作为起始进行跟踪,初始化采用的边界框即为对应帧人工标注的边界框,最后对这些结果取平均值,得到TRE分数。空间鲁棒性评估(SRE)把人工标注框进行多尺度扩大与缩小和略微地平移来产生新的边界框。平移的距离通常取跟踪对象大小的10%,尺度变化的大小取人工标注框的70%至110%,依次增长10%,最终SRE分数被定义为它们的平均值。
4.2.2 参数设置
所有的基准跟踪器、自适应目标跟踪器和CA跟踪器均使用原作者提供的标准参数运行。为了公平比较,使用相同的参数运行WGCA跟踪器。将正则化因子λ2设置为{2,25,0.4,0.5},并对 MOSSEWGCA、DCFWGCA、SAMFWGCA和STAPLEWGCA分别使用学习率为{0.025,0.015,0.005,0.015}的更新规则。将上下文区域k的数量设置为9,并在目标周围均匀采样。为了增加全局上下文的鲁棒性,对所有WGCA跟踪器进行了填充。
本文的实验代码在CA框架开源的Matlab代码上进行改写而成[22],主要增加了基于光流跟踪算法的全局上下文权值矩阵计算模块。实验中所有的跟踪器都使用Matlab9.2进行编程实现并且在同一台PC(Intel®CoreTMi7-7820HQ CPU 2.90 GHz,16.0 GB RAM)上运行。
4.3 定量结果分析
4.3.1 整体评估
图4显示了OTB-100上所有基准跟踪器及其自适应目标的上下文感知和加权全局上下文感知算法对应的结果。WGCA框架改善了所有基准跟踪器的性能,随着使用更复杂的特征,性能反而会降低。对于复杂的CF跟踪器(SAMF)和基本的CF跟踪器(MOSSE),WGCA框架较CA框架精度相对改进为从{18.2%,3.6%}到{25.5%,11.0%},成功率的相对改进为从{13.1%,6.3%}到{28.5%,19.0%}。此外,WGCA框架不仅超越基准,而且超过相应的AT追踪器(不适用于STAPLE[20])和CA跟踪器。与自适应目标框架相比,这种性能增益的计算成本要低得多。WGCA框架跟踪器的运行速度约为基准的60%,但比AT版本的速度快1.3~2.0倍,与CA框架算法的运行速度相当。

图4 跟踪器在OTB-100上的平均总体性能
表2展示了16个视觉跟踪算法跟踪的中心位置误差(CLE)和帧率(FPS),这些算法分别是MOSSE、DCF、SAMF、STAPLE、MOSSECA、DCFCA、SAMFCA、STAPLECA、MOSSEAT、DCFAT、SAMFAT、WSTC、MOSSEWGCA、DCFWGCA、SAMFWGCA、STAPLEWGCA。从表中可以发现,本文WGCA跟踪器在OTB-100测试集的4个视频Jumping、Human7、Car1和Skiing上均取得了最佳的跟踪结果。同时,虽然基于CA框架的跟踪器也有较高的准确率,但是对于以上4个视频集成WGCA框架的跟踪器在牺牲较小效率的前提下,较CA框架跟踪器的CLE分别降低了40.7%、35.0%、45.7%、46.9%。
4.3.2 运算效率评估
只从跟踪帧率方面分析,上述改进跟踪器的目标检测速率都较基准跟踪器有不同程度的降低,但是这并未考虑它们在跟踪精度方面带来的效果提升。因此,下面考虑通过帧率误差比C来评估跟踪算法的运算效率。帧率误差比C定义为C=FPS/CLE,其中FPS为视觉跟踪器的平均帧速率,CLE表示中心位置误差。帧率误差比C综合考虑了跟踪器的运算速度指标FPS和跟踪精度指标CLE对跟踪算法性能的影响,是一个较好的视觉跟踪算法运算效率评估指标。
图5给出了4个基准跟踪器,基于CA框架的目标跟踪器以及本文WGCA跟踪器的帧率误差比。从图中可以看出,WGCA算法对4个基准跟踪器的运算效率提升均是最大的。但是随着基准跟踪器复杂性的增加,运算效率提升的增益降低,出现这种情况因为后两个跟踪器采用了多尺度[22-23],WGCA框架对它们运算效率提升相对有限。基于CA框架的跟踪器相对于基准跟踪器运算效率也有所提升,然而本文WGCA框架采用了求闭式解的方法,并且在实施Lucas-Kanade稀疏光流跟踪时使用Harris角点作为特征点进行快速计算,整体在运算效率方面更加具有优势。

图5 跟踪器运算效率比较图
4.3.3 按属性评估
本文提出的WGCA框架在大多数情况下提高了基准跟踪器的性能,并在某些情景下比其他情景获得了更大的改进。在快速运动(图6(a))、运动模糊(图6(b))、遮挡(图6(c))和比例变化(图6(d))的情况下,跟踪器的性能得到了显著的改进。其中,快速运动指目标的运动速度大于阈值;运动模糊指目标区域由于目标或相机的运动而模糊;遮挡指目标部分或完全遮挡;比例变化指第一帧和当前帧边界框之比大于1。特别地,如果对象外观急剧变化(例如比例变化、遮挡)或者背景与目标相似(例如背景模糊)的情景,WGCA框架非常有效。此外,它在具有快速运动的视频中也显著提高了跟踪器的性能。这主要是由于添加加权全局上下文充分利用了被搜索区域的信息。同样值得注意的是,在大多数情况下,本文方法优于自适应目标框架[22],该框架是专为提高快速运动场景跟踪器的性能而设计的。
4.3.4 鲁棒性评估
为了验证本文提出的WGCA框架的鲁棒性,采用时间鲁棒性评估(TRE)和空间鲁棒性评估(SRE)两个评价标准进行度量。实验中将具有最佳性能的加权全局上下文感知CF视觉跟踪器(SAMFWGCA和STAPLEWGCA)及其基准(SAMF[23]和STAPLE[20])与新近提出的跟踪器SOWP[51]、HCFT[52]和 MEEM[53]进行了比较。此外,还选择了不符合WGCA框架的目前主流CF跟踪器DSST[54]、MUSTER[55]、SRDCF[13]进行对比分析。DSST 与 SAMF非常相似,MUSTER采用长短期内存策略,SRDCF在最近的跟踪基准测试中[13]排名第一,但不适用于WGCA框架。最后,与TLD[56]和经典上下文跟踪器CXT[19]进行比较。如图7所示,本文提出的STAPLEWGCA跟踪器依然是这些视觉跟踪算法中鲁棒性最优的。

表2 中心位置误差(CLE)和帧率(FPS)

图6 跟踪器在OTB-100中4个属性的平均性能
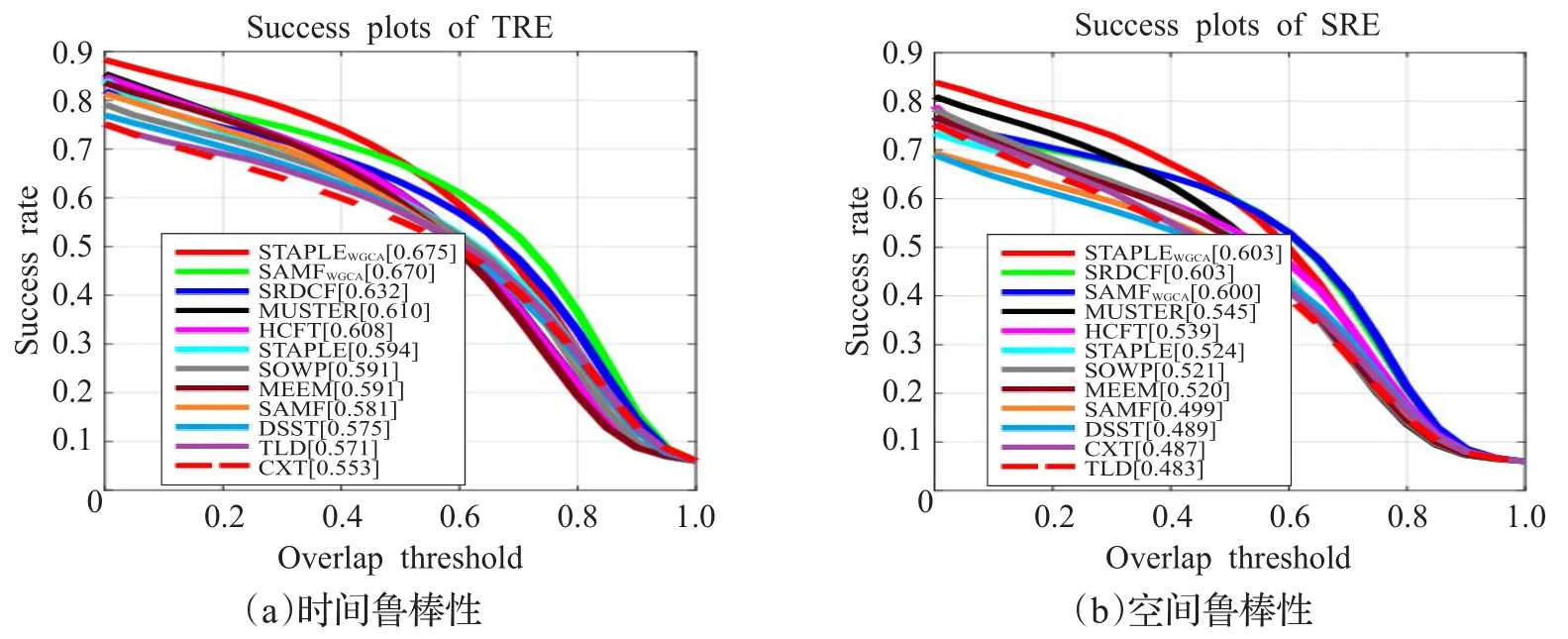
图7 跟踪器在OTB-100上的鲁棒性评估
4.4 定性结果展示
为了可视化本文提出的WGCA框架在跟踪性能方面的效果,在图8和图9中展示了4个基准算法MOSSE、DCF、SAMF、STAPLE与其对应的加权全局上下文感知跟踪算法 MOSSEWGCA、DCFWGCA、SAMFWGCA、STAPLEWGCA对来自OTB-100中的多个示例视频进行跟踪比较的例子。大体上,这些视频主要包括两个场景:快速运动(Fast Motion)以及遮挡(Occlusion)。
从上述包含快速运动和遮挡两个主要场景视频的跟踪效果图上可以直观地发现,本文提出的WGCA框架能够追踪到目标,并且没有出现明显的偏移或目标丢失的现象。同时,基于WGCA框架的CF跟踪器明显地提高了相应基准跟踪器的视觉跟踪精度。

图8 OTB-100中包含Fast Motion的部分视频跟踪效果图
图8主要包含快速运动场景。第1行给出了视频Car2的跟踪效果图,从#228帧、#368帧、#549帧、#793帧、#901帧可以明显看出基准跟踪器出现了不同程度的偏移现象;第2行视频Crossing的#5帧、#35帧、#78帧、#110帧、#120帧基准跟踪器依然出现了偏移;第3行视频Surfer的#9帧、#72帧、#113帧、#177帧、#236帧基准跟踪器由于人的快速移动出现了目标丢失的现象,由于WGCA框架可以利用人体上下文信息,其依然可以实现对目标对象的鲁棒跟踪;第4行视频Couple的#69帧由于车辆的出现,基准跟踪器出现了偏移现象,#113帧由于人快速移动以及背景的改变,基准跟踪器出现了偏移和目标丢失的现象。
图9主要包含遮挡场景。第1行给出了视频David3的部分跟踪结果,#86帧、#190帧、#240帧中人在被路标指示杆或树遮挡的情况下,基准跟踪器出现了偏移甚至跟丢目标的现象;第2行视频Jump包含遮挡、快速移动、比例变化、背景模糊、复杂背景、目标旋转等多种因素,从#10帧、#42帧、#51帧、#72帧、#88帧可以看出,即使基准跟踪器把目标跟丢,WGCA跟踪算法依然能够准确地跟踪到目标对象;第3行视频Skating1含有遮挡、背景复杂等场景,从#6帧、#154帧、#158帧、#167帧、#308帧可以发现,基准跟踪器跟踪结果出现较大偏差,但基于WGCA框架的算法的跟踪效果并没有受到影响;第4行视频Walking2包含遮挡、比例变化、低分辨率等因素,受此影响在#190帧、#204帧、#223帧、#371帧图像上基准跟踪器出现了丢目标的现象,WGCA框架的跟踪器由于充分利用了上下文信息,跟踪效果依然非常好。
4.5 进一步讨论
根据滤波器的单通道、多通道特征和原始域、对偶域的不同组合,运算系统的复杂性以及求解的最佳方法会有所不同。但是,仔细选择矩阵求逆方法对于保持计算效率非常重要(参见3.5节)。
此外,本文提出的WGCA框架还可以揭示目标跟踪过程中何时可能发生潜在的跟踪故障。通常,数据项的能量可以用于表示帧与帧之间差异大小的指标。直观地说,这种能量从一帧到另一帧的剧烈变化可能表明跟踪器出现漂移的情况,但是在实际中这可能不是产生这种变化的唯一原因。例如,由于光照变化、变形、遮挡等,该能量也可能在几帧内突然波动。因此,单独的数据项不是目标漂移的可靠度量。另一方面,式(7)给出的上下文项的能量也可以用来表征数据项的影响。在许多情况下,目标的外观变化不会影响上下文(例如比例变化、变形、遮挡等),因此几个帧内的两个指标(数据项和上下文项)的突然变化是跟踪失败或漂移的更可靠度量指标。在视觉跟踪过程中综合考虑上述两个指标的作用可能有助于相关滤波跟踪器从跟踪故障中恢复过来。
5 结束语
本文提出了一个基于相关滤波器的视觉跟踪通用框架WGCA,该框架以较低的计算代价将全局上下文整合到滤波器训练阶段。主要思想为根据上下文中不同区域与追踪目标运动相似度大小,把上下文分成4类:目标区域、支撑区域、无关区域及干扰区域。采用光流法计算得到全局上下文权值矩阵,整合到CA框架的数据矩阵中,从而得到本文最终的WGCA框架。该框架可以轻松地与大多数CF跟踪器进行集成,可以充分发挥支撑区域的作用,同时降低干扰区域的影响,实现了鲁棒视觉跟踪的目标。大量实验表明,WGCA框架改善了所有测试的CF跟踪器的跟踪性能,并且拥有较高的计算效率。同时,通过实验进行评估,得出了WGCA框架最有效的几个场景:全部或部分遮挡,比例变化,背景模糊,快速运动。下一步研究将从以下两方面进行:融合目标自适应框架;采用深度学习的方式对上下文环境进行特征提取,以得到对全局上下文更加精确的权值矩阵表示。
