格蕴涵代数中的极小素理想及α-理想

孟彪龙，付巧峰，梁少辉

MENG Biaolong,FU Qiaofeng,LIANG Shaohui

西安科技大学 数学系，西安 710054

Department of Mathematics,Xi’an University of Science and Technology,Xi’an 710054,China

1 引言

为了研究命题真值取值于格上的逻辑系统，徐扬等[1-2]将格和蕴涵代数相结合，提出了格蕴涵代数。王国俊[3]证明了格蕴涵代数与MV-代数范畴等价。理想/滤子是格蕴涵代数的一类重要子结构，是刻画格蕴涵代数的一个重要工具。自格蕴涵代数提出后，诸多学者对格蕴涵代数的理想/滤子理论做了大量的研究工作。例如，Jun[4]提出了格蕴涵代数中的LI-理想并得到了ILI-理想的扩张原理。刘用麟等[5]、朱华等[6]相继提出了格蕴涵代数的素理想、极大理想和准素理想等并讨论了它们之间的关系等。赵建斌等[7]提出了格蕴涵代数中的零化子，给出其初步性质。孟彪龙[8]和Jun[9]分别引入格蕴涵代数的素滤子并证明了素滤子定理。朱华等[10]在格蕴涵代数中提出扩张滤子并用之刻画了素滤子。α-理想是Cornish[11]在分配格中提出并用之对广义Stone格进行了刻画。之后，Jayaram等[12-15]进一步将此概念推广到0-分配格、C-代数等并研究了其性质。Zou等[16]提出了BL-代数的α-理想并证明其等价于对合理想，继而研究了α-理想集合的代数结构。本文进一步研究格蕴涵代数中的极小素理想，讨论极小素理想与极小格素理想的关系以及极小素理想与零化子的相互表示问题。引入格蕴涵代数中的α-理想并讨论其性质和等价刻画。最后研究全体素α-理想之集Sα(L)的拓扑性质。

2 预备知识

定义1[1]设(L,∧,∨,')是一个有泛界0,1的有余格，≤是L上的偏序关系。若映射→:L×L→L满足：

∀x,y,z∈L

(I1)x→(y→z)=y→(x→z)；

(I2)x→x=1；

(I3)x→y=y′→x′；

(I4)若x→y=y→x=1，则x=y；

(I5)(x→y)→y=(y→x)→x；

则称(L,∧,∨,'→,0,1)是一个拟格蕴涵代数。若它还满足：

(I6)(x∨y)→z=(x→z)∧(y→z)；

(I7)(x∧y)→z=(x→z)∨(y→z)；

则称(L,∧,∨,'→,0,1)是一个格蕴涵代数。

下文中，L始终表示一个格蕴涵代数。

定义2[2]设I是L的非空子集。若I满足：（1）0∈I；（2）(x→y)′,y∈I蕴涵x∈I，则称I是L的一个理想。

设I是L的一个真理想。若∀x,y∈L,x∧y∈I蕴涵x∈I或y∈I,则称I是L的一个素理想（见文献[4]）。L的全体理想之集记为I(L)，显然I(L)是一个完备分配格，其中对I(L)的任一非空子集{Ii|i∈Λ} ，∧i∈ΛIi=⋂i∈ΛIi，∨i∈ΛIi=(⋃i∈ΛIi]，后者表示由{Ii|i∈Λ} 所生成的理想。又记L的全体素理想之集为PI(L)。

定理1[2，17]设A是L的非空子集。由A生成的理想记为(A]，则：

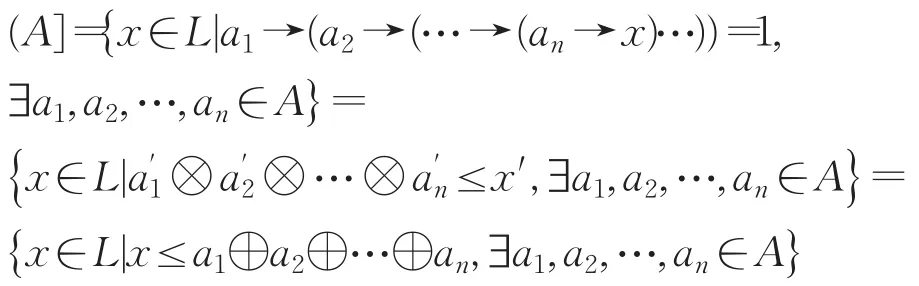
其中，a⊗b=(a→b′)′，a⊕b=a′→b。

定义3[7]设B是L的非空子集，则集合B*={x∈L|称为B的零化子。当B={a}时，简记为a*。

定理2[6]设B、C是L的非空子集，则下列性质成立：

（1）B*∈I(L)且(B]*=B*；

（2）B⊆C⇒C*⊆B*；

（3）B⊆B**，B*=B***；

（4）(B⋃C)*=B*⋂C*；

（5）若B∈I(L)，则B⋂B*={0}。

3 格蕴涵代数上的（极小）素理想

命题1 设I,J∈I(L)，记I→J={x∈L|(x]⋂I⊆J}，则下列结论成立：

（1）I→J∈I(L)且I⋂(I→J)⊆J；

（2）I⋂K⊆J当且仅当K⊆I→J。

其中K∈I(L)。

证明 仅证（1）显然0∈I→J。若(x→y)′,y∈I→J则 ((x→y)′]⋂I⊆J，(y]⋂I⊆J。由I(L)是分配格知(((x→y)′]∨(y])⋂I=(((x→y)′]⋂I)∨((y]⋂I)⊆J。又由(x→y)″→(y′→x′)=(x→y)→(x→y)=1 ，因 此x∈((x→y)′]∨(y]且 (x]⋂I⊆(((x→y)′]∨(y])⋂I⊆J，所以x∈I→J，此即说明I→J是L的理想。又 ∀x∈I⋂(I→J)，由x∈I→J知(x]⋂I⊆J。又由于x∈I，因此x∈(x]⋂I⊆J,x∈(x]⋂I⊆J,蕴涵I⋂(I→J)⊆J成立。

由上述命题知，I(L)是一个完备的Brouwer格，其中∀I,J∈I(L)，I→J是I关于J的相对伪补元。特别地，I→{0}=I*是I的伪补元。

命题2设P∈PI(L)且P*非零，则∃a∈LP使得P=a*。

证明 若P*≠{0}，则 ∃a∈P*且a≠0，由定理2（3）则有P⊆P**⊆a*。若x∈a*，x∧a=0∈P，又由P是素的知x∈P或a∈P。若a∈P，则a∈P⋂P*={0}，与a≠0矛盾。故x∈P，a*⊆P。综上知P=a*，命题成立。

命题3 若 ∀P∈PI(L)有P*非零，则 ∀I,J∈I(L)，I⋂J={0}⇒I*∨J*=L。特别地，∀I∈I(L)，I*∨I**=L。

证明 假设 ∃I,J∈I(L)使得I⋂J={0}，但I*∨J*⊂L，则∃a∈L(I*∨J*)，于是由格蕴涵代数的素理想定理（见文献[4]）知∃P∈PI(L)使得I*∨J*⊆P且a∉P。由定理2（2）和I(L)是Brouwer格知P*⊆I**,J**⇒P*⊆I**⋂J**=(I⋂J)**={0}，与P*非零矛盾，因此命题成立。又∀I∈I(L)，显然I⋂I*={0}，因此I*∨I**=L。

定理3若∀P∈PI(L)有P*非零，则I(L)是一个Stone格。

所谓Stone格即满足Stone恒等式x′∨x″=1的伪补分配格，其中x′是x的伪补元（见文献[18]）。

定义4设P是L的一个素理想（格素理想）。若对任意的素理想（格素理想）J，J⊆P蕴涵J=P，则称P是L的一个极小素理想（极小格素理想）。

定理4设I是L的一个真的格理想。∀a∈L，记Ia={x∈L|(a→x)′∉I}，K(I)=⋂{Ia|a∈LI}，则K(I)是L的一个理想且K(I)⊆I。特别地，如果I是L的一个格素理想，则K(I)也是L的一个素理想。

证明 显然 0∈K(I)。设 (x→y)′,y∈K(I)，则由(x→y)′∈K(I)知 ∀a∈LI，(x→y)′∈Ia，即 (a→(x→y)′)′∉I。由y∈K(I),则y∈I(a→(x→y)′)′,即((a→(x→y)′)′→y)′∉I。由于

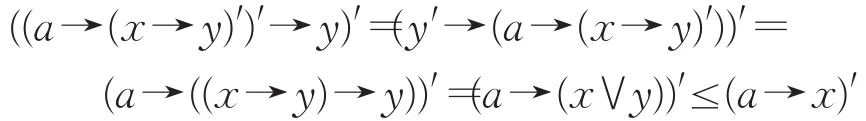
因此(a→x)′∉I，x∈K(I)，此即说明K(I)是L的一个理想。又∀a∉I，由(a→a)′=0∈I，因此a∉Ia，继而有a∉K(I)，故K(I)⊆I。

假设I是L的一个素理想，现证明K(I)也是L的一个素理想。首先说明下列事实：

（1）设J是L的一个真格理想，则∀a∈L，x∧y∈Ja蕴涵x∈Ja或y∈Ja。

事实上，若x∧y∈Ja，则(a→(x∧y))′∉J。又由于(a→x)′∨(a→y)′=((a→x)∧(a→y))′=(a→(x∧y))′,则由J是格理想知(a→x)′∉J或(a→y)′∉J，结论成立。

（2）若J是L的一个真格理想，则∀a,b∈L,Ja∧b⊆Ja⋂Jb。 ∀z∈Ja∧b,则 ((a∧b)→z)′∉J。由于 ((a∧b)→z)′=(a→z)′∧(b→z)′，于是由J是格理想知 (a→z)′∉J且 (b→z)′∉J，即z∈Ja且z∈Jb，因此有Ja∧b⊆Ja⋂Jb。

设x,y∉K(L)，则∃a,b∉I使得x∉Ia,y∉Ib。由I是素理想知a∧b∉I。又如果x∧y∈K(I)，则x∧y∈Ia∧b，由（1）知x∈Ia∧b或y∈Ia∧b，继而由（2）知x∈Ia或y∈Ib，矛盾。因此x∧y∉K(I)，即说明K(I)是素理想。

推论1设P是L的一个真理想，则P是L的极小素理想当且仅当P是L的极小格素理想。

定理5设P∈PI(L)，则P是L的一个极小素理想当且仅当∀a∈P，∃b∈LP使得a∧b=0。

证明 仅证必要性：首先由推论1知P是L的一个极小格素理想。取a∈P，记F={x∈L|∃y∈LP:a∧则易证F是L的一个格滤子且a∈F。又显然LP⊆F，现证下列结论成立：

(*)若0∉F，则存在L的一个格素理想M使得M⋂F=∅。

记与F不交的L的格理想之集为S，由0∉F知S≠∅。又由Zorn's引理知S有极大元M。若M不是格素理想，则 ∃x,y∉M但x∧y∈M。记x、y分别与M生成的格理想为＜M⋃x＞，＜M⋃y＞，由M是S的极大元知＜M⋃x＞⋂F≠∅,＜M⋃y＞⋂F≠∅，故∃r,s∈M使得r∨x∈F,s∨y∈F,由F是格滤子知(r∨x)∧(s∨y)∈F。又由L是分配格，则：

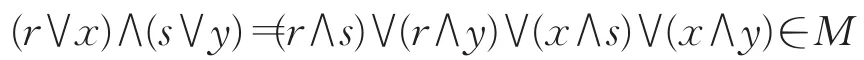
于是有M⋂F≠∅，矛盾。因此M是L的一个格素理想，且M⋂F=∅，(*)成立。

由LP⊆F和(*)知M⊆P且a∈PM,与M是极小格素理想矛盾，故0∈F,即∃b∈LP使得a∧b=0,命题得证。

推论2设P是L的一个极小素理想，则P=⋃x∉Px*。

下面给出零化子的一个表示定理。

定理6设a∈L，则a*=⋂{P|P是极小素理想且a∉P}。

证明 记W=⋂{P|P是极小素理想且a∉P}。设P是一个极小素理想且a∉P,则∀x∈a*，x∧a=0∈P。由P是素的且a∉P知x∈P蕴涵a*⊆P，因此a*⊆W。反之，若x∉a*,则存在素理想P0使得x∧a∉P0，因此x∉P0。记不包含x的素理想之集为B，则由对偶Zorn's引理知B有极小元Q且x∉Q，因此x∉W，W⊆a*，命题成立。

由于 ∀I∈I(L)，I*=⋂x∈Ix*，结合定理6则下述结论成立。

推论3设I∈I(L)，则I*=⋂{P|P是极小素理想且I⊄P}。

定理7设P∈PI(L)，则P是极小素理想当且仅当∀x∈L，x、x*有且仅有一个属于P。

证明 设P是极小素理想，则显然x、x*至少有一个属于P。又若x∈P，由定理5知∃y∉P使得x∧y=0即y∈x*，因此y∈x*P，x*⊄P。若x*⊆P，则显然x∉P，否则∃y∉P使得y∈x*蕴涵y∈P，矛盾。反之，若Q∈PI(L)且Q⊂P，则∃x∈PQ。由题设知x*⊄P，继而有x*⊄Q，于是有y∈x*Q。由Q是素理想知x∧y∉Q，由y∈x*又知x∧y=0，于是有0∉Q，矛盾。因此P是极小素理想。

推论4设P∈PI(L)，若P是极小素理想，则∀x∈L，x∈P当且仅当x**⊆P。

证明 设x∈P，y∈x**P。由定理7知x*⊄P，则∃a∈x*P。由P是素理想知y∧a∉P⇒y∧a＞0，而由y∈x**和a∈x*知y∧a=0，矛盾，故x**⊆P。又x**⊆P显然蕴涵x∈P，故命题成立。

设I∈I(L)，若I**=I，则称I是L的一个对合理想。由推论3知下列结论成立。

推论5设I是L的一个对合理想，则I=⋂{P|P是极小素理想且I⊆P}。特别地，L的所有极小素理想之交为{0}。

定理8设∀I∈I(L)L且I*非零，则下列条件等价：

（1）每个理想是对合理想；

（2）每个素理想是对合理想；

（3）(PL(L);⊆)是反链。

证明 (1)⇒(2)显然。

(2)⇒(3)不妨设P,Q∈PI(L)且P⊂Q，则 ∃a∈QP。又∀b∈Q*，则显然a∧b∈Q⋂Q*={0}⊆P。由于a∉P且P是素的，因此b∈P⊂Q，故而b∈Q⋂Q*={0}蕴涵Q*={0}。由题设Q是对合的，则有Q=与Q是真理想矛盾。因此，P⊄Q，故（3）成立。

(3)⇒(1) ∀I∈I(L),I⊆I**成立。又a∈I**,则(a]⊆I**⇒I*=I***⊆(a]*=a*。若a∉I，则 ∃P∈PI(L)使得I⊆P，a∉P，于是P*⊆I*。由a∉P则有(a]⊄P，又由(a]⋂(a]*={0}⊆P和P是素的知a*=(a]*⊆P。由题设有 (a]∨P=L,因此 (a]*⋂P*=((a]∨P)*=L*={0}。又由I*⋂P*⊆(a]*⋂P*⇒P*=I*⋂P*={0}，矛盾。因此a∈I，即I**⊆I。综上知I**=I，（1）成立。

4 格蕴涵代数上的α-理想

定义5设I∈I(L)。若∀a∈L，a∈I蕴涵a**⊆I，则称I是L的一个α-理想。

显然，{0}和L都是α-理想。

例1[6]设L={0,a,b,c,d,1}是图1所示的偏序集。定义L上的“′”运算为：0′=1,a′=c,b′=d，c′=a，d′=b，1′=0 。L的蕴涵运算“ → ”见表1，则 (L,∧,∨,'→,0,1)是一个格蕴涵代数。

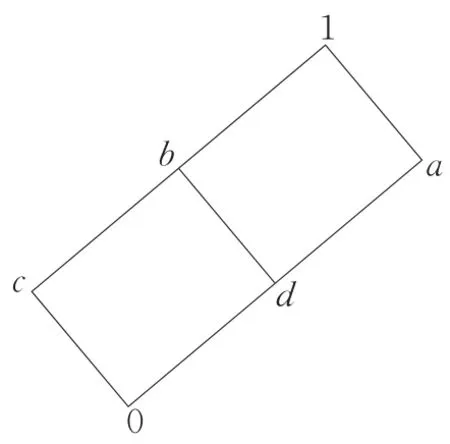
图1 L的偏序集

表1 L的“→”运算

I={0,d,a}是L的一个理想。验证可知a*=d*={0,c},a**=d**={0,d,a}，因此I是L的一个α-理想。

命题4L的对合理想是α-理想。特别地，若B⊆L非空，则B*是L的一个α-理想。

设I∈I(L),记，则下列结论成立。

定理9 设I∈I(L)，则α(I)是包含I的最小α-理想。

证明 显然I⊆α(I)。由0*=L知0∈α(I)。假设(x→y)′,y∈α(I)，则∃i,j∈I使得i*⊆((x→y)′)*,j*⊆y*。又 ∀t∈(i∨j)*，由 (t∧i)∨(t∧j)=t∧(i∨j)=0 知t∧i=0,t∧j=0 ，即t∈i*,t∈j*，于是有t∈((x→y)′)*,t∈y*，继而(x→y)′∈t*,y∈t*，由t*是理想知x∈t*蕴涵t∈x*，故而 (i∨j)*⊆x*，又显然i∨j∈I，因此x∈α(I)，即说明α(I)是L的理想。任取x∈α(I)，则 ∃i∈I使得i*⊆x*。又 ∀a⊆x**，则x*=x***⊆a*，因此i*⊆a*⇒a∈α(I)，所以有x**⊆α(I)即α(I)是L的α-理想。现假设J是包含I的任一α-理想。若x∈α(I)，则∃i∈I使得i*⊆x*，进而由x∈x**⊆i**，又由题设知i**⊆J，故x∈α(I)，α(I)⊆J，命题得证。

推论6设I∈I(L)，则下列命题成立：

（1）I是α-理想当且仅当α(I)=I；

（2）α(I)是包含I的所有α-理想之交；

（3）映射α:I↦α(I)是I(L)上的闭包算子。

命题5L的极小素理想是α-理想。

证明 设P是L的一个极小素理想，x∈P，则由定理5知∃y∉P使得x∧y=0,y∈x*。又由于∀z∈x**⇒x*⊆z*，因此y∈x*⊆z*蕴涵z∈z**⊆y*。由y∉P蕴涵(y]⊄P。若y*=(y]*⊄P，由P是素的则有0∈(y]⋂y*⊄P,矛盾，因此有y*⊆P。于是，z∈P,x**⊆P，P是α-理想。

命题6设P∈PI(L)且P*非零，则P是一个α-理想。

命题7设P是L的一个素理想，则I={x∈L|x∈a*:∃a∉P}是α-理想。

证明 显然0∈I。现假设(x→y)′,y∈I，则 ∃a,b∉P使得(x→y)′∈a*,y∈b*,进一步有(x→y)′,y∈(a∧b)*。由(a∧b)*是理想，则x∈(a∧b)*。又P是素的蕴涵a∧b∉P，故而x∈I，即I是理想。又∀x∈I，y∈x**，则∃a∉P使得x∈a*⇒a∈x*，于是y∧a=0，y∈a*，因此y∈I蕴涵x**⊆I，即I是一个α-理想。

类似可证下列结论成立。

命题8设F是L的一个格滤子，则I={x∈L|x∈a*:∃a∈F}是α-理想。

下面给出α-理想若干等价刻画。

定理10设I∈I(L)，则下列命题等价：

（1）I是α-理想；

（2）∀x,y∈L，x*=y*且x∈I蕴涵y∈I；

（3）I=⋃x∈Ix**；

（4）∀x,y∈L，V(x)=V(y)且x∈I蕴涵y∈I，其中V(x)是包含x的所有极小素理想之集。

证明 (1)⇒(2)显然。

(2)⇒(3) 若a∈⋃x∈Ix**，则存在x∈I使得a∈x**蕴涵a**⊆x****=x**，于是a**=a**⋂x**=(a∧x)**，继而a*=(a∧x)*。由x∈I知a∧x∈I，由题设（2）知a∈I，⋃x∈Ix**⊆I成立。又相反包含关系显然成立，（3）得证。

(3)⇒(1) 设a∈I，则由题设（3）知存在x∈I使得a⊆x**蕴涵a**⊆x**⊆I，故I是α-理想。

(2)⇒(4) 假设V(x)=V(y)。∀a∈x*,由定理6知a∈P,其中P是不包含x的任一极小素理想，于是P∈V(x)，a∉P。由V(x)=V(y)知∀P∈V(y),a∉P,所以a∈y*,x*⊆y*，因此x*=y*。反之假设x*=y*，若P是不包含x的任一极小素理想，则x*⊆P，由题设则y*⊆P。由P是极小素理想，继而由定理7知y∉P，此即P∉V(x)蕴涵P∉V(y)，因此V(x)=V(y)。

定理11设L是格蕴涵代数，则下列结论等价：

（1）每个理想是α-理想；

（2）每个主理想是α-理想；

（3）每个素理想是α-理想；

（4）∀x,y∈L，x*=y*⇒(x]=(y]。

证明 (1)⇒(2)显然。

(2)⇒(3) 设P∈PI(L)，又x∈P，则(x]⊆P。由题设知(x]是α-理想且x∈(x]，因此x**⊆(x]⊆P，即P是一个α-理想。

(3)⇒(4) 假设x*=y*且 (x]⊄(y]。记T={I∈I(L)|x∉I,x∧y∈I}，则(x∧y]∈T，故T≠∅ 。由 Zorn's引理知T有极大元P且是素的。否则∃s∉P,t∉P但s∧t∈P，于是P⊂(P⋃{s}]，P⊂(P⋃{t}]。由P的极大性知 (P⋃{s}]∉T，(P⋃{t}]∉T，于是由文献[3]定理3.17知x∈(P⋃{s}]⋂(P⋃{t}]=P，矛盾，因此P是素的，继而y∈P。由题设(3)知P是α-理想，又由定理10知x∈P，矛盾，命题成立。

(4)⇒(1) 设I∈I(L)，又若x*=y*且x∈I，则由（4）知y∈(y]=(x]⊆I，由定理10知I是L的一个α-理想。

下面讨论格蕴涵代数L的所有素α-理想之集Sα(L)的拓扑性质。

记S(x)={P∈Sα(L)|x∉P}，则易验证S(x)⋂S(y)=S(x∧y)，⋃x∈LSSα(L)，因此T={S(x)|x∈L}是Sα(L)的一个拓扑基。

命题9 设I∈I(L)是α-理想，∅≠S⊆L是∧-封闭的且I⋂S=∅，则存在L的一个素α-理想P使得I⊆P且S⋂P=∅。

命题10设L是格蕴涵代数，则∀x,y∈L，下列结论成立：

（1）S(x)=S((x])=S(x**)；

（2）S(x∨y)=S(x⊕y)=S(x)⋃S(y)；

（3）S(x**)⊆Sα(L)S(x*)。

命题11设A、B是L的非空子集。若⋂x∈AS(x)⊆⋃y∈BS(y),则存在A、B的非空有限子集A0,B0使得⋂x∈A0S(x)⊆⋃y∈B0S(y)。

证明 记A生成的格滤子为[A]，则[A]⋂α((B])≠∅。否则由命题9知∃P∈Sα(L)使得α((B])⊆P,[A]⋂P=∅。因此∀x∈A,y∈B，P∈S(x)，P∉S(y)蕴涵P∈⋂x∈AS(x),P∉⋃y∈BS(y),矛盾。现任取z∈[A]⋂α((B])，则由z∈[A]知 ∃a1,a2,…,an∈A使得a1∧a2∧…∧an≤z蕴涵S(a1)⋂S(a2)⋂…⋂S(an)=S(a1∧a2∧…∧an)⊆S(z)。

由z∈α((B])且(B]亦是一个格理想知∃b1,b2,…,bm∈B使得b≤b1⊕b2⊕…⊕bm且z∈b**，继而有z∈(b1⊕b2⊕…⊕bm)**，于是由命题10（1）和（2）知S(z)⊆S(b1)⋃S(b2)⋃…⋃S(bm),因此S(a1)⋂S(a2)⋂…⋂S(an)⊆S(b1)⋃S(b2)⋃…⋃S(bm)，命题成立。

推论7Sα(L)的一个开子集U是紧的当且仅当∃x∈L使得U=S(x)。

又Sα(L)显然是一个紧的T0-空间，结合命题11则下列结论成立。

定理12Sα(L)是一个Stone空间。

设M是L的一个α-理想，若M不包含于L的任一真α-理想中，则称M是L的一个极大α-理想。

定理13Sα(L)是一个T1-空间当且仅当每个素α-理想是极大的。

证明 ⇒:假设P是一个素α-理想但非极大的，则存在L的一个素的α-理想Q使得P⊂Q。由题设Sα(L)是T1-空间，则存在⋃S(xi)(i∈Λ)，⋃S(xj)(j∈τ)，其中Λ、τ是某两指标集，使得P∈⋃S(xi)⋃S(xj)，Q∈⋃S(xj)⋃S(xi)，因此存在i∈Λ,j∈τ，使得P∈S(xi)S(xj)，Q∈S(xj)S(xi)。由P∉S(xj)知xj∈P⊂Q，由Q∈S(xj)知xj∉Q，矛盾，因此P是极大的。

⇐:假设每个素α-理想是极大的。任取P,Q∈Sα(L)且P≠Q。由于P、Q是极大的，因此P⊄Q且Q⊄P，从而有a∈PQ,b∈QP蕴涵Q∈S(a)S(b)，故Sα(L)是一个T1-空间。

定理14若∀x∈L,有x*∨x**=L,则下列条件等价：

（1）Sα(L)是一个T2-空间；

（2）∀P,Q∈Sα(L)且P≠Q,则∃a,b∈L使得a*⊆P,b*⊆Q并且∀R∈Sα(L)，a∧b∈R。

证明 (1)⇒(2) 设P,Q∈Sα(L)且P≠Q,由Sα(L)是T2-空间，则P∈ ⋃i∈ΛS(xi),Q∈ ⋃j∈ΓS(yj)且(⋃i∈ΛS(xi))⋂(⋃j∈ΓS(yj))=∅，其中 Λ、Γ是某两指标集。于是 ∃i∈Λ,j∈Γ使得P∈S(xi)，Q∈S(yj)，S(xi)⋂S(yj)=∅ 。由知蕴涵于是就有，类似可证又若∃R∈Sα(L)使得xi∧yj∉R，则R∈S(xi)⋂S(yi)与其不交矛盾，命题（2）成立。

(2)⇒(1) 设P,Q∈Sα(L)且P≠Q,由题设∃a,b∈L使得a*⊆P,b*⊆Q。若a∈P,则a**⊆P蕴涵L=a*∨a**⊆P，与P是理想矛盾，故a∉P。类似可证b∉Q，故P∈S(a),Q∈S(b)。由题设显然S(a)⋂S(b)≠∅，因此Sα(L)是一个T2-空间。

5 结语

本文进一步研究格蕴涵代数中的极小素理想的性质，证明了极小素理想等价于极小格素理想，并给出了极小素理想与零化子的相互表示定理。提出了格蕴涵代数中的α-理想概念并给出其若干等价刻画，证明了极小素理想是α-理想。最后证明了素α-理想之集Sα(L)是一个紧的Stone空间，进一步给出Sα(L)分别是T1、T2拓扑空间的充要条件。