基于BP神经网络预测含腐蚀缺陷管道的极限压力

, ,

(1. 中国石油集团工程设计有限责任公司 北京分公司，海淀 100083； 2. 中国石油集团工程设计有限责任公司 西南分公司，成都 610017)

管道是油气资源长距离输送的主要工具，随着使用年限的增加,管道中累积的缺陷对管道的安全运行产生了巨大的威胁。其中腐蚀缺陷是管道最为常见的缺陷类型。为保证管道的安全性，国内外许多学者开展了含腐蚀缺陷管道剩余强度的分析与预测方法研究。帅健等[1]使用有限元方法对含腐蚀缺陷中低钢管道的剩余强度进行了分析，并基于大量有限元计算结果给出了管道极限压力的预测模型，同时分析对比了现有标准中腐蚀缺陷管道强度分析方法的优缺点[2]。王禹钦等[3]基于现有的标准给出了腐蚀管道剩余强度的评价方法。ZHU等[4]从理论上详细推导了含缺陷管道的强度计算方法，并对各种模型之间的差异进行了讨论。MA等[5]在帅健等人提出的模型基础上，给出了高强钢管道的极限压力预测公式。苏晨亮等[6-8]均使用有限元方法对不同载荷工况下的腐蚀管道进行了分析。现有的针对腐蚀管道极限压力的预测方法主要基于大量有限元数值计算结果与回归分析。这种方法需要大量的有限元数据，当使用条件改变时，需要重新进行大量的计算，成本较高。

本工作使用正交试验设计方法确定有限元计算的样本数量，综合考虑管道直径,壁厚,腐蚀缺陷长度、宽度、深度对管道极限压力的影响，使用非线性有限元方法计算得到不同情况下管道的极限压力，并使用BP神经网络进行管道极限压力预测，结果表明本方法计算成本低，需要计算样本数少，预测结果精度高。

1 含腐蚀缺陷管道的数值分析

1.1 管道应力应变模型

选用我国使用广泛的X70管线钢进行分析。图1给出了X70管线钢的真实应力-应变曲线，其应变性能较好，没有明显的屈服平台，屈服强度为485 MPa,抗拉强度为590 MPa。

图1 X70管线钢的真实应力-应变曲线Fig. 1 True stress-strain curve of X70 pipeline steel

1.2 有限元模型的建立

使用通用非线性有限元软件ANSYS建立有限元分析模型。埋地管道在一般状态下主要受到工作内压的作用，基于模型的对称性只需要建立1/4模型进行分析，如图2所示。管道使用四节点Solid单元划分，对缺陷附近网格进行细化，在其他部分网格划分较粗。由于建立的是对称模型，故需对缺陷处轴向截面和管道环向截面施加对称约束，对缺陷远端轴向截面施加轴向位移约束以模拟土壤对管道的轴向约束作用。计算过程中,在管道内壁施加管道工作内压，使用Newton-Raphson算法进行迭代计算。

图2 含腐蚀缺陷管道的有限元模型Fig. 2 Finite element model for pipeline with corrosion defects

1.3 管道失效准则的确定与验证

现有研究表明，高强钢管道爆破失效机理主要为材料塑性失稳导致的失效，取缺陷处应力达到抗拉极限作为管道失效准则较为合理。本工作也使用这一失效准则，并使用MA等的试验数据进行验证[5]，具体参数如表1所示。

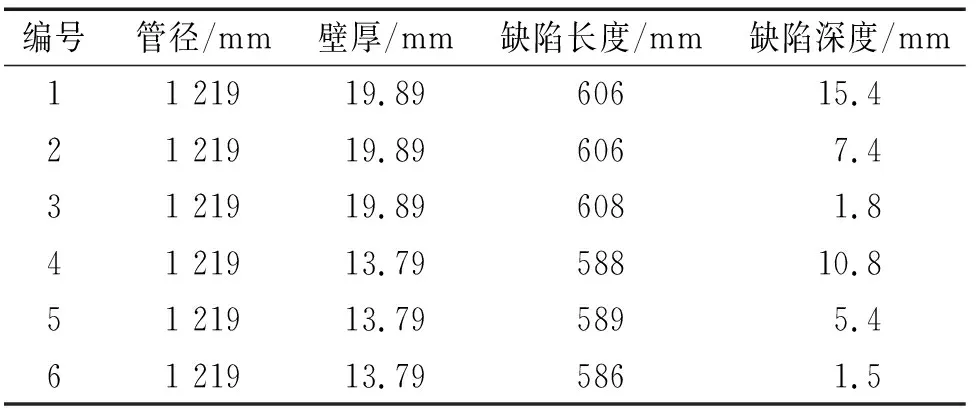
表1 含腐蚀缺陷管道的参数Tab. 1 Parameters of pipeline with corrsion defects

根据建立的有限元模型对管道极限压力进行计算，结果如图3所示，并与文献[5]有限元计算结果及其试验结果进行对比。可以得到，本模型计算结果与其余两者吻合较好，从而验证了本模型的准确性。

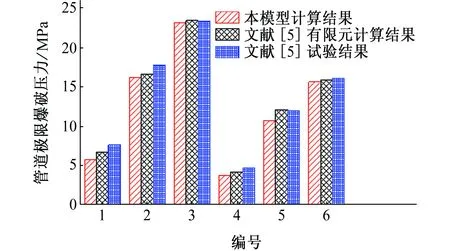
图3 本模型计算结果与文献[5]试验及其计算结果对比Fig. 3 Comparison of calculated results by proposed model with experimental and calculated results in reference[5]

2 基于正交试验方法的极限压力计算

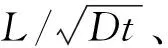
3 基于BP神经网络的腐蚀管道极限压力预测

3.1 BP神经网络基本原理

BP神经网络全称为误差反向传播多层前馈神经网络，是一种多层的感知器。BP神经网络包括了输入层、隐含层和输出层。按照隐含层的不同可分为单层BP神经网络和多层BP神经网络[10]。BP神经网络算法流程如图4所示。

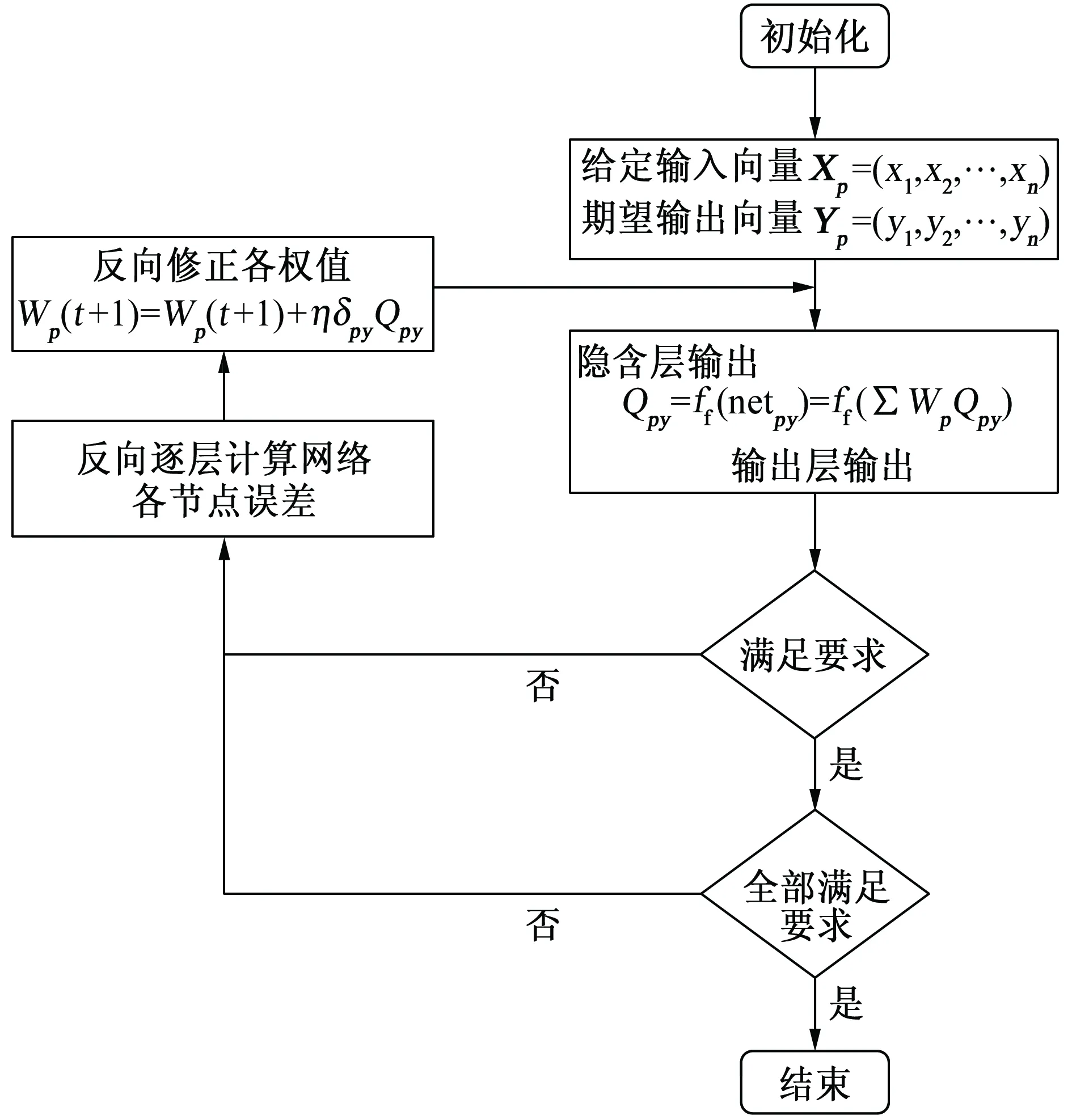
图4 BP神经网络训练流程Fig. 4 Training procedure for BP neural network

标准的BP算法收敛速度较慢，并且容易陷入局部极小值。因此，各种改进的算法被提出，如动量BP法。本工作使用广泛应用的Levenberg Marquardt法，该算法根据式(1)修正网络权值W。在工程应用中可以使用商用数值分析软件MATLAB调用trianlm训练函数进行BP网络训练。

W(n+1)=W(n)-[JTJ+μI]-1JTe

(1)

式中:J为包含误差性能函数对网络权值一阶导数的雅克比矩阵;e为网络总误差。

3.2 管道极限压力预测的BP神经网络

将管径、壁厚、无量纲腐蚀缺陷长度、无量纲腐蚀缺陷深度、无量纲腐蚀缺陷宽度这五个因数作为输入参数，将管道极限压力作为网络输出参数，根据Kolmogrov定理，建立的神经网络结构为5-11-1，中间层使用tansig型激活函数，输出层采用purelin型函数。图5为BP神经网络结构图。图6给出了BP神经网络训练结果与有限元计算结果的对比。从图6可以得到,经过多次训练后BP神经网络已经能够很好地描述这五种因素对极限压力的影响，两者吻合较好。

3.3 模型验证

为了更加科学地验证本模型的准确性，选择五种实际工程工况进行验证。表3给出了基于BP神经网络的预测结果和有限元计算结果，可以得到本模型预测结果较为准确，最大误差也仅为7.22%，从而表明本模型适用于一般工况条件下的腐蚀管道极限压力预测。

4 结论

开展了含腐蚀缺陷X70高强钢管道的极限压力预测方法研究。基于正交试验组合，综合考虑管径、壁厚，腐蚀缺陷深度、长度、宽度对管道极限压力的影响。并在此基础上给出了基于BP神经网络方法的管道极限压力预测方法。该预测方法能够在仅提供25组基础数据的情况下达到较好的预测精度，效率高。本方法可以为含腐蚀缺陷管道结构的剩余强度分析与安全评价提供一定的参考。

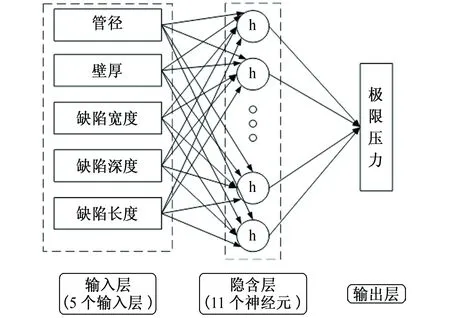
图5 预测管道极限压力的BP神经网络结构Fig. 5 BP neural network structure for predicting limit pressure of pipeline

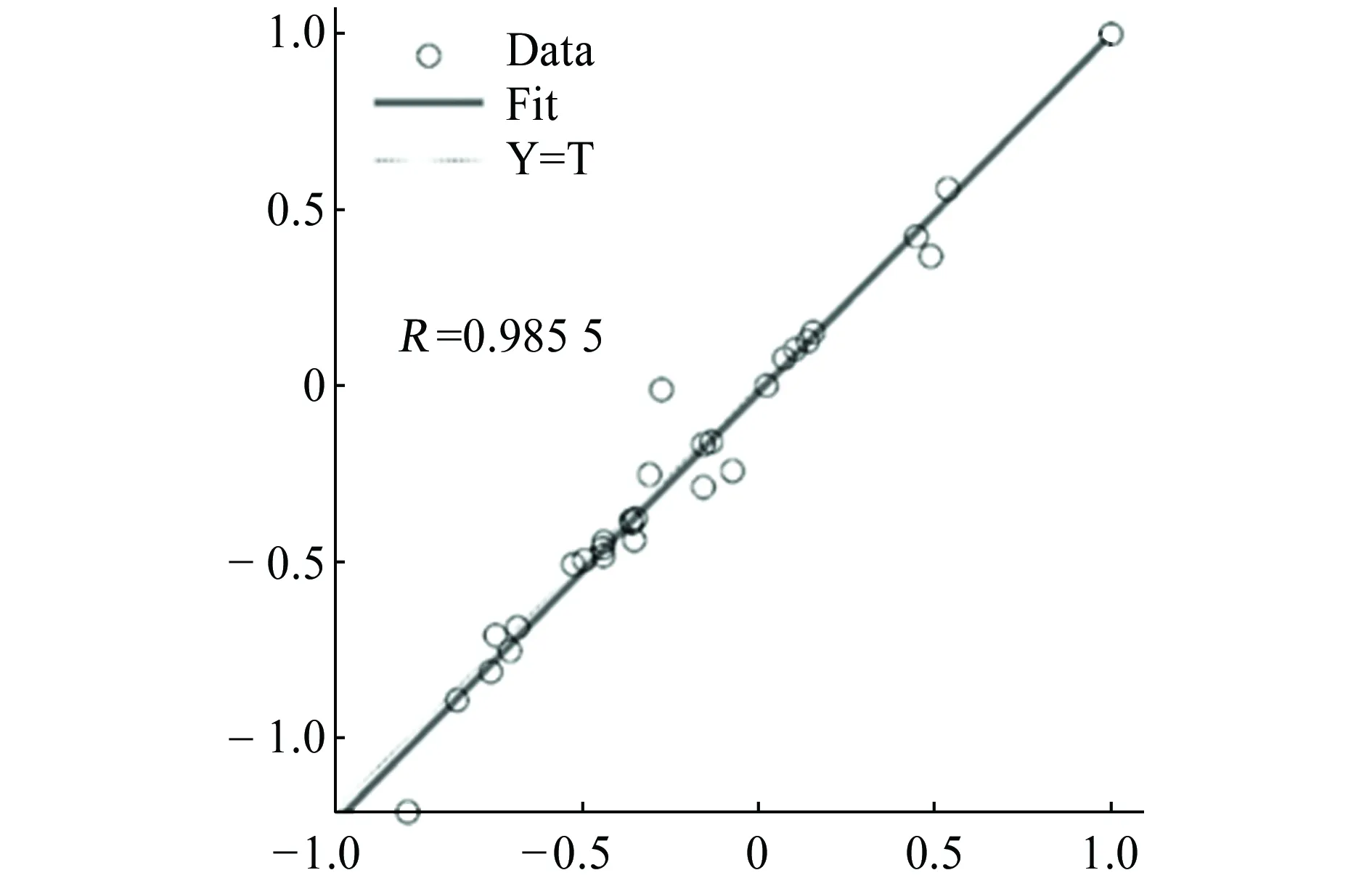
图6 BP神经网络训练结果与有限元计算对比Fig. 6 Comparison of training results of BP netural network and calculated results by finite element mothod

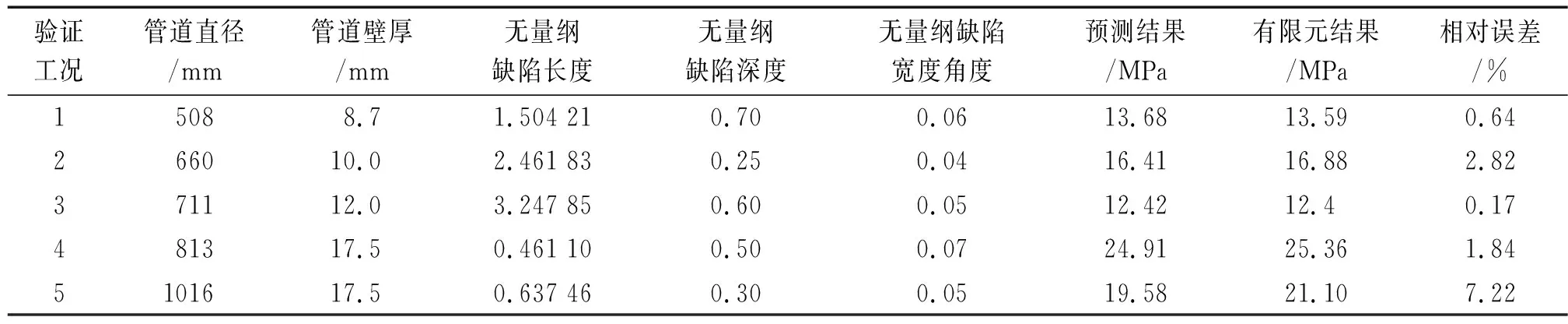
验证工况管道直径/mm管道壁厚/mm无量纲缺陷长度无量纲缺陷深度无量纲缺陷宽度角度预测结果/MPa有限元结果/MPa相对误差/%15088.71.504 210.700.0613.6813.590.64266010.02.461 830.250.0416.4116.882.82371112.03.247 850.600.0512.4212.40.17481317.50.461 100.500.0724.9125.361.845101617.50.637 460.300.0519.5821.107.22