误码及随机交织条件下信道编码类型识别
2018-08-20王伟年
王伟年 彭 华 董 政
(解放军信息工程大学,河南郑州 450002)
1 引言
在现代数字通信系统中,纠错编码技术常用来纠正随机独立错误,但是对于由多径衰落、同频干扰、脉冲干扰等造成的突发错误[1],纠错编码技术无法进行纠正。为抵抗突发错误,实际通信过程中往往会将纠错编码与数据交织技术进行级联。交织技术利用时间分集的思想,能够将连续突发错误离散成单个随机错误,使得纠错编码技术能够有效发挥作用,保证通信的可靠进行[2]。
在非合作通信领域,第三方截获到信号之后,首先就要进行解调得到比特流数据。然而,要想从信号层进入信息层,进一步获取有价值的信息,就必须进行信道编码分析[3],得到比特流数据的编码方式及参数,而其中交织参数识别分析是难点之一。
最常见的交织方式有矩阵交织[4]、卷积交织[5]和随机交织。矩阵交织和卷积交织均可以通过遍历交织参数进行识别,这里不再赘述。而随机交织识别比较困难,无法通过参数遍历方法解决,且目前已有的文献都是针对Turbo码中伪随机交织的识别,鲜有文献涉及包含Turbo码在内的非特定类型编码数据的随机交织参数识别。Turbo码中伪随机交织参数识别的方法主要有文献[6-9]:文献[6]提出了一种利用多样本数据逐位恢复交织的识别算法,首先对每个交织位置列出多个候选,计算由每个候选带给编码器的平均信息熵,然后设定合理门限对候选进行排除,最终得到整个交织关系;文献[7]提出了一种基于BCJR译码状态概率分布的方法,该方法假设前面i-1个交织关系已知,遍历求得各候选位置的状态概率,最大状态概率对应的位置即第i个交织位置;文献[8]利用SISO译码器软输出之间的互相关矩阵与交织矩阵的关系,并结合译码进行迭代,完成交织关系的识别。该方法抗误码能力较强,并且适用于任意交织方式;文献[9]提出一种基于校验方程平均符合度的识别算法。首先给出了校验方程平均符合度的定义,然后以校验方程平均符合度取到最大值为目标,逐步识别交织关系,最终得到整个交织关系。该算法不仅有较强的抗误码能力,且计算复杂度较低。
但上述算法要求编码结构已知,且信息序列和校验序列能够分开处理,而其他类型编码数据的随机交织通常是信息与校验全部进行交织,且编码结构完全未知,此情况下上述算法会完全失效。即上述算法仅适用于Turbo码的伪随机交织,对于其他类型编码数据的随机交织关系求解无法适用。针对此问题,本文提出一种基于搜索小重量向量的交织及编码类型识别算法:利用Canteaut-Chabaud算法[10]与LDPC译码进行迭代求得全部小重量校验向量,再通过所提出的两种统计量判断交织存在性及编码类型,即利用搜索得到的校验向量判断交织存在性及编码类型。交织后码字虽然信息与校验序列完全打乱,但校验关系依然存在,只是对应的位置发生了改变,所以可以将每个码字看成是定码长的分组码且校验向量可以搜索得到,再利用LDPC译码能够进一步降低码字误码率。由于使用软信息时LDPC译码效果更佳,所以本文后面进行译码时利用软解调序列。本文接下来的内容安排如下:第2节对误码条件下交织及编码类型识别问题进行描述;第3节介绍低重量校验向量搜索过程:Canteaut-Chabaud算法与LDPC译码进行迭代处理;第4节提出校验向量的两种度量,判断交织存在性以及编码类型;仿真实验结果在第5节中展示;末节将进行一些总结和讨论。
2 问题描述
本节描述基于软解调序列的交织及编码类型识别问题,发射端纠错交织结构如图1所示。
用ci表示交织前的码字,大小为1×n,hk表示交织前校验向量,大小为1×n,则有
(1)
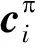
(2)
(3)
由式(3)可知,码字交织后的校验向量仅仅是1元素的位置发生了变化,校验向量数目完全没有改变,交织码字的约束关系依然稳定存在,因此仍可以从识别校验向量的角度出发对交织后的码字进行识别。本文的编码类型识别问题便是根据搜索得到的校验向量判断交织的存在性以及编码类型,为进一步识别交织关系提供依据。
为不失一般性,这里假设映射为简单的BPSK映射(0↔+1,1↔-1), 信道为加性高斯白噪声信道,则接收序列ri=zi+ei, 由于图1中省去了信号层面上的调制过程,因此软解调序列认为是接收序列ri,下面的所有过程均是基于软解调序列ri。
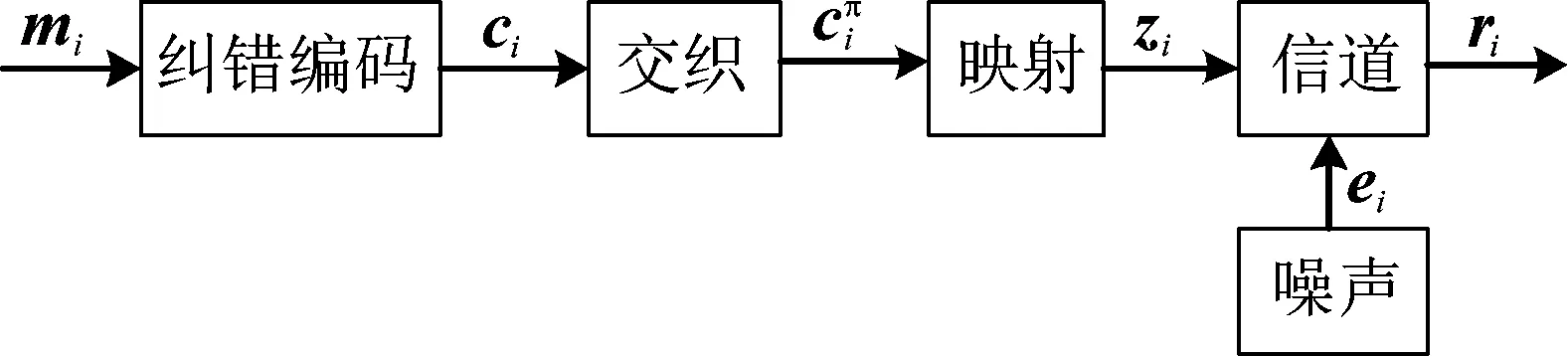
图1 发射端纠错交织结构
3 校验向量搜索
3.1 码字矩阵变换
假设接收到M帧码字序列r=(r1,r2,...,rM),其中ri=(ri,1,ri,2,...,ri,n)i=1,2,...,M,n代表每帧码字长度,相应的硬判决序列v=(v1,v2,…,vM),vi=(vi,1,vi,2,…,vi,n)。随机选取其中的N帧码字,组成矩阵G如下:
(4)
用R(X)表示由矩阵X的行向量张成的线性空间,用C表示由此N帧码字线性组合而成的码空间,则有R(G)=C;用H表示矩阵G的对偶矩阵(校验矩阵),则有
R(H)=C⊥=R(G)⊥
(5)
其中C⊥表示C在GF(2)n中的正交补空间,或称对偶空间(Dual Space)。
对G进行高斯约旦行消元以及列调换操作,可将其化简至系统形式的矩阵:
(6)
其中,k表示所选N帧码字中线性无关的码字数目。
利用式(6)可进一步可得到G的对偶矩阵的系统形式:
(7)
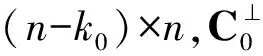
码字无误码时,H的行空间总是包含所有的校验向量,理论上能够从此空间中搜索出全部所需的校验向量,具体如下:
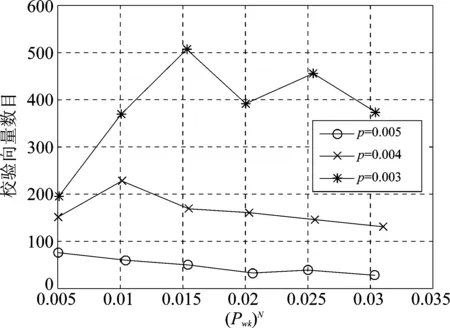
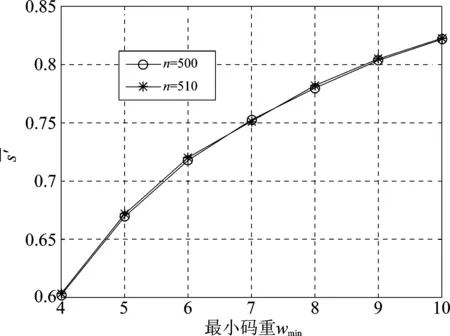
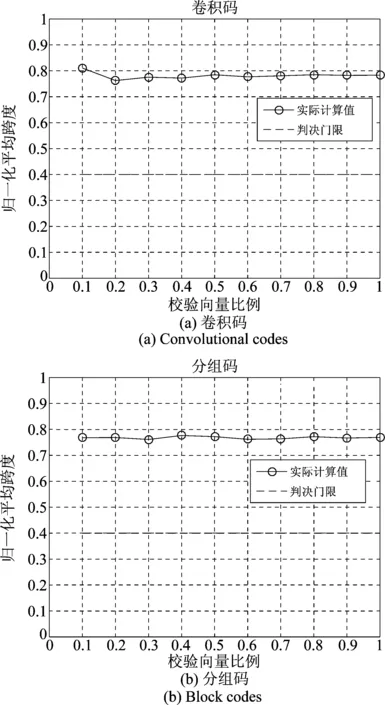
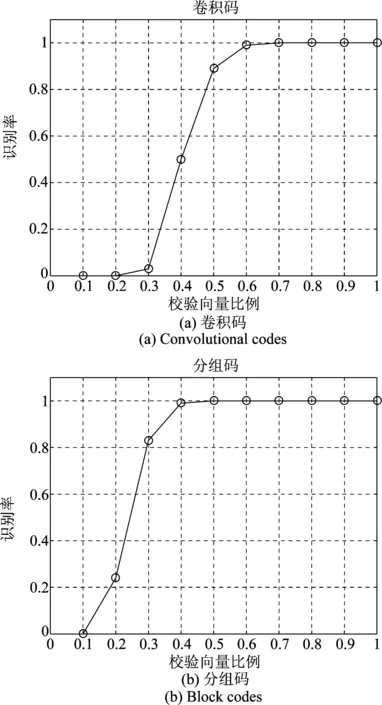
k k=k0时,R(G)=R(Gsys)=C=C0=R(G0) 3.2.1小重量向量搜索 从3.1节可知,校验向量可从H的行空间搜索得到,但当行空间的维数过高,空间中向量数目呈指数级增长,如何进行有效搜索就显得尤为重要。 (8) (9) 下面介绍比较经典的小重量向量搜索算法:Canteaut-Chabaud算法[10],该算法能够以迭代的方式快速找出输入系统矩阵行空间的小重量向量,具体如下: 信息列标号集合I,包含k+1,k+2,…,n共n-k个元素。 所有列标号集合S,重量阈值t,小重量向量集合Φ=∅,迭代次数Nc,1。 (3)从H1中随机选取p行,计算和向量s1,将取值s1|L添加至集合C1;从H2中随机选取p行,计算和向量s2,将取值s2|L添加至集合C2; (4) 考察集合C1、C2中所有满足s1|L=s2|L的(s1,s2)组合,若wt(s1|JL+s2|JL)≤t-2p,且h=s1+s2∉Φ,则令Φ=Φ∪{h}; 上述算法参数包括σ、p、t和Nc,1,σ、p选取方法已由文献[10]给出,这里不再赘述。由于实际编码数据中校验向量的重量都比较小,t可以取值小一些,这里取t≤10,Nc,1的选取可以根据计算量的限制进行进一步的设置。 3.2.2校验向量剔除 (10) (11) 3.2节已经得到部分有效校验向量,但数目较少且不同校验向量之间很可能存在线性关系,这样会对后面的识别产生不利影响,因此需要对校验向量进行精确搜索。 数目较少是码字存在误码所导致,因此必须首先降低码字的误码率。虽然码字存在交织,编码结构被完全打乱,但码字比特之间的约束关系仍然存在,已经搜索出的校验向量正是反映了这一点。而LDPC译码方法不要求编码方式必须是LDPC编码,只需校验向量已知,便可以根据校验关系进行有效译码,因此可以根据其原理对交织后码字进行译码。 传统的LDPC译码算法是基于Tanner图进行交叉处理,在每次迭代中都会多次涉及同一校验向量,计算复杂度较高;而专利[11]中的LDPC译码算法,由于对校验方程分开进行处理,每次迭代中仅涉及一次校验方程,因此计算复杂度较低。但两种方法译码性能基本相当,因此,本文采用专利[11]中的译码算法,在保证译码性能的同时有效降低了计算量。 校验向量之间存在线性关系会对第4节中的统计量产生不利影响,导致识别率降低,因此必须降低存在线性关系的可能性。3.2节已经搜索得到的校验向量码重都较低,但肯定存在最低码重,其他高码重校验向量很可能是由此低码重校验向量线性组合而来,因此在接下来的搜索中可以通过仅搜索最低码重的校验向量来降低存在线性关系的可能性。 由以上分析,校验向量精确搜索过程如下: (1)利用粗搜索得到的校验向量对码字进行LDPC译码; (2)利用粗搜索得到的校验向量确定最低码重tmin,令t=tmin,将Canteaut-Chabaud算法中第(4)步的判断条件wt(s1|JL+s2|JL≤t-2p修改为wt(s1|JL+s2|JL=t-2p; (3)粗搜索过程与LDPC译码进行迭代。 综合以上3小节的内容,可将校验向量搜索算法总结如下: 初始化: 接收码字总数目M,码长n,每次搜索选取码字数目N,Canteaut-Chabaud算法中迭代次数Nc,1,行数p=1,列数σ=10,重量阈值t,小重量向量集合Φ=∅。粗搜索过程中码字选取迭代次数Nc,2,LDPC译码与粗搜索过程迭代次数Nc,3。 (1)从M个码字中随机选取N个组成矩阵,变换至对偶矩阵Hsys; (2)利用Canteaut-Chabaud算法对Hsys行空间进行搜索,筛选剔除后得到部分有效校验向量,(1)(2)过程迭代进行Nc,2次,得到元素尽可能多的校验向量集合Φ; (3)利用集合Φ中元素对M个码字进行LDPC译码,并更新重量阈值t=tmin,去掉集合Φ中重量大于tmin的元素; (4)将Canteaut-Chabaud算法中wt(s1|JL+s2|JL)≤t-2p改为wt(s1|JL+s2|JL)=t-2p,重复前三个过程Nc,3-1次,得到最终的小重量校验向量集合Φ。 第3节已经搜索得到了大部分的校验向量,本节将对校验向量进行统计分析,根据统计量的结果判卷交织存在性以及编码类型。 实际通信中交织后的码字往往是由多个短码字合并到一起经过交织而成,因此交织后码字的校验向量始终能反映出原码的特点,通过找出并分析这些特点,能够确定编码类型,为交织关系分析提供依据。 这里提出校验向量的一种统计量:跨度S,代表校验向量中元素1位置的分布情况。设交织前码字校验向量hk中元素1的位置集合为{c1,c2,…,cwk},则hk的跨度Sk定义为 Sk=span(hk)=max{c1,c2,…,cwk}- min{c1,c2,…,cwk}+1 (12) (13) 若原码为分组码,则最低码重校验向量数目y满足 (14) (15) 对于原码为分组码,另有 (16) 从1,2,…,n中任取wmin个元素组成向量,其跨度为i,记Qi为跨度为i的选取方法总数目,则Qi满足 (17) (18) 从而可得到交织后校验向量的归一化平均跨度。 (1)更新Φ=ΦΦi,即从Φ中除去包含在Φi中的元素,执行步骤(2); (2)统计Φ中元素与Φi中元素是否有相同位置的1。若存在,则从Φ中剔除,添加至Φi,重复执行步骤(2);若元素不存在且Φ≠∅,则执行步骤(3);若Φ=∅,结束; (3)更新i=i+1,将Φ中第一个元素添加至Φi,执行步骤(1)。 经过以上步骤,可将校验向量集合Φ分为i个集合,各个集合之间的元素没有相同位置的1,可以认为各个集合之间相互独立。 这里将i的大小作为校验向量集合的一种统计量:离散度D,用来描述集合中向量之间的离散程度。当搜索得到的校验向量比较完备时,对于原码为卷积码,由于校验向量可以通过移位原码码长依次得到,因此相邻校验向量之间肯定有相同位置的1元素,从任一个校验向量出发向外扩展(即前面的分类过程),最后总能包含所有校验向量,即离散度D=1;对于原码为分组码,由于不同码字间完全独立,校验向量只有属于同一个码字时才会有相同位置的1,因此经过分类之后,离散度等于原码字个数,即D=n/n′。 因此可以通过离散度D的大小来判断编码类型,若D=1,则可认为编码方式为卷积码,否则编码方式为分组码。 本文整体算法包括校验向量搜索、交织存在性识别和编码类型识别,其中校验向量搜索过程计算复杂度较另外两个过程要高得多,因此下面主要针对校验向量搜索过程进行详细分析,设原码字最低码重校验向量数目为y,其他参数具体意义见3.4节。 其次是校验向量精确搜索过程:该过程采用专利[11]中的LDPC译码算法,迭代一次每个校验向量涉及Mtmin次实数域乘法和加法运算,同时调用双曲正切函数tan(·)和反双曲正切函数atan(·)各Mtmin次,由于每次译码前识别得到的校验向量并不完整,所以每次译码运算量小于y个校验向量全部参与译码时的运算量。 通过以上分析,考虑到各种迭代次数,整体算法运算量如下:二进制运算次数为Nc,3·Nc,2·Nc,1·W1+W2次,实数域乘法和加法运算次数少于Nc,3·y·Mtmin次,双曲正切函数tan(·)和反双曲正切函数atan(·)调用次数少于Nc,3·y·Mtmin次。 本节仿真实验以1/2码率卷积码和(15,11)汉明码为例展开测试。其中卷积码生成多项式为g1(x)=1+x+x2+x5,g2(x)=1+x+x3+x4+x6,汉明码生成多项式为G=[1 1 0 0;1 0 1 0;0 1 1 0;1 1 1 0;1 0 0 1;0 1 0 1;1 1 0 1;0 0 1 1;1 0 1 1;0 1 1 1; 1 1 1 1]。利用MATLAB产生5000帧长度为500的卷积码,5100帧长度为510的分组码(汉明码),通过产生1,2,…,500与1,2,…,510的随机排列,分别对卷积码和分组码进行随机交织,后面实验均基于此数据进行。 表1给出了Nc,1=16384,Nc,2=5,p=0.003,t=10时,不同码字选取数目N条件下,卷积码数据粗搜索过程得到的校验向量数目变化情况;表2给出了Nc,1=16384,Nc,2=5,p=0.005,t=10时,不同码字选取数目N条件下,粗搜索过程得到的校验向量数目变化情况。由表1和表2可以看出,码字选取数目N越小,(pwk)N越大,由式(9)可知有更多的校验向量包含于Hsys的行空间,但相同条件下能够搜索出的校验向量数目却不是越来越多,这是因为虽然Hsys的行空间包含有更多有效校验向量,但Hsys的行空间向量数目却越来越多,校验向量的比例在不断变小,要想搜索出更多必须增加迭代次数Nc,1及Nc,2,计算复杂度会越来越高。此外,表1和表2均表明(pwk)N在0.01附近时,能够搜索出更多的校验向量,(pwk)N过小或者过大,在相同计算复杂度情况下,搜索出的校验向量数目均较少,不能对数据进行充分利用,因此需根据(pwk)N的大小进一步确定N的取值。 图2给出了Nc,1=16384,Nc,2=10,t=10,(pwk)N∈[0.005,0.03],误码率p分别为0.003,0.004,0.005条件下,卷积码数据粗搜索过程得到的校验向量数目变化曲线。从图中可以看出,不同误码率下,(pwk)N的最优值一直在变化,随着误码率的降低,(pwk)N的最优值一直在变大;且不同误码率下,(pwk)N即使取最优值,相同迭代次数下搜索出的校验向量数目差异也比较明显,误码率越低,搜索得到的校验向量数目越多,这与前面的分析一致。三种误码率下对应的(pwk)N最优值分别为0.015,0.01,0.005,选取码字数目分别为140,119,109。实际中可以通过计算接收码字的噪声方差σ2,并进一步计算误码率p,通过实验找出该误码率对应的码字选取数目N的最佳值。 图2 校验向量数目变化曲线 表1 p=0.003时不同N的实验结果 表2 p=0.005时不同N的实验结果 图3 归一化平均跨度变化曲线 在搜索得到的最低码重校验向量比例不同条件下,针对卷积码和分组码,β设置为0.4,各进行300次蒙特卡洛仿真实验,得到交织识别正确率的变化曲线如图4。从图中可以看出,分组码和卷积码交织后的归一化平均跨度比较稳定,基本不随校验向量比例的变化而变化;归一化平均跨度的取值始终高于检测门限β且接近理论值0.78,交织存在性的识别率为100%。交织存在性识别效果较理想,主要是因为原始的所有校验向量进行了随机交织,得到的新校验向量无论识别出多大比例,其随机性一直存在,归一化平均跨度值始终跟图3比较接近,而原始校验向量归一化平均跨度值一般较小。由以上可知,对于交织存在性识别,本文提出的校验向量归一化平均跨度效果良好,能够满足实际需求。 图4 交织存在性识别结果 图5 编码类型识别结果 实际中如果能够识别出50%的校验向量,经过LDPC译码之后,码字误码率通常会降低很多,进一步利用前面的算法能够识别出大部分校验向量,则编码类型识别结果不会出现错误。因此无法判断编码类型通常是由于码字误码率过高,识别出校验向量比例过低,即使利用LDPC译码进行迭代也无法进一步降低码字误码率。 本文针对误码情况下采用随机交织码字识别问题,提出了一种容错能力较强的交织及编码类型识别算法。该算法通过码字矩阵变换,小重量向量搜索算法以及LDPC译码进行迭代,能够识别出绝大部分的最低码重校验向量;并进一步提出校验向量的两种统计量,能够对交织的存在性以及编码类型进行有效判断。仿真结果表明,本文算法容错能力较高,能够在误比特率为0.006的条件下,实现交织及编码类型的有效识别,克服了已有方法无法适用于随机交织码字识别的局限性,且本文算法复杂度在可以承受的范围内,能够适用于实际环境。另外,本文算法降低了码字误码率且初步识别出编码结构,能够为进一步交织关系的识别提供明确方向与可靠依据。 [1] 解辉, 王丰华, 黄知涛. 卷积交织器盲识别方法[J]. 电子与信息学报, 2013, 35(8): 1952-1957. Xie Hui, Wang Fenghua, Huang Zhitao. A method for blind recognition of convolutional interleaver[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1952-1957.(in Chinese) [2] Cao S, Chen J, Damask J N, et al. Interleaver technology: comparisons and applications requirements[C]∥Optical Fiber Communication Conference, Atlanta, USA, 2003: 1-9. [3] 解辉, 黄知涛, 王丰华. 信道编码盲识别技术研究发展[J]. 电子学报, 2013, 41(6): 1166-1176. Xie Hui, Huang Zhitao, Wang Fenghua. Research progress of blind recognition of channel coding[J]. Acta Electronica Sinica, 2013, 41(6): 1166-1176. (in Chinese) [4] Sicot G, Houcke S, Barbier J. Blind detection of interleaver parameters[J]. Signal Processing, 2009, 89(4): 450- 462. [5] 甘露,刘宗辉,廖红舒,等. 卷积交织参数的盲估计[J]. 电子学报,2011,39(9): 2173-2177. Gan Lu, Liu Zonghui, Liao Hongshu, et al. Blind estimation of the parameters of convolutional interleaver[J]. Acta Electronica Sinica, 2011, 39(9): 2173-2177. (in Chinese) [6] Cluzeau M, Finiasz M, Tillich J-P. Methods for the Reconstruction of Parallel Turbo Codes[C]∥Proc. IEEE Int. Symposium on Information Theory, Austin, Texas, USA, June 2010: 2008-2012. [7] Jean-Pierre Tillich, Audrey Tixier, Nicolas Sendrier. Recovering the interleaver of an unknown[C]∥Proc. IEEE Int. Symposium on Information Theory, 2014. [8] 刘骏,李静,于沛东. 一种Turbo码随机交织器的迭代估计方法[J]. 通信学报,2015, 36(6): 205-210. Liu Jun, Li Jing, Yu Peidong. Iterative estimation method for random interleaver of Turbo codes[J]. Journal on Communications, 2015, 36(6): 205-210. (in Chinese) [9] 刘骏, 李静, 彭华. 基于校验方程平均符合度Turbo码交织器估计[J]. 电子学报, 2016, 44(5):1213-1218. Liu Jun, Li Jing, Peng Hua. Estimation of Turbo-code interleaver based on average conformity of parity-check Equation[J]. Acta Electronica Sinica, 2016,44(5):1213-1218. (in Chinese) [10] Canteaut A, Chabaud F. A new algorithm for finding minimum weight words in a linear codes: application to primitive narrow-sense BCH codes of length 511[J]. IEEE Transactions on Information Theory, 1998, 44(1): 367-378. [11] Patrick A.Owsley. LDPC Architecture[P]. United States Patent: US7353444, 2005- 05- 06.3.2 校验向量粗搜索
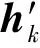
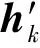

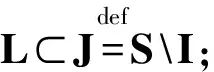
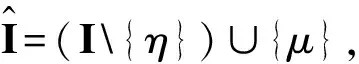
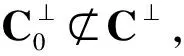
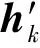

3.3 校验向量精确搜索
3.4 算法总结
4 交织及编码类型识别
4.1 交织存在性识别
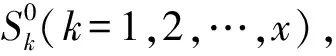
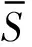
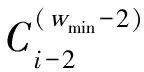
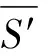
4.2 编码类型识别
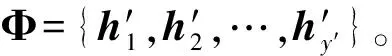
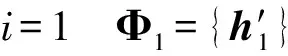
4.3 复杂度分析
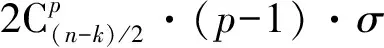
5 仿真实验及分析


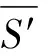
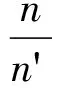
6 结论
