直射通道辅助的北斗弱反射信号捕获算法
2018-08-20周继航杨俊安黄科举
周继航 杨俊安 黄科举 刘 辉
(1. 国防科技大学电子对抗学院,安徽合肥 230037; 2. 安徽省电子制约技术重点实验室,安徽合肥 230037)
1 引言
利用全球导航卫星系统(Global Navigation Satellite System, GNSS)作为辐射源进行海空目标非协同探测具有全球覆盖、信源稳定、隐蔽性强等优势,近年来引起了国内外学者的广泛关注。北斗卫星导航系统简称北斗系统(BeiDou Navigation Satellite System, BDS),是我国自行研制的卫星导航系统,基于安全性、主动性的考虑,将其作为辐射源开展目标探测研究更具有战略意义。BDS与GPS、GLONASS和GALILEO不同,系统包含有 5颗GEO卫星。GEO卫星为同步轨道静止卫星,可避免由于卫星相对地面高速运动而带来的自身多普勒频移影响,在信号捕获时比其他卫星辐射源更加简单快捷。由于其轨道的固定性,信号捕获理论上可以获得更长的积累时间,以提高微弱反射信号的信噪比。此外,北斗GEO卫星轨道位置均在亚太区域,是对我国近海进行目标非协同探测的一种非常理想的辐射源。本文研究背景是以北斗GEO卫星作为辐射源,接收平台为地球低轨道卫星(LEO)的海面目标反射信号的处理问题。
基于地球低轨道卫星的探测接收平台相较于机载平台轨道高度较高、运行速度快,在相同的视角下能够检测更大区域,并且能实现对多个海域的快速扫描。LEO平台因处于高动态和高轨道的条件下,海面目标反射到达接收前端的信号非常微弱。与直射信号相比,反射信号由于路径损耗造成信号强度更为微弱。北斗信号到达地面的最低功率为-133 dBm,反射后到达低轨道星载接收机射频前端时的信号功率仅有-180 dBm~-150 dBm左右[1],常规的信号捕获算法难以捕获如此低功率的信号。本文针对以上问题提出了利用直射通道信号辅助反射信号捕获的算法,该算法在短时匹配滤波器-快速傅里叶变换和简化差分相干累积的基础上,加入了从直射信号中提取到的先验信息,来辅助微弱反射信号的捕获,能够进一步提高捕获灵敏度。
2 非协同探测信号模型
北斗卫星发射信号的电磁波为右旋极化信号(RHCP),右旋极化信号经海面和目标反射后,其极性会发生反转,在卫星高度角大于6.8°时,变为以左旋极化信号(LHCP)为主要分量[2]。考虑到北斗信号的这种特性,星载接收机采用双天线双通道设计,RHCP天线向上对准北斗卫星接收直射信号,LHCP天线向下对准探测区域接收目标反射信号,图1为接收机结构示意图。

图1 星载接收机结构示意图
2.1 直射通道信号建模
星载接收机直达波通道所接收到的信号可表示为:
sD(t)=ARF(t)D[t-τ(t)]C[t-τ(t)]
cos[φ(t)]+nRF(t)
(1)
式中:ARF(t)表示接收到北斗卫星的RF信号幅度电平;D[•]表示当前北斗卫星的导航电文数据码信号;C[•]表示该北斗卫星的C码信号;φ(t)表示接收到的载波相位;τ(t)表示调制在B1载波上的C码信号从卫星天线相位中心发射后到达接收机天线相位中心的路径传播延迟,即码相位的空间传播延迟;nRF(t)表示双边功率谱密度为N0/2的AWGN噪声。
由于北斗信号可近似看作准单色的相位调制球面波信号,故接收点R处的直射信号的场强可以表示为[3]:
(2)
(3)
式中A表示幅度因子;式(4)和(5)中,Rd表示北斗卫星T到接收机R的距离;c代表光速;a(t)是北斗调制信号;k=2πfL/c表示接收机和卫星间的载波数;fL为北斗载波频率,即1561.098 MHz;PtGt为北斗卫星有效全向辐射功率EIRP=34.1 dBW;Gr为接收天线增益;λ为载波波长;Lf为大气损耗,系统几何结构图如图2所示。

图2 几何结构示意图
现今地基北斗接收机技术已相对成熟,本文的星载接收机位于太空中,直射信号的信道环境较好,信号的处理和导航信息的提取相对于地面要简单的多,这里对于直射信号信息提取过程不再赘述。从直射信号导航信息中解析出的载波多普勒频移、码相位、精准同步时间、历数与星历等信息辅助反射通道信号的处理。
2.2 反射通道信号建模
反射信号与直射信号的信号形式相似,仅是时延和码相位的不同,场强表达形式可以直接从直达信号形式推导而来[3],具体推导过程不再赘述,反射信号的几何结构如图2所示,在接收机R处收到的目标反射点信号场强为:
(4)

通过对直达信号和反射信号的模型分析,建立了信号场与空间的关系,为下一步进行性能分析做好准备。
3 反射信号捕获算法
3.1 本地辅助载波和本地辅助码产生
反射信号载波频率产生和伪随机码相位的产生是以直射信号的时间延迟和多普勒频移为基准的。生成多频载波比较常用的方法是直接数字频率合成技术(Direct Digital Synthesis,DDS),如图3所示,通过参考直射信号的载波频率,将反射信道的本地载波基准频率与其同步,FCWR(fE)为频率控制字,调整直射信号与反射信号镜面分量间的多普勒频率差,FCWR(ΔfD)调整反射信号多普勒频率分辨率。相较无直射信号辅助而言,有直射信号辅助时将大大减少频域搜索时间,提高反射信号的捕获速度。
在辅助本地码产生上利用一组由移位寄存器组成的延迟线来生成延迟伪随机码,如图4所示。首先将反射通道的基准码与直射通道某个起始码相位对齐,然后以fRs=L·fs的频率对其进行重采样产生的新码序列通过长度为Ndelay的移位寄存器,单个移位寄存器产生的时间延迟为1/(L·fs),对移位寄存器输出的码序列进行重采样即可形成分辨率可调的本地多延迟伪随机码序列,将此序列传送给反射通道作为其本地基准伪码。
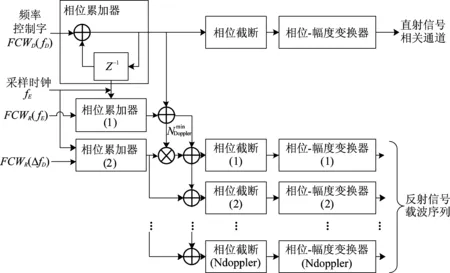
图3 有辅助的反射通道本地载波生成方法

图4 有辅助的反射通道本地码生成方法
3.2 直射通道辅助算法
常用的多周期捕获的方法是延长积分时间的相干累积和非相干累积法。导航信号的特殊性导致相干累积的时间有限,非相干累积法又存在着“平方损耗”,使得它们在信号捕获的实际应用中都存在一定的缺陷[4]。差分相干累积和非相干累积的不同之处在于:在非相干累积中,来自相同采样点的噪声被平方相加,造成了“平方损耗”;而在差分相干累积中,来自相邻采样点的噪声被共轭相乘,一次差分累积可以减少“平方损耗”,在提升信噪比方面要强于非相干累积法[5]。相关文献提出了短时匹配滤波器(Short-Term Matched Filtering,STMF)与FFT结合的方法(STMF-FFT),该方法的核心思想是在搜索码相位的同时就能得到多普勒频移值,从而将相位、多普勒频移的二维搜索问题变成相位的一维搜索问题[6],大大减少了捕获时间,这对于反射信号的处理有借鉴意义。本文将直射通道辅助信息加入到STMF-FFT和简化差分相干积累(Simplified Differentially Coherent Integration, SDCI)算法中,在缩短搜索时间的同时提高信噪比,提高接收机灵敏度,其算法结构示意图如图5所示。
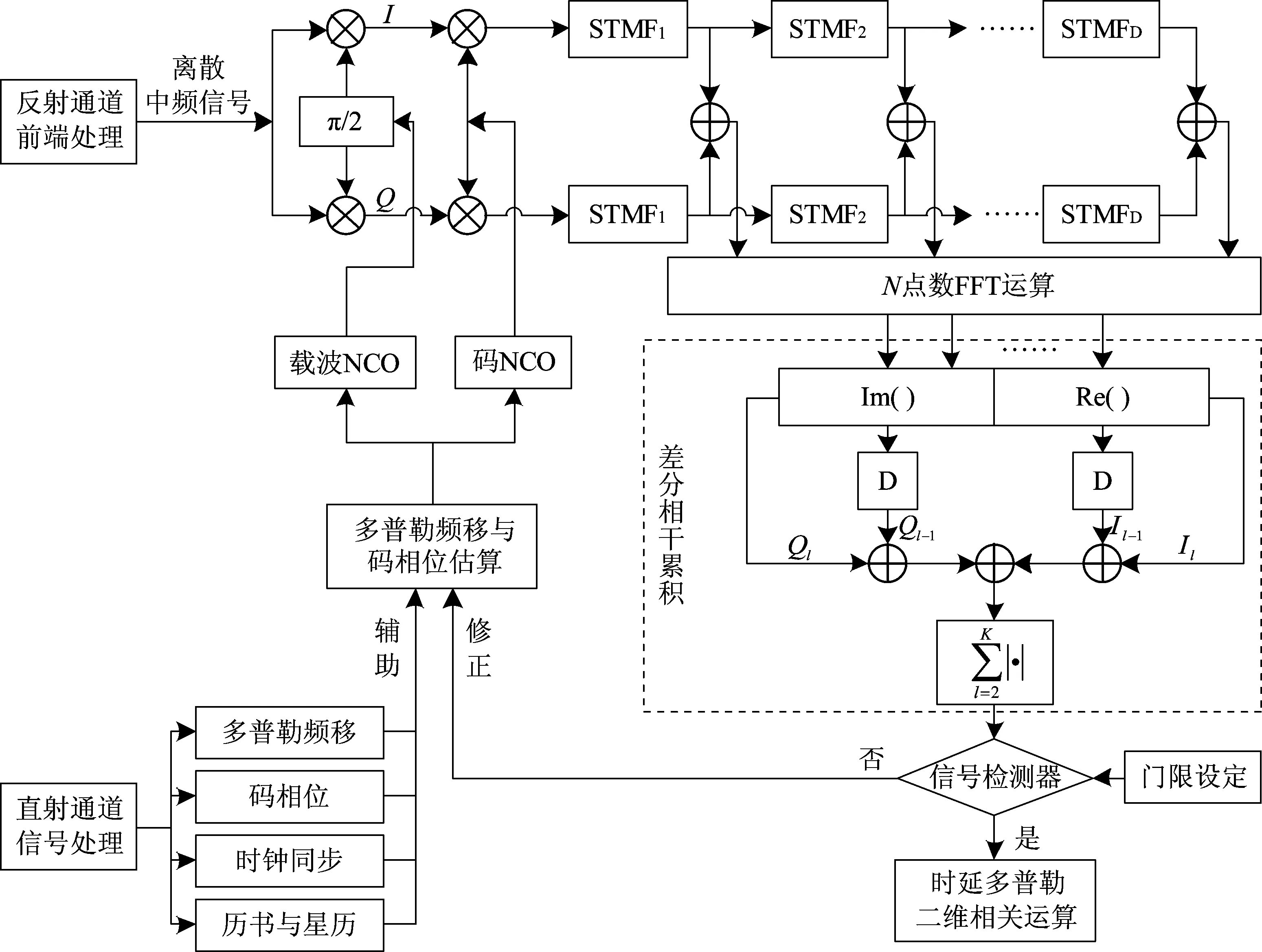
图5 反射信号捕获算法示意图
北斗反射信号经过接收机射频前端下变频、滤波、放大后经过周期为Ts=1/fs的A/D采样变为离散中频信号si(n)表示为
si(n)=A·Di(nTs-Td)·Ci(nTs-Td)×
cos[(ωIF+ωd)nTs+φ]+e(nTs)
(5)
式中:A为反射信号幅值;Di(nTs-Td)为第i颗北斗卫星的导航数据码;Td为反射信号相对于北斗卫星发射信号的时间延迟;Ci(nTs-Td)为第i颗卫星的伪随机码;ωIF为中频角频率;ωd为多普勒频移角频率;φ为反射信号载波初始相位;e(nTs)表示高斯白噪声。
反射通道的本地载波NCO和码NCO需要以直射信号捕获中的本地信号作为参考,具体产生方法在2.1节已经说明。离散中频信号与载波进行混频,忽略高频分量后信号表示为复数形式zi(n)
zi(n)=A·Di(nTs-Td)·Ci(nTs-Td)×
exp[j(ωdnTs+Δφ)]+e(nTs)
(6)
式中:Δφ为反射信号与辅助载波信号的相位差。将全部预检测相关积分时间T划分为D段,每段积分时间为Tp,则T=Tp×D。在总的相关积分时间T内,参与积分的点数为L=M×D,M为单个短时积分时间内的点数,则Tp=Ts×M。

k=0,…,D-1
(7)

当辅助伪随机码与反射信号的伪随机码对齐后,在短时积分时间内的数据码保持不变,则归一化输出可表示为
exp{j[ωdTs(kM-M/2-1/2)+Δφ]}
k=0,…,D-1
(8)
将D个短时STMF的输出补N-D个零,进行N(N≥D)点的复数FFT运算,FFT的第i(i=0,1,…,N-1)个点的输出归一化幅值|X(i)|为
(9)
依据预先设置的门限值,当输出的|X(i)|为最大幅值,即πfdTsM=πi/N时,该幅值超出设置门限,则说明反射信号伪码已经与辅助本地伪码对齐[7]。此时记录超出门限时的位置i,然后将输出的幅值进行重新排列使其能够与连续信号的频谱相互对应,即推算出多普勒频移的粗估值fd
(10)
反射信号在经过STMF-FFT后进行差分相干累积,本文利用改进的简化差分相干累积法(SDCI)对信号弱进行检测,其核心思想是减小信号累积过程中的平方损耗,利用两个相邻历元相关值的非相关性,对两个相邻历元的相关值进行点积相乘[8],对于检测量EDCI的定义为
(11)
式中:K为差分相干累积(DCI)的次数;l表示第l次STMF-FFT信号处理的结果。
通过DCI处理获得了比传统非相干累积更高的信噪比,但由于单次处理都要经过平方与开方运算,DCI处理过程的运算量比较大,对硬件要求较高,在星载条件下载荷有限的情况下难以适用,需要对DCI方法进行简化,首先将检测量由幅度包络替换为能量包络,即
(12)
信号经过相关积分,I路中仅有信号存在,Q路中仅有均值为零的噪声存在,由此可知
(QlIl-1-IlQl-1)2≈0
(13)
此时SDCI的检测量E可以表示为
(14)
通过与设置的门限值比较决定是否捕获到反射信号。
3.3 捕获灵敏度与时间
定义事件H1为反射信号存在,事件H0为反射信号不存在,分别对应的概率密度函数为f(E|H1)和f(E|H0)。在H1条件下,检测概率Pd是自由度为2(K-1)、非中心参数λ=(K-1)·2A2的非中心χ2分布和自由度为2(K-1)的中心χ2分布概率密度函数之和的积分运算[12]。
式(14)定义了SDCI的检测量,在H0条件下,设定判决门限为F,虚警概率Pfa表示为
(15)
式中:Kn(·)表示第二类n阶修正贝塞尔函数;Γ(·)表示伽马函数。

(16)
式中
β(τ)=(A0·R(τ))2/(2σn)2
sinc(x)=sinx/x
(17)
信号差分相干处理后信噪比
(18)
相关文献[10-11]对于其他的参数设置做了详细的介绍,这里不再赘述,这里重点考虑A0对相干处理信噪比的影响。从式(17)、(18)中可看出,输出信噪比随参数A0的减小而提高,A0与多普勒频移搜索区间大小Δfd有关。有直射信号的载波频移信息辅助时,搜索多普勒频移点与真实多普勒频偏接近,即Δfd较小,信噪比变大,即在有直射通道的信号多普勒频偏作参考对反射信号进行处理时,可以获得更高的信噪比。
本文的信号捕获时间定义为搜索并捕获到北斗反射信号所需的时间。由于信号捕获时间是一个随机变量,通常使用平均捕获时间Ta来表示
(19)

(20)
其中
(21)
(22)

根据图2的几何关系,可根据星历及轨道参数精确获得发射机与接收机的位置以及直射通道码相位φd,则反射通道码相位的起始搜索位置为
(23)
4 仿真分析
本文利用仿真北斗B1频段信号对捕获算法展开实验分析,使用仿真信号便于可控的设置接收信号的伪随机码相位偏移量、多普勒频移量以及信噪比等具体参数,能够避免非相关因素对捕获算法分析的影响。直射通道信号作为已知信号使用,对直射信号进行时延和多普勒频偏处理并加入噪声模拟接收到的反射信号。对于本文的研究背景而言,反射信号的导航电文不是本文研究的重点,这里使用与北斗导航电文速率一致的50 bps的随机码替代。具体参数设置为:带宽为4.092 MHz,采样频率为5 MHz,随机设置多普勒频移值和码相位延迟值,根据接收机的实际噪声基底,设置噪声强度为-110 dBm,检测概率为0.95,虚警概率为10-6,STMF-FFT中,受制于硬件条件,预检测相关积分时间不能划分过多,本次实验按照图5的信号处理流程,划分为32段,短时相关后做64点FFT,进行3次SDCI运算。模拟不同信号强度下分别比较有直射通道辅助的SDCI和无直射通道辅助的SDCI的捕获效果。
反射后到达低轨道星载接收机射频前端时的信号功率当信号强度为-150 dBm,即信噪比为-40 dB时,反射通道采用有直射通道辅助的SDCI算法在多普勒频率、码相位一维的捕获效果和多普勒-码相位二维捕获效果如图6所示,此次实验的多普勒频移值为40 Hz,码相位延迟为2200 chips,可以看出在此信噪比条件下,相关值出现显著峰值,能够准确捕获出信号。

图6 有直射通道辅助的SDCI算法捕获图
在相同实验条件下,采用无直射通道辅助的SDCI算法的捕获效果如图7所示,可以看出在此信噪比条件下,噪声对捕获峰值的干扰大,信号的相关峰值已经淹没在噪声中,导致虚警概率增大,无法准确捕获出信号。

图7 无直射通道辅助的SDCI算法捕获图
为定量分析直射通道辅助对于反射通道的影响,在不同信噪比条件下采用有辅助的SDCI算法进行100次试验得出平均捕获时间,变换二维搜索空间大小即不同q值,仿真得出反射信号捕获时间与信噪比之间的关系如图8所示。q值由二维搜索空间决定,但实际情况下搜索空间总存在不确定性,不可能等于0,而受制于接收机相关器个数,平均捕获时间存在着理论极值,这与具体硬件条件有关。仿真结果可以看出,同等信噪比条件下当搜索空间越小即直射通道辅助程度越高所需的捕获时间也越短,证明了直射通道辅助的有效性。
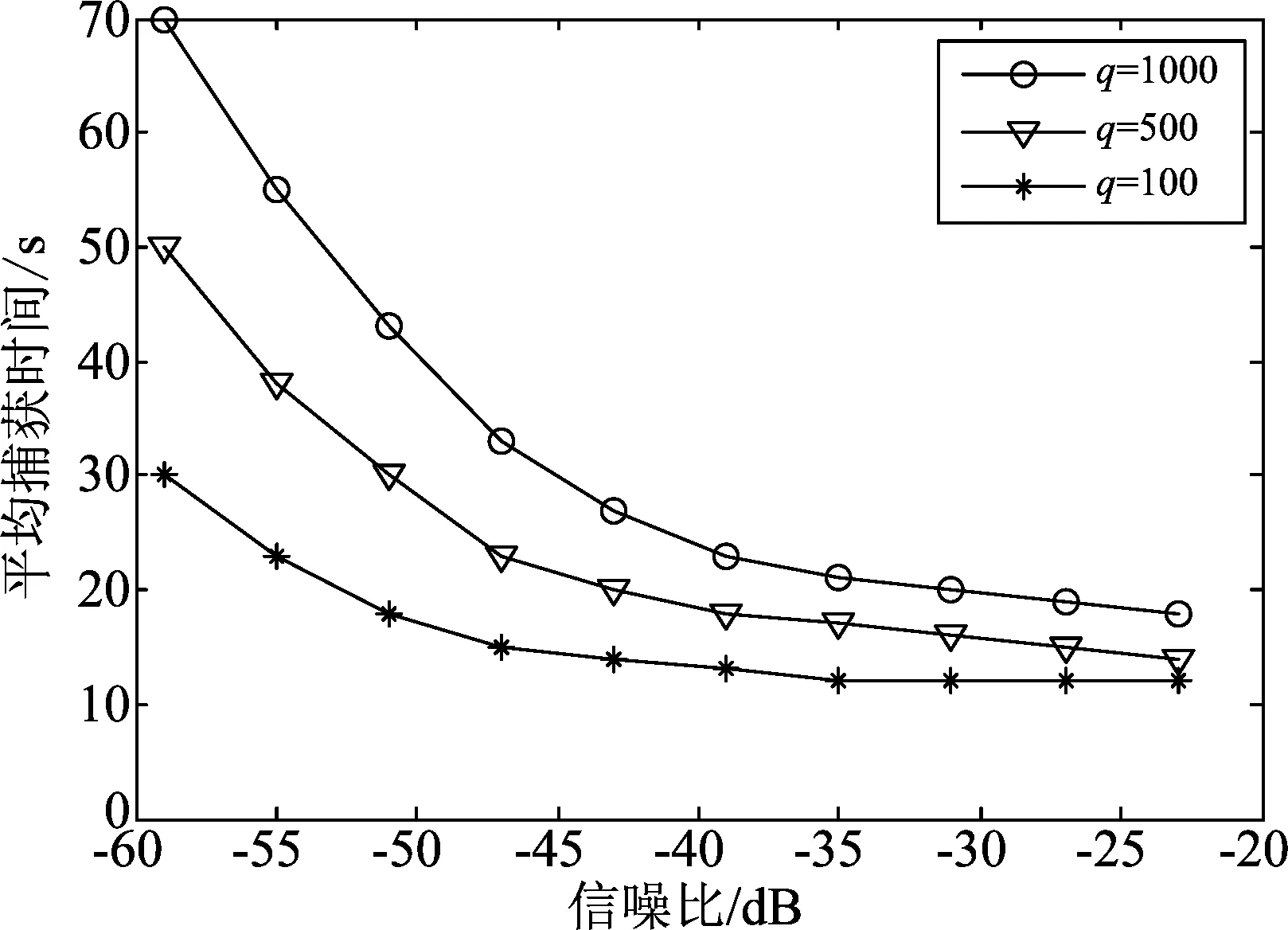
图8 不同q值条件下捕获时间与信噪比之间的关系
为了做对比,本文在-60~-30 dB的信噪比条件下,分别采用有辅助的SDCI、无辅助的SDCI和传统非相干累积信号捕获算法计算检测概率,效果如图9所示。从实验结果可以看出,在检测概率为0.95时,有辅助的SDCI算法可以在信噪比为-41.3 dB的条件下捕获信号,灵敏度可达到-151.3 dB;而无辅助的SDCI和传统非相干累积算法灵敏度仅能达到-148.2 dBm和-139.8 dB,相较后两种方法,有辅助的SDCI算法能够提高灵敏度3.1 dB和11.5 dB。

图9 三种算法不同信噪比下的检测概率
在信号捕获时间上,由于量化时间跟具体硬件性能有关,这里根据前文理论推导,仅就本实验条件下的平均捕获时间进行实验。在-40 dB信噪比的条件下,有辅助的SDCI算法十次平均捕获时间为19.5 s;而无辅助下的SDCI算法十次平均捕获时间为59 s。由于在有直射信号辅助的条件下星历参数已知,而且多普勒频移和码相位搜索范围能控制在很小的范围内,与文献[8]相比,捕获时间大大缩短,实验验证了前文的理论分析。

表1 三种算法的灵敏度与捕获时间比较
5 结论
本文在STMF-FFT和简化差分累积算法基础上加入了直射通道辅助,对反射信号的捕获算法展开了研究,通过实验验证了在有辅助时,捕获灵敏度和捕获时间均能有所提高,相较无辅助SDCI,灵敏度提高3.1 dB,能够捕获强度低至-151.3 dBm的弱反射信号,平均捕获时间缩短39.5 s,已经满足反射通道的要求。这在一定程度上解决了利用北斗卫星信号进行海面目标探测的微弱反射信号捕获问题。
[1] 马小东, 张凤元, 杨东凯,等. 星载GNSS海面散射信号功率分析与接收方法研究[J]. 计算机工程与应用, 2012,48(S2):199-202.
Ma X D, Zhang F Y, Yang D K.Power analysis and reeeiving method study of GNSS sea surface seattering signal for space-borne[J].Computer Engineering and Aplieations,2012,48(S2):199-202.(in Chinese)
[2] 邹文博, 张波, 洪学宝,等. 利用北斗GEO卫星反射信号反演土壤湿度[J]. 测绘学报, 2016, 45(2):199-204.
Zou W B, Zhang B,Hong X B, et al.Soil moisture retrieval using reflected signals of BeiDou GEO satellites[J].Acta Geodaeticaet Cartographica Sinica, 2016, 45(2): 199-204. (in Chinese)
[3] Garrison J L. A Statistical Model and Simulator for Ocean-Reflected GNSS Signals[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(10):1-13.
[4] Lin S, Chen L. Inter-block Differentially Coherent Integration for GPS L5 signal acquisition[C]∥IEEE Third International Conference on Information Science and Technology. IEEE, 2013:1217-1220.
[5] 李新山, 郭伟. 基于平均相关和差分相干累积的微弱GPS C/A码信号精密捕获算法[J]. 通信学报, 2015, 36(5):112-119.
Li X S,Guo W.Fine C/A code acquisition algorithm for on averaging correlation and differential weak GPS signal based coherent accumulation[J]. Journal on Communications,2015, 36(5):112-119. (in Chinese)
[6] Pan Y, Zhang T, Zhang G, et al. Analysis of an improved acquisition method for high-dynamic BOC signal[J]. Journal of Systems Engineering & Electronics, 2016, 27(6):1158-1167.
[7] 王娜子, 鲍李峰, 高凡. 逐历元GNSS-R测高单差和双差算法[J]. 测绘学报, 2016, 45(7):795- 802.
Wang N Z,Bao L F,Gao F.Inproved water level retrieval from epoch-by-epoch single and double difference GNSS-R algorithems[J].Acta Geodaeticaet Cartographica Sinica, 2016, 45(7):795- 802. (in Chinese)
[8] An Y, Cai B, Ning B, et al. BeiDou B1 signals fine acquisition algorithm based on simplified differentially coherent integration[J]. Journal of Beijing Jiaotong University, 2014, 38(2):1-7.
[9] 陈坡. GNSS/INS深组合导航理论与方法研究[D]. 郑州:解放军信息工程大学, 2013.
Chen P. Research on Theories and methods of deeply coupled GNSS/INS integrated navigation[D]. Zhengzhou:PLA Information Engineering University,2013. (in Chinese)
[10] 吴迪军, 徐振海, 张亮. 极化空时自适应匹配滤波检测器[J]. 电子学报, 2013, 41(4):744-750.
Wu D J,Xu Z H,Zhang L.Polarization-space-time adaptive matched filter detector[J]. Acta Electronica Sinica, 2013, 41(4):744-750. (in Chinese)
[11] Esteves P, Sahmoudi M, Boucheret M L. Sensitivity characterization of differential detectors for acquisition of weak GNSS signals[J]. IEEE Transactions on Aerospace & Electronic Systems, 2016, 52(1):20-37.
[12] Gowdayyanadoddi N S, Broumandan A, Lachapelle G, et al. Indoor GPS positioning using a slowly moving antenna and long coherent integration[C]∥International Conference on Localization and Gnss. IEEE, 2015:1- 6.
