多线切割机主轴振动模态分析

2018-08-17谢耿勋

电子工业专用设备 2018年4期

李欢，谢耿勋，郝禄，唐强

(中国电子科技集团公司第四十五研究所，北京 100176)

近年来，为了提高设备的工作效率，设计人员在不断地提高主轴的转速。然而，当主轴达到一定转速时，设备就会产生振动，导致零件的损坏，严重时还会发生事故。目前，主轴的振动问题[1，2]越来越引起设计人员的关注，而且已经成为了评价一台设备质量的重要标准。为此，本文采用有限元模拟的方式主要针对设备主轴进行振动模态分析，求出其临界转速，避免主轴在高速旋转时产生振动，防止对设备造成损伤。尤其对于金刚石线多线切割机而言，主轴的振动问题尤为重要。因此，本文主要以金刚石线多线切割机为研究对象，建立其主轴系统的有限元模型，对多线切割机主轴进行振动模态分析[3]，计算出其临界转速。

目前，振动模态分析已经成为研究结构动力学特性的一种重要的方法[4]，在工程振动领域中有着极其广泛的应用。通过对设备进行模态分析，可以清楚地知道设备的结构在易受影响的频率范围内的每一阶模态的主要特性，从而便可以推断出此结构在这些频率受到内部或者外部何种激励作用下产生的实际响应，有效地避免了因共振所产生的结构损伤和破坏[5]。

1 振动模态分析理论

振动模态分析理论有三个基本假设。一是线性假设，即结构的动态特性是线性的，它的动力学特性可用线性微分方程来进行阐述。二是时不变性假设，即结构的动态特性与时间无关，因此微分方程的系数是和时间无关的常数。三是可观测性假设，即系统动态特性所需要的数据都是可监控的。下面给出了系统的结构动力方程[6]：

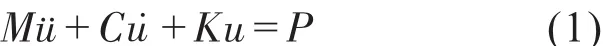
式中：M—系统的质量矩阵；C—阻尼矩阵；K—刚度矩阵；P—系统承受的外界载荷之和；ü-系统加速度矢量；u·—系统速度矢量；u—系统位移矢量。

而对于无阻尼的系统，即动力方程中的C=0，P=0。将其带入式(1)得：

然而对于一个线性系统，无阻尼振动的形式为以下公式：

将方程(3)带入到方程(2)中，得出：

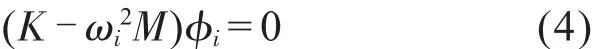
但是方程(4)必须存在非零解，也就是说φi不为0，则K-ωi2M的行列式必须为0才能满足条件，即：

2 有限元模型建立

本文以中国电子科技集团公司第四十五研究所研制的金刚石线多线切割机主轴前后轴为研究对象建立有限元模型。由于要计算主轴的临界转速，因此只选取其旋转部位为主要研究对象，即前后轴轴芯和轴辊，示意图如图1所示。

图1 数值模型

中国电子科技集团公司第四十五研究所研制的金刚石线多线切割机主轴前后轴以及轴辊的材料均为20Cr，其弹性模量为 206 GPa，密度为7.82 g/cm3，泊松比取0.3。为了便于进行有限元分析，提高网格划分质量和计算速度以此来提高计算结果的精度，我们在建模的过程中忽略模型中的一些小特征，例如倒角、螺纹等细小部分，从而对多线切割机主轴系统进行适当的简化[7]。本文采用实体单元进行有限元计算，网格采用四面体网格进行划分。根据实际工况，前后轴芯与轴辊均采用绑定约束，同时释放其前后轴的周向位移，即只允许主轴绕中心转动而不允许其发生平动，其有限元模型如图2所示。

图2 有限元模型

3 振动模态计算结果分析

本文采用Lanzos法对主轴进行模态分析。由于低阶模态对主轴整个系统影响较大，因此，计算出主轴的前5阶模态，并得到其阵型，如表1所示。

表1清楚地反映了金刚石线多线切割机主轴的前5阶模态的频率以及主轴系统6个自由度重要的阵型参与系数。其中阵型参与系数数值的绝对值表示该阵型在这个自由度方向的强弱，表中黑体字部分为绝对值数值最大的部分，说明该阵型主要以此自由度方向为主。因此由表1我们可以得出，主轴系统的前5阶模态的阵型均为旋转阵型，继而得出主轴系统的阵型主要以旋转阵型[8]为主，即主轴只有在旋转时才容易产生振动。

同时也能够清楚地反映出金刚石线多线切割机主轴系统的一阶模态为1.28 Hz，即主轴系统的固有频率为1.28 Hz。同时也能看出主轴系统的2～5阶模态的频率分别为 210.5 Hz，218.3 Hz，405.9 Hz，413.6 Hz。其中2阶模态和3阶模态、第4阶模态和第5阶模态的频率在数值上较为接近，这是由于模型的对称性产生的对称模态。

表1 前5阶模态阵型

主轴的转速和频率的关系为：

其中：n为转速，f为频率，将主轴系统的频率转化成临界转速，如表2所示。

由表2可知，该金刚石线多线切割机在转速达到76.8 r/min和12 630 r/min时会产生振动现象。然而工作时最高的转速为3 274 r/min。所以，主轴在刚启动时较易产生振动，因此我们应避开其一阶频率，快速的提高主轴的转速。由于篇幅的原因，以下给出了主轴系统的前三阶模态[10]，如图3、图 4、图 5 所示。