非对称半桥LLC谐振变换器同步整流数字设计
2018-08-17杜建华
洪 良 ,杜建华 ,王 均 ,马 皓
(1.浙江大学电气工程学院,杭州 310027;2.北京控制工程研究所,北京 100190)
近年来,在电力电子领域中,高功率密度和高效率的开关电源越来越受人们的欢迎。由于能够实现原边开关管的零电压开通和副边整流管的零电流关断,LLC变换器得到了越来越广泛的运用[1-18]。在低压大电流的运用场合,为了减小副边整流管的导通损耗从而提高LLC变换器的整机效率,同步整流技术代替不控整流得到运用。如何产生最适的同步整流驱动是同步整流技术的核心关键。同步整流技术是LLC谐振变换器的热点问题之一,目前主流的策略分为两类方法,一类直接法,一类间接法,间接法中存在多种信号的识别方式。文献[1]中提出用通过同步整流管的电流产生来产生同步整流驱动。这种产生驱动的方法简单易行,但是要求额外的添加电流互感器和相应的外围控制电路;文献[2]中提出通过检测同步整流管两端的DS电压来产生同步整流驱动。这种方法依赖于同步整流管的寄生参数;文献[3]中提出通过开环外设同步整流管的导通时间来产生同步整流驱动。这种方法是一种比较粗略的控制方法,没有达到效率的最优;文献[4-6]中提出仅仅通过检测输出电压来和自适应的同步整流时间的调整产生同步整流驱动,这种方法适用于低压输出,而且对于AD芯片或者AD模块的分辨率要求比较高,在动态性能要求比较高的场合适用。
本文主要针对非对称半桥LLC谐振变换器的同步整流技术数字控制方式进行分析,提出了基于原边谐振电流和输出电压控制副边同步整流管导通时间的控制策略,有利于效率的提升。最后通过搭建一个基于FPGA的300 W的实验样机进行方案的验证,实现了整机效率92.1%。实验结果与一种传统的同步整流的实验结果对比,满载工况下整机效率提高了0.5%。因此这种控制方法具有一定的工程实践意义。
1 非对称半桥LLC谐振电路工作过程分析
非对称结构LLC谐振型变换器如图1所示,副边电路折合到原边等效电路如图2所示,相应的谐振电流波形和驱动波形如图3所示。图中,谐振电容为Cr,谐振电感为Lr,励磁电感为 Lm,原边 MOS管分别为SM1、SM2,副边同步整流管分别为SR1、SR2,输入电压为 Vin,输出电压为 Vo1,负载为 Ro1。本文主要讨论欠谐振模式下的同步整流控制策略[8-9]。
模态 1(t0<t<t1):当 t=t0时,SM1零电压开通,A、B两点间的电压VAB等于Vin,Cr与Lr参与谐振,谐振电流ir大于励磁电流im。此时副边电流大于0,此时理应开通同步整流管SR2和SR4。此模态中,im(t)、iL(t)、VCr(t)的表达式分别为
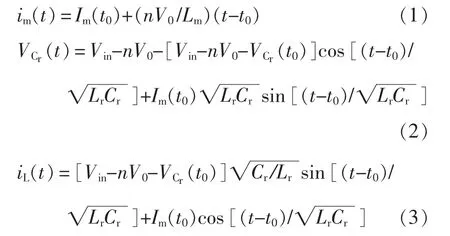
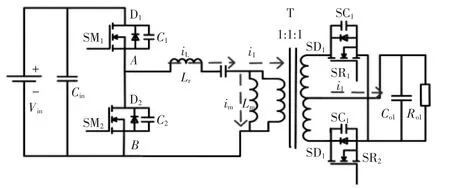
图1 非对称结构LLC谐振型变换器Fig.1 LLC resonant converter with an asymmetrical structure

图2 非对称结构LLC谐振型变换器等效电路Fig.2 Equivalent circuit of LLC resonant converter with an asymmetrical structure
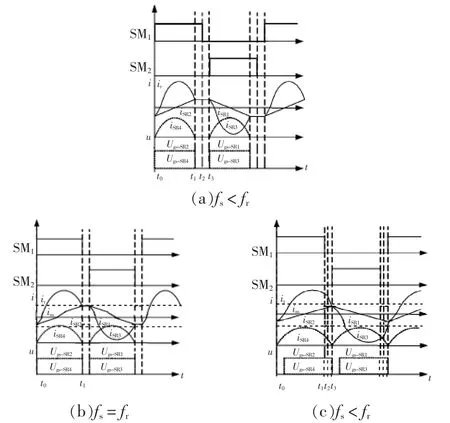
图3 LLC谐振变换器的典型波形Fig.3 Typical waveforms of LLC resonant converter
模态 2(t1<t< t2):当 t=t1时,谐振电流 ir等于励磁电流im,此时副边电流等于0,此模态理应关断同步整流管。此模态中,im(t)、iL(t)、VCr(t)分别表示为
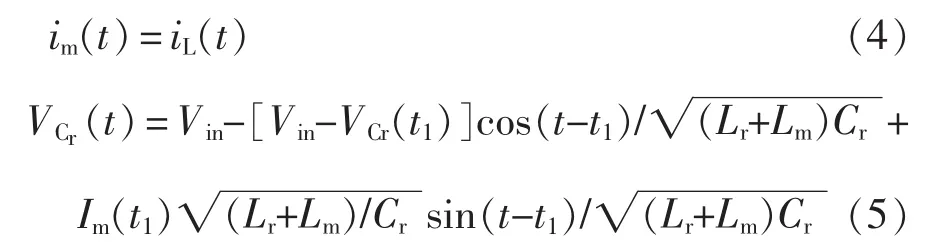
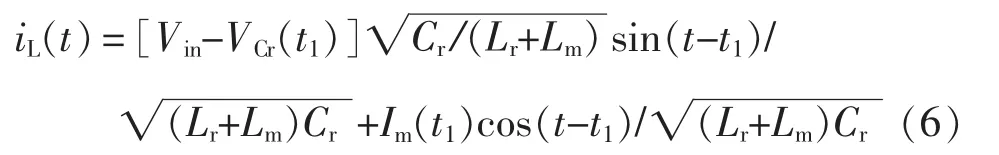
模态 3(t2<t<t3):当 t=t2时,SM1关断,ir等于 im,此时副边电流仍等于0,此模态理应关断同步整流管。由波形可以得出,在完全谐振时,副边整流驱动可以跟原边主开关管同步。在过谐振状态下,由于副边整流电流被强制拉低为0,所以理论上副边整流的驱动应该滞后于相应的原边开关管的驱动。但是由于死区时间较短,最小的死区时间是结电容完成充放电的时间。如果外部有干扰或者导致主开关管导通时,其对应的另外一个同步整流管仍处于导通状态,此时变压器将会短路,这是工程实际中所不希望的。从安全角度考虑,在过谐振状况下,同步整流管的驱动可以与主管驱动完全同步。最后,为计算方便,不考虑死区时间,有

2 谐振过程的时域分析
图2是多路输出LLC谐振变换器的等效电路,方程组式(1)~式(7)做标幺化处理。
参数定义如下:电压基准Vbase=nV0;电流基准Ibase=V0/nR0;电压增益基准 M=nV0/Vin;频率基准;角频率基准。
分析过程用相角代替时间,因此可得
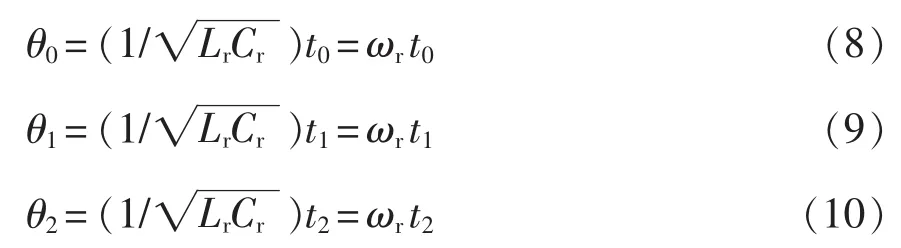
在欠谐振工况下,由电压电流的波形可以得到一些前提条件,即
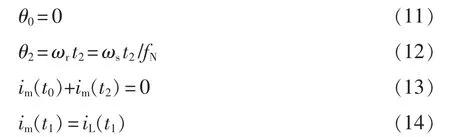
根据方程式(7)~式(13),可以得到以下方程。
(1)当 t0<t<t1时,有
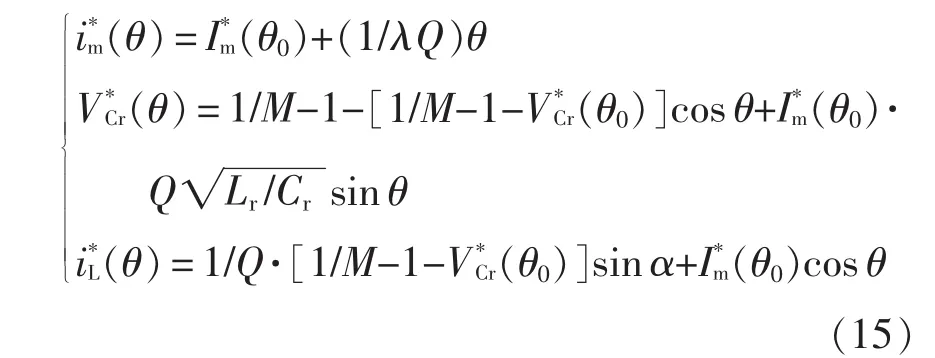
(2)当 t1<t<t2时,有
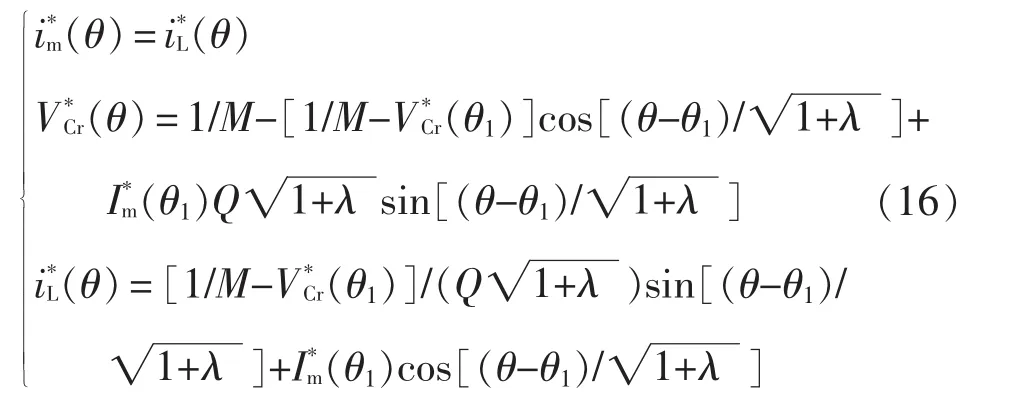
由以上分析可得,输出的平均电流满足下列方程
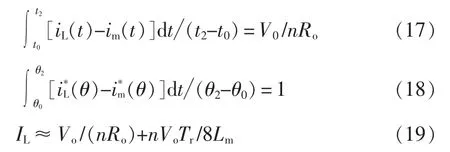
半桥结构中谐振电容充当了隔直电容的作用,因此隔直电容上的电压满足以下方程
LLC谐振变换器,变频控制下,上下管驱动的占空比均为0.5,因此需要满足

本文设计LLC谐振电路参数如表1所示。输入电压范围为95~105 V,输出电压为25 V,在轻载或者空载状况下,考虑到MOS同步整流管的驱动损耗,因此关断同步整流管。只有在负载大于一定值的时候才启用同步整流。综合方程式(11)~式(21),可以得到隐函数 f(θ1,fN,Q,λ)=0,从隐函数可以得到Q、λ与 fN三者都可以影响同步整流管的导通时间。由于不能得出关于同步整流管的导通时间的显函数表达式 θ1→φ(fN,Q,λ),基于 Maple.18,隐函数图像分别如图4和图5所示。
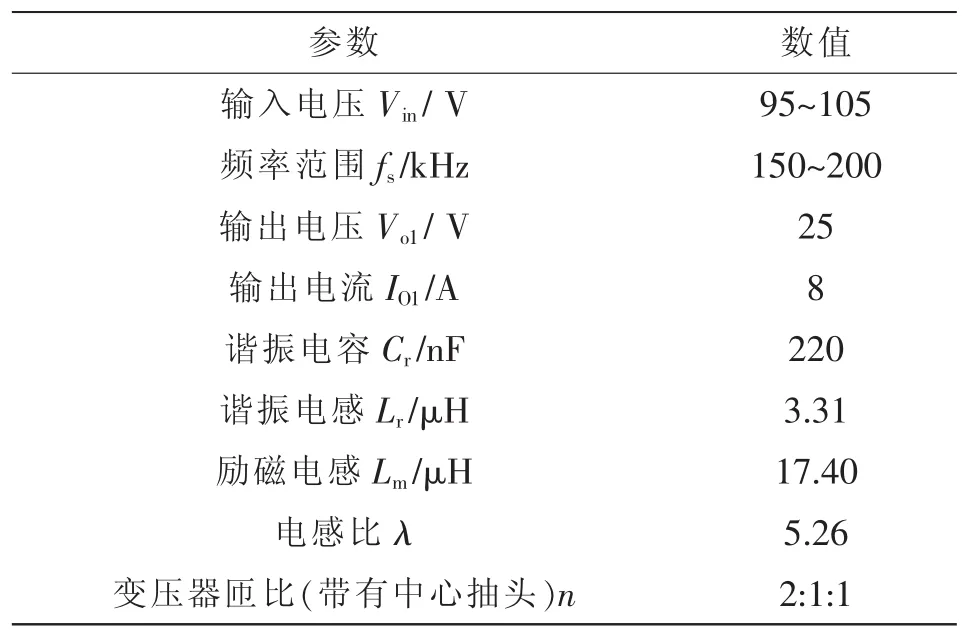
表1 LLC谐振变换器参数Tab.1 Parameters of LLC resonant converter
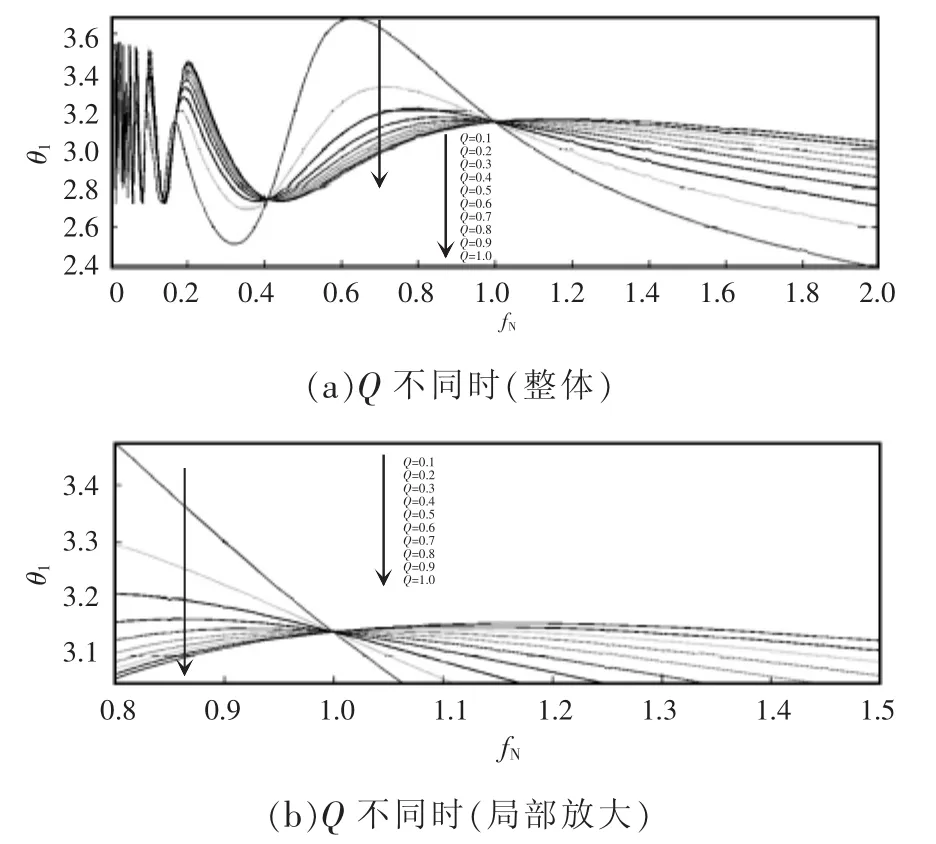
图4 品质因素Q对同步整流管导通时间的影响Fig.4 Influence of Q on the conduction time of synchronous rectifiers

图5 电感比λ对同步整流管导通时间的影响Fig.5 Influence of λ on the conduction time of synchronous rectifier
3 LLC同步整流数字设计
当电感比λ一定时,品质因素对同步整流管的导通时间的影响如图4所示。当品质因素一定时,电感比λ对同步整流管的影响如图5所示。当λ>5,归一化频率 fN在 0.83~1.0 之间时,从图3(b)中可得电感比λ的影响很小可以忽略不计。因此主要考虑品质因素对同步整流导通时间的影响。当品质因素固定,归一化频率fN在0.83~1.0之间时,从图4(b)中可得同步整流管的导通时间和归一化频率近似呈比例关系,即

显然,系数A不是一个常数,是一个随着Q的变化而变化的量,当归一化频率fN取下限0.83时,式(22)即可表示为仅与Q有关的函数,即

关于g(Q)显性表达式可以得出,由于表达式中含有正弦、余弦的函数,工程实践中不易实现,因此可以用 f(Q)来近似代表g(Q),即两者的函数图像如图6所示。其中f(Q)是一个多项式,工程实际中比较容易实现。
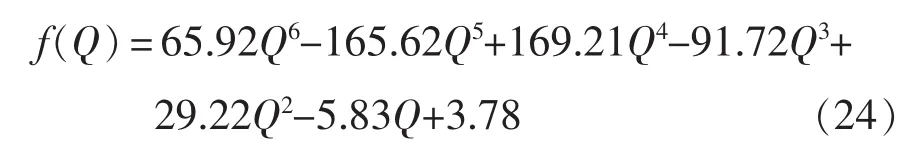
如果将式(22)视为一个线性函数,那么当Q为一个定值时,A为线性函数的斜率,表示为

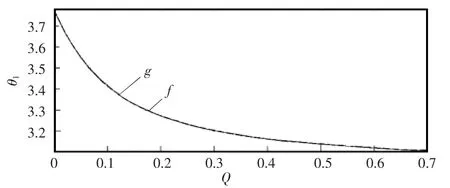
图6 g(Q)与f(Q)的函数图像Fig.6 Diagrams of g(Q)and f(Q)
当归一化频率取最小值时,由式(24)即可算出最小频率对应的θ1,从而可以得出相应的A对的值。由式(19)可得,IL与Q近似呈线性关系。所以通过检测变压器原边电流的有效值可以近似得到品质因素的大小。品质因素Q与谐振电流平均值IL的关系如表2所示,品质因素Q与导通相位θ1的关系如表3所示,导通时间t1与导通相位θ1的关系如表4所示。

表2 品质因素Q与谐振电流平均值IL的关系Tab.2 Relationships between Q and the mean value of resonant current IL
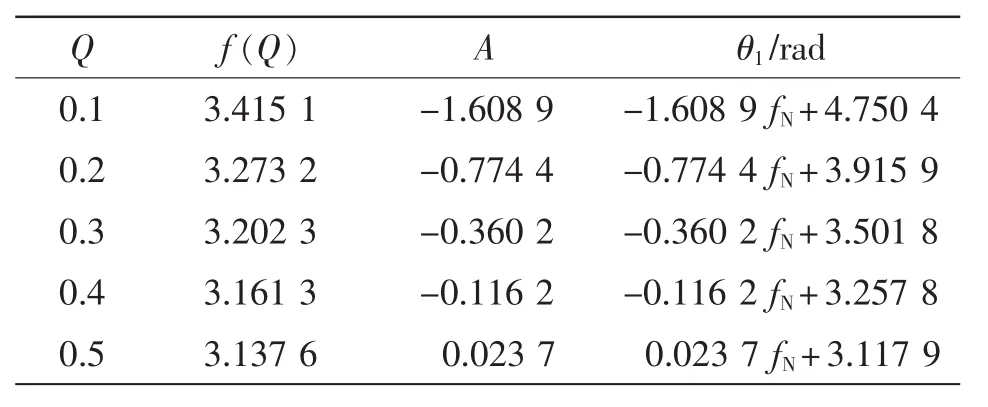
表3 品质因素Q与导通相位θ1的关系Tab.3 Relationships between Q and conduction phase θ1

表4 导通时间t1与导通相位θ1的关系Tab.4 Relationships between conduction time t1and conduction phase θ1
4 实验验证与分析
本文提出的非对称半桥LLC谐振变换器的同步整流数字控制方法在300 W的实验平台上得到了验证。当Q=0.1和0.2时,LLC变换器处于轻载工况下,此时关闭同步整流管。当Q=0.3、0.4、0.5时,SR波形如图7所示;负载由满载切换半载,半载切换满载SR波形如图8所示。本文提出的数字设计理论值为 2 816 ns、2 793 ns、2 774 ns。实验测得FPGA输出 PWM高电平分别为 2 827 ns、2 802 ns、2 777 ns。FPGA 时钟晶振为 40 MHz,受评估频率约束,不能使用PLL倍频,时间当量为25 ns,因此理论值和实验值有一定的偏差,这种偏差折合二进制2 bit左右,也是可以接受的。
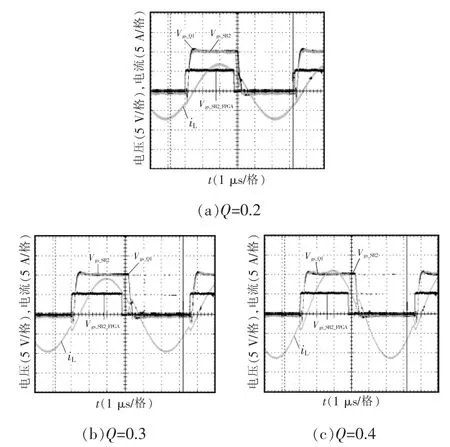
图7 不同的负载情况下同步整流管驱动波形Fig.7 Waveforms of synchronous rectifiers under different loads
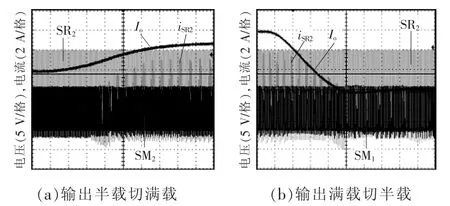
图8 负载突变SR波形Fig.8 SR waveforms under load transition
现在常用的同步整流数字算法中,欠谐振时谐振电流平台时间为,其中 Ts为开关频率,Tr为完全谐振周期;同步整流管导通时间为。因Tr是固定值,因此常用的数字算法中ton为一个固定值,不随着负载的变化而变化。副边SR关断后,电流将通过其体二极管续流,所以整机效率不能达到最优。为了避免同步整流导通时间大于副边相应支路电流持续时间而出现的副边电流反灌的现象,同步整流导通时间2.552 μs。该策略与本文中提到控制策略的效率的对比如图9所示。当处于轻载时,两种控制策略的效率是一样的,随着负载的加重,本文提到的控制策略比常用控制策略的效率要高0.5%左右。本文提出的LLC谐振变换器同步整流控制方法随着负载的变化能够自动调节相应的导通时间,是有一定的现实工程意义。
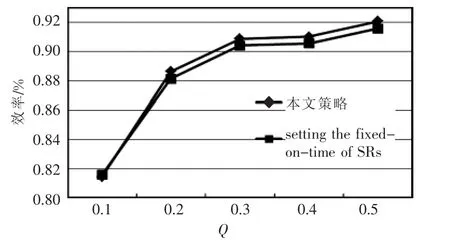
图9 两种同步整流策略的效率比较Fig.9 Comparison of efficiency under two synchronous rectification strategies
5 结语
本文对非对称半桥LLC谐振变换器进行了时域分析,建立了相应的电路模型,提出了相应的同步整流控制方法。通过检测输出电压与原边谐振电流来产生同步整流驱动,原边谐振电流的检测又能用作原边电流保护,所以这种方法不需要额外的电流互感器或者相应的外围电路。在过谐振或者完全谐振工况下,可以将同步整流驱动与原边驱动同步,在欠谐振的工况下采用本文所提的控制方法,通过300 W FPGA数控LLC变换器实验样机,与开环预设同步整流导通时间策略相比,实现效率0.5%的提升。
