基于混合储能系统的风电跟踪目标出力优化控制
2018-08-17谢志佳李建林刘昭亮
谢志佳,李建林,程 伟,刘昭亮
(1.中国电力科学研究院有限公司新能源与储能运行控制国家重点实验室,北京100192;2.天津拓鑫力神电动汽车租赁有限公司,天津300380)
风电规模化发展是我国新能源战略趋势,但由于其固有的随机性、波动性和间歇性等特征,使得大规模新能源电源的发电特性难以满足接入电网的要求,制约我国新能源发展[1-2]。大规模储能技术的引入,可以有效改善间歇式电源运行性能[3-5]。然而,风力发电出力的随机性波动分布于从秒级到小时级的广域时间尺度上,单一储能技术很难胜任风电的多时间尺度功率平抑需求和不同应用场合的应用需求[6]。
本文提出了一种混合储能系统提升风电跟踪目标出力能力的优化控制策略。该控制策略以风电功率的预测值作为风电的目标出力,通过控制混合储能系统的充放电过程来配合风电场满足相应目标出力值要求。该优化控制策略主要包括内部能量协调控制和多目标优化控制两部分,在不同储能系统的荷电状态SOC(state of charge)下采用适合的控制方法,实现了优化跟踪控制的目的。
1 混合储能系统优化过程的控制结构
由风电场和混合储能系统共同组成的风储联合发电系统,其控制的核心思想是对储能系统的能量进行合理调度以达到辅助风电跟踪发电目标的目的。混合储能系统的跟踪控制原理如图1所示。
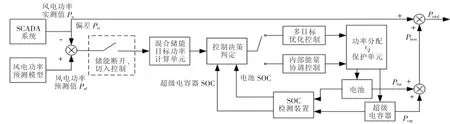
图1 混合储能系统跟踪控制原理Fig.1 Tracking control principle of hybrid energy storage system
系统有2个输入:一是风电功率的实测值Pw;另一个输入为风电功率的预测值Pwf。预测值与实测值的偏差Per=Pwf-Pw,通过一个开关控制混合储能系统是否投入运行,判定规则为

式中:Pe为风电场的额定功率;n为设定的跟踪精度。如果储能系统切入控制,Per经过混合储能系统目标功率计算单元确定混合储能系统的目标总出力值。储能系统的目标功率计算公式为


设定电池SOC的上限值为SOCbat,max=0.85,下限值为SOCbat,min=0.15;超级电容器SOC的上限值为SOCcap,max=0.95,下限值为SOCcap,min=0.05。为了避免储能系统运行过程中出现过度充电或者深度放电情况,应根据储能系统的SOC而制定相应的控制依据。如果混合储能系统的SOC都在正常合理的范围内,需制定一种优化控制策略,保证混合储能系统充分利用能量型和功率型储能各自的优势。因此,混合储能的跟踪控制包含两部分:内部能量协调控制和多目标优化控制。
2 混合储能系统的内部能量协调控制
混合储能系统的内部能量协调控制是指混合储能中电池或超级电容器单独能运行时的控制[7-9]。针对不同工况进行详细分析,并给出内部能量控制后的储能系统的功率。设在t时刻Mbat为电池储能的容量,Δt为采样时间间隔,|Pbat,lim(t)|和|Pcap,lim(t)|分别为电池和超级电容器的充放电功率限值,则内部能量控制分配的计算方法如下。
(1)SOCbat(t)<SOCbat,min且 SOCcap(t)<SOCcap,min情况
充电状态。该状态下,遵循电池优先充放的原则,先提升电池的SOC水平,剩余部分能量由超级电容器承担,功率计算公式为

(2)SOCbat(t)<SOCbat,min且 SOCcap,min≤SOCcap(t) ≤SOCcap,max情况
若为充电状态,电池SOC低于下限值,所以优先对电池充电,则有

若为放电状态,电池停止运行,由超级电容器承担放电任务,则

(3)SOCbat(t)<SOCbat,min且 SOCcap(t)>SOCcap,max情况
若为充电状态,电池SOC低于下限值,且对电池充电,超级电容器SOC高于上限值,故停止运行,有

若为放电状态,电池SOC低于下限值,对电池充电,停止运行;超级电容器SOC高于上限值,承担全部放电任务,则有
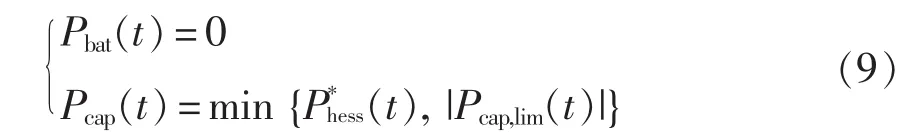
(4)SOCbat,min≤SOCbat(t) ≤SOCbat,max且 SOCcap(t)<SOCcap,min情况
若为充电状态,该状态下电池SOC处于正常运行范围内,超级电容器SOC低于下限值,所以优先对超级电容器充电,剩余部分能量由电池承担,则

若为放电状态,超级电容器停止运行,电池放电,则有

(5)SOCbat,min≤SOCbat(t) ≤SOCbat,max且 SOCcap(t)>SOCcap,max情况
若为充电状态,电池SOC处于正常运行范围内,超级电容器SOC高于上限值,故不对其充电,电池承担充电任务,则有

若为放电状态,超级电容器优先放电,电池次之,有

(6)SOCbat(t)>SOCbat,max且 SOCcap(t)<SOCcap,min情况
若为充电状态,电池SOC高于上限值,超级电容器SOC低于下限值,故电池停止动作,超级电容器充电,则有

若为放电状态,超级电容器停止运行,电池放电,则有

(7)SOCbat(t) >SOCbat,max且 SOCcap,min≤SOCcap(t)≤SOCcap,max情况
若为充电状态,电池SOC高于上限值,超级电容器SOC正常,故电池停止动作,超级电容器充电,则有

若为放电状态,电池优先放电,超级电容器次之,则有

(8)SOCbat(t)>SOCbat,max且 SOCcap(t)>SOCcap,max情况
若为放电状态,电池和超级电容器SOC均高于上限值,优先对电池放电,使其低于SOC上限值,其余部分能量由超级电容器承担,则有

3 混合储能系统的多目标优化控制
3.1 基于低通滤波的混合储能系统的能量分配
混合储能的内部能量分配规则为:超级电容器执行混合储能的功率指令中高频分量;电池负责承担长时期的低频分量,并能实时调节电容器荷电状态,以及实时响应下一指令的高频部分[10]。
本文采用一阶低通滤波器的方法,将风电功率的预测值与实测值的偏差Per分为高、低频两部分。其滤波器传递函数为

式中,τ为滤波时间常数。为方便优化计算,将滤波器从频域转换到时域,并通过其分频作用,可得t时刻电池和超级电容器的功率分别为

3.2 多目标优化模型的建立
在跟踪控制中,从储能的寿命角度来分析,应避免其“过充、深放”,应限制电池在每一个采样点的输出功率幅值,将其作为目标之一[11-12]。另外,为了满足超级电容器能够随时具有较强的高频功率输出的能力,应保持超级电容器的SOC在比较适中的水平,能够满足下一时刻充电或者放电的需求,将此要求作为第2个优化目标,即目标之二。多目标优化问题可以描述为

式中:X为待优化变量,X=(x1,x2,…,xn)T;F(X)为待优化的目标函数,F(X)=[f1(X),f2(X),…,fp(X)]T;gi(X)为约束条件;V-Min指向量最优化,即向量目标函数F(X)中各个分目标被同等级地极小化。
按照上述优化目标的要求,建立混合储能系统跟踪优化控制的模型,即

式中:SOCmed为SOC的适中水平,一般取值0.5左右;Pbat,e为电池的额定功率;Mcap为超级电容器的储能容量。式(23)表示在t时刻对电池和超级电容器的功率进行优化分配。f1为对电池功率幅值的限制,最小化在该时刻放电深度;f2为最小化超级电容的当前SOC值与SOCmed的差距,即保证超级电容器的SOC在适中的水平以应对未来时刻较高频率的输出。
多目标优化问题不存在使全部目标同时达到最优的绝对最优解,其各目标往往处于冲突状态,一个目标函数的提高需要以另一目标函数的降低作为代价。对于极小值多目标优化问题min f(X),在设计变量的可行域内,对于变量X,当且仅当不存在其他变量X*,在不违背约束的条件下满足fi(X)≤fi(X*),至少存在一个 i使得 fi(X)<fi(X*)成立,则称变量X为非支配解,即Pareto最优解[13]。
NSGA算法的非支配分类过程体现了其高效性所在,它把多目标优化问题简化至一个适应度函数的形式。该方法能解决任意目标数的优化问题,并且能求解最大或最小值的问题。NSGA-II算法是在NSGA方法的基础上改进得到一种快速的非劣性排序方法,它定义了拥挤距离,并估计某个点周围解的密度来取代适应值共享。NSGA-II算法能有效地克服NSGA的缺陷,计算复杂性从O(mM3)降至O(mM2),并具备最优保留机制及无需确定一个共享参数。该算法得到的非劣解在目标空间分布均匀,收敛性和鲁棒性好,其计算流程如图2所示。

图2 NSGA-II的计算流程Fig.2 Calculation process of NSGA-II
经图2流程计算得出的每一时刻的Pareto解集之后,需要制定出合理的决策方案,从Pareto解集之中选出满足当前决策的解。当种群数为25、进化代数为100、停止代数为100时得出Pareto最优解的情况,Pareto解集如图3所示。

图3 Pareto解集Fig.3 Pareto solution set
Pareto解的决策方法如图4所示。图中,把混合储能系统出力的一个指令周期分为两部分。在第i个指令周期Ti的后一部分周期Ti2内,为了防止下一指令周期的风电功率预测值可能会发生较大改变而导致混合储能的目标出力功率也发生较大变化的情况,因此需要在Ti2内保证超级电容器的SOC维持在一定的水平,以应对混合储能功率的高频分量,故应选取以f2较优的解作为当前解;当进入第i+1个指令周期时,前一部分周期即Ti+11内,在超级电容器负责承担一部分高频分量下,尽量降低电池的输出功率幅值,以延长储能的寿命,故应选取以f1较优的解作为当前解。

图4 Pareto解的决策方法Fig.4 Decision method for Pareto solution
4 算例分析与仿真
4.1 数据的选取及相关参数说明
以Matlab为仿真计算平台,选取99 MW风电场的功率实测值和预测值,采样时间调整为1 min,数据长度均为1 d。
电池和超级电容器的相关参数如表1所示。混合储能系统的跟踪优化控制参数如表2所示。

表1 电池和超级电容器的相关参数Tab.1 Relevant parameters of batteries and super capacitors

表2 优化控制参数Tab.2 Parameters of optimal control
4.2 仿真结果
参数设定如表2所示,令电池和超级电容器的SOC初始值均为0.5。对一天优化跟踪控制的结果进行统计分析,如图5所示。
图5(a)是风电-混合储能的各功率曲线,图5(b)是电池和超级电容器的SOC变化曲线。由图(a)可见,风电场通过储能系统的充放电作用,以风电功率的预测值作为出力目标,缩减了预测值与实测值的偏差,实现了风电、储能系统跟踪发电目标的目的。由图(b)可见,电池储能系统SOC一直运行在0.2~0.7之间,深度充放电都由超级电容器承担,充分发挥了不同储能类型的技术特性。

图5 优化跟踪控制结果Fig.5 Optimal tracking control results
加入储能前后误差指标对比如表3所示。表3中,由均方根误差 RMSE(root mean square error)、最大百分比误差MXPE(maximum percent error)和平均绝对百分比误差MAPE(mean absolute percent error)3个指标中可以更直观地看出,加入储能之后3个指标都得到了很大程度的提升,验证了在风电场中接入储能系统能够有效地改善风电场整体的出力特性,同时也提高了风电场的调度可靠性。

表3 加入储能前后误差指标对比Tab.3 Comparison oferror indicators before and after the introduction of energy storage system
图6为风电—混合储能系统各个功率在跟踪优化控制下的曲线示意。从图中可以看出,风电功率的实测值与预测值之间总是存在一定量的偏差,通过储能系统实时地根据该偏差进行充放电的作用下,使总系统的出力实时跟踪风电功率预测值,并在一定条件下满足设定的误差精度的要求。在图中区域Ⅰ部分,由于风电功率实测值与预测值偏差已经满足精度3%的要求,根据控制规则,储能系统停止运行,输出功率为0;区域Ⅱ中,电功率实测值与预测值偏差较大,已经超出储能系统能够调节的范围,按照优化跟踪控制的要求,控制储能系统尽可能出力缩减其偏差。
图7为混合储能系统内部输出功率的曲线。由图中可以看出,通过多目标优化控制不仅使电池出力尽可能小,还使超级电容器具备保持应对高频率出力的能力。由图中区域Ⅰ可以看出,根据电池和超级电容器的出力特性,通过优化控制,属于能量型储能的电池负责承担了能量的主要低频部分,而属于功率型储能的超级电容器负责高频部分的出力;区域Ⅱ部分表示电池功率已经达到了下限值,为了保护储能,限制电池出力维持到下限值。

图6 风储系统跟踪优化控制下各功率曲线Fig.6 Power curves of wind power and energy storage system under optimal tracking control

图7 混合储能系统功率曲线Fig.7 Power curve of hybrid energy storage system
5 结语
通过混合储能系统的SOC划分了不同的运行状态,针对不同的状态提出了2种不同的控制策略。一种是内部能量协调控制,保证了混合储能系统至少有一种储能装置能正常工作的情况下,合理、安全的分配电池与超级电容器间的功率;另一种是多目标优化控制,使混合储能系统在正常运行时优化了混合储能内部间的能量分配,以实现优化目标的目的。
