基于正交试验法的同心筒导流锥设计

张 晶，金 玲，张 程,2，许俊伟，宋 磊

（1．中国运载火箭技术研究院，北京，100076；2．国防科学技术大学航天科学与工程学院，长沙，410073）

0 引 言

目前，同心筒发射装置（Concentric Canister Launcher，CCL）是国内外正在研究的一种新型舰载导弹垂直发射系统[1]，采用同心布置的内外筒作为导弹的贮存、运输、发射容器。同心筒式发射装置技术为导弹、发射装置的设计提供了新的通用性，不仅质量轻、结构简单、造价低，而且可以显著地提高发射系统的性能。

1 导流锥

导流锥是同心筒发射装置中的重要组成部分，用于发射过程中对燃气流进行导流，主要作用是改变发动机喷出的燃气流的流动方向，避免在筒底产生较大的冲击[1]。对于热发射的导弹，发射过程中发动机喷管喷出的高温燃气流经导流锥导流后反流向上，利用同心筒内外筒之间的环形间隙作为排导通道向上排出。

为了研究导流型面对燃气排导的影响，文献[2]选取常见的半球型和圆锥型两种导流形式的同心筒作为研究对象，对发射过程中的温度和压力进行深入的计算和分析，得到圆锥型导流锥较半球型导流锥明显地减小了发射时筒底部的压力和温度，对发射环境起到一定改善作用。

本文以圆锥型导流锥为研究对象，对导流锥的各项参数进行优化设计，在满足发射要求的前提下，简化工艺流程、降低生产加工成本。

2 正交试验

2.1 基本概念

正交试验设计是利用正交表安排与分析多试验变量的一种设计方法。该方法在试验变量的全部参数值组合中，挑选部分有代表性的参数组合进行试验，通过对这部分试验结果的分析了解全面试验的情况，找出最优的参数组合[3]。

2.2 设计流程

正交试验设计的分析流程如图1所示，首先选取对试验影响大的因素，确定因素位级；其次根据因素和位级的多少，合理设计正交表，制定试验方案；最后对试验结果进行极差分析并得出最优方案。

图1 正交试验分析流程Fig.1 Analysis Process of Orthogonal Test

3 方案设计

3.1 确定试验因素、因素位级

本文设计的同心筒导流锥要求在发射过程中底部压力值小于0.2 MPa。针对圆锥型导流锥，在导流锥底部与发动机喷管出口距离以及外廓尺寸一定的条件下，影响底部压力值的因素有导流锥高度 H、导流锥角度θ和导流锥底部半径R，如图2所示。

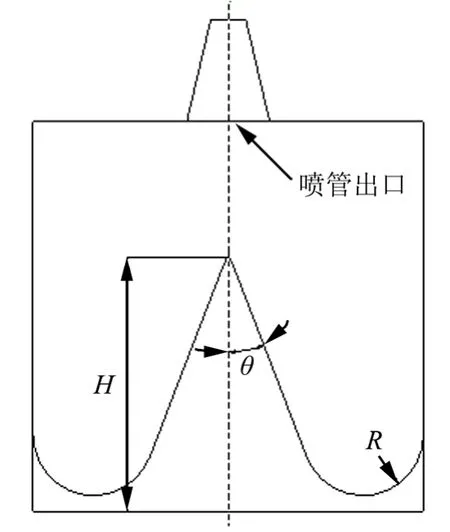
图2 圆锥型导流锥Fig.2 Conical Guide Cone

根据理论计算并考虑外廓尺寸约束范围，确定导流锥高度为400～600 mm，导流锥角度为15～25°，导流锥底部半径为130～150 mm。对以上参数选取3个位级，综合形成因素位级表，如表1所示。

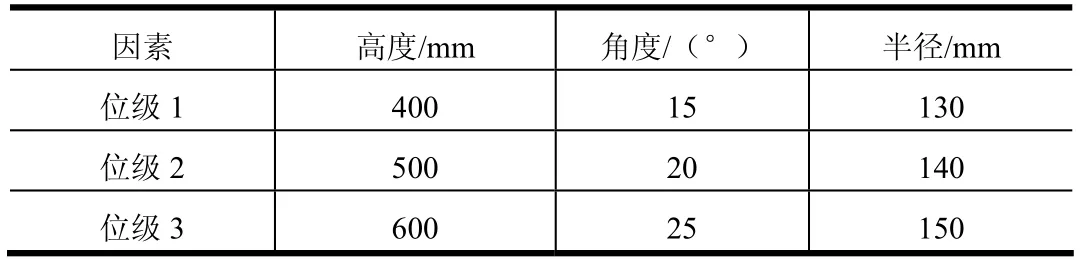
表1 正交试验的因素位级Tab.1 Factor Level of Orthogonal Test

3.2 设计正交试验表并实施试验

根据因素位级选取结果，选用L9（34）表设计本次试验，对每项试验组合进行燃气流场仿真计算，得到导流锥底部压力仿真结果，如表2所示。

表2 正交试验表及仿真结果Tab.2 Orthogonal Test Table and Simulation Results

3.3 试验结果极差分析

由表2可以看出，底部压力最低的为第2号试验，其底部压力值为0.199 MPa，3个参数（高度H、角度θ和半径R）的组合为H2θ1R1。

对正交试验仿真结果进行极差计算（以高度因素为例：位级1底部压力之和为表2中高度400 mm对应的试验号1、4、7试验底部压力之和），计算结果如表3所示，由表3可知：对于导流锥高度，位级3最好；对于导流锥角度，位级 2最好；对于导流锥底部半径，位级1最好，从而得最好方案为H3θ2R1。表3与表2仿真结果存在差距，需要进一步开展补充仿真计算。按照极差 R的大小，把因素的影响主次顺序以及优先选用的位级进行了排列，极差 R越大，因素的影响作用越大，如表4所示。

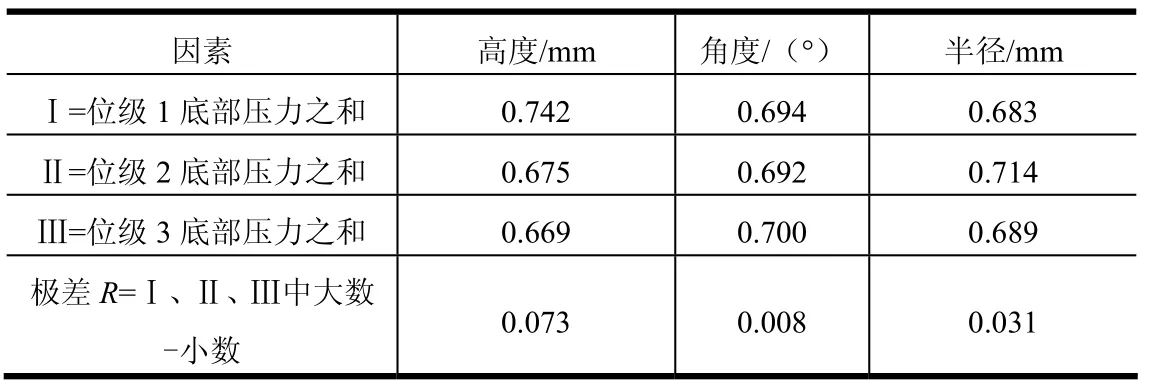
表3 正交试验仿真结果极差计算分析Tab.3 Extreme Analysis of the Simulation Results of Orthogonal Test

表4 因素主次顺序排列Tab.4 Sequence Arrangement of Factors

3.4 补充仿真计算

由于直接得出的仿真结果和极差分析结果存在差距，H2θ1R1方案和 H3θ2R1方案比较，分别为高度 H因素和角度 θ因素有差距，因此进行补充仿真计算。由表4可知，高度H因素在本次正交试验中起到的影响作用最大，角度 θ因素在本次正交试验中起到的影响作用最小，综合考虑时间周期和成本，在进行补充仿真计算时，直接选择表4底部压力低的角度θ和半径R参数，如表5所示。

表5 补充仿真计算参数Tab.5 Supplementary Simulation Calculation Parameters

对起主要作用的高度H因素选取两组参数进行进一步仿真计算，高度H因素参数和底部压力仿真计算结果如表 6所示，Fluent燃气流场仿真压力云图分别如图3、图4所示。

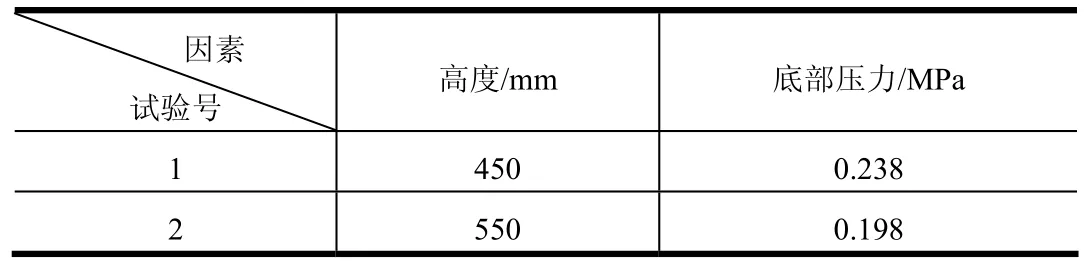
表6 补充仿真计算结果Tab.6 Supplementary Simulation Results

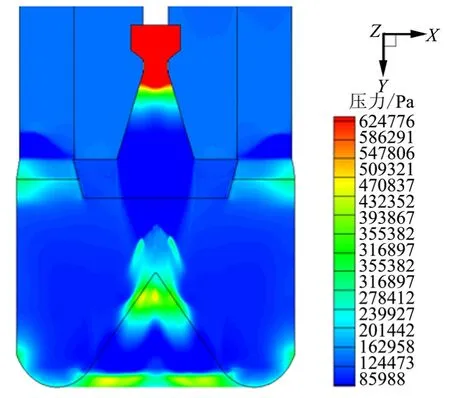
图3 高度450mm压力云图Fig.3 Height 450mm Pressure

图4 高度550mm压力云图Fig.4 Height 550mm Pressure

3.5 结果分析

由表2、表3可知，在导流锥底部与发动机喷管出口距离以及外廓尺寸一定的条件下，导流锥底部压力值随着高度H、角度θ、半径R的增大呈现出先降低后升高的趋势，由于3个参数相互关联，本次正交试验仿真子样数量较少，因此该结论不具有普遍性。

由表 6可知，第 2号试验的底部压力值为0.198 MPa，达到设计要求，可以得出圆锥型导流锥型面的主要设计参数为：导流锥高度H为550 mm，导流锥角度θ为20°，导流锥底部半径R为130 mm。

在补充仿真计算过程中仅选取了两个不同的高度参数进行比较，未进行进一步深入细化仿真，因此得到的最终设计参数仅为优选后的结果，不一定为最优解。

4 产品加工与发射试验

根据设计参数进行导流锥产品加工，金属件加工完成后在表面喷涂防热涂层，产品实物如图5所示。该导流锥产品参加了同心筒发射试验，试验过程中对导流锥底部压力进行测量，底部压力实测值为0.18 MPa，满足设计要求。

图5 导流锥产品Fig.5 Guide Cone Product

5 结 论

本文采用正交试验方法对同心筒导流锥进行设计，针对影响底部压力的高度、角度、底部半径3个参数进行试验设计与仿真计算，最后通过补充仿真计算得到优化参数组合，达到设计要求。对按照设计参数生产加工的导流锥产品在同心筒发射试验过程中进行底部压力值测量，结果表明满足设计要求。