在险价值度量方法及应用研究
2018-08-16
1.引言
在正常的非极端的市场条件下,一定的金融资产或投资组合在给定的持有期内和在一定的置信水平(confidence level),通常是95%或99%,所发生最大可能的损失。由此可知,置信水平对于VaR具有较大的影响,对于相同的投资组合,置信水平越高,所计算的VaR值越大,估计的VaR出现相应风险的概率越小。
用数学表达式来表示:设pt是该资产组合在t时刻的价格,pt+1为该资产组合在持有Ⅰ期后的价格,在置信水平1-α下最大可能损失VaR可以表示为:
prob(pt+1-pt<-VaR)=α
(1.1)
VaR的计算是目前在险价值研究的核心问题。 Manganelli S.(2001)提出VaR模型的计算方法主要分为三类:参数法、非参法和半参法。参数法包含风险度量制和GARCH模型等;非参法有历史模拟法和混合模型;而极值理论、分位数回归模型均归类于半参模型。
2. 模型构建
2.1 方差-协方差
利用方差-协方差方法(Variance and Coveriance method)计算VaR的步骤如下:
首先根据历史数据计算出资产组合收益的波动和线性相关关系;再根据一定畳信水平,找到对应的分位数,该分位数反映了收益偏离均值的临界值;然后建立与市场因子的联系,推导出VaR值:
(2.1)
其中:Zα为标准正态分布下置信度α对应的分位数;σ为组合收益率的标准差;Δt为持有期。根据上式可知,VaR的计算中有两个重要的参数:持有期Δt和置信水平α。
关于σ的估计,J.P. Morgan(1995)提出指数移动平均法(EWMA),此方法考虑了数据的波动性与相关性,降低了“幽灵效应”和数据波动的“聚集性”。所谓幽灵效应,是指由于等权重,造成极端值对波动性产生长时间的影响,致使估计偏差的产生。方差的指数移动平均估计公式为:
(2.2)
其递归形式为:
(2.3)
方差-协方差法的计算较为简单、直观,但大多数金融资产的收益率数据呈尖峰、厚尾特征,方差-协方差法无法预估极端事件的风险,因此求得的在险价值往往会被低估。
2.2 历史模拟法
历史模拟法(Historical simulation method)的假设前提为市场因子的未来波动率与其历史波动率相一致,其度量步骤为:首先找出合适的证券投资组合市场因子的历史收益率时间序列[Rt(t)],t=-T,-T+1,L,0;再将组合收益从小到大排序,得到证券组合未来的损益分布;然后根据损益分布及给定的置信度95%或99%选择相应的分位点,得到该证券组合的在险价值。
历史模拟法计算较为简便,作为非参数完全估值法,能够较好地处理非线性问题。但是它假定过去的数据能很好的描述未来的情况,并假设收益服从独立同分布,这与实际并不相符;并且其结论质量在很大程度上与历史周期长度相关。
2.3 蒙特卡罗模拟法
蒙特卡罗模拟法(Monte Carlo simulation method,MC)和历史模拟法理念相似,区别在于其资产收益率或风险因子收益率不是历史观测值,而是计算机模拟的虚拟结果。
几何布朗运动的离散形式可表示为:
(2.4)
其中ΔSt+1=St+1-St,St表示t时刻的资产价格,St+1表示t+1时刻的资产价格,N×Δt=T,μt表示资产收益率的均值,σt表示资产收益率的标准差,εt表示随机变量。这里εt∶N(0,1)。
根据t分布依次产生相应的随机序列,并计算模拟价格St+1,St+2,K,ST
(2.5)
(2.6)
(2.7)
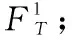
蒙特卡罗模拟法可以处理非线性、非正态的厚尾和波动剧烈的金融资产。但由于依赖于历史数据,容易存在模型风险和参数估计的偏差。
3. 实证分析
3.1 样本来源及处理
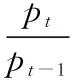
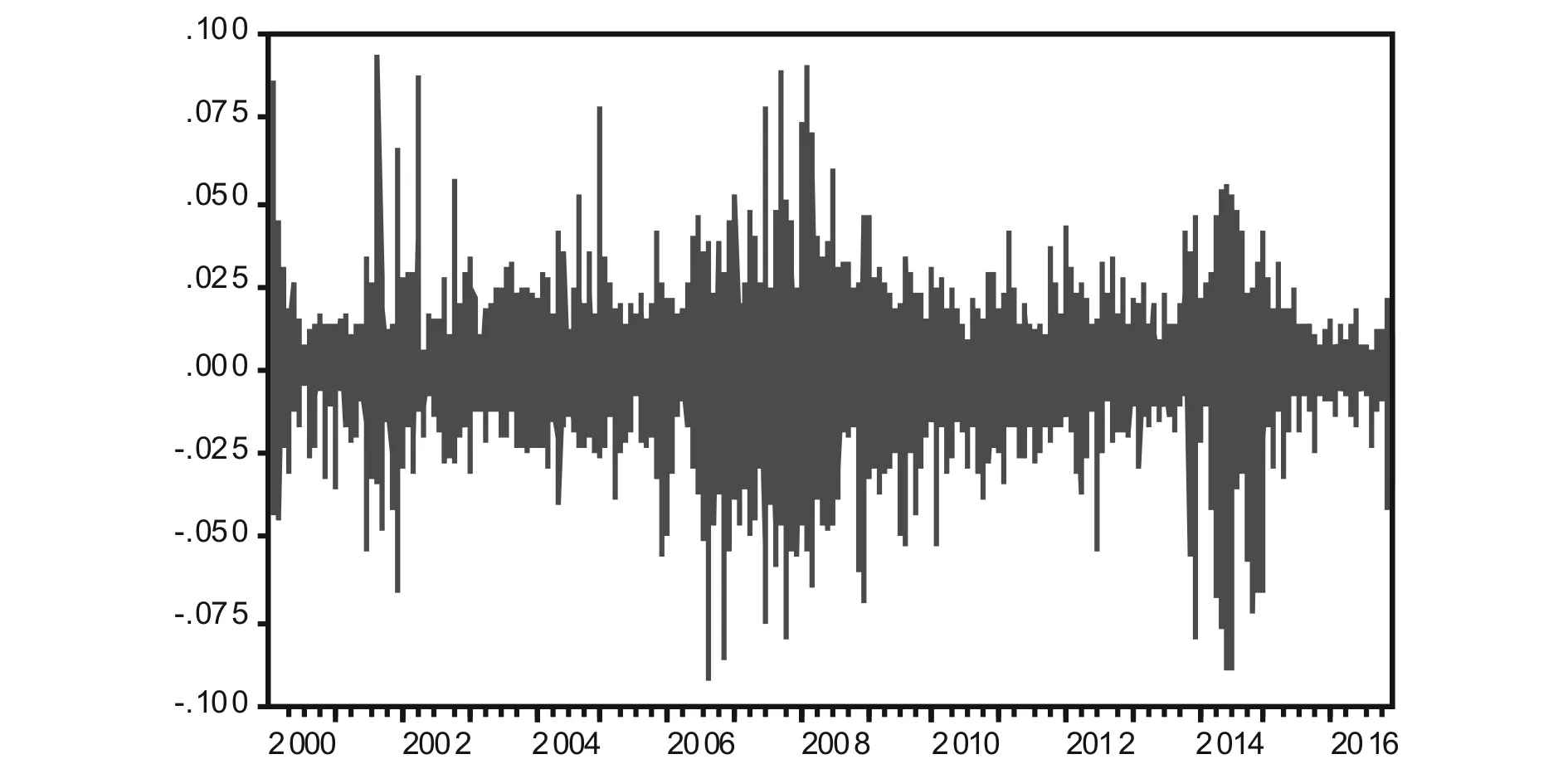
图3.1 上证指数日收益对数直线图
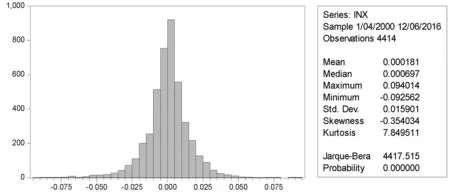
图3.2 上证指数日收益对数统计结果
对自然对数收益率的分布进行检验,统计结果见图3.2,均值u为0.000181,标准差σ为0.015901,偏度S为-0354034,峰度K大于3为7.849511。
3.2 方差-协方差法
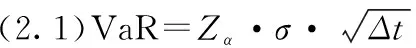
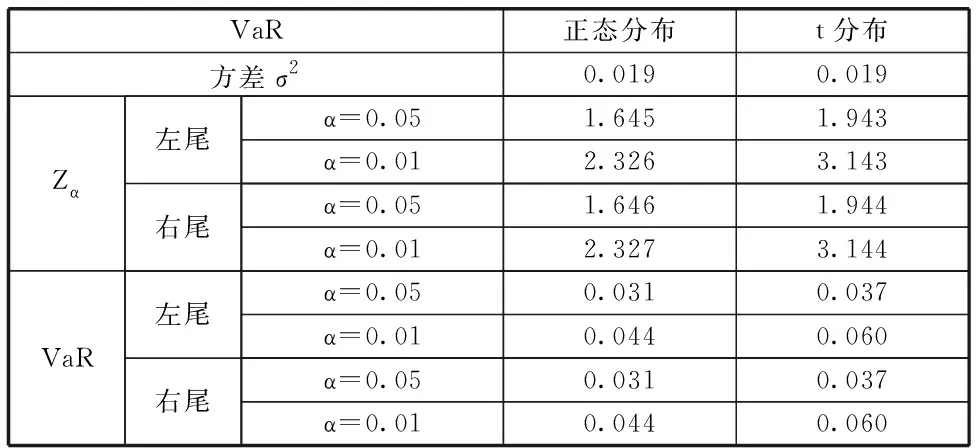
表3.1 方差-协方差法计算的VaR结果
3.3 历史模拟法
选取2013年3月28日到2018年3月28日上证指数共1217个日对数收益数据,按从大到小降序排列,求分位数α==0.05和α=0.01下的损益值,分别是左尾和右尾情景的第61(1217×5%≈61)和第12个数(1217×1%≈12),结果如表3.2所示:

表3.2 历史模拟方法计算VaR结果
3.4 蒙特卡罗模拟法
从4414个收益对数中随机选取100个随机数。根据几何布朗尼运动模型,重复1000次,使用蒙特卡罗方法计算出风险价值,降次排序后的第100×α个模拟价格(100×5%=5,100×1%=1)。

表3.3 蒙特卡罗法计算VaR结果
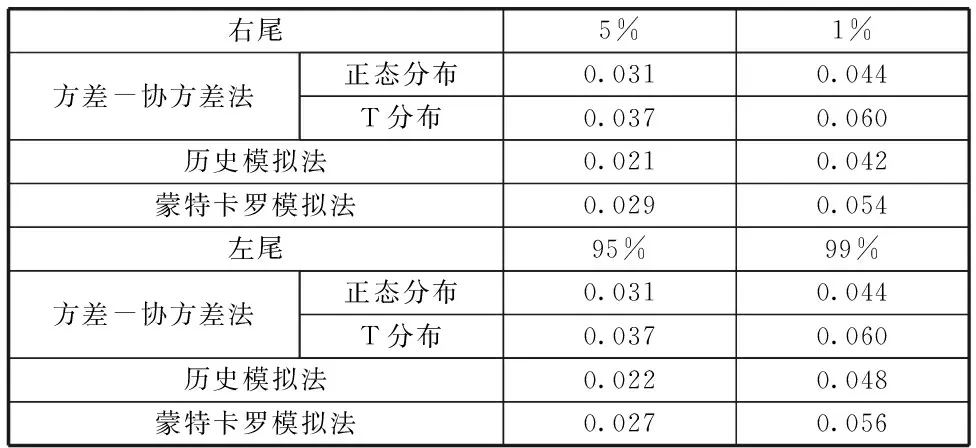
表3.4 VaR结果对照表
表3.4是利用方差-协方差方法、历史模拟法和蒙特卡洛模拟法分别求得的VaR的对照表,可知:
在分位数5%的情况下,历史模拟法求得的值最小;分位数是1%的情况下,历史模拟法和正态分布的方差-协方差法所求的值较小;T分布下方差-协方差法的值在分位数5%与1%时,均为最大值。
4. 结论
本文通过对方差-协方差方法、历史模拟法和蒙特卡洛模拟法这三种方法的实证应用研究发现在不同的置信水平上,计算所得的VaR不同。
由检验结果可知:上证收益率分布不服从正态分布,存在厚尾特征。如近似将其看作正态分布,则计算出来的在险价值结果会被低估。虽然传统计算方法也可以被改进,例如对方差-协方差方法采用t分布假设和指数移动平均估计,以更加贴近真实的金融市场价格波动情况,然而依然无法解决分布的“厚尾”问题。
