残差字典学习的快速图像超分辨率算法*

王建新，吴宏林，张建明，殷苌茗

1.长沙理工大学 综合交通运输大数据智能处理湖南省重点实验室，长沙 410114

2.长沙理工大学 计算机与通信工程学院，长沙 410114

1 引言

图像超分辨率（super-resolution，SR）重建是由输入的一个或者多个低分辨率（low-resolution，LR）图像恢复得到高分辨率（high-resolution，HR）图像[1]。由于输入的低分辨率图像提供的信息有限，图像超分辨率重建是一个典型的病态逆问题，需要相关的先验信息[2]。现有超分辨率方法大致可分为3类：基于插值的方法[3]、基于重建的方法[4]及基于学习的方法[5]。基于插值的方法用多项式充分近似表示，方法简单易行、速度快，但是图像模糊、质量差；基于重建的方法通过对未知的高分辨率像素值施加一组线性约束，能有效保持边界尖锐和抑制伪影，但是当放大因子较大时重建效果较差；基于学习的方法通过学习训练图像，充分利用图像固有的先验知识恢复的图像效果较好，是目前较为常用的方法[6]。

近年来，随着压缩感知和机器学习研究的进一步深入，针对基于学习的超分辨率方法，已有许多学者展开研究并取得了一系列成果。Yang等人[5]将压缩感知理论与稀疏编码相结合，提出基于稀疏表示的图像超分辨率算法，该算法利用外部训练图像集学习得到一对LRHR字典，求解出低分辨率图像块在LR字典中的稀疏系数，再利用稀疏系数与HR字典结合重建高分辨率图像。在后续研究中，Yang等人[7]提出了基于稀疏编码和联合字典学习的超分辨率（image super-resolution via sparse representation，ScSR）算法，进一步提升了图像超分辨率的重建质量和速度。Glasner等人[8]提出了一种基于图像自相似性的单幅图像超分辨率算法，通过对输入图像进行不同尺度的插值来产生样本库，但是自适应能力差，重构的图像伪影严重。Marco等人[9]鉴于超分辨率重建恢复的是图像的高频信息，提出了基于反投影残差图的相邻嵌入超分辨率算法，通过构造一对新型字典重构出高分辨率图像。Zhu等人[10]对字典进行了进一步改进，提出基于自学习和稀疏表示的快速单图像超分辨率（fast single super-resolution via selfexample learning and sparse representation，CS-SR）算法。该算法使用K次奇异值分解（Ksingular value decomposition，KSVD）算法由图像自相似块来构建学习字典，在重构阶段使用简单的正交匹配追踪（orthogonal matching pursuit，OMP）算法对图像进行稀疏编码，在重建质量和速度上都有所提升。

在上述常见的基于学习的超分辨率重建算法[5,7,9-10]中，字典学习起着关键作用。基于学习方法的字典对通常由训练图像集中具有相似统计特征的图像随机取样生成，从其来源可分为两大类：内部字典和外部字典[11-12]。一般图像通常具有大量的自相似性，内部字典则由输入图像本身的自相似冗余块构建，基于内部字典的超分辨方法由于图像本身提供的信息有限，在超分辨率重建中内部图像块之间不匹配，从而导致过多的伪影[13]。外部字典则是通过对外部训练图像集随机采样生成的，它包含的特征信息丰富，能很好地重构出高分辨率图像，与内部字典每次在线生成不同的是，外部字典是预先建立的，可极大减少重建过程的计算量和时间[12]。

针对基于自学习和稀疏表示的快速单图像超分辨率[10]重建图像伪影明显、执行效率低的问题，本文提出了残差字典学习的快速图像超分辨率算法，在学习字典前先对外部训练图像集中的HR图像进行预处理，提取其高频残差图，再利用Yang等人[7]的字典训练方法学习得到一个高频残差字典，使字典学习不再局限于单一的重建模型，降低了计算量，并提高了字典训练的精度。用基于Cholesky分解的正交匹配追踪算法求解稀疏系数，将求得的稀疏系数与高频残差字典结合应用于重建阶段，不仅有效降低了运算时间，还提高了重建质量。再用迭代反投影（iterative back projection，IBP）法[9]对重建的图像进行迭代计算，在一定程度上减少了重建误差。实验结果表明，本文算法不仅有效降低了字典训练时间和图像重建时间，同时还进一步提升了重建图像的质量。

本文组织结构如下：第2章介绍了相关工作；第3章对残差字典学习的快速图像超分辨率算法进行详细阐述；第4章为实验与分析；最后是结束语。

2 相关工作

传统的图像超分辨率重建算法，对图像的处理可以看成是传统图像处理算法的逆过程，是一个典型的病态逆问题。由于LR图像Y可以看作是由HR图像X通过模糊化B、下采样D以及添加噪声v得到，Y=BDX+v，因此为了得到更为合理的解，可以通过添加先验约束条件来解决该问题[6]。目前深度学习技术已成功地应用于计算机视觉的许多领域，包括低级别的图像恢复问题。最近提出的几种基于深度神经网络的图像超分辨率重建模型[6,14-16]，取得的卓越性能超越了以往的机器学习模型，但传统的稀疏表示方法仍是有价值的，本文方法就是基于稀疏表示的超分辨率重建模型。

2.1 基于稀疏表示的超分辨率重建算法

自然图像的局部结构信息可以近似地由样本特征库中的一组图像块线性表示出来，不同的结构信息其线性组合也不同。基于稀疏表示的图像超分辨率重建算法[7]，利用输入的低分辨率图像分割成的图像块求解出一组线性原子，从而恢复出目标高分辨率图像。将一幅图像Y分割成若干图像块后，每个图像块作为一组输入样本向量y，存在包含K(K＞n)个原子的过完备稀疏字典DL∈Rn×K，使得输入的每个图像块y都可以在字典DL中线性表示出来：

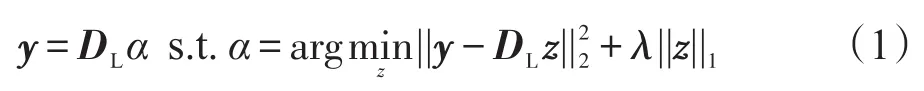
其中，||·||1用于保证稀疏性；||·||2表示重构误差；λ表示正则化系数。算法假设低分辨率图像块y和高分辨率图像块x在过完备字典DLDH中能用同一个稀疏系数α线性表示出来，因此对任意输入的低分辨率图像块y，其对应的目标高分辨率图像块x都可以表示为：

在图像重建阶段，由于存在噪声，直接组合重建的高分辨率图像可能不会满足重建约束和稀疏先验约束。为了获得质量更好的重构图像，还会引入局部先验约束和全局约束[7]。

基于稀疏表示的超分辨率算法中需要解决的关键问题主要有两点：（1）通过训练，采用何种学习方法获得低分辨率图像与高分辨率图像之间的对应关系；（2）稀疏字典对的生成。

2.2 联合字典对训练

联合字典训练阶段的主要目的就是为了获得过完备的低分辨率字典DL和高分辨率字典DH，使得LR图像块和HR图像块的稀疏编码系数是相同的。由于超分辨率重建的病态性，使得联合字典的生成是一个复杂问题[17]。对于给定的外部HR图像训练集XH={x1,x2,…,xn}，对其每幅图像进行模糊化和下采样操作得到对应的LR图像集YL={y1,y2,…,yn}。为了提高图像的重建精度，通常会提取外部LR图像块的不同特征信息，Yang等人[7]利用LR图像块的第一和第二阶导数来提取其特征信息，用于提取特征信息的4个滤波器分别为：

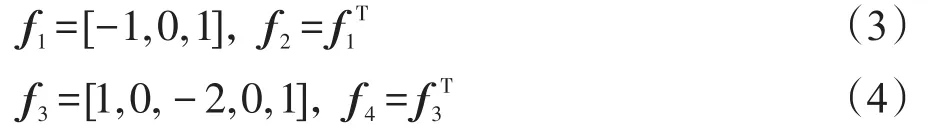
其中，T表示转置，将4个滤波器直接作用于外部训练集中的每个LR图像得4个梯度图像，再在每个梯度图像的相同位置提取特征图像块，将产生的4个图像块串联起来作为特征向量。因此每个LR图像块的特征向量都包含了其邻近的编码信息，这有利于促进最终输出HR图像的内部相邻块之间的兼容性。其中单一字典训练的公式为：

Yang等人[7]结合这些目标，对外部HRLR图像同时进行训练，将两个特征空间的求解问题转换为一个标准的单特征空间的字典训练问题，求解得到的HR字典和LR字典共享稀疏系数：

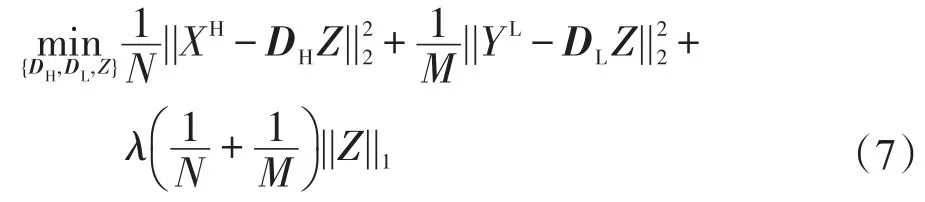
其中，N和M分别表示HR字典和LR字典矢量形式的维度；||·||1用于增强稀疏性；||·||2用于约束字典的列和除去缩放误差。该算法只需训练一次就可以得到两个字典。

2.3 迭代反投影法

本文在超分辨率重建之后增加了一步迭代反投影操作。迭代反投影（IBP）法使输出的高分辨率图和输入的低分辨率图保持一致性，且能修正SR过程中产生的误差[9,12]，该操作使输出的高分辨率图像沿着正确的方向发展。在SR算法执行之后，将生成高分辨率图像XH和最初输入的低分辨率图YL同时作为迭代反投影算法的输入项，经迭代后得到的最终高分辨率图像̂H与最初的输入图像YL在结构上保持一致性。XH通过计算输入的LR图像YL与HR图像YL=(XH∗b)↓m的反投影误差，在迭代过程中不断得到修正[9]。这种迭代反投影法的更新方程为：

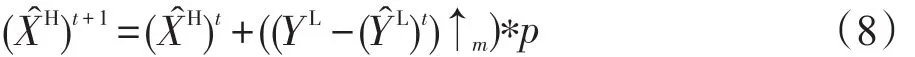
第t次迭代时的LR图是由与之相关的HR图反投影得到的，p是一个局部传播差分误差的反投影滤波器，m为缩放因子，↓是下采样符号。本文经过多次实验验证，最高迭代次数t=10时重建的图像质量效果最好。

3 残差字典学习的快速图像超分辨率算法

本文充分利用外部图像集的附加高频信息和稀疏表示重建的优势，提出了残差字典学习的快速图像超分辨率算法。算法分为两个阶段：字典训练阶段，首先对外部训练HR图像集XH={x1,x2,…,xn}进行插值缩小，得到对应的LR图像集YL={y1,y2,…,yn}，再用双三次插值和迭代反投影法获得外部HR图像的高频残差图，最后用Yang等人[7]的字典学习算法构建高频残差字典和低分辨率字典。重建阶段，先将低分辨率图像用双三次插值放大得到伪高分辨率图像，对于图像中的光滑区域，双三次插值方法可以产生较好的效果，但是却无法恢复出图像的高频信息，因此伪高分辨率图像还是低分辨率图像。再用基于Cholesky分解的正交匹配追踪算法快速求解出稀疏系数，将求得的稀疏系数与高频残差字典相结合重建出高频图像，融合高频图像和伪高分辨率图像得到高分辨率图像，最后用迭代反投影法对融合图像进一步修正，输出目标高分辨率图像。

3.1 残差字典的生成

在字典训练过程中，对于外部HR训练图像集XH={x1,x2,…,xn}，Yang等人[7]的方法是通过预处理对其中的每幅图像进行模糊化B和下采样D操作，得到对应的LR图像集YL={y1,y2,…,yn}。然后再对HR图像进行随机取块得到HR字典，对LR图像先插值放大再随机取块得到对应的LR字典，其流程如图1所示。相对于光滑平坦的区域，自然图像中的边缘、纹理等特征区域结构变化较为明显，而人的视觉系统对高频区域变化比较敏感，因此图像高频特征区域的结构信息对于超分辨率重建非常重要。在图像超分辨率重建过程中实质上恢复的是图像的高频信息，使用和合并图像的高频信息能给输入LR图像提供更真实的高频信息[18]。

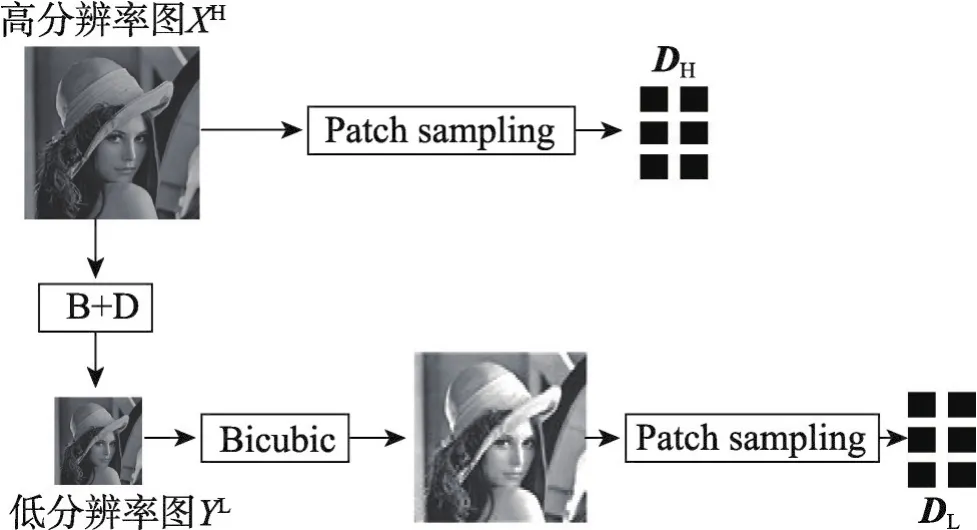
Fig.1 General dictionary training model图1 常规的字典训练模型

基于外部HR图像集的字典学习，当训练样本数比较庞大时，传统的字典训练模型需要同时学习外部HR图像的高频信息和低频信息，导致KSVD算法的计算复杂度很高。通常高分辨率图像可以分解成两部分：低频信息部分（即输入的低分辨率图）和高频信息部分（对应残差图）。其中高频部分包含了图像的高频细节和纹理特征等结构信息[19]。本文根据超分辨率重建过程中需要恢复的是图像的高频细节部分，利用高频残差图的思想[9]将残差字典引入基于稀疏表示的图像超分辨率重建过程，通过对外部训练HR图像进行预处理，单独提取出高频部分进行取块训练，以减少字典学习过程中的计算量，降低字典训练的时间复杂度。在字典学习过程中的外部图像预处理阶段，外部HR图像集中的任一图像XH先经模糊化B和下采样D处理后得到对应的LR图像YL,对图像YL进行插值放大和迭代反投影处理得到相应的插值增强图像F(YL)，最后通过求HR图像XH与插值增强图像F(YL)的差值(XH-F(YL))，得到HR图像的高频残差图。这一步操作类似于通过一个高通滤波器，得到的高频残差图包含了图像的结构信息和高频细节信息。通过对高频残差图的取块得到对应的高频残差字典，与传统字典学习方法对比，高频残差字典在训练阶段将低频部分过滤掉，仅对图像的高频部分进行训练，既减少了字典训练的计算复杂度，又提升了字典的重构能力。高频残差字典的训练流程如图2所示。

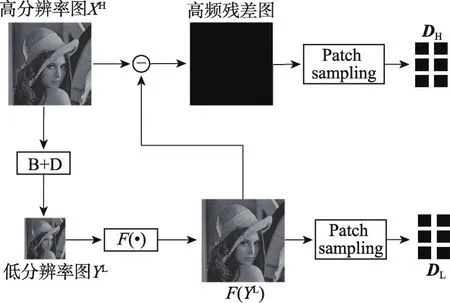
Fig.2 Training model of residual dictionary图2 残差字典的训练模型

3.2 基于Cholesky分解方法改进的正交匹配追踪算法

正交匹配追踪算法[20]是稀疏表示的一种经典的也是最简单的算法之一，它的目的是为了求得式（1）中α的最逼近解。该算法通过贪婪迭代的方法选取压缩感知矩阵中与信号相关性最大的列向量，这里压缩感知矩阵可以理解为原子库，而列向量则为原子库中的原子。OMP算法需要两个输入，测量矩阵DL和测量向量y，最后得到稀疏度为K的原信号估计α。残差在OMP算法中是一个重要的度量量，对于残差信号r的控制体现了匹配追踪算法的核心思想。在每次迭代过程中，选出测量矩阵DL和残差r最匹配的原子，然后通过消除该原子的贡献来计算新的残差，并得到一个新的估计，经过t次迭代逐步实现对原信号的逼近，由此完成重建过程。基于正交匹配追踪算法的重建步骤如下：

输入：测量矩阵DL，测量信息y，稀疏度K。

输出：稀疏表示α。

初始化：残差r=y，稀疏度K=size(DL,1)/4，索引集P0=ϕ，迭代次数t=1。

（1）求得索引jk：计算残差与感知矩阵的每一列的内积，并选择最大的幅值对应的索引，即满足

（2）更新索引集和原子集：

（3）利用最小二乘法计算近似解：

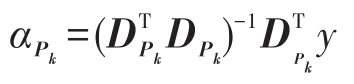
（5）判断迭代次数是否满足t＜K，如果满足则迭代终止，α=αPk，r=rk，否则重复第（1）步。

（6）利用Cholesky方法快速计算近似值：

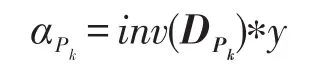
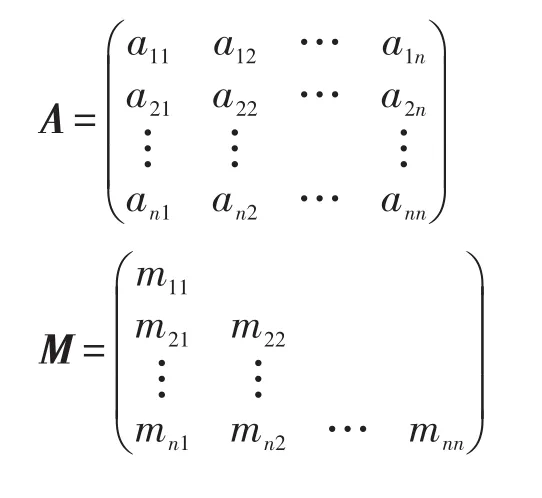
Cholesky分解方法[21]的基本原理：假设初始训练数据N0，如果n阶方阵A的顺序主子式均不为0，则N0=N有唯一的分解，即A=MN。其中M是单位下三角阵，N是上三角阵。若A是n阶的对称正定矩阵，那么A也满足MN分解，并且可以分解为下三角矩阵M和转置矩阵MT的乘积，即：

那么上式即为对称正定矩阵A的Cholesky分解。其中A为对称正定矩阵，矩阵M不一定是单位下三角矩阵。

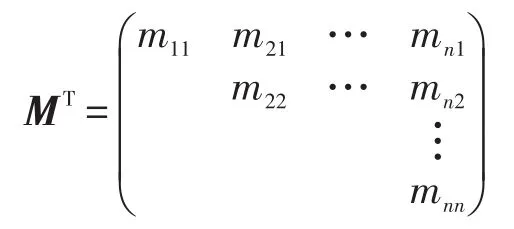
第一步：由式（9）计算可得矩阵M的第一列所有元素：

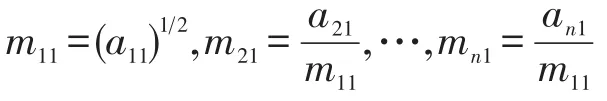
第二步：再比较式（9）两边第二列对应的元素得到：

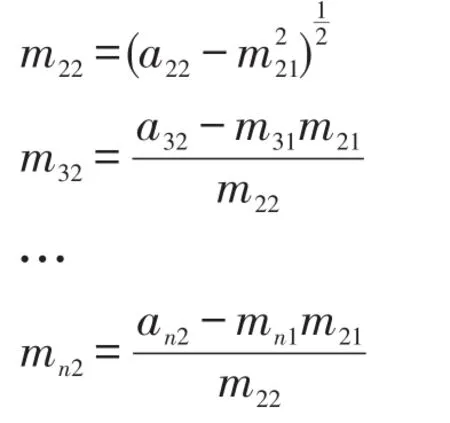
第N步：同理由式（9）以此类推：

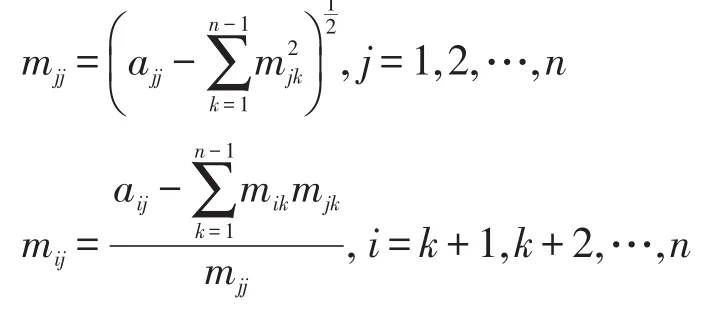
上式分别计算的是矩阵M第j列主对角元素和第j列第i行的所有元素，由此可以确定矩阵的所有元素，这就是Cholesky算法。

3.3 本文算法步骤

本文设计的残差字典学习的快速图像超分辨率算法步骤如下：

步骤1对训练HR图像用双三次插值和迭代反投影法进行处理，得到对应的LR图像集，并提取外部训练HR图像的高频残差图，用Yang等人[7]的字典学习方法训练得到残差字典和低分辨率字典。

步骤2对需要超分辨率重构的LR图像YL用双三次插值放大，得到伪高分辨率图像YH。

步骤3提取伪高分辨率图像YH的特征块y。

步骤4利用基于Cholesky分解的OMP算法求得的稀疏系数α=OMP(DL,y)，算法中迭代终止的条件为迭代的次数小于或等于size(DL,1)/4。

步骤5联合残差字典DH和稀疏系数α求得目标HR图像的高频特征图为x=DHα。

步骤6融合伪高分辨率图YH和高频特征图x得高分辨率图像HR=YH+x。

步骤7对融合图像用迭代反投影法处理完成超分辨率重建。

4 实验与分析

在本文实验中，使用与文献[22]相同的数据和协议进行对比，这些数据和协议都是目前图像超分辨率算法中常用的[7,9]。外部高分辨率图像通过双三次插值缩小的方式，生成用于训练和实验评估的低分辨率图像。训练图像集的扩增通过图像的转换、旋转和比例缩放等实现。本文采取峰值信噪比（peak signal to noise ratio，PSNR）对重建图像质量进行评估，PSNR越大，重构图像质量越好。本实验程序在4.0 GHz CPU及16 GB内存，Win 7操作系统，PC环境上采用Matlab R2015b软件进行图像超分辨率处理。

为了丰富实验的数据，本文在视觉效果和运行时间两方面进行对比，实验中以双三次插值算法作为基准对比算法，并选取最近的5种SR算法进行对比实验：ScSR重建算法[7]、CS-SR算法[10]、基于卷积稀疏编码的超分辨率（convolutional sparse coding for image super-resolution，CSC）算法[23]、基于深度学习的超分辨重建（image super-resolution using deep convolutional networks，SRCNN）算法[14]和基于锚定邻域回归的快速超分辨率（anchored neighborhood regression for fast example-based super-resolution，ANR）算法[22]。对比内容包括峰值信噪比（PSNR，dB）和重建时间（s）。任选测试图像集set5和set14中的6张不同图像进行2倍超分辨率重建对比。为了公平对比，从这些作者的个人主页上下载Matlab源代码，用原作者提供的参数设置进行实验。由于人类视觉系统对亮度变化比较敏感，将彩色图像由RGB颜色空间转换到YCb-Cr颜色空间，对Y通道即亮度通道用不同超分辨率方法处理，Cb、Cr彩色通道用Bicubic方法处理。在实验过程中，先对256×256像素的真实HR图像进行插值缩小得到输入的测试LR图像128×128，再对其进行图像超分辨率重建。图3和图4是本文的SR算法和其他SR算法的效果对比图。

由图3、图4可以看出，7种算法在光滑区域重建效果基本相同。在边缘和不规则结构区域，ScSR算法[7]较双三次插值算法细节部分清晰，但是边缘区域伪影明显，且图像的纹理细节产生了轻微的扭曲；CS-SR算法[10]图像部分高频信息丢失，导致生成的图像伪影明显，有锯齿效应；CSC算法[23]的边缘部分出现平滑和伪影效果，细节部分也不够清晰；SRCNN算法[14]在边缘和不规则结构区域细节模糊，锯齿效应明显；ANR算法[22]在边缘区域过于模糊，伪影明显；本文算法在消除伪影的同时，不仅能保持图像边缘的锐度，还能较好地恢复出图像的纹理细节。

Fig.3 Super-resolution reconstruction results of“mlena”with scale factor 2图3 mlena图像2倍时的超分辨率重建结果

本文的参数设置和文献[10]相同，从样本中随机抽取10 000个图像块以构成训练集，图像块大小为8×8，字典大小为64×64，稀疏平衡因子为0.15，保留1个像素的重叠。与文献[7]抽取100 000个图像块，字典大小为25×512和图像块大小5×5相比，本文算法字典的训练时间更短，计算复杂度更小。表1是6幅测试图像在各种SR算法中，放大倍数为2时的重建时间。

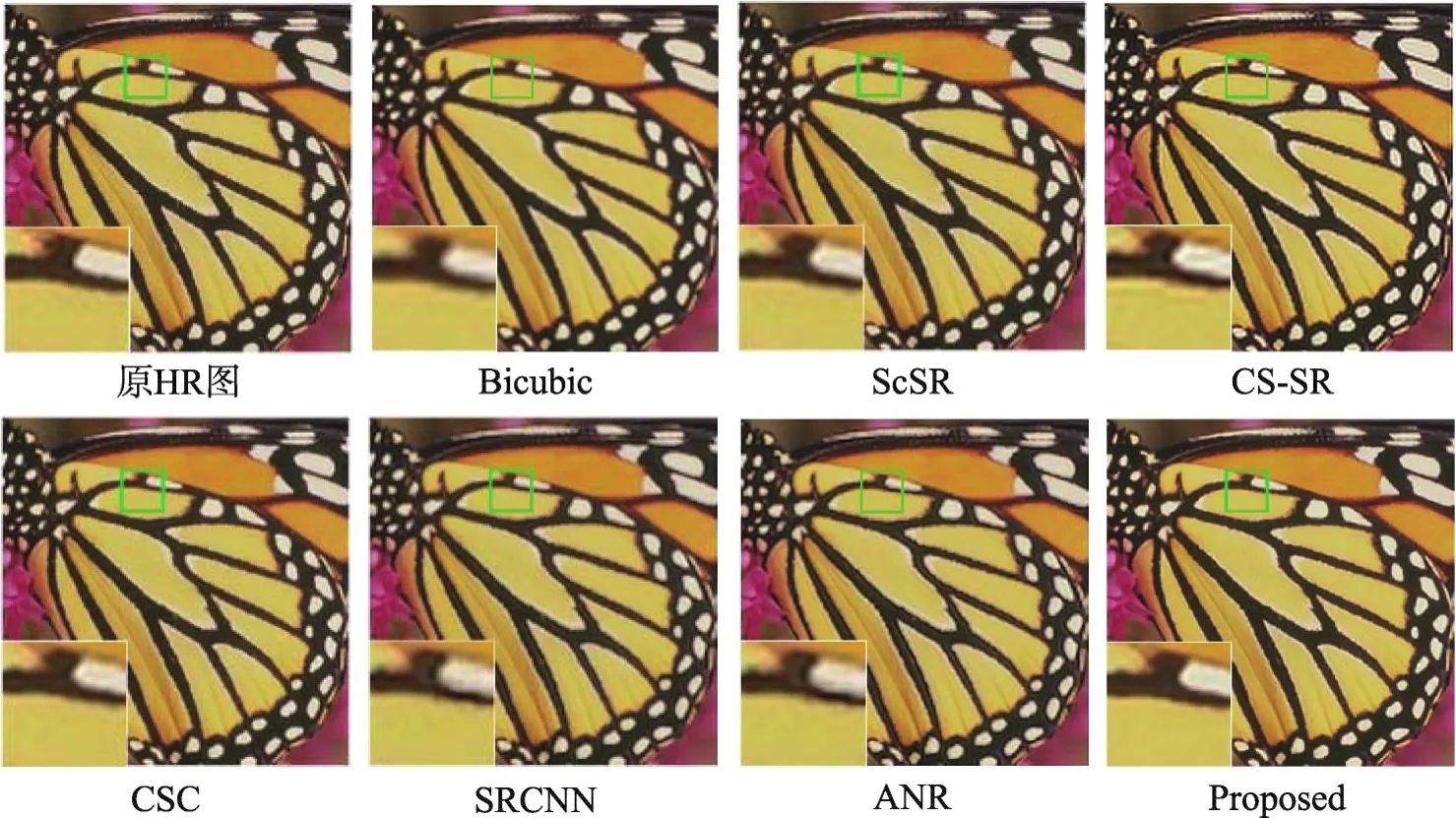
Fig.4 Super-resolution reconstruction results of“butterfly”with scale factor 2图4 butterfly图像2倍时的超分辨率重建结果

Table 1 Reconstruction time of different SR algorithms表1 不同SR算法重建的时间 s

在重建时间上，不考虑字典训练时间，仅仅对各种SR方法的图像重建时间进行比较。本文使用基于Cholesky分解的正交匹配追踪算法简化了迭代过程中矩阵求逆计算来快速求得稀疏表示系数，在稀疏编码阶段比正交匹配追踪算法[10]的稀疏编码迭代时间提升了11.37倍，与最新的基于深度学习的SR算法[14]的重建时间相比提升了17.8倍，大大增强了算法的实时性，同时兼顾了重建质量，具有一定的实际应用意义。在各种SR算法中，放大倍数为2时得到的PSNR值见表2。

Table 2 Comparison of PSNR indexes of different SR algorithms reconstruction results表2 不同SR算法重建结果的PSNR值对比 dB

5 结束语

基于自学习和稀疏表示的快速单图像超分辨率算法重建的目标图像纹理细节较好，但同时会伴随一些比较明显的伪影，算法时间复杂度较高，且在线学习的字典仅适用于特定的单幅图像。为克服这些问题，一方面利用Yang等人的字典学习算法和高频残差图的思想，通过外部HR训练图像集生成高频残差字典和低分辨率字典，不仅降低了字典的计算复杂度，更精确地生成超完备字典，且能适用于任意图像；另一方面在图像重建阶段用基于Cholesky分解的正交匹配追踪算法求解稀疏系数，极大地降低了算法复杂度，重建出的目标图像不仅保持了很好的纹理细节，还较好地恢复出尖锐的边缘结构信息。实验结果表明，本文算法具有极高的实时性能，且具有与现有经典超分辨率重建方法相匹配的峰值信噪比。下一步工作是在现有研究的基础上，对字典学习算法和特征提取算法进行改进，以获得更好的重构质量。