中医临床疾病数据多标记分类方法研究*

潘主强，张 林，张 磊，李国正，颜仕星

1.西南石油大学 计算机科学学院，成都 610500

2.中国中医科学院 中医临床基础医学研究所，北京 100700

3.中国中医科学院 中医药数据中心，北京 100700

4.上海金灯台信息科技有限公司，上海 201800

1 引言

在二分类问题和多分类问题中，每个样本只属于一个标记只属于某一个类，可归结为单标记学习问题[1]。但在现实世界中，每个样本可能同时属于多个类别，这是典型的多标记学习问题[2]。并且现实世界中多标记学习任务无处不在[3]，如一个人可能患有多种疾病，风景图片可能包含多种语义类别。这些问题不同于二分类问题和多分类问题，由于类别间的相关性和共现性，使它处理起来比单标记问题要困难得多。因此多标记学习已成为机器学习领域研究热点，并受到了广泛关注[4]。

在已有的多标记学习算法中，多标记k近邻（multi-labelknearest neighbor，ML-kNN）[5]算法是目前常用的一种多标记学习方法，具有较好的性能。但是ML-kNN算法在学习过程中，k是一个预先确定的值，没有考虑样本本身的特点，并且样本类别间存在不均衡问题。在中医临床疾病数据中，这种情况非常普遍，如一个患者可能患有多种疾病，具体到每个疾病而言，疾病类别的数据之间可能存在不均衡的情况。在已有的多标记学习算法中，对于多标记的不均衡研究也较少[6]。而数据挖掘在中医辅助诊断中被日益重视，计算机辅助诊断其实就是数据挖掘分类任务[7]，分类性能的好坏直接影响到辅助诊断的能力。如果能够提高多标记分类的性能，对于提高辅助诊断能力也是非常有帮助的。结合中医临床疾病数据的实际情况，在WML-kNN（weighted multilabelknearest neighbor）的基础上结合权重以及粒计算提出了改进算法——基于粒计算的WML-kNN（weighted multi-label granularknearest neighbor，WMLGkNN)，对中医临床疾病数据进行多标记分类研究。

2 ML-kNN算法和WML-kNN算法

现有多标记学习的分类算法大多数是应用单标记分类算法的思想，比较有代表性的是多标记学习问题转化为若干个独立的二分类学习问题的BR（binary relevance）[8]算法，直接将多标记学习问题转化为多类学习问题[9]的RAkEL（randomk-label sets）算法，周志华等人提出的多标记k近邻（ML-kNN）[5]算法，基于神经网络改进的BP-MLL[10]（back-propagation multi-label learning）算法。在已有的算法中，运用比较多的是ML-kNN算法。

在单标记空间中，k近邻算法的核心是首先寻找出预测样本在训练集中的近邻，然后所有近邻以其本身的类别情况对此预测样本进行投票，那么此样本的类标就与得票多的一方的类标相同。在ML-kNN算法中，首先需要在训练阶段对训练数据集的样本进行统计，通过对训练样本的k近邻进行统计与分析，计算出不同的近邻分布情况下的先验概率和后验概率。对于每个测试样本，首先确定它的k个近邻样本；然后根据k个近邻样本的标记信息，用最大后验概率（maximum a posteriori，MAP）准则预测它的类别标记集合。但是针对中医临床疾病数据，ML-kNN算法有个很大的缺陷：具体到某个标记，数据类别出现不均衡。

在ML-kNN算法中，如果样本中某个类数量过少，致使取到的k个近邻中该类所占的比例较小，易造成错分[11]。在中医临床疾病类别数据中，这种情况比较常见。例如，在中医临床多标记疾病数据中心血管类疾病，患病的个体要少于未患病的个体。如果按照ML-kNN算法进行分类，分类效果不会太好。为了解决多标记数据中存在的类别不均衡问题，张顺等人[11]基于ML-kNN和权重提出了WML-kNN算法（如算法1）。WML-kNN算法的主要思想是：先求得样本的近邻集，根据近邻集的类别情况对样本类别的先验概率进行加权处理，以提高少数类的权重，减少分类的错误率。WML-kNN在一些公开数据集上取得了较好的效果。

算法1WML-kNN算法

输入：训练数据集Sk,近邻集合大小k，测试数据t。

输出：测试数据t的类别标记。

1.对于每一个类别标记，计算其先验概率。

2.计算测试数据t和训练数据集Sk的距离。

3.根据设定的k和距离确定测试数据t的近邻集合Q(x)。

4.计算每一个类别标记的后验概率。

5.对于每一个类别标记重复步骤6、7。

6.根据近邻集合Q(x)和式（2）计算类别标记权重w。

7.对先验概率用w加权，然后用ML-kNN方法确定是否赋予标记l。

8.确保每个标记都得到赋值，结束。

但是WML-kNN和ML-kNN算法都还存在另一个问题，在构建样本的近邻集时大小是一个预先设定的固定值。样本的最近邻个数是每次执行前预先给定的，没有考虑到各个样本点的具体情况。在中医临床数据中，每一个样本（实例）都是一个具体病例。由于个体的特殊性，很可能每个病例所具有的相似病例是不同的（即不同的近邻群体），如果按照每个病例样本构建近邻集时都采用相同的固定值，对于下面两种情况可能会有一个比较差的效果：一是由于某些病人具有一定的特殊性，很可能和他相似的病例不多，采用固定的k值纳入了不相似的病例样本；二是和他相似的病例很多，但是按照固定的k值却没有完全将相似的样本纳入其中。

为了形象描述这两种情况，将这两种情况用图1来表示。图中正方形和圆形均表示样本点。如图1（a）所示，黑色的正方形点和白色正方形点距离较远，相似度较差，具有较大的差异性。但如果此时k取8，黑色的正方形点将会被加入最近邻集。如图1（b）所示，圆形点和白色正方形点距离较近，相似度基本相同。但如果此时k取8，会有圆形点不被加入最近邻集。

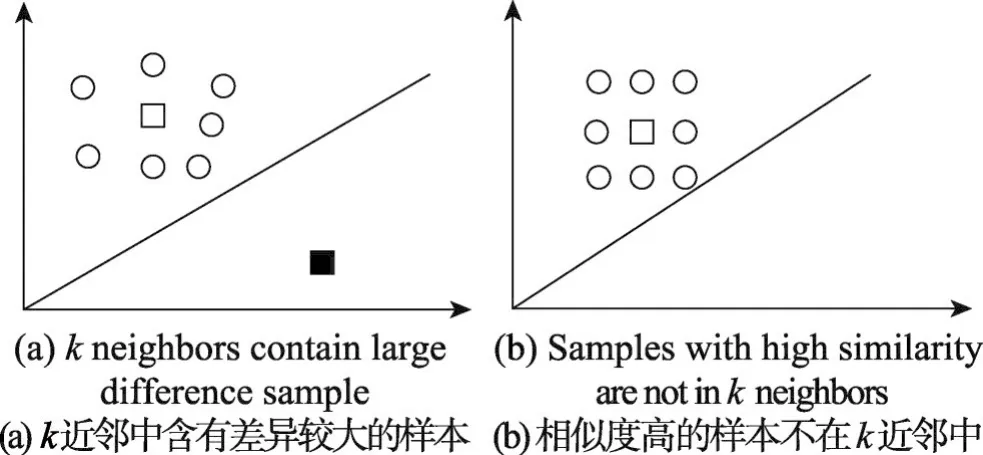
Fig.1 Neighbors are constructed with fixed neighbors图1 采用固定近邻大小构建的近邻

从上述情况来看，采用固定值来构建病例样本的近邻样本集不能充分反映中医临床数据样本分布特点，势必对分类结果有所影响，而且对于k值的选取并没有成熟的指导理论。之前陈小波等人[12]尝试将粒计算的思想融入ML-kNN方法来解决近邻k的取值问题。本文结合中医临床疾病数据的实际情况，基于权重和粒计算在WML-kNN的基础上提出改进算法WML-GkNN来处理中医临床的多标记问题和数据类别的不均衡问题。

3 WML-GkNN算法

根据粒计算的相关理论，多标记学习论域就是所有的样本点。这里需要定义一个等价关系簇来构造不同层次的粒度空间，然后通过这些粒度空间来求解多标记学习问题。设0=e0＜e1＜e2＜…＜em＜…,且当m→+∞ 时em→+∞，则可知E={[ej-1,ej],j=1，2，…}构成了[0，+∞]的一个划分，一个划分可以构成一个等价关系。e(x,y)为论域X上的一种距离，x0为一给定的样本点，定义：

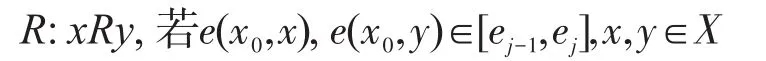
则容易证明R是X上的等价关系，且可以通过j选取的不同来形成不同的等价关系，从而形成论域X上的不同层次粒度空间。具体到ML-kNN算法以及中医临床疾病数据，在构建样本近邻集时，为了选取到与测试样本病例相似性高的近邻病例，设置一个比率property（简写为pro)，通过该值来控制样本近邻点k的个数。对于给定测试样本x，设训练集中与它的距离从小到大的点依次为x1,x2,…,xk,…，相应距离表示dis(x,xj)。

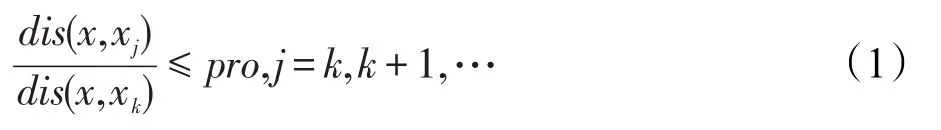
这里选择最近邻集中最后一个样本点q满足式（1）条件，则x1,x2,…,xk,…,xq相互等价。通过pro的取值大小可以控制粒度的粗细，即等价类的大小。这样对于某一给定的样本点，其最近邻样本点的个数以及具体的样本点都可以由pro来确定，而pro既可以通过人工手动设置，也可以通过最优化方法求得。

在WML-GkNN算法中，首先通过粒计算方式求出样本病例最可能的近邻集；其次根据近邻集的类别标记信息对该样本病例类别的先验概率加权，再求出最大后验概率；最后得到测试样例的类别标记。

在WML-GkNN算法中，设Q(x)和|Q(x)|分别表示测试样本的最近邻样本集和最近邻样本集的大小。对于类标集合L中的每一个类计算正例和负例的概率P(po)和P(ne)。对每个类，相应的权重为：

在WML-GkNN算法中，先验概率的计算和ML-kNN算法相同。计算训练集中每个标记的先验概率和

式（3）中，l∈L;s为平滑参数（smoothing parameter），需要预先给定，通常情况下s设置为1，对应Laplace平滑。在引入粒计算的基础上，由于不同的样本近邻集大小不同，对于后验概率的计算略有不同。为了避免混淆，有如下定义：由pro确定的测试样本t的最近邻集大小为st;Elj(st)表示测试样本t的si个最近邻中恰好有j个样本都含有标记l这一事件；b(st)[j]表示训练集样本中自身含有标记l且它的st个近邻同时含有标记l的样本数目；b(st)′[j]表示训练集样本中自身不含有标记l但它的st个近邻同时含有标记l的样本数目。

相应的后验概率为：

测试样本t的类别标记向量Cl和标记隶属度向量Ml为：

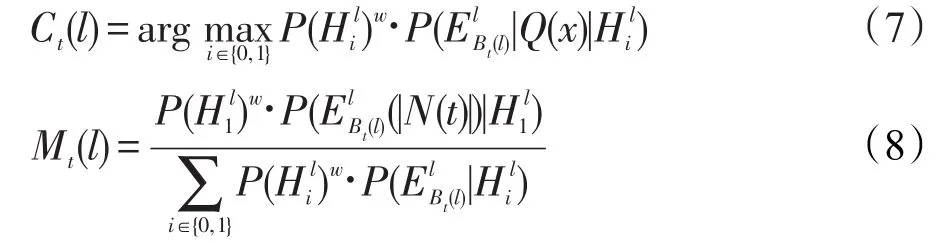
WML-GKNN算法如算法2所示。首先计算各个标记的先验概率，然后计算测试样本t与训练集中样本实例的距离，并按照距离由小到大排序，然后根据pro和式（1）决定最近邻集合Q(x)，为了便于同其他算法比较，Q(x)设定的k值为样本最小近邻集。根据Q(x)和式（2）计算各个类别的权重w，根据权重w对先验概率加权后，用式（7）、（8）计算类别标记向量Cl和类别标记隶属度向量Ml，进而得出测试样本t的类别。

算法2WML-GkNN算法

输入：训练数据集Sk,近邻集合大小k，测试数据t。

输出：测试数据t的类别标记。

1.对于每一个类别标记，计算其先验概率。

2.计算测试数据t和训练数据集Sk的距离。

3.根据设定的k和距离以及pro确定测试数据t的近邻集合Q(x),|Q(x)|≥k。

4.计算每一个类别标记的后验概率。

5.对于每一个类别标记重复步骤6、7。

6.根据近邻集合Q(x)和式（2）计算类别标记权重w。

7.对先验概率用w加权，然后用ML-kNN算法确定是否赋予标记l。

8.确保每个标记都得到赋值，结束。

4 数据集来源与预处理

实验采用临床采集的经络电阻值数据，共3 053例样本。本文选取其中的原穴经络电阻数据，针对睡眠情绪类疾病进行分类研究。数据包含左右各12原穴、性别、身高、体重、年龄等28个特征。

在多标记分类研究方面，根据有效样本数在已有的数据集中本文选择心血管类、血脂病类、尿酸类3类疾病数据。心血管类疾病包含贫血、冠心病、窦性心动过缓、房颤、室性早搏、窦性心律不齐、高乳血症1、慢性心力衰竭等8个小亚型疾病；血脂类疾病包含脂肪肝、血脂代谢紊乱、脂肪肝和血脂代谢紊乱、脂肪肝待排和血脂代谢紊乱、脂肪肝待排等6个小亚型疾病；尿酸类疾病包含高尿酸血症。由于各个疾病在亚型数量上不一致，为了方便进行多标记研究，对疾病下的亚型进行了归并处理，使每种疾病的分类情况为：不患有此类疾病和患有此类疾病两种类型，在数据中分别用0和1表示。用于多标记学习分类研究的数据集中不同疾病分布情况如表1所示，数据的标记分布情况如表2所示。

Table 1 Multi-label data set for disease distribution表1 多标记数据集疾病分布情况

从表1中可以看出，不同疾病患病（阳性）人数和未患病（阴性）人数是不均衡的，阴性样本个体远超过阳性样本个体，且各个疾病的阴性样本数量和阳性样本数量是不同的。同时对患病情况进行统计，结果为：3种病均未患1 310例，患一种疾病689例，患两种疾病195例，患3种疾病20例。

Table 2 Multi-label data set表2 多标记数据集情况

表2中，features表示特征数，labels表示标签的个数，cardinality表示每个样本实例的平均标记数，density是cardinality与标记总数的商值。

5 多标记分类性能评价

多标记学习框架中，每个样本可能同时隶属于多个类别标记。因此与单标记学习系统相比，多标记学习系统的评价准则要更加复杂。到目前为止，已提出了许多多标记学习系统的性能评价准则[13]。本文选取了5种常用的评价准则，即Hamming Loss、One-Error、Ranking Loss、Coverage、Avg Precision 来评价多标记学习系统的性能。假设T={(x1,y1),(x2,y2),…,(xp,yp)}为多标记测试集，并根据预测函数fl(x)，定义一个排序函数rankf(x,l)∈{1,2,…,L} ，如果fl(x)＞fk(x)，则rankf(x,l)＜rankf(x,k)。具体定义如下。

（1）Hamming Loss：该指标用于评估样本的真实标记与系统预测所得标记之间的误差率。

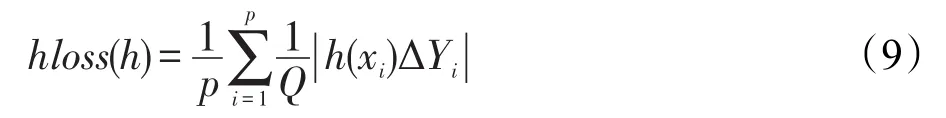
式（9）中，Δ代表集合h(xi)和Yi之间的对称差分，即进行布尔运算中的逻辑异或操作。在算法评价过程中，该指标值越小，表示分类性能越好，当hloss(h)值为0时，其性能最优。

（2）One-Error：该评价指标用于考察在样本的类别标记排序序列中，排名最高的标记不是样本真实标记的可能性，在单标记学习中，演化成一般的分类错误率。one-error(f)越小，性能越好，当one-error(f)值为0时，性能最优。

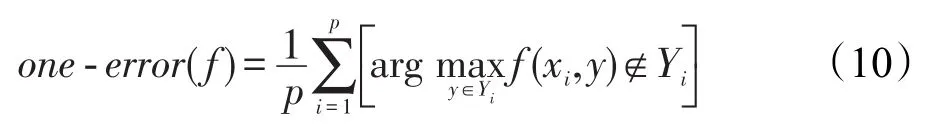
式（10）中，f(，)为与多标记分类器对应的实值函数。

（3）Ranking Loss：计算实例的相关类标排序错误的类标对的数目。rloss(f)越小，性能越好，当rloss(f)为0时，性能最优。

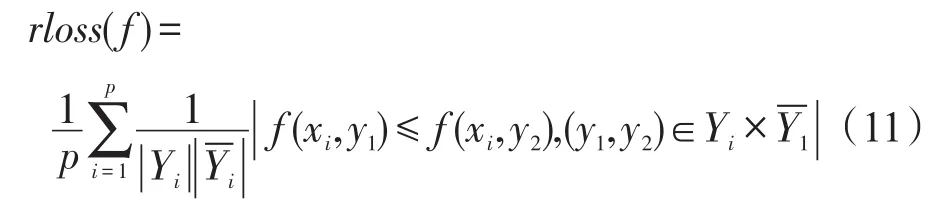
（4）Coverage：评估要在排好序的类标集Y中查找多少步才能把实例xi的类标都找到。coverage(f)越小，性能越好。

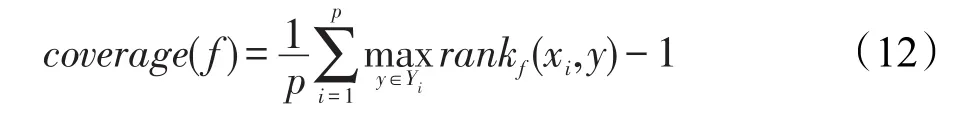
（5）Avg Precision：该评价指标考察了在样本的类别标记排序队列中，隶属度值大的标记仍为其相关标记的情况，即反映了预测类标的平均精确度。avgprec(f)越大，性能越好，当avgprec(f)为1时，性能最优。

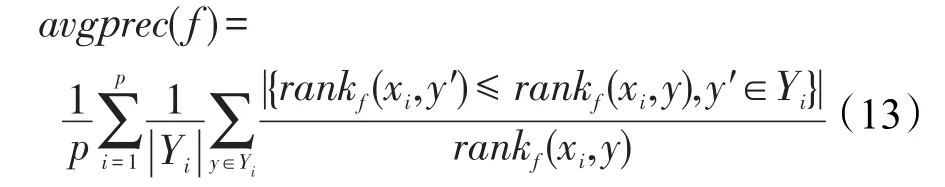
6 实验结果与分析

实验的主要目的是：测试在中医临床数据上运用WML-GkNN算法是否能够提升少数类的分类精度以及优化近邻的选择。相较于已有算法，主要观察WML-GkNN算法是否能够提升Hamming Loss、Avg Precision这两个主要指标。

本文将改进的算法WML-GkNN与ML-kNN、WML-kNN运用于已收集的中医临床数据中，除以上3种算法外，同时使用RAkEL、BP-MLL、BR这3种运用较多的多标记分类算法进行分类与比较。在实验中WML-GkNN算法的pro采用人工设置的方法实现，因为WML-GkNN算法近邻的个数是根据pro以及样本本身情况来确定，而在实验中所设置的k为最小近邻集大小，所以WML-GkNN算法的实验结果并不一定是最优的结果。

分类器参数设置如下：

（1）RAkEL的基分类器为J48，使用默认的参数设置。RAkEL其余参数设置为：k值设为3，Size Of Subset=2，n=2L，L为标记的数量。

（2）ML-kNN中的k设为10，平滑参数设为1。

（3）BP-MLL 中learningRate=0.05，epochs=100，hiddenUnits=0.2。

（4）BR的基分类器为J48，其余使用默认的参数。

（5）WML-kNN中的k设为10，平滑参数设为1。

（6）WML-GkNN中最小的k设为10，平滑参数设为1，pro设为1.05。

所有实验使用十折交叉验证去评估多标记分类相关性能评价，为了排除随机性，每次实验重复10次。RAkEL、ML-kNN、BP-MLL、BR、WML-kNN、WML-GkNN都是基于MULAN[14]实现的。在表3中，最优指标用粗体标注。

从表3中可以发现，与ML-kNN算法相比，WML-kNN算法在Hamming Loss、Avg Precision、Coverage、One-Error上有一定程度的提高；与WML-kNN算法相比，WML-GkNN算法在Hamming Loss、Avg Precision、One-Error上又有一定程度的提升。在RAkEL、BP-MLL、BR、ML-kNN算法中，ML-kNN算法在Hamming Loss、Avg Precision、Coverage上优于其他3种方法，总体性能较好。在Ranking Loss方面，BPMLL算法性能最优。从表中可以发现，WML-GkNN算法在总体性能上最优。

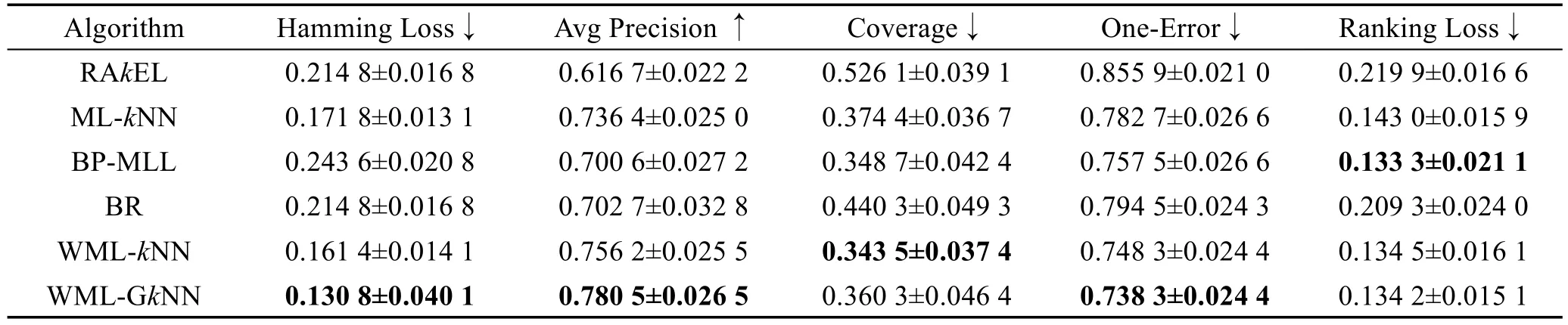
Table 3 Multi-label classification experiment results（Mean±dev）表3 多标记分类实验结果（平均值±标准差）

前面分析过近邻集k的取值大小可能会对相关的方法实验产生影响，那么近邻集k的取值大小会对ML-kNN、WML-kNN算法产生怎样的影响呢，本文继续用实验来探讨。由于所用样本数量为2 214例，如果k取值的范围较小，不能够从整体上反映出相关指标的变化趋势，在此k取值为{1，2，3，5，10，15，20，25，30，35，40，50，60，70}，以探讨随着k取值的增大相应指标的变化趋势。

从图2中可以发现，随着k值的增大，Avg Precision呈现一个先增加后减小而后在局部范围内出现先增后减的振荡变化，由于Avg Precision是越大越好，故随着k值的增大Avg Precision总体结果出现一个下滑的趋势。随着k值的增大，Hamming Loss、Coverage、One-Error、Ranking Loss呈现在小范围内振荡变化但总体上增加的趋势，具体来讲这4个指标呈现出先减小后增加而后在局部范围内出现先减小后增加的振荡变化；当k大于50时，上升的趋势就比较明显。由于这4个指标是越小越好，故随着k值的增大，Hamming Loss、Coverage、One-Error、Ranking Loss结果出现下滑。

从图2中还可以看出，随着k值的增大，相应的评价指标在总体上出现了一个下滑的趋势。正如前面所提到的，样本近邻点个数太大会导致一些与样本相似度不高的点被加入到样本近邻点集中，自然会影响实验结果。在中医临床诊断中，不同病例的相似近邻病例可能是不同的，如果k值取得太大，导致一些与病例样本相似度不高的样本被加入到样本近邻样本集，很可能会对临床数据的疾病分类结果造成影响。

从图3中同时可以发现，pro偏大或者偏小会导致实验评价指标有所下降。还可以发现当pro=1.25时，实验效果最好。究其原因，pro设定是为了在构建病例样本近邻样本集时获取与样本相似度较高的病例样本，当pro取值较大时，会导致一些与病例样本相似度不高的病例样本被放入样本的近邻集中；而当pro取值偏小时，会导致一些与样本相似度较高的点未被放入样本的近邻集中，这些都会导致算法在数据集上进行实验的各项指标下降。

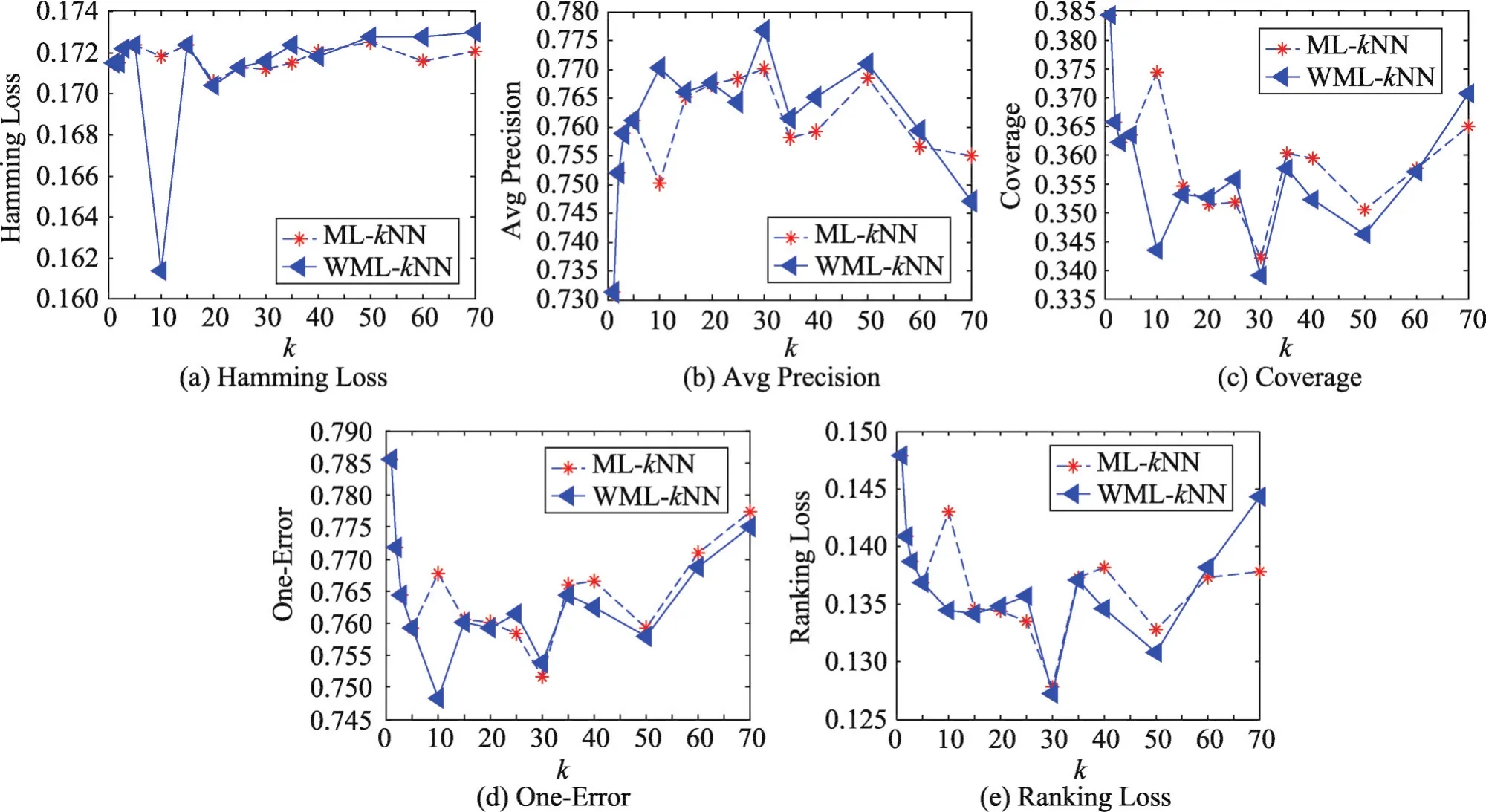
Fig.2 Change trend of results图2 结果变化趋势图

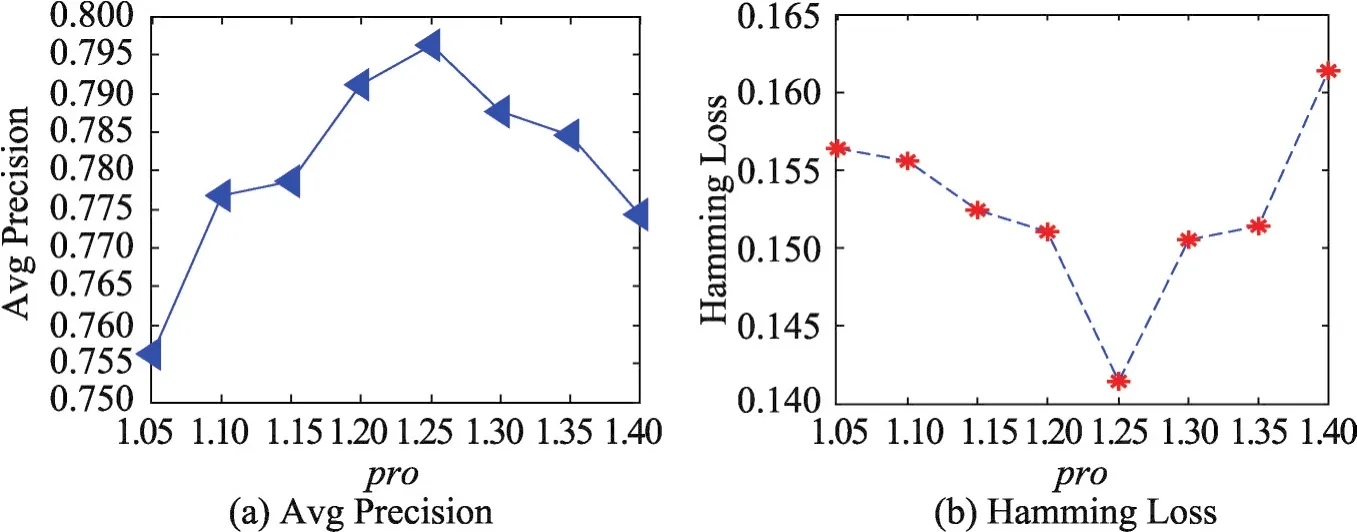
Fig.3 Change trend of results of WML-GkNN图3 WML-GkNN结果变化趋势图

为了进一步比较算法性能，表4给出了在固定最小k值为30的情况下，pro从1.05到1.40各个取值下与ML-kNN、WML-kNN算法固定k值为30的情况下各个评价性能指标。由于标准差较小，表4列出了主要值，未列出标准差，同时相关性能的最优指标加粗标识。

从表4中可以发现，当固定最小k值为30，pro从1.05到1.40情况下，WML-GkNN算法整体优于ML-kNN、WML-kNN算法。除pro最初取值较小时Coverage、Ranking Loss略逊于ML-kNN、WML-kNN算法外，其余的pro取值下相关评价指标均优于ML-kNN、WML-kNN算法。在WML-GkNN算法中，不同的性能评价指标在不同的pro取值下达到最优。pro=1.25时，Hamming Loss、Avg Precision、One-Error取得最优；pro=1.35时，Coverage取得最优；pro=1.30时，Ranking Loss取得最优。从以上对比可以发现，WML-GkNN算法整体性能优于ML-kNN、WML-kNN算法。

在WML-GkNN算法中，通过粒计算尽可能地获得病例的相似样本，通过这些相似样本更能反映样本的实际情况，在此基础上结合权重和ML-kNN，故WML-GkNN算法的分类性能优于WML-kNN算法和ML-kNN算法。同时可以发现，与改进前的WML-kNN算法相比，WML-GkNN算法在Hamming Loss上平均提升11.2%，Avg Precision上平均提升5.3%，Coverage上平均提升2.1%，One-Error上平均提升5.1%，Ranking Loss上平均提升7.6%。就主要评价指标Hamming Loss、Avg Precision而言，WML-GkNN算法性能有较好的提升。

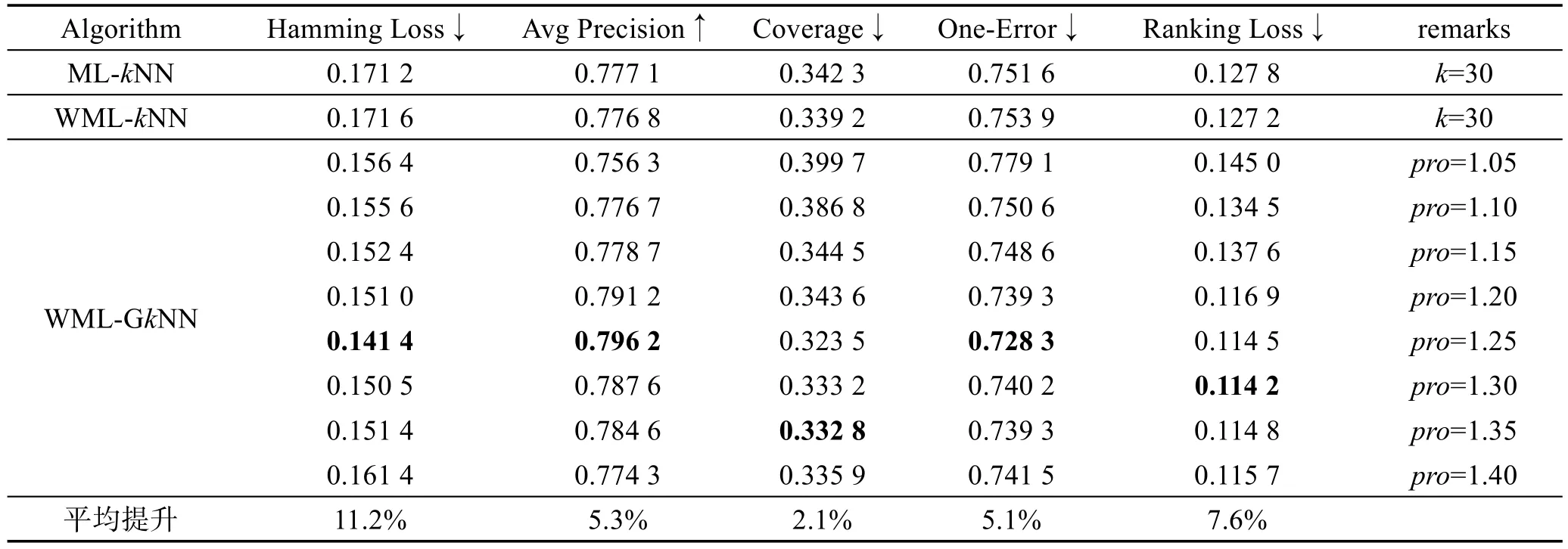
Table 4 Performance comparison of WML-GkNN and ML-kNN,WML-kNN表4 WML-GkNN与ML-kNN、WML-kNN性能比较

为了进一步验证WML-GkNN算法的性能优势，在十折交叉验证的实验过程中，对WML-GkNN和其他比较算法的实验结果进行了配对t校验（pairedt test）[15]，检验P值如表5所示。

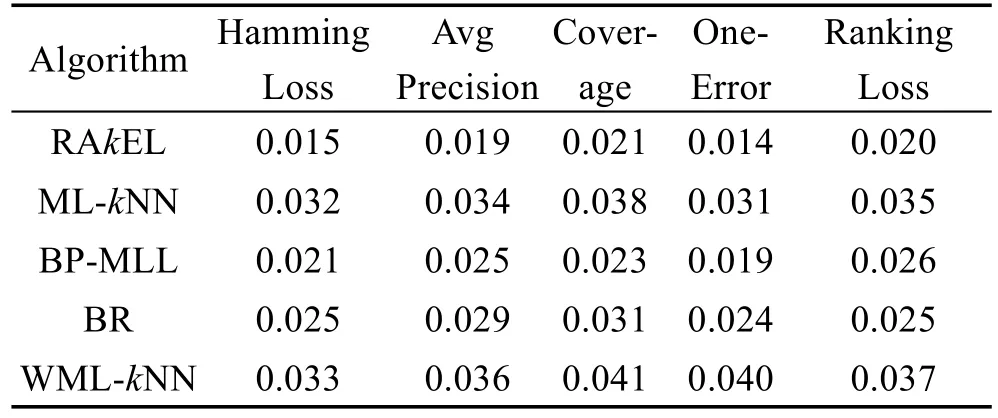
Table 5 P value of t-test of WML-GkNN and other classification algorithms表5 WML-GkNN与其他分类算法配对t检验P值

从表5中可以发现，P值均小于0.05，此分析结果有统计学意义，说明WML-GkNN算法的优势在统计上是可信的，也进一步验证了WML-GkNN算法的性能优势。从已有的几个算法来看，RAkEL算法的P值相对较小，WML-kNN算法的P值相对较大。这说明WML-GkNN算法相对RAkEL而言，具有更好的性能；而针对WML-kNN算法的P值相对较大，这与WML-GkNN算法是在WML-kNN算法基础上进行的改进密切相关。

7 结束语

本文根据中医临床数据的实际情况，结合权重以及粒计算，提出了WML-kNN的改进算法WMLGkNN，针对中医临床疾病数据多标记学习和多标记疾病分类进行了研究。实验表明，与改进前的WML-kNN算法相比，WML-GkNN算法较好地提高了多标记分类性能。但是结合中医临床数据构建样本的粒度空间，以及进一步细化使用权重策略处理多标记数据类别间不均衡问题还需进一步研究。