基于权值相似性的神经网络剪枝*

2018-08-15吕绍和王晓东

计算机与生活 2018年8期

黄聪，常滔，谭虎，吕绍和，王晓东+

1.国防科技大学并行与分布处理重点实验室，长沙 410073

2.武警新疆总队，乌鲁木齐 830063

1 引言

自AlexNet[1]夺得ILSVRC2012年冠军以来，深度学习逐渐兴起，在目标检测[2-4]、语音识别[5]、图像描述生成[6]和机器翻译[7]等多个AI任务中取得极大的进展。这些进展进一步促进深度学习蓬勃发展，从AlexNet到 VGG[6]再到 GoogleNet[7]，趋势是神经网络的层数越来越多，模型规模越来越大，计算量（浮点数）和各项开销也随之上升。表1和表2显示了各个网络应用于具体任务时硬件资源开销和模型运行时长都很大。

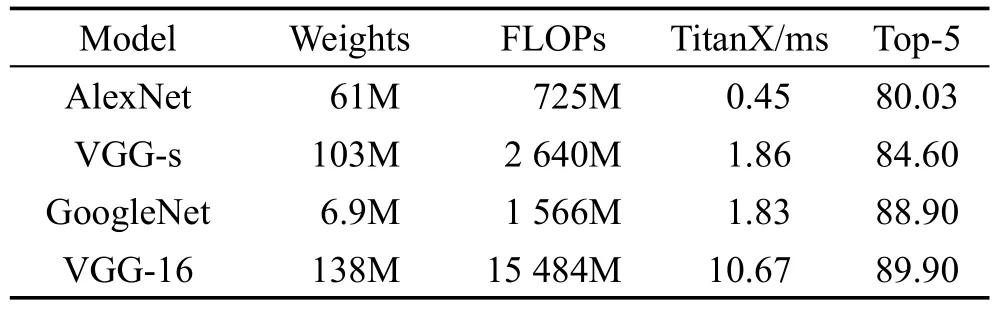
Table 1 Test of several standard networks based on face recognition表1 经典网络在人脸识别任务上的测试

当前网络是重型的，难以应用到实际生活中对智能需求很大，实时性要求高的移动终端[8-9]，因此网络的轻型化逐渐成为人们研究的热点问题。

2 相关工作

深度网络轻型化，即在确保网络性能的前提下尽可能减小网络各项开销，已成为深度学习重要的研究方向。人们或是在已有网络上进行删剪，如最优节点消除（optimal brain damage）[10]与最优节点剪切（optimal brain surgeon）[11]，剪除不重要的权值，二者通过不同方法计算对网络性能影响最小的点；或是希望通过减小计算量对前向传播过程进行加速，比如奇异值分解（singular value decomposition，SVD）方法将权值矩阵分解为向量之间的乘积[12-15]，以减少计算量和参数量；或是针对卷积神经网络（convolutional neural network，CNN）的卷积层做加速，比如FFT方图，这种方法不能减小计算量，但是可以加速计算。有人提出可分卷积的概念，将传统意义上的标准卷积分为深度卷积和点卷积，有效减小了计算量[5,8]。还有专门针对全连接层的压缩方法，如density-diversity[16-18]方法，它提出了density、diversity的概念，density是sparsity的对应词，希望weight尽量多的零；diversity是对quantization而言，希望值尽可能趋同。这种方法可以使得模型易于存储和压缩。

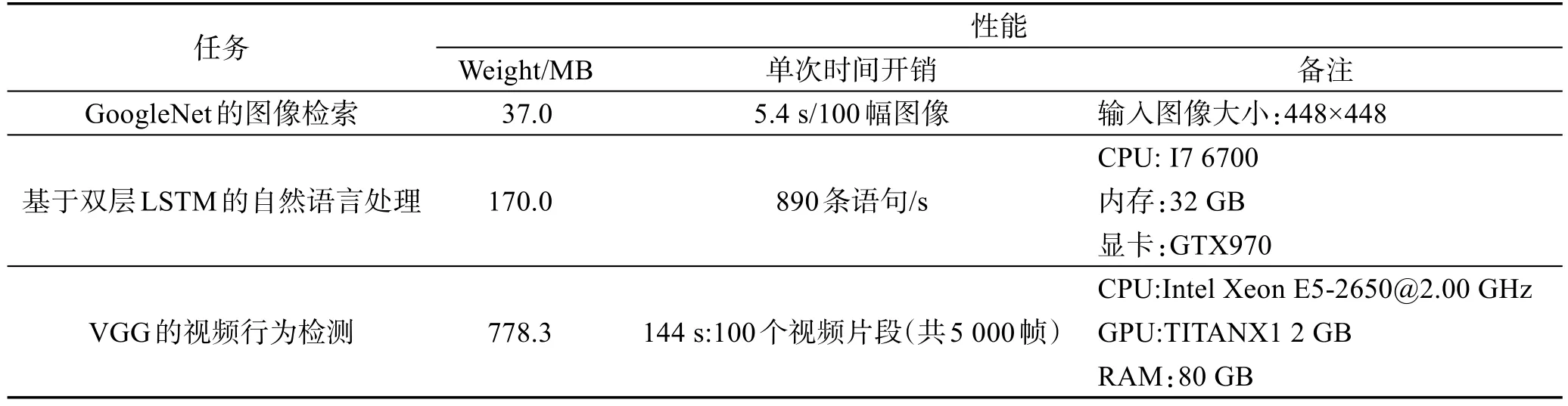
Table 2 Costs of deep neural networks on typical tasks表2 典型任务中深度神经网络的各项开销

除了在原有网络上提出修剪或是加速的方法外，人们还提出了许多新的网络或是新的训练方法，如shallow网络，它的特点是深度小但是很宽，缺点在于难以设计和训练；此外还有人提出二值化网络[19]，将32位浮点数的参数改为二值（-1，+1）表示，从而大大减小网络存储空间；还有工作提出网络训练只训练一部分参数，其余的参数通过已有参数进行“猜测”。还有人进行了对比实验，论证pooling层对神经网络的意义，结论是使用大步长的卷积层取代pooling层得到的网络性能也很好[20]。

本文的思路和贡献如下：考虑到经典神经网络的设计中，计算主要集中在卷积层而参数主要是在全连接层，对卷积层做加速，将可分卷积和卷积层替代采样层的思路结合起来，在原有基础上构建新的网络，探索了可分卷积在深层网络不同卷积层的实际效果，实验表明分段卷积更适用于更深层的卷积层，并且在剪去采样层后运行时间有了明显下降而模型性能保持不变；对全连接层单元做剪枝[21]，主要思想是利用权值矩阵中权值向量之间的相似性合并，剪除全连接层的神经元。还提出了一个超参数α以控制剪枝数目。实验结果表明，本文方法有效减少了运行时间和参数量，能够剪去超过90%的全连接层单元，而模型性能几乎没有下降。

3 方法和理论证明

3.1 卷积层的加速

卷积是神经网络中必不可少的组件，其意义在于提取图像各个层次上的特征，卷积神经网络以卷积命名，可见其重要性。经过发展，现在一个标准卷积通常包括一个卷积层、一个采样层和一个正则化层。

在标准卷积中，输入是多通道的特征图，输出也是多通道的特征图，输出通道数由滤波器的个数决定。设卷积层有K个输入通道和L个输出通道，输入为X，输出为Y，卷积核记为H。卷积核在卷积计算时与输入特征图做滑动窗口的点乘。

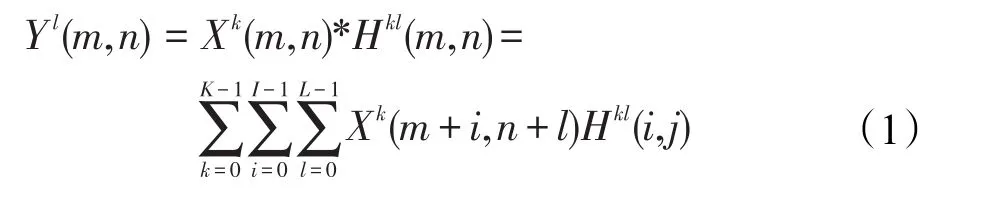
式中，*表示卷积操作。

设输入特征图大小为Gf×Gf，卷积核大小为Gn×Gn，则卷积层每个样本做一次前向传播时的计算量为：

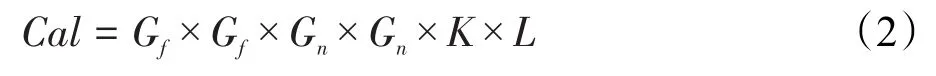
在输入维度保持不变时，若要加速计算，减少计算量，一种行之有效的思路是将标准卷积改为可分卷积，即使用一个深度卷积加一个点卷积来代替标准卷积。因为标准卷积的计算过程其实是包含两个操作：（1）对输入的特征图进行滤波操作（提取特征）；（2）将经过滤波得到的特征图进行组合。这里，深度卷积是对输入的每一张特征图滤波，点卷积则是对滤波结果进行组合。

对深度卷积而言，输入通道为K，卷积深度为D，新的卷积核大小为Gn′×Gn′，则输出通道为K×D；对点卷积而言，输入通道为K×D，输出通道为L，并且满足：

当D=1，卷积步长为1（保持输入输出特征图的大小不变）时，两次卷积操作计算量：

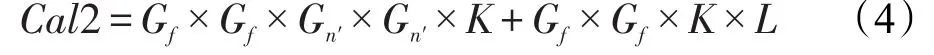
则分解卷积核之后的计算量与分解前的计算量之比为：

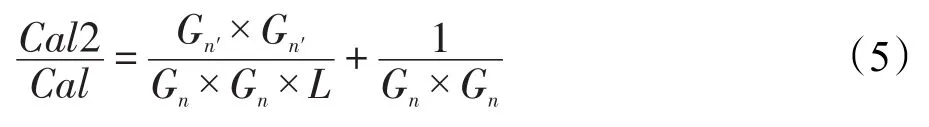
可见，输出通道L较大时，这种方法能有效减小参数量。

3.2 采样层操作

采样层常见于神经网络中，通常构建于卷积层之后，常见采样有平均值采样、极大值采样和极小值采样。设置采样层是出于这样的思路：特征图在经过卷积层后提取了诸多特征，特征量很大，会使得计算十分耗时，而图像的相邻像素点有相关性，间隔几个点取一个点，得到的图片相对于原图片尺寸下降了，计算量大大下降，但是能保留大部分信息。

一直以来都有工作在研究采样层在神经网络中的作用。已被证实的作用包括：对特征图降维，减小计算量；减小提取的特征数，防止过拟合。

研究发现使用全卷积网络也能获得很好的实验性能，卷积输出包含了局部信息，而采样则是直接丢弃了部分信息，二者孰优孰劣难以理论证明[20]，为了减小计算量，现有的Xception、MobileNets等网络已经直接用步长为2的卷积层代替采样层。

在实验中将一个标准卷积（含一个卷积层和一个采样层）改为一个步长为2的深度卷积和一个点卷积。实验显示运算时间明显下降。

3.3 全连接层的剪枝

考虑最简单的全连接层，可以看作是一个带有N个隐含层单元的多层感知机。如图1，输入为X，权值矩阵为[W1,W2,W3,W4]，中间隐含层单元值：

设隐含层到输出的权重为[a1,a2,a3,a4]，激活函数为h，忽略偏置，则输出Z可以表示为：

当W1=W4时，左图可以转换为右图，隐含层单元被去除了，相应输出为：

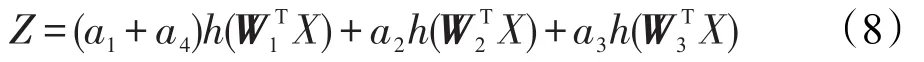
相应地，考虑一般情况，隐含层有n个节点时：

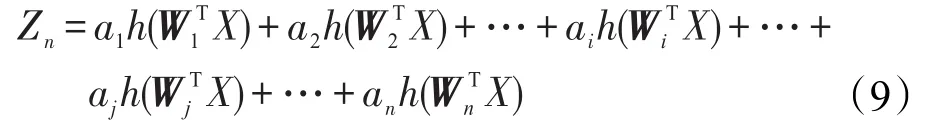
此时假设Wi和Wj相等，可以进行合并，则：

n变为(n-1)，说明中间隐含层单元减少了一个，此时，新的网络参数量和计算量都减少了。

当Wi与Wj相差很小时，可以近似看作是相等，那么如何判定它们的相近程度呢？从结果出发，要求这种权值向量的合并要使得上述两个式子差值最小。由式（9）和式（10）可得：

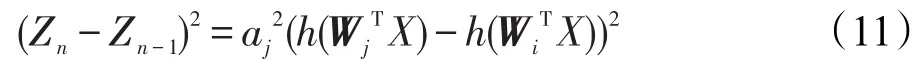
神经网络中常用的激活函数为Relu和Sigmoid，通过推导易知Relu导数值不大于1，而Sigmoid函数导数值不大于1/4，因此：

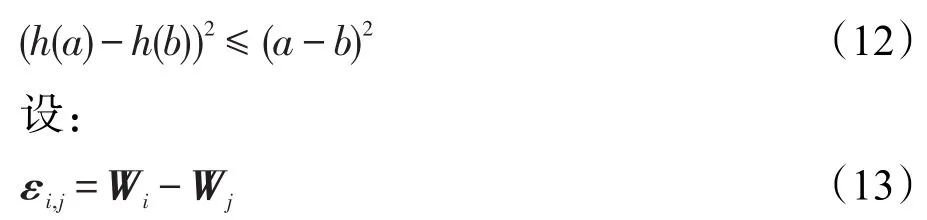
由式（11）～（13）可以得到：

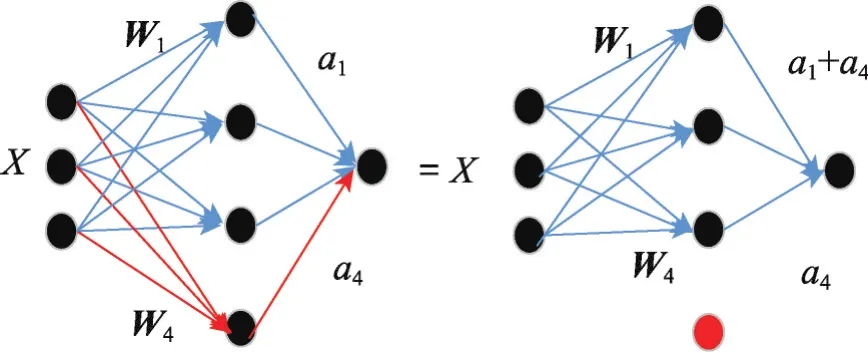
Fig.1 Multi-layer perceptron with a hidden layer图1 带有一个隐含层的多层感知机

根据柯西-施瓦茨不等式，由式（14）得：

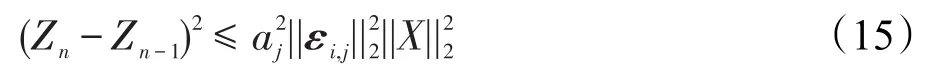
X是输入，和网络结构无关，因此，直接设Si,j用以表示差异程度：

对于十分类问题，最后一个全连接层为10层，那么对于倒数第二个全连接层而言，输出有10个。每个输出单元都有一个差异值矩阵Si,j，针对每个Si,j，选取一个(i,j)对，对每个Si,j，计算Loss，其中K是S矩阵编号，n是S矩阵个数（十分类中为10），而后保留Loss最小的(i,j)对。

3.4 超参数的设定

3.3 节详细叙述了网络剪枝的原理，但是针对一个网络，全连接层单元数是不定的，剪去多少单元合适呢？设定了一个超参数α用以控制网络剪枝的比例1)本节提出了一种超参数用以控制剪枝单元数，需要说明的是，为了使实验结果更加清晰明确，在实验中仅仅对这种全局参数进行了尝试性的使用而非在全部实验组中采用。。

单元合并的基础在于两个权值向量的相似，即：

不考虑X，当i、j位置上的权值向量十分接近时，上式成立。如何度量i、j位置的权值向量接近程度呢？计算两向量的二阶范数平方除以j位置向量的二阶范数，作为度量方式。

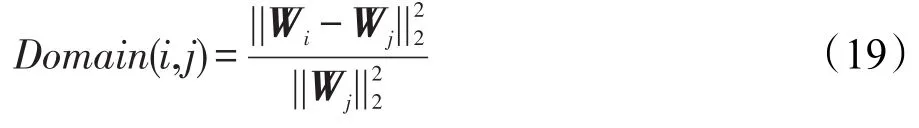
设定超参数α为阈值Domain vaule。完整算法描述如下：

#输入是倒数第二个全连接层的权值矩阵A，A由n个权值向量组成；最后两个全连接层的权值矩阵B，十分类问题中由10个权值向量组成。

4 实验

4.1 实验参数设置

为了使实验具有代表性，采用了标准的mnist手写体数字图片集和cifar10图片集。mnist包含60 000张训练集和10 000张测试集，cifar10是一个经典的彩色图像集，包含60 000张图片共分为10类。

实验所用网络结构如表3和表4所示，来源是tensorflow官网的标准简单卷积神经网络和进阶神经网络。

4.2 实验结果

针对mnist数据集，由于图片尺寸小，内容简单，因此只设计了全连接层的剪枝实验如表5。因篇幅有限表中只列出了部分剪枝结果。

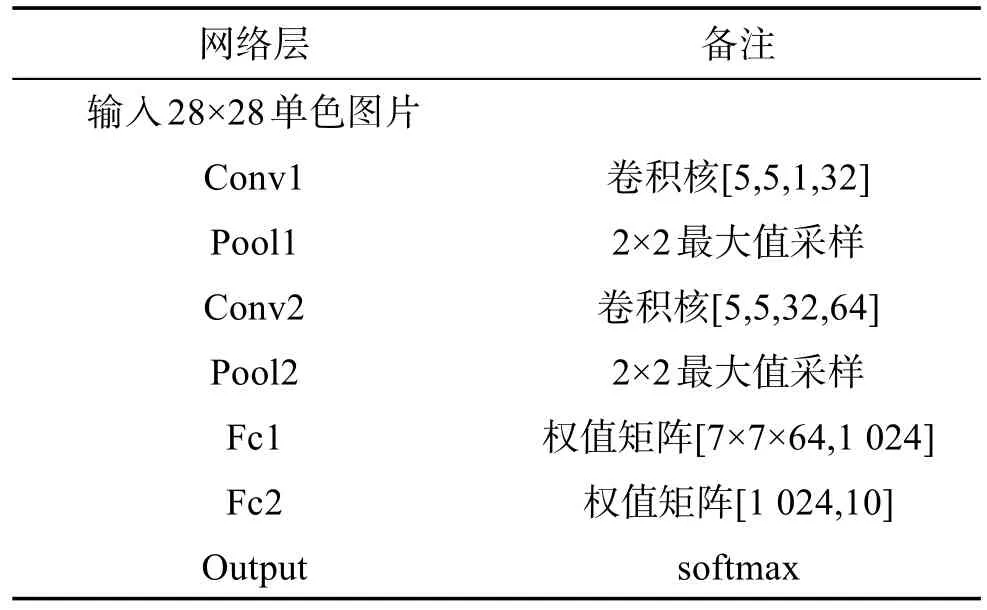
Table 3 Pruning network structure of mnist表3 mnist剪枝网络结构

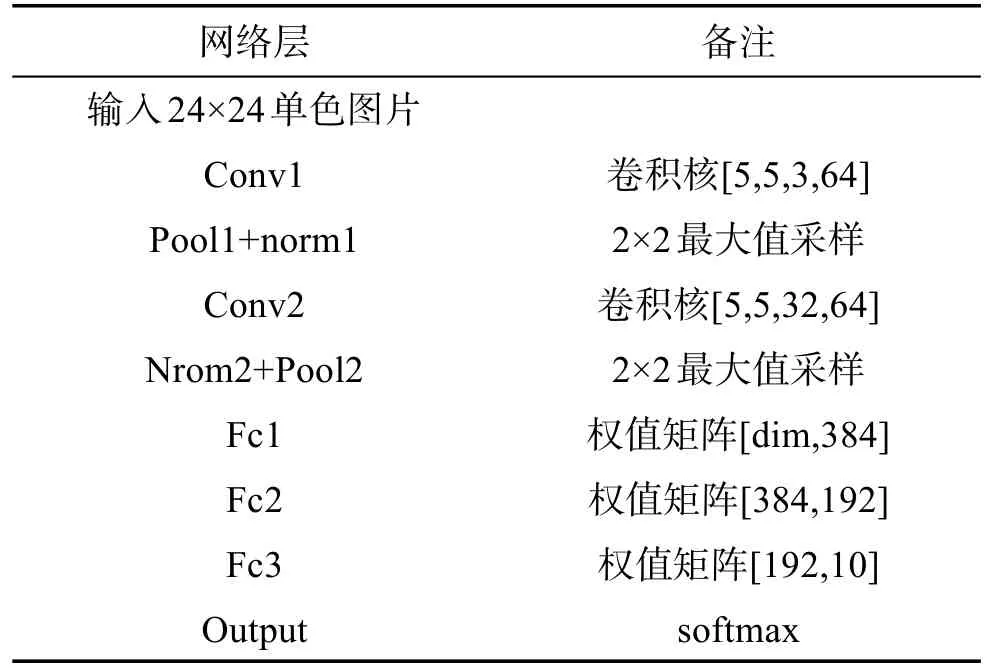
Table 4 Full-connected layer pruning and speeding network structure of cifar10表4 cifar10卷积加速和全连接剪枝网络结构

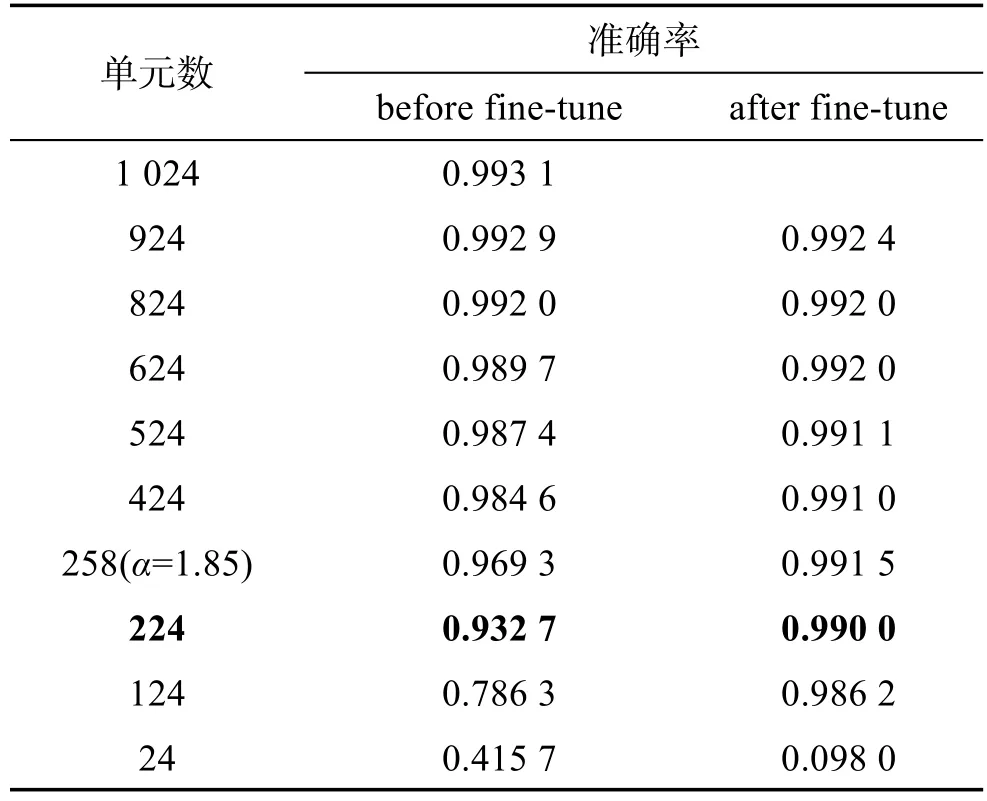
Table 5 Full-connected layer pruning results of mnist表5 mnist网络全连接层剪枝（部分）

从表5中可以看出，在剪去800个单元后，模型fine-tune后仍有99%以上的准确率。在准确率没有明显下降的情况下，通过计算可以得到，参数量减少了76.83%，模型压缩了4.4倍。

针对cifar10数据集，做了大量的对比实验，因篇幅所限仅列出部分结果。表6将原网络结构作如下改动：卷积层改为步长为2的可分卷积，除pooling层；第二列是最后准确率没有明显下降时的剪枝数；第三列是最后准确率；第四列是每次迭代前向运行时间。

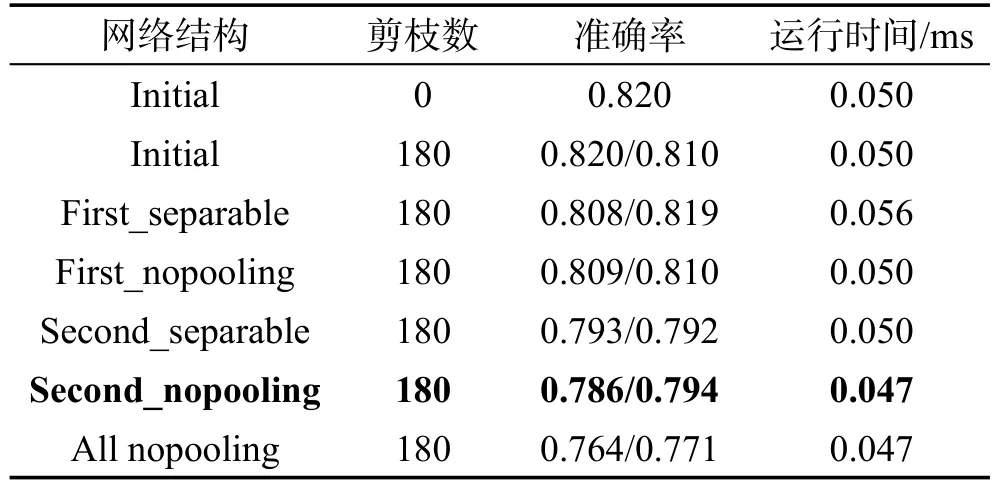
Table 6 Speeding and pruning results of cifar10表6 cifar10网络加速和剪枝实验

从表6可以看到，就cifar10网络结构而言，将第二个卷积层改为可分卷积并去除pooling层时可以有效减小运行时间，缺点是准确率下降较多；将第一个卷积层改为可分卷积时，网络的准确率没有明显下降，模型的运行时间也没有下降（即网络运行消耗没有减小），综合最终准确率和运行时间，将最后一个卷积层分解并去除采样层，而后剪除全连接层192个单元中的180个后取得相对最优的结果。