局部优先的社会网络社区结构检测算法*
2018-08-15李春英汤志康赵剑冬黄泳航
李春英,汤志康+,汤 庸,赵剑冬,黄泳航
1.广东技术师范学院 计算机科学学院,广州 510665
2.华南师范大学 计算机科学学院,广州 510631
1 引言
随着网络技术、智能终端以及计算交流技术的快速发展,社会网络(social network service,SNS)已经成为互联网时代最具影响力的应用。这些以人为中心的社会网络是智能化程度很高的复杂网络,受人的世界观、生活环境、所处位置、兴趣爱好等的影响,其遵循着“物以类聚、人以群分”(社区结构)的特点。而在真实社区结构中,一些用户可能同时属于亲人社区、朋友社区、兴趣爱好社区等多个不同的社区,这样的社区称之为重叠社区。重叠社区检测研究为在线社会网络的推荐系统[1-2]、链接预测[3-4]、异质网络分析[5]、社会网络演变[6]等提供决策性支持,使社会网络在为用户提供优质服务的同时也为其保持用户的粘性和持续活跃度提供了帮助。
社区检测也叫作社区聚簇,近十年已成为计算机、物理、生物、社会学以及复杂性系统科学等多学科的研究热点。学者们从不同角度对社区检测算法进行了尝试,如模块度算法[7-8]、层次聚类算法[9-10]、基于k-clique的算法[11-12]、基于链接聚类的算法[13-14]、基于局部优化和扩展的算法[15]以及基于标签传播的算法(label propagation algorithm,LPA)[16]等。其中,基于标签传播的社区检测算法提出了一个很好的视角,采用信息传播来确定复杂网络中的社区结构。因其简单易行而受到学者的广泛关注。LPA算法采用独一无二的标签对网络中的节点进行初始化,在每一步标签更新中,节点吸收其邻居节点最大的标签。这种基于agent和分散的方法使LPA算法不需要先验知识且拥有近似线性的时间复杂度,因而能够适应于拥有百万级节点的复杂网络[17]。但是LPA算法的异步更新方式导致其具有较弱的健壮性。针对这个问题,文献[18]结合同步更新和异步更新策略,提出LPA算法的半同步更新版本。实验结果表明该算法提高了LPA算法的性能和健壮性。文献[19]综合考虑顶点邻居中相同标签所占比例、顶点度数和边的权重等信息来计算每个顶点的标签影响值并更新顶点的标签。文献[20]提出LPA算法的同步更新版本(synchronous version of LPA,LPA-S)。LPA-S算法使用独一无二的标签对复杂网络中的节点进行初始化,并提出概率更新策略避免在同步更新时产生标签振荡现象。但是,文献[16-20]均是针对复杂网络非重叠社区的检测算法。
实际上,社区重叠是真实复杂网络非常重要的特征,重叠节点在复杂网络中通常扮演着重要的角色[21]。因此,文献[22]提出了多标签同步传播算法(community overlap propagation algorithm,COPRA)检测复杂网络中的重叠社区结构。该算法继承了LPA算法时间复杂度低、适用大型网络等优点。但是其通过输入参数v控制节点所属的社区个数,这难于适应节点所属社区个数差异较大的真实社会网络。另外,一些算法[23-24]的实验结果表明,COPRA算法在一些复杂网络的社区划分结果中存在过拟合现象,即社区划分结果产生了一个包含所有节点的大社区。文献[23]提出了最小极大团标签传播算法(minimal maximal clique label propagation algorithm,MMCLPA)检测复杂网络中的重叠社区结构。该算法采用最小极大团及自适应阈值的方式提高了算法的质量并克服了预先输入参数对未知复杂网络的局限性等问题。但文献[25]在真实社会网络中的实验结果表明MMCLPA算法的自适应阈值偏小,可能导致一些社会网络的社区检测结果中存在过多重叠节点。另外,MMCLPA算法中可能存在同步和异步两种标签更新方式,这可能引起不稳定的社区检测质量。刘世超等[26]提出一种基于标签传播概率的重叠社区发现算法(label-propagation-probability-based,LPPB),LPPB算法根据节点的影响力大小进行更新,综合网络结构的传播特性、节点的属性特征和历史标签记录信息等计算及修正标签的传播概率及更新结果。和COPRA算法一样,LPPB算法通过输入参数调整节点可以拥有的最大标签数,预先输入参数的方法使得LPPB算法很难适应各种类型真实社会网络的社区结构检测。
基于以上研究以及文献[27-28]提出的在微观层次上更加易于检测高质量的社区结构等观点,提出基于微观结构极大团的同步自适应标签传播算法(synchronous adaptive label propagation algorithm,ALPA-S)和异步自适应标签传播算法(asynchronous adaptive label propagation algorithm,ALPA-A)检测社会网络中的社区结构。本文的主要贡献可以概括为两点:(1)两种算法均以微观结构极大团作为社区结构的核心,通过相应更新规则实现节点的标签更新,算法全程不需要参数控制,极大团中节点数和标签权重阈值均会根据网络拓扑结构及节点标签个数的不同而自动调整,使算法能够更好地适应多种拓扑结构类型的社会网络。(2)两种算法均可用于检测社会网络中的重叠社区和非重叠社区,具有良好的适应性。
2 ALPA-S算法
2.1 初始化
k-core[29]是图论中一个非常重要的概念,其被广泛应用于网络结构可视化[30-31],解释社会网络的协同过程[32-33],分析复杂网络中节点的层次和连通性[34]以及分析复杂网络的发展和演化[35]等。在社区检测方面,常常利用k-core作为子路线解决复杂网络中的难题,如计算k-clique、计算连接关系紧密的子图以及求解至少k度子图(at-least-k-subgraph)的问题等[36-37]。考虑到社会网络中影响力大的节点对社区的形成具有一定的促进作用以及基于微观角度更加易于检测社区结构等问题,提出基于网络拓扑结构度量节点的影响力,并按照节点影响力强弱在社会网络中依次寻找局部极大团(如定义1),并为极大团中的节点赋予标签及权重。
定义1(极大团)社会网络被模型化为图G={V,E}的形式,其中V表示社会网络节点集合,E表示节点间相邻关系集合。每个节点vi(vi∈V)都有一个标签集合Ci,N(vi)是节点vi的邻居节点集合,|N(vi)|代表节点vi的影响力。以V中Ci=的影响力最大节点vi及N(vi)中标签集为空的影响力最大节点vj构成的边(vi,vj)为初始边,按照节点影响力强弱构建完全图Gm,称Gm为团。若Gm⊆G,且不存在完全图Gt⊆G,使得Gm⊂Gt,则称Gm为极大团(maximal clique),简称MC。
按照定义1,一个极大团至少包含3个节点。实际上,文献[25]已经表明3个节点可以构成一个小型社区。同时,为了降低算法的运行时间以及避免类似CPM算法[11]在稠密复杂网络中寻找全部极大团耗费大量时间等问题,提出的极大团在复杂网络中是唯一的,即任何两个极大团间的交集为空集。结合定义1,ALPA-S算法标签初始化过程如下所示。
(1)对于社会网络中的任一节点vi的标签集Ci,设置Ci←∅ ;
(2)c←1;
(3)按照定义1寻找MC,对MC中的每一个节点vi的标签集Ci,令Ci←{(c,1)};
(4)c←c+1;
(5)重复步骤(3)、(4),直到没有满足要求的节点为止。
按照算法初始化规则,ALPA-S算法在图1所示的复杂网络中共找到2个极大团,分别为(a,b,c)和(e,g,f)。并且极大团(a,b,c)中节点标签和权重均为1;极大团(e,g,f)中的节点标签均为2,权重也均为1。如图1所示。初始化后MC中的节点均拥有了标签和权重,而非MC节点则没有获得标签和权重。根据复杂网络小世界模型,只要节点拥有邻居,则在算法标签更新中可使其获得标签。
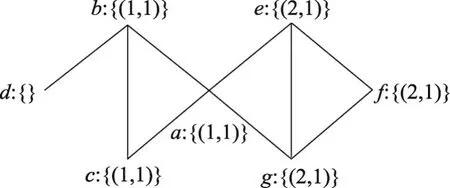
Fig.1 Complex network initialized graph图1 复杂网络初始化结果图
2.2 迭代过程
复杂网络初始化后,一些节点获得了标签和权重,这些标签和权重成为算法迭代开始时的种子。算法迭代时,节点继承其所有邻居节点的标签及按照权重更新规则产生的权重值。通过对复杂网络拓扑结构及节点所属社区情况的深度分析可知,节点是否属于某个社区与节点在该社区对应标签下的权重有关,而节点在某个标签下的权重值则与节点在该标签下的度数分布情况有关。例如,复杂网络中的一个5度节点vi,其中4度贡献给了社区1,说明在vi的5个关系中与社区1中的节点有4条连接关系;1度贡献给了社区2,说明vi的5个关系中与社区2中的节点有1条连接关系。直观上讲,该节点vi应该更大程度上属于社区1,而不属于社区2。因此,标签权重的计算方法需要充分考虑节点度数在各个标签下的分布并且要避免某个邻居节点标签权重过大产生的“吞噬”问题。根据以上分析,提出权重计算公式(1)。假设函数bt(c,vi)表示在第t轮迭代时标签c在节点vi下的权重值。在ALPA-S算法中,权重的更新方法如式(1)所示。
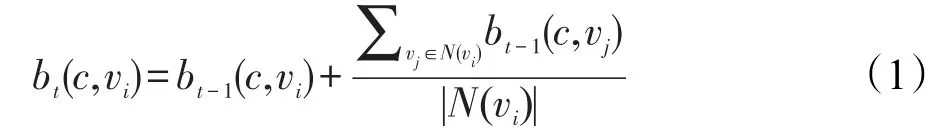
其中,N(vi)表示节点vi所有邻居节点的集合。节点vi在第t-1步已经拥有标签c,则节点vi在第t步更新时,如果其邻居节点vj也拥有标签c,则节点vi在第t步标签c下的权重值为其在第t-1步标签c的权重值与其邻居节点vj在第t-1步标签c的权重值与节点vi度数的比值之和。若被更新节点vi中第t步没有邻居节点的标签c,则bt-1(c,vi)值为0。节点vi接收邻居节点的标签c作为新标签,并按照式(1)计算标签c对应的权重。
另外,考虑到社区结构的局部性以及为了避免无效标签被传播得更远,ALPA-S算法在每次迭代后对所有节点下的标签进行处理。COPRA算法将预先输入参数v的倒数作为节点标签是否有意义的判断阈值。与参数v并不一定适用于社会网络中所有节点一样,将作为所有节点标签权重是否有意义的判断阈值也不一定合适。受COPRA算法的启发,将作为节点标签是否有意义的判断条件。与COPRA算法不同的是是一个与每个节点的标签个数L有关的变量,把这个变量叫作自适应阈值,具体如定义2所示。
定义2(自适应阈值)如果一个节点vi拥有L个标签,则每个有意义标签的权重值应该大于等于即为节点vi对应的权重阈值。每个节点在每次迭代后拥有的标签个数不同,权重阈值因此也不同。把随着节点标签个数发生变化的变量叫作自适应阈值。
ALPA-S算法迭代过程如下所示。
(1)t←1。
(2)按照式(1)更新节点的标签及权重。
(4)归一化所保留节点的标签权重,使其和为1。
(5)如果每个节点都拥有了标签,则算法停止。
(6)否则t←t+1,重复步骤(2)~(5)。
按照算法的迭代规则,对图1复杂网络初始化结果进行第1轮迭代后,节点标签权重的一种更新结果为同时,按照自适应阈值剔除无意义的标签及权重。具体过程为:仅有一个标签的节点不作处理,包含2个及以上标签的节点为e、g、f、a。其中,节点e有两个标签,因此对应的自适应阈值为,删除标签权重小于的标签权重有序对,则节点e仅剩下标签2,为其余3个节点g、f、a与节点e自适应阈值相同,使用类似的方法删除权重小于的标签权重有序对,结果为最后对所有节点的标签权重归一化处理,结果为图2显示了ALPAS算法按照标签更新规则迭代1次后并进行归一化处理后的结果。
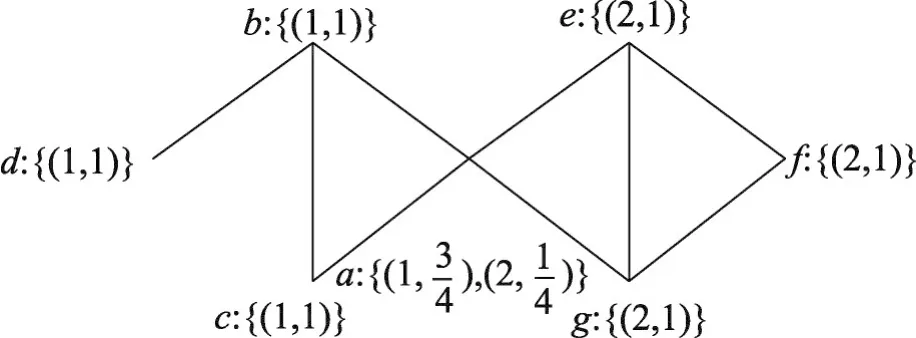
Fig.2 Propagation of labels:first iteration图2 第1次标签传播后的复杂网络结果图
2.3 终止条件
考虑到社区结构的局部性以及离极大团较远的节点拥有标签即达到了局部社区划分的目的,使用所有节点拥有标签作为ALPA-S算法迭代终止的条件。这个终止条件可以使标签在有意义的局部范围内传播并有效减少算法的迭代次数,同时可以避免同步更新算法(如DLPA[38])为了达到稳定状态而产生的标签振荡问题以及过拟合现象等。按照这个终止条件,图1所示复杂网络在第1次迭代后,所有节点都拥有了标签,则ALPA-S算法终止。
2.4 后期处理
在ALPA-S算法中,标签的数量是复杂网络中不相交极大团的数量。随着迭代过程的推进,标签数量逐渐减少。当算法终止时,剩余标签的数量代表复杂网络中的社区个数,一个标签代表一个社区。如果一个节点拥有至少两个标签(即标签集长度|Ci|>1),表明该节点同时属于至少两个社区,则该节点为重叠节点,如定义3所示。按照此规则,图2所示的迭代结果包含两个社区:社区1{a,b,c,d}和社区2{a,e,f,g},则a为重叠节点。但是,按照这种方法形成的社区往往会存在一些子集社区。如在社区结果中有两个不同的社区Ci和Cj,分别为Ci={v1,v2,v3,v4},Cj={v1,v2,v3,v4,v5}。不难看出社区Ci是社区Cj的子集。显然,保留社区Cj更有意义。因此,ALPA-S算法按照定义4的规则处理社区检测结果中的子集社区。
定义3(重叠节点)Ci和Cj是两个不同的社区,若节点vi同时属于社区Ci和Cj,则称节点vi为重叠节点。即:overlap(vi)⇔∃vi(vi∈Ci∩Cj∧Ci≠Cj)。
定义4(社区处理)若存在社区Ci和并且Ci⊆Cj,则删除社区Ci,保留社区Cj。
2.5 时间复杂度
假设复杂网络中有n个节点且节点的平均度数为k,有H个极大团且极大团平均节点数为m。ALPAS算法的时间复杂度主要分为三部分:(1)初始化过程;(2)迭代过程;(3)后期处理。
ALPA-S算法在初始化阶段设置网络中节点vi的标签集Ci=Φ,时间复杂度为O(n);之后按照定义1寻找网络中的MC,寻找MC过程产生的时间复杂度为因此,ALPA-S算法整个初始化过程产生的时间复杂度为
假设ALPA-S算法收敛时需要的迭代次数为T,每个节点更新标签分为3个过程:
(1)按照式(1)更新当前节点的标签及权重;
(2)对更新后的节点标签进行处理;
(3)对节点保留标签的权重进行归一化处理。
因此,ALPA-S算法迭代过程的时间复杂度为O(Tkn)。
ALPA-S算法后期处理过程产生的时间复杂度为O(n)。
3 ALPA-A算法
考虑使用异步标签传播方式会使算法更快收敛,提出异步自适应标签传播算法(asynchronous adaptive label propagation algorithm,ALPA-A)。ALPAA算法的初始化过程、后期处理过程与ALPA-S算法相同。不同之处在于ALPA-A算法采用异步更新方式,具体更新规则如式(2)所示。
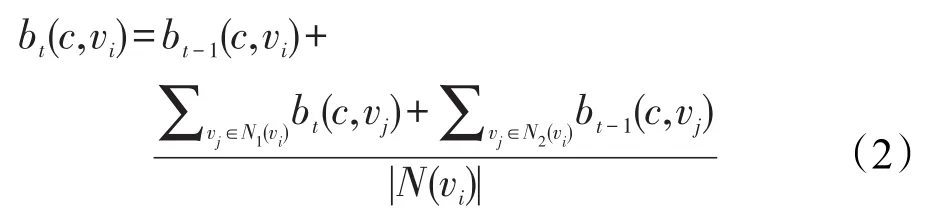
其中,bt-1(c,vi)为节点vi在第t-1步被更新的结果。N(vi)为节点vi的邻居节点集合,N(vi)=N1(vi)∪N2(vi),且N1(vi)∩N2(vi)=∅。N1(vi)中的节点在第t步已经被更新,N2(vi)中节点的最新结果则是在第t-1步被更新。如果节点vi的邻接节点vj在第t步被更新,则更新节点vi的标签及权重时使用节点vj最近被更新的结果。否则使用其在第t-1步的更新结果。ALPAA与ALPA-S只是算法迭代过程采用的更新规则不同。尽管两种算法收敛时的迭代次数可能不同,但它们的时间复杂度是一致的。
4 实验
4.1 实验数据和评价方法
通过两种方式评估算法的性能:一种是使用仿真网络生成程序LFR[39]生成带有重叠社区和非重叠社区的仿真网络数据集;另一种是使用现实生活中真实的社会网络数据集。实验环境为Win 7 OS、Intel®Core™ i5 3.20 GHz处理器,算法实现为Python2.7程序设计语言,算法评价环境为Eclipse平台下的Java语言,数据集格式均为文本文档。
4.1.1 仿真网络数据和评价方法
LFR仿真网络生成程序在产生仿真网络数据的同时也产生了社区划分的结果,方便算法使用其生成的仿真网络数据集进行社区划分的结果与已知社区进行对比。利用LFR产生的仿真网络数据集如表1所示。其中,n表示仿真网络中的节点数,k是仿真网络节点的平均度数。kmax表示仿真网络中节点度数的最大值。Cmin表示仿真网络社区长度的最小值。Cmax表示仿真网络社区长度的最大值。On表示仿真网络中重叠节点的个数。Om表示仿真网络中重叠节点所属的社区个数。t1为仿真网络节点度数的密率分布指数。t2为仿真网络社区大小的密率分布指数。混合参数μ取值范围是[0,1]。取值越大,生成的仿真网络社区结构越不明显,当取值为0时,整个网络是一个社区;当取值为1时,则生成的是一个随机网络。实际上,真实社会网络大多具有一定的社区结构性,因此本实验使用的仿真网络数据集μ取值范围是[0,0.8],每次增加0.1。

Table 1 LFR benchmark network dataset表1 LFR基准网络数据集
本文使用Lancichinetti等人在文献[40]中提出的标准互信息(normalized mutual information,NMI)评估算法在仿真网络数据集上的社区检测质量。NMI可以测量两个社区间的相似程度,NMI∈[0,1],其值越大表明两个社区越相似。NMI具体信息详见式(3)。
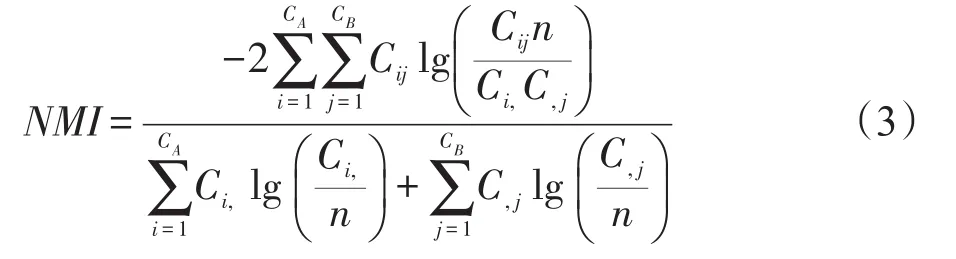
其中,A和B表示网络的两种划分结果,C表示混合矩阵,其元素Cij表示划分A中的社团i里面的节点在划分B中的社团j里面出现的个数。CA和CB表示划分A和划分B中的社团的个数,Ci,表示矩阵C中第i行的元素之和,C,j表示矩阵C中第j列的元素之和,n表示网络的节点个数。
4.1.2 真实网络数据和评价方法
考虑到真实社会网络和仿真网络的拓扑结构等信息存在一定的差异性,使用5种不同规模的真实社会网络(Karate[41]、Dolphins[42]、Football[43]、Power[44]和 CA-hepPH[45])对社区检测算法进行性能评价。Karate[41]是圣所迦利的空手道俱乐部的人际关系社会网络,该网络具有34个节点和78条边,是一个小规模的真实社会网络。Dolphins[42]是Lusseau等[46]在新西兰对62只宽吻海豚的生活习性进行了长时间的观察,发现海豚的交往呈现出特定的模式,并构造了包含62个节点的海豚社会网络。Football[43]是美国大学秋季比赛中各足球俱乐部通过比赛关系产生的社会网络。Power[44]是美国西部电网构成的复杂网络。CA-hepPH[45]是一个科学家合作的较大规模的真实社会网络,具有11 204个节点和117 649条单向边。这些社会网络(如表2所示)中的节点代表的是真实个体,而边代表了个体之间的关系。它们的规模、拓扑结构等特性不同,应该能够更好地评价社区检测算法的性能。
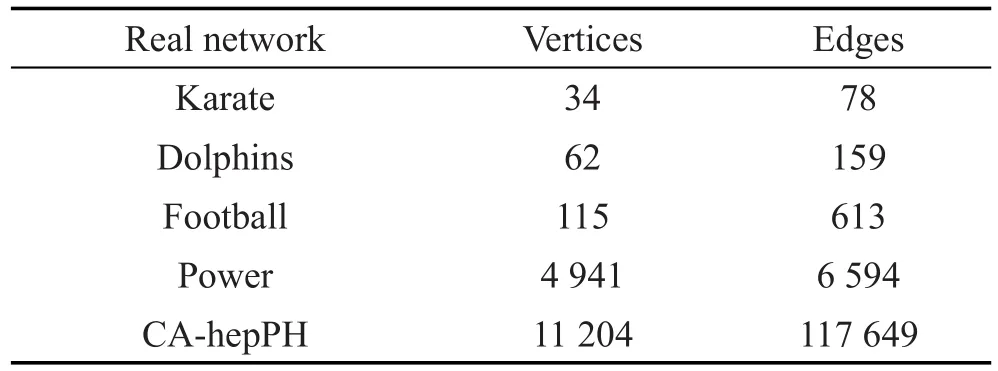
Table 2 Real social network dataset表2 真实社会网络数据集
人们通常不了解真实社会网络的社区结构情况,也很难有事实上的评价标准。Newman等提出的模块度[47-49]方法得到广泛认可并被用于评价社区检测算法在真实社会网络数据集上的社区检测质量。其中,文献[49]将问题扩展到无向无权重复杂网络,提出一个用于检测重叠社区的模块度函数Qov,详见式(4)所示。
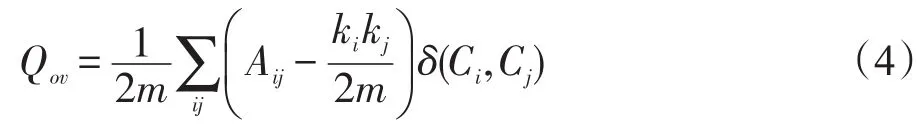
在式(4)中,m表示复杂网络的边数。ki、kj是节点i、j的度数。A是网络的邻接矩阵,如果节点i和j相邻,则Aij=1,否则Aij=0。如果节点i和j在同一个社区,δ(Ci,Cj)=1,否则δ(Ci,Cj)=0。
4.2 算法性能
GCE算法[50]提出k-clique中的参数k为3或4时,clique的大小是比较恰当的。因此,本节对MC的长度进行了限定,分别为|MC|≥3和|MC|≥4两种情况,并使用ALPA-S算法验证两种情况下的社区检测质量。ALPA-S算法分别在S1、S2、S3和S4仿真网络数据集对应的32个仿真网络上运行10次,并对社区检测结果的NMI值进行了平均计算,结果如图3(a)~图3(d)所示,其中图3(a)为仿真网络数据集S1上的结果,图3(b)为仿真网络数据集S2上的结果,图3(c)为仿真网络数据集S3上的结果,图3(d)为仿真网络数据集S4上的结果。
图3表示ALPA-S算法在两种MC长度下在仿真网络S1(a)、S2(b)、S3(c)和S4(d)上的社区检测质量。实验结果表明,当μ>0.5且|MC|≥4时,在小型仿真网络数据集S1和S2上,ALPA-S算法没有取得较好的社区检测质量。而在较大的仿真网络数据集S3上,ALPA-S算法在两种长度的MC上均取得了较好的社区检测质量。但在S4数据集上,当|MC|≥4时,ALPA-S算法的社区检测质量明显劣于|MC|≥3时。实际上,当|MC|≥4时,仅仅包含3个节点的小型社区无法被正确检测,而文献[25]证实过一个真实社会网络的社区可能只包含3个节点。综合考虑,选择|MC|≥3作为ALPA-S算法和ALPA-A算法初始化时极大团长度的限定条件。
另外,ALPA-S和ALPA-A在仿真网络中检测的极大团个数即是两种算法初始化时产生的标签数,为了证明这种方法极大地降低了算法中的冗余标签数以及减少了算法更新时标签选择的代价,现以ALPA-S算法为例,使用表1中较大的仿真网络数据集S3和S4对应的16个仿真网络作为实验数据集验证ALPA-S算法中产生的标签数以及标签节点比,实验结果如图4中的(a)和(b)所示。其中,标签节点比如式(5)所示。在式(5)中,Cn表示仿真网络在ALPAS算法初始化时产生的标签数c与该仿真网络节点数n的比值,即标签节点比。

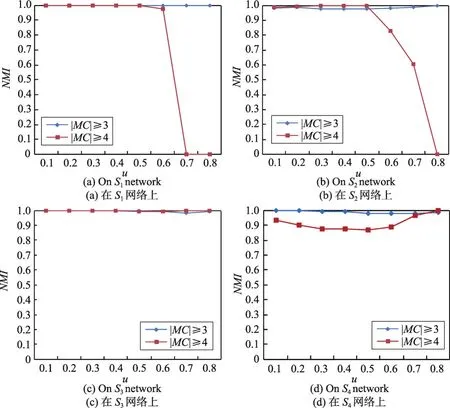
Fig.3 Community detection result ofALPA-S algorithm in both MC lengths图3 ALPA-S算法在两种MC长度下的社区检测质量
在图4的(a)和(b)中,ALPA-S算法在每个仿真网络数据集上进行了10次实验,产生的标签数量略有差异。对10次实验产生的极大团数求平均值。从图4(a)、(b)中可以看出,ALPA-S算法在16个仿真网络上产生的标签节点比(label-node ratio)均小于10%,这极大降低了ALPA-S算法迭代时标签选择的风险,算法结果相对更稳定。另外,这里应该被提及的是ALPA-S算法和ALPA-A算法在寻找极大团时,当有两个或更多个影响力相同的邻接节点同时符合条件加入一个极大团时,算法随机选择其中一个节点。这种随机选择可能导致社区划分质量的差异。但是,通过实验结果分析得知,这种随机选择引起的社区划分质量不稳定性误差范围在0.1%左右。可见,这种随机选择并未引起两种算法社区检测质量的较大不稳定性。被随机选择加入极大团忽略的节点可能最终都没有被加入到任何一个极大团中,但在后续的标签更新过程中,其仍然会和与它有最多关联关系的极大团中的节点拥有同一个标签,并进而属于同一个社区。因此,构建极大团时的节点随机性选择问题对两种算法社区检测质量的影响较小。
使用表1的S5数据集验证ALPA-S和ALPA-A两种算法在具有不同重叠社区数的仿真网络中的社区检测质量,结果如图5所示。从图5可知,当Om=0时,即仿真网络中没有重叠社区时,两种算法均取得了较好的社区检测质量。说明两种算法均适合于具有非重叠社区结构的复杂网络。随着网络中节点所属的重叠社区数目的增加,两种算法均保持着良好的社区检测质量,说明两种算法亦均适合于节点属于多个重叠社区的复杂网络上的社区检测。但是从图5显示的结果可以看出,在5种仿真网络数据集上,同步算法ALPA-S的社区检测质量略优于异步算法ALPA-A。
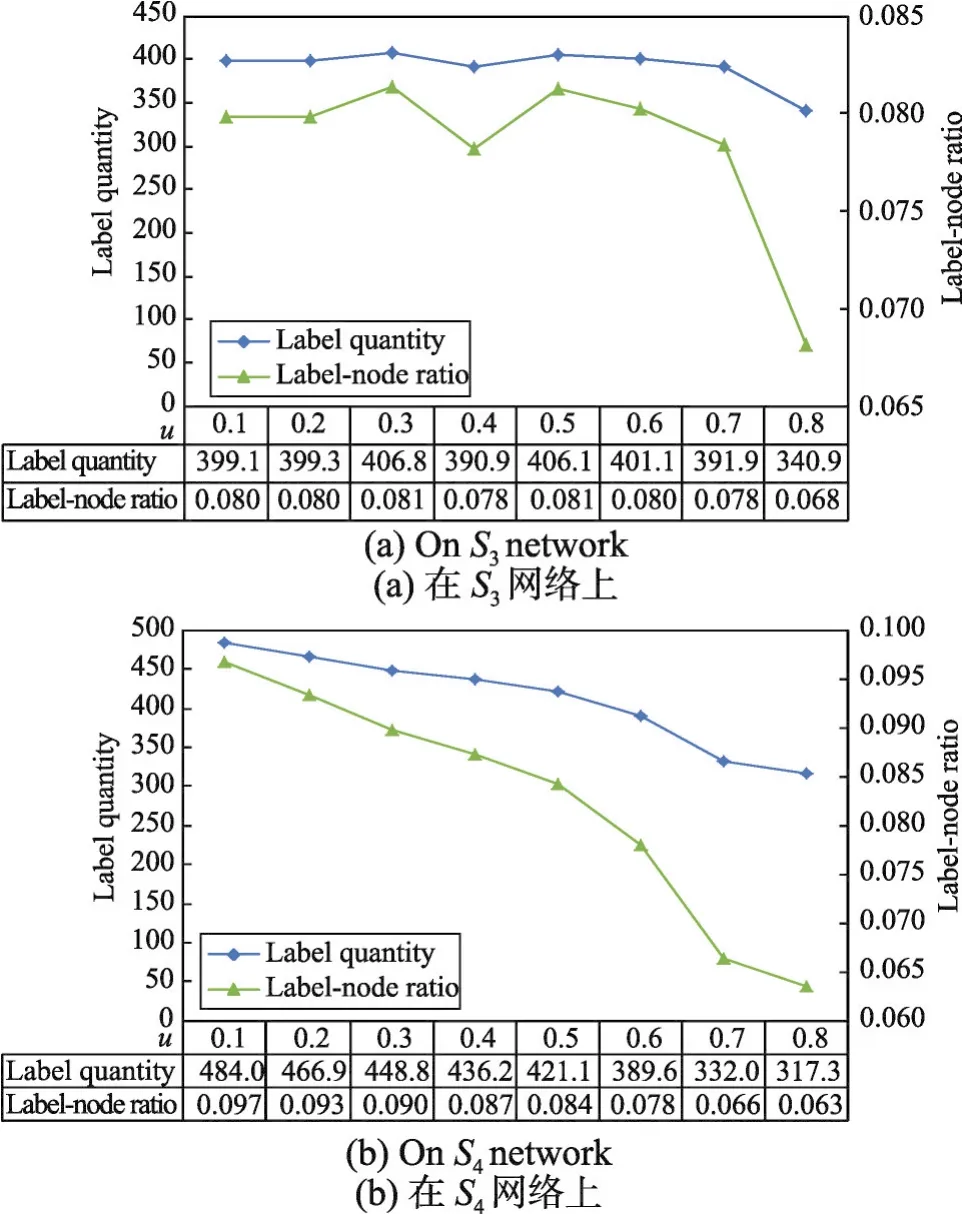
Fig.4 Number of labels and label-node ratio ofALPA-S algorithm on artificial networks图4 ALPA-S算法在仿真网络上产生的标签数及标签节点比
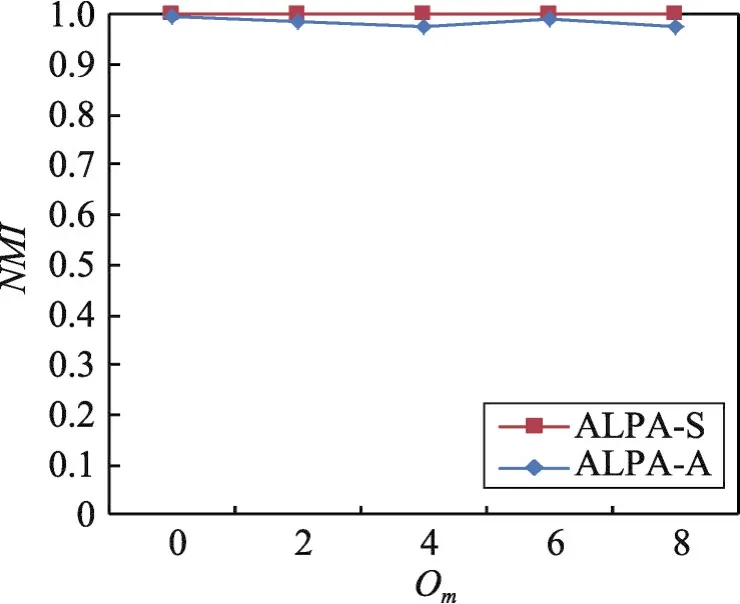
Fig.5 Result of community detection of two kinds of algorithms on artificial networks containing different number of overlapping community图5 两种算法在具有不同重叠社区数的仿真网络上的社区检测质量
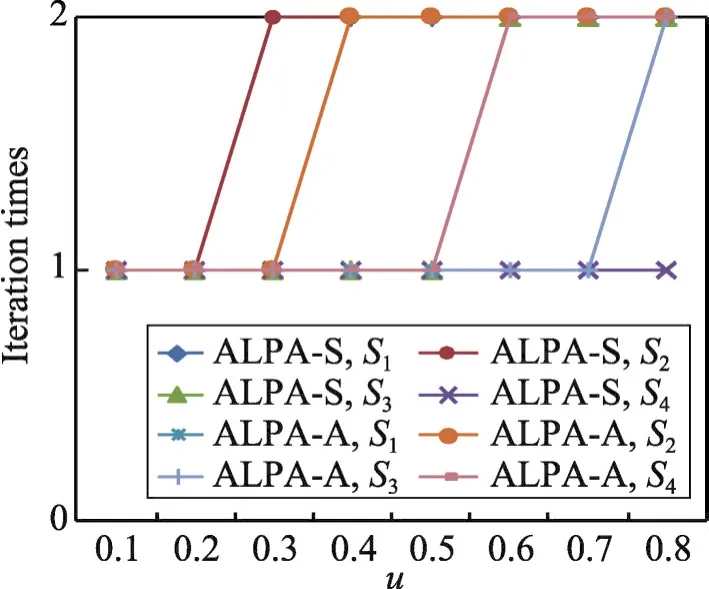
Fig.6 Iteration number of two kinds of algorithms on 32 artificial networks图6 两种算法在32个仿真网络上的迭代次数
ALPA-S和ALPA-A两种算法均提出极大团MC是社区的核心结构,社区内的其他节点应该围绕在极大团的周围。使用实验中的迭代次数来进行验证,结果如图6所示。图6显示了同步算法ALPA-S和异步算法ALPA-A分别在32个仿真网络上进行实验算法收敛时需要的迭代次数。结果表明两种算法在32个仿真网络上收敛时所需要的迭代次数均为1~2次,说明极大团MC是社区的核心结构,其余节点在MC的周围且通过1~2步即可到达MC中的节点。也进一步说明了两种算法的迭代计算代价是比较小的。另外,通过在32个仿真网络上的迭代次数计算可知,这两种算法都极容易收敛。其中,ALPA-S在32个仿真网络上的平均迭代次数是1.438,而ALPAA则是1.375。这也进一步说明同步算法需要更多的迭代次数才能够使算法收敛,而异步算法的收敛速度较快。
4.3 和其他算法的对比
(1)仿真网络上的实验
使用32个仿真网络数据集(如表1的S1、S2、S3和S4所示)对比ALPA-S算法、ALPA-A算法和其他几个经典算法如LPA算法、COPRA算法、DEMON(democratic estimate of the modular organization of a network)算法[27]和GCE(greedy clique expansion)算法在稀疏和稠密复杂网络上的社区检测性能。结果分别如图7中的(a)~(d)所示。
图7展示了相关算法在4种类型32个仿真网络S1、S2、S3和S4上的社区检测质量,分别如图7中的(a)~(d)所示。从图7可以得出如下结论:
①LPA算法、COPRA算法、GCE算法和ALPA-A算法在不同类型的复杂网络上的社区检测质量不稳定;
②ALPA-S算法和DEMON算法在混合参数μ值逐渐增加,社区结构逐渐不清晰的情况下,无论在稀疏还是稠密复杂网络中均呈现了较好的社区检测质量。
(2)真实网络上的实验
在5种真实社会网络数据集上继续验证所提算法的社区检测质量,并使用模块度函数Qov作为评价标准,结果如图8所示。从图8可以得出如下一些结论:
①ALPA-S算法在5种真实社会网络上的社区检测质量总体好于其他5种算法;
②ALPA-A算法在不同社会网络上的社区检测质量仍然表现出了一定的不稳定性;
③在仿真网络实验中一直表现较好的DEMON算法,在真实社会网络中的社区检测质量却明显表现不佳。
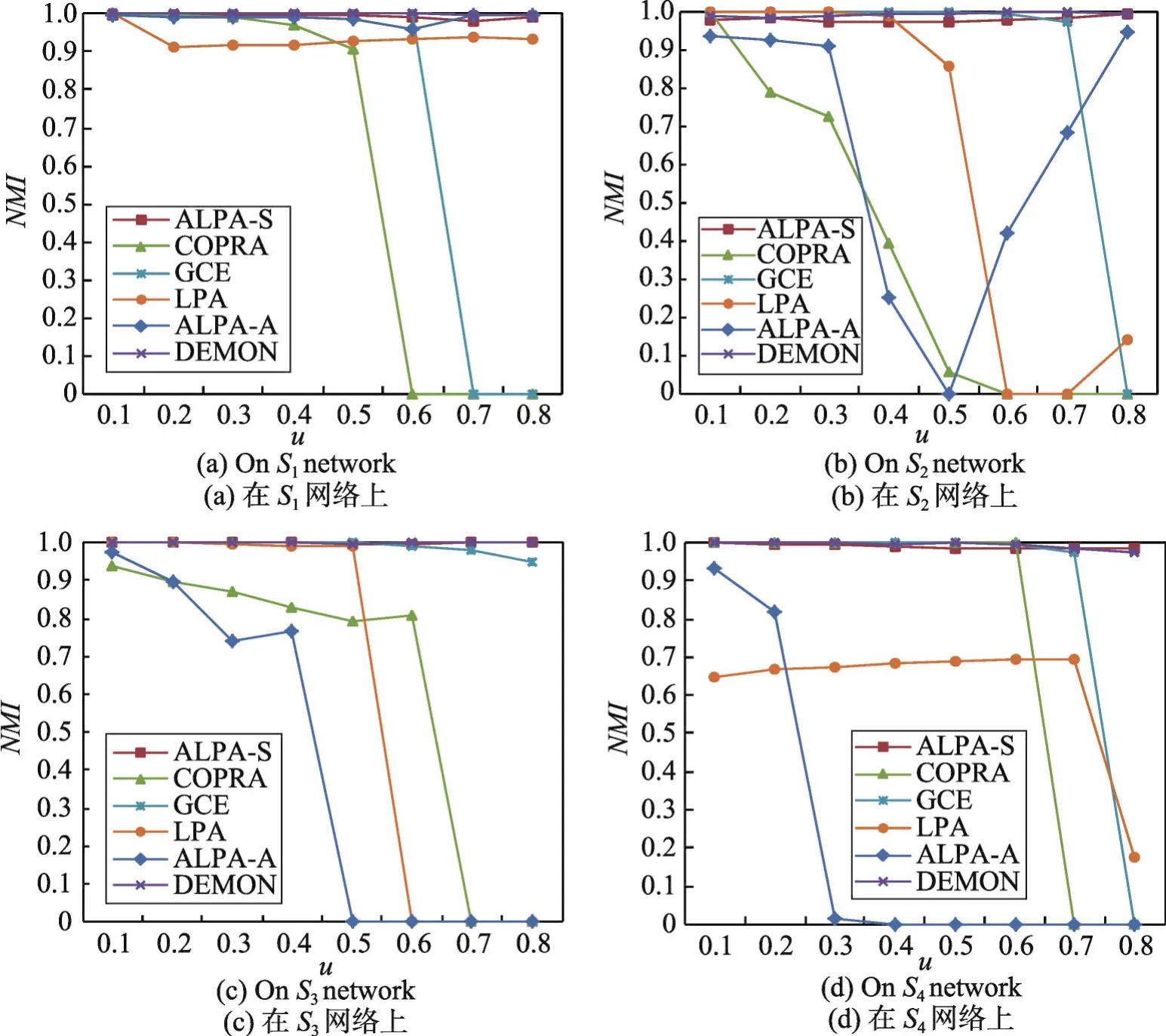
Fig.7 Result of community detection of related algorithms on 4 kinds of benchmark networks图7 相关算法在4种类型仿真网络上的社区检测质量
同时,在5种真实社会网络上检验算法在初始化时产生的标签节点比及算法的迭代次数,以便进一步验证本文提出算法的性能,结果分别如图9和图10所示。从图9和图10中可以看出,不同真实复杂网络被ALPA-S算法初始化后产生的标签节点比差异较大。其中,电力网络Power初始化后的标签节点比仅为4.37%,而迭代次数却多达10次和7次,这和仿真网络上的实验结果有较大的不同。因此,对使用ALPA-S算法通过最后一次迭代才能拥有标签的节点所在的社区之一进行了可视化分析。选中的社区包含100个节点,为了绘图方便,对该社区中的100个节点重新映射编号,可视化结果如图11所示。从图11可以看出该社区呈现近似树状的拓扑结构特征,并且其仅包含1个极大团{26,67,71},如图11红色部分所示,其余节点均围绕在该极大团的周围。从这些结果可知,Power中极大团数量较少,因此初始化时其获得的标签数量亦较少,这解释了图9中Power网络具有较小的标签节点比以及需要较多迭代次数的根源。另外,从图8可知,ALPA-A算法在Power上的表现好于其他5种算法,这也许可以说明当社区中的核心结构较少时,异步算法能够更快收敛的同时,亦能取得更好的社区检测质量。
综上所述,通过仿真网络和真实网络上的实验表明,异步算法ALPA-A能够更快地使算法收敛,其在社区核心结构较少的社会网络中能够取得较好的社区检测质量,但是在不同类型复杂网络中的社区检测质量仍然不够稳定。而同步算法ALPA-S无论在稀疏或稠密、社区结构明显与否以及在各种不同类型的真实社会网络中的社区检测质量均优于其他社区检测算法,体现了其具有较好的自适应性、稳定性和健壮性。
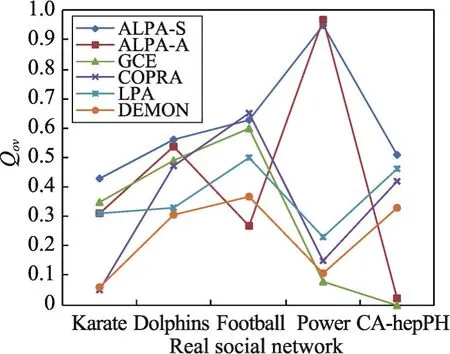
Fig.8 Modularity of community detection of related algorithms on 5 real social networks图8 相关算法在5种真实社会网络上的社区检测模块度
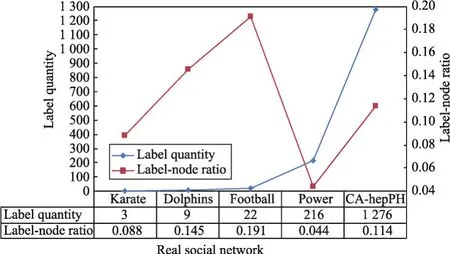
Fig.9 Number of labels and label-node ratio of ALPA-S algorithm on real social networks图9 ALPA-S算法在真实网络上的标签数及标签节点比
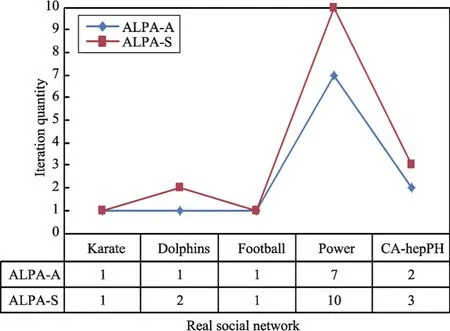
Fig.10 Iteration number ofALPA-S algorithm on real social networks图10 ALPA-S算法在真实社会网络上的迭代次数
5 结束语
由于依靠网络拓扑结构信息对社会网络社区结构进行挖掘具有模型简单、计算效率高和易于应用等特点,本文提出了单纯依靠社会网络拓扑结构信息的同步自适应标签传播算法ALPA-S和异步自适应标签传播算法ALPA-A检测复杂网络中的社区结构。通过对两种算法的性能分析以及和其他经典算法的对比,表明同步算法ALPA-S更适合于检测不同类型社会网络中的重叠社区结构和非重叠社区结构。另外,不需要参数控制的ALPA-S算法能够根据复杂网络的拓扑结构信息自动调整初始化时极大团中节点的个数以及根据节点标签个数自动调整阈值并剔除无意义的标签,具有良好的自适应性。因此其能更好地适应没有先验知识的真实社会网络。另外,本文提出的算法证实了一个社会现象:一个社区结构(群体)至少包含一个影响力较大的核心群体(极大团MC),社区影响力较弱的群体则围绕在影响力较大的核心群体的周围。下一步,考虑将ALPA-S算法进行并行实现,从而可以更好地解决大规模以及超大规模社会网络中的社区检测问题。
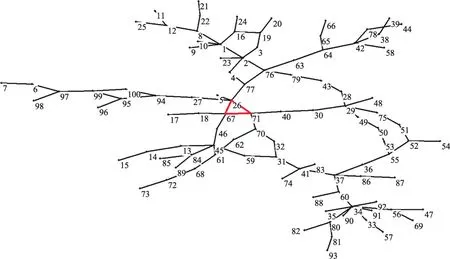
Fig.11 Graph of visualization result of a community in Power social network图11 Power中一个社区的可视化结果图
