复杂信息网络的弹性评估和优化方法研究*

齐小刚，张碧雯+，刘立芳，胡绍林

1.西安电子科技大学 数学与统计学院，西安 710071

2.西安电子科技大学 计算机学院，西安 710071

3.航天器故障诊断与维修重点实验室，西安 710043

4.西安理工大学 自动化与信息工程学院，西安 710048

1 引言

计算机网络应用在支持各类服务上发挥着越来越关键的作用。事实上，这些应用已经成为人们日常生活的一部分。医院、企业、学校、政府的日常运作越来越依赖于计算机网络服务。这些公开可用的网络服务不仅容易受到地震、飓风、海啸等自然灾害的影响，而且随时会发生各种故障状况以及面临一些网络攻击，使得正常的运作和服务中断。网络弹性[1-3]指的是网络在应对多种故障和挑战下，提供和维持可接受水平内的服务而正常运作的能力。因此构建具有良好弹性的网络拓扑用于应对挑战并且提供可接受水平的服务，可以延长网络寿命、节约网络成本。

一般网络，尤其是全球互联网，已经成为商业和全球经济的日常运作的必要内容。因此网络中断的后果[4]也变得越来越严重。现在广泛认为当前的许多现实网络不具备足够的弹性，需要相应的研究、开发和工程项目来完善基础设施网络和服务网络[5-7]的弹性。对于弹性网络结构的研究，Kumar等人[8]从复杂网络拓扑的角度提出一种DLA模型构建弹性供应网络，并且分析所提出的网络构建模型所构造的网络拓扑在应对随机故障和恶意攻击方面的弹性，当然网络构建过程不总是从头开始建立，因此不能解决对于现有网络的弹性优化问题，同时该模型只考虑了节点最大度这一项约束，远远不适用于现实网络的构建过程。李云冀等人[9]考虑拥塞造成的网络故障，对网络节点和链路的重要性进行评估，基于网络的邻接矩阵，构建在度约束下最小化平均距离的优化网络，提高网络的可生存性。然而，相比于构建弹性网络，也有大量研究着手于网络拓扑的优化，改善现有网络的拓扑，使其弹性应对各种挑战和故障。对于真实的服务提供者骨干网络拓扑，如Sprint、AT&T、GÉANT2等网络拓扑[10]的研究，综合比较拓扑的结构特性，如平均节点度、聚类系数、平均最短路径、半径和直径等。相比于表征网络连通性和健壮性的这些经典的图论指标[11]，图谱理论度量标准是图的健壮性指标的另一个子类，研究图的结构特性与相关矩阵的特征值和特征向量之间的关系。一些图谱指标可以用于测量移除节点或者链路之后图的健壮性，如代数连通度[12]、谱隙[11]、自然连通度[13]、权谱[14]、网络关键度[15]。Alenazi和Sterbenz[11]提出中心性攻击下的3种网络弹性测度，使用经典图论指标和图谱论标准，测量随机故障和恶意攻击下的网络弹性，以基本图和随机图为拓扑数据集，使用非线性相关比较各项指标预测攻击下网络弹性的准确度。

本文研究的图健壮性指标为网络的平均效率函数[16]。对网络施加随机故障和中心性攻击，测量网络的流健壮性，用该指标表示每次攻击下可靠流的可用性。每次节点攻击下的流健壮性作为网络的弹性测度。本文提出一种迭代算法优化网络的连通性，通过对给定图添加链路集来最大化网络的平均效率函数，提高网络弹性。将该算法用于3种复杂网络拓扑并且比较算法的效益。通过采用随机故障和基于中心性的攻击，测试和评估原始图和改善图的网络弹性。本文的主要工作为：提出了一种优化算法基于网络的平均效率这一健壮性指标改善给定图；对3个复杂网络使用该算法产生相应的改善图；使用流健壮性函数评估随机故障和中心性攻击下的网络弹性。

2 背景和相关工作

2.1 图中心性度量

给定图G=(V,E)，节点集V，边集E。中心性指标表示图中节点或者链路的重要程度。由于在不同的应用中节点或者链路的重要程度不同，一些指标可以基于给定的应用作为指示器来确定中心节点。

节点度中心性CD(v)定义为节点关联的链路数，可以看作是节点连接的重要性。节点度是一种局部的中心性指标是由于它只依赖于局部连接的链路数。平均节点度表示为(v)。节点i、j之间的最短路径dij为连接两点之间跳数最小的路径。平均最短路径长度衡量网络平均跳数。一些常用的图度量标准如介数、半径和直径提供了所有节点对之间最短路径的统计值。介数是一种可以用于节点和链路的中心性指标。节点介数CB(v)为经过节点v的最短路径的数目，而边介数CB(l)定义为经过链路l的最短路径数。介数具有全局意义是由于介数反映的是图的整体结构。节点紧密性CC(v)是衡量节点v到其他节点平均距离的中心性指标。聚类系数CC(v)衡量节点v的邻点全连接的程度。

2.2 相关图谱理论知识

现有的一些研究用来量化恶意攻击和随机故障下图的健壮性[3]。这里根据所提出的健壮性指标和评估方式，介绍每项指标的公式化表示及其预测中心性攻击下网络弹性的准确度等[11]相关工作。图谱理论研究的是图的结构特性与图的邻接矩阵、关联矩阵、拉普拉斯矩阵和标准化拉普拉斯矩阵的特征值和特征向量之间的关系[17]。

给定图G=(V,E)，节点集V,边集E，节点数为N，边数为K。A=(Aij)N×N为图G的邻接矩阵，其中：

特征值μ为特征多项式det(A-μI)=0的根。{μ1,μ2,…,μN}为邻接矩阵的特征值集合，元素呈递增排列。谱隙定义为Δμ=μN-μN-1，为邻接矩阵的最大特征值与第二大特征值之间的差，是衡量恶意攻击下图健壮性的一个图谱指标[11]。自然连通度定义为，其中μi为邻接矩阵的第i个特征值。自然连通度的值越大，网络应对节点或者链路移除的健壮性越强。相比于平均节点度，自然连通度[13,18]在描述网络弹性时更加准确。

3 网络弹性优化算法

3.1 网络模型

一般的，将网络表示为具有N个节点、K条边的无向加权图G=(V,E)，V={v1,v2,…,vN}为节点集合，E为边的集合，eij∈E表示节点vi,vj∈V之间的链路。A=(Aij)N×N为图的邻接矩阵。假设节点对之间的网络流选择两点之间的最短路径通信。εij表示节点vi和vj之间使用最短路径通信的效率，定义为节点对之间最短距离的倒数，表示为εij=1/dij，其中dij表示节点间最短距离。这里假设效率与距离之间成反比，当图中节点vi和vj之间不存在路径时dij=+∞，相应的εij=0。那么网络的平均效率定义为：

即节点对之间最短距离倒数之和的平均值，用于测量G的效率或者性能，表示网络平均通信的容易程度。E(G)的值越大，表示网络的连通性越强。优化网络的平均效率改善网络拓扑，可以提高网络的运作效益和稳定性，提升网络应对随机故障和恶意攻击下的弹性[19-20]。

进一步，对于无向加权网络G=(V,E,W)，W=(wij)N×N为考虑边权之后的邻接矩阵，当节点vi、vj之间有边相连时wij为边eij的权值，否则wij=∞。wij的值可以认为是从节点vi到节点vj的距离或者成本。设p(i,j)是加权图中节点vi到节点vj的路径，则，其中w(e)为边e的权值，E(p)表示路径p上边的集合。那么节点vi、vj之间的最短距离，P为节点vi、vj之间所有路径的集合。同理，可以定义加权网络中的网络平均效率。

3.2 优化算法

本文使用一种启发式算法，对给定图Gi添加链路集。优化算法的目标是选择Lr条链路的集合最大化网络的平均效率这一健壮性指标，即maxE(G)。算法迭代地选择满足目标函数的链路加入网络改善网络弹性。如下为拓扑优化算法的伪代码。

拓扑优化算法的两个输入：初始图Ai和所需链路数Lr。输入图Ai的节点数为Ni，链路数为Ki。所需链路数Lr为网络图中所需添加的链路数，由于现实中较少出现全连通网络，考虑到网络成本的约束，对网络常见失效模式的防御和对于网络性能的要求等因素可能只需要该网络达到一定水平的健壮性而不一定需要百分之百可靠的网络，因此只需要添加特定数量的链路，或者出于对现实中预算资金和现实网络环境的考虑需要添加与约束相关的相应数量的链路，因此本文使用所需链路数这一参数作为算法输入，并且链路数量由现实成本或者备选链路集合中链路的数量等决定。为了记录迭代过程所选定的链路，算法将链路加入selectedLinks列表。每次迭代开始于上一次迭代所得图，并对其添加链路。算法使用3个主函数：efficience(G)、candidate(G)和improvedLink(L)。平均效率函数efficience(G)返回给定图的平均效率值，为该优化算法的目标函数，根据3.1节的定义和公式，需要根据网络的最短路径算法求出节点对之间的最短路径矩阵，计算网络相应的效率矩阵，最后返回网络的平均效率。备选链路函数candidate(G)以图G为输入，返回备选链路的集合，该链路集合由当前图G中节点间不存在的边组成。当前图Ai中不存在的链路的数目为为图Ai中的节点全连接状态下的链路数减去当前图Ai中的链路数。随着ni的增大，其计算复杂度不断增加。优化算法不断产生新解，于是需要在所有可行解中找出相对最优解，使用improvedLink(L)函数，可以从candidate(G)函数选出的备选链路集合中选出最大程度上将图的平均效率值改善的链路，添加到链路集合selectedLinks中。算法重复迭代直到选出足够的链路，并且添加到初始图中，得到最后的改善图G。

拓扑优化算法的具体步骤为：第一步，执行伪代码第1行到第3行，初始化链路集合selectedLinks和迭代链路iterationList列表；第二步，执行第7行到第9行的for循环，对于图G的候选链路集合candidate(G)中的链路l，计算添加链路l后图G的平均效率函数efficience(G)赋值给中间变量improvement，同时将链路l和函数值记录到iterationList列表；第三步，执行算法伪代码10到12行，对列表iterationList中记录的链路施加函数improvedLink(L)选择出使得平均效率函数改善效果最大的链路，并添加到selectedLinks链路列表，同时在图G上添加该链路得到该迭代过程的新图；第四步，执行第4行的While循环，如果selectedLinks列表中的链路数小于所需添加链路数Lr，转到第二步，否则，返回selectedLinks和图G，算法结束。

4 弹性测量

本章首先介绍如何使用图的流健壮性[10,16]度量标准衡量网络弹性。然后，给出用于弹性评估的攻击模型，以及所研究的3种复杂网络拓扑。最后，使用流健壮性指标量化节点攻击下的网络弹性。

4.1 流健壮性

流健壮性是一种图论度量标准，测量可靠流的数量占网络中总的网络流数量的比率。网络流称为可靠流，如果存在节点或链路故障时节点对之间至少有一条路径保持正常。总的网络流数量为网络中可能存在流的最大数量，对于N个节点的网络，总的流数为N(N-1)/2。该标准衡量移除节点或链路之后，网络节点与其他节点通信的能力。流健壮性的取值范围为[0,1]，1表示网络中的任意节点对之间可以通信，即网络为连通图；0表示整个网络中不存在可以通信的节点对，即网络中不存在链路。给定网络图G=(V,E)，集合{Ci;1＜i＜k}表示图G的连通分支。网络的流健壮性表示为：

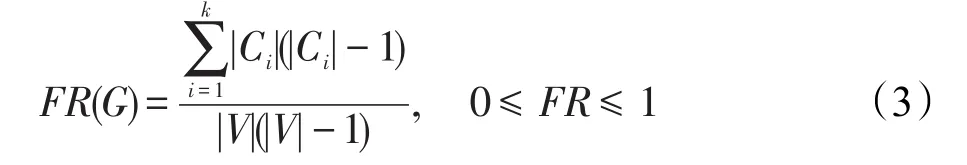
计算FR的算法复杂度取决于给定图中寻找连通分支的复杂度，为O(|V|+|E|)。由于k的最大值可能取为|V|，最坏情况的复杂度可能为|V|。因此计算流健壮性的算法复杂度为O(|V|+|E|+|V|)，简化为O(|V|+|E|)。本文使用流健壮性指标是因为：第一，它与网络仿真中对于所有的节点对之间以给定的比特率通信的包递交率结果匹配；第二，它能有效地评估网络的连通性。

下面以一个9个节点的车轮形拓扑为例，通过计算介数攻击下的流健壮性值，说明如何测量网络弹性。在每次迭代中，移除一个节点并且计算流健壮性值。节点删除列表可以由节点攻击的任何可能方式定义。例如基于最高的介数值依次攻击节点，产生节点列表{0,1,5,3,7,8,2,4,6}。图1描述了连续攻击下的网络拓扑。其中浅绿色节点表示节点未被攻击处于连通状态，深红色节点为攻击节点表示不连通状态的节点。节点一旦被攻击，连接该节点的所有链路将被移除。每次迭代过程的健壮性值如表1。Step 2中，删除节点0之后将移除8条链路，而流健壮性值减少0.22，此时其他节点可以使用备选路径通信。然而Step 4中，流健壮性值减少0.58-0.17=0.41，由于图被分割为两个分支造成了流健壮性的减少量最大。在Step 6之后结束，此时图中无剩余链路。

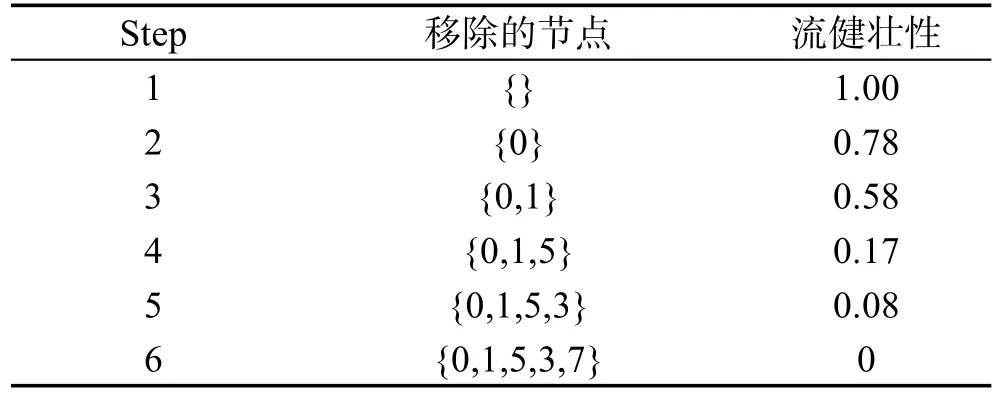
Table 1 Flow robustness values of wheel topology表1 车轮形拓扑的流健壮性测量

4.2 图的攻击模型

本文使用图论模型攻击给定的网络，说明每次节点移除后网络的流健壮性如何变化。使用随机故障模型和3种中心性测量标准：节点介数、节点紧密度和节点度。针对3种中心性测度[6]分别使用3种攻击模型，移除中心性值最高的节点。节点介数攻击的目标是最短路径经过次数最多的节点。节点紧密性攻击的目标是与其他节点跳数最近的节点。节点度攻击移除的是具有最多邻点的节点。节点移除列表根据不同的攻击模式自适应地产生。自适应节点移除与非适应性移除相比，每次移除当前网络中中心性最高的节点。

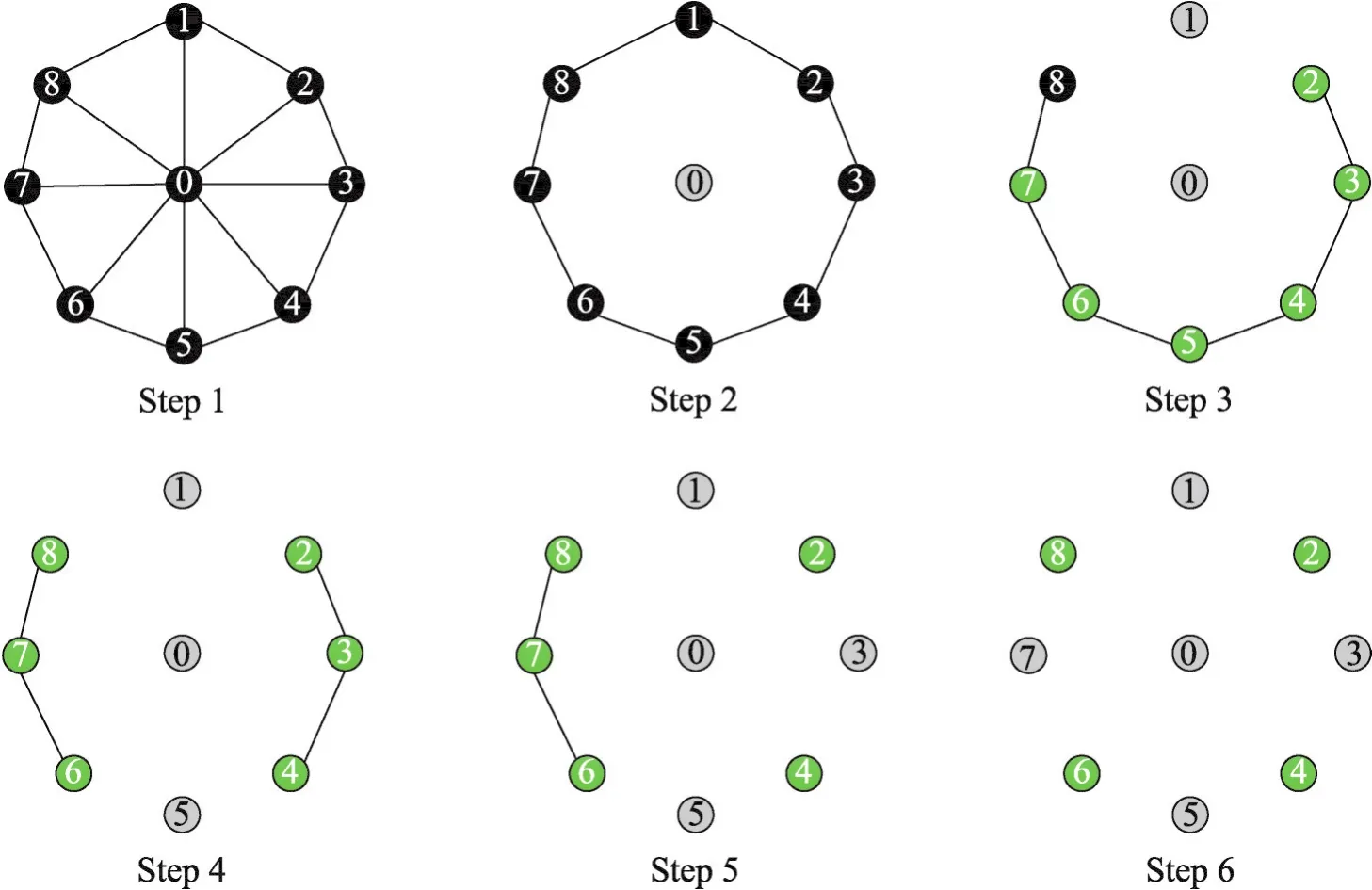
Fig.1 Wheel topology under betweenness attack图1 介数攻击下的车轮形拓扑

4.3 数据集

本文采用3种拓扑结构测量所提出算法的有效性，评估它们在随机故障和恶意攻击下的网络弹性。包括典型的复杂网络模型如ER随机网络模型和BA无标度网络模型，以及一种保证节点数和平均节点度的拓扑产生模型，简单记为AD连通网络。为了方便了解本文所提出算法对网络的优化状况，文中以车轮形网络拓扑为例说明所提出的优化算法如何实现对网络拓扑健壮性的改善，因此所研究的重点还是复杂网络拓扑模型。另外，列出每种拓扑的经典图论指标表现图的拓扑特性，包括节点数、边数、平均度和平均跳数，如表2所示。然后，将本文所提出的最优化算法应用于这4种网络拓扑，对每种网络拓扑运用提出的最优化算法改善拓扑，评估网络弹性。

5 仿真及分析

本文使用流健壮性指标量化网络弹性，使用图的平均效率这一最优化目标函数，采用加边策略实现对于网络拓扑的优化，提升网络应对随机故障和恶意攻击下的网络健壮性。本章执行前面提出的弹性优化算法，对规则的车轮形网络和3种复杂网络分别添加与该网络节点数相同数目的链路，即对9个节点的车轮形网络拓扑添加9条链路，对节点数为50的ER随机网络添加50条链路，优化算法中的输入Lr设置为50，同理对于BA无标度网络和AD连通网络分别添加75和50条链路，使得网络的平均效率函数最大化。对于上述4种网络拓扑，算法输入的初始图的网络平均效率值non-improvedAE（average efficiency）和使用该算法改善后优化网络的平均效率值improved AE由表3的第三列和第四列给出。

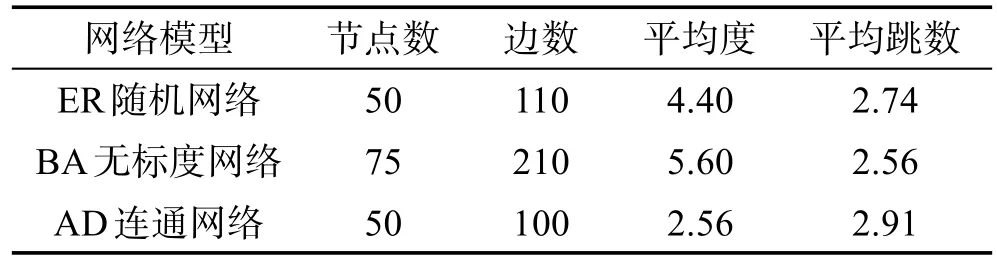
Table 2 Dateset of topology表2 拓扑数据集

上述拓扑是本文仿真实验使用的主要网络拓扑，在实验中先使用选定的网络拓扑模型生成相应的初始网络拓扑，每种网络拓扑模型生成10种具体网络拓扑，然后使用弹性优化算法得到网络改善图，对每种拓扑模型中生成的每一个网络拓扑进行20次优化实验，并对每一次优化网络施加随机故障和3种恶意攻击，记录每个网络的性能衰落表现，最后将每一个网络拓扑多次性能衰落数据相应取平均作为该拓扑的性能表现，对同一类型下的多个网络拓扑进行统计作为每一种拓扑模型的性能表现，从而进行弹性性能对比，评估所提出算法的性能。使用的操作系统为Windows 7，实验编程硬件环境：处理器为Pentium III 933 MHz或以上级别，内存128 MB或以上，硬盘可用空间100 GB或以上，软件环境Matlab 7.1或以上。

Table 3 Average efficiency of non-improved and improved graphs表3 初始图和改善图的平均效率

仿真过程使用图论模型攻击给定图，并且给出网络的流健壮性随每次攻击的改变情况。分别使用随机故障模型和3种中心性（介数、紧密度和节点度）攻击模型，每次迭代删除中心性值最高的节点，节点的删除列表随着攻击模型的不同而改变。

对于本文提出的以平均效率为优化函数（AE-improved）的拓扑改善算法，使用两种优化算法进行对比，比较算法的改善效果。一种为参考文献[13]中使用的网络自然连通度改善算法（NC-improved），即选择自然连通度作为健壮性指标对网络拓扑进行加边优化，输出网络的改善图。另一种为参考文献[11]中出现的网络谱隙优化算法（SG-improved），以初始网络拓扑（non-improved）作为输入，图谱理论中的谱隙标准作为优化函数，对网络迭代地添加指定数量的链路以改善网络的连通性，输出改善图。

对于每种网络拓扑，给出相应的网络初始图（non-improved）、本文提出的平均效率改善拓扑（AE-improved）、两种对比算法的自然连通度改善拓扑（NC-improved）和谱隙改善拓扑（SG-improved），采用随机故障和3种攻击模型删除对应网络中半数以上的节点，在攻击模型下各种拓扑的健壮性表现不同，采用流健壮性指标评估网络弹性，仿真结果如图2～图5。

以车轮形拓扑为例，图2（a）～图2（d）分别表示的是该拓扑在随机故障和3种中心性攻击下网络的健壮性变化情况。图2（a）中，在随机故障模型下，每删除一个节点，剩余的节点在同一个连通分支中，相互保持连通，因此对于初始图和3种改善图网络的健壮性表现一致。图2（b）与图2（c），由于车轮形拓扑的特殊性，介数攻击和紧密度攻击产生相同的节点删除列表，此时3种网络改善图相比于初始图健壮性有所增强，同样的现象出现在图2（d）中。在车轮形网络拓扑中，所提出的平均效率改善算法的改善效果与两种对比算法无明显差别，这是由于车轮形网络节点之间最多两跳可达，加边过程实际上是增加一跳可达的节点对的数目。当网络中增加9条链路时，基本可以保证每删除一个节点，其他节点保持相互连通的状态，即网络的流健壮性在删除节点后保持所能维持的最佳状态。而对于3种典型的复杂网络而言，不同的拓扑优化算法所表现出的网络健壮性明显不同。

ER随机网络在随机故障模型下的网络健壮性如图3（a）所示。在节点攻击模型下，本文所提出优化算法，即平均效率改善拓扑的流健壮性随节点移除数量的变化用黑色带星号的曲线表示。在ER随机网络的流健壮性分析仿真图3中，自然连通度改善图、谱隙改善图、初始图在故障模型下的流健壮性随删除节点数的变化分别为蓝色、品红和红色曲线。介数、紧密度和节点度攻击模型下的网络弹性分析分别如图3（b）、图3（c）、图3（d）所示。从仿真结果可以看出，对于ER随机网络，本文所提出的算法改善网络拓扑的效果最好，应对随机故障和恶意攻击具有较高的网络弹性。该结论在BA无标度网络模型和AD连通网络模型中同样成立。BA网络和AD网络在随机故障和恶意攻击下的流健壮性仿真结果如图4、图5所示。代表网络平均效率改善算法的黑色曲线整体处在其他曲线的上方，具有较高的流健壮性值。虽然图5（c）中BA网络处于节点度攻击下黑色曲线少量点的流健壮性值低于品红色曲线，实验分析不排除出现这种情况的可能性，但是整体的仿真结果说明本文的优化算法较其他算法而言具有明显的优势。由于网络弹性量化为删除节点下的流健壮性值，值越大，网络应对攻击下的弹性越强。通过研究表2中的网络模型，结果表明本文提出的加边优化算法，相比于另外两种对比算法，应对节点攻击方面表现出更好的网络弹性。

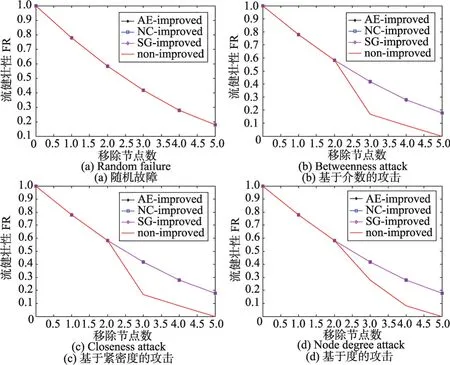
Fig.2 Flow robustness analysis of wheel topology图2 车轮形拓扑的流健壮性分析

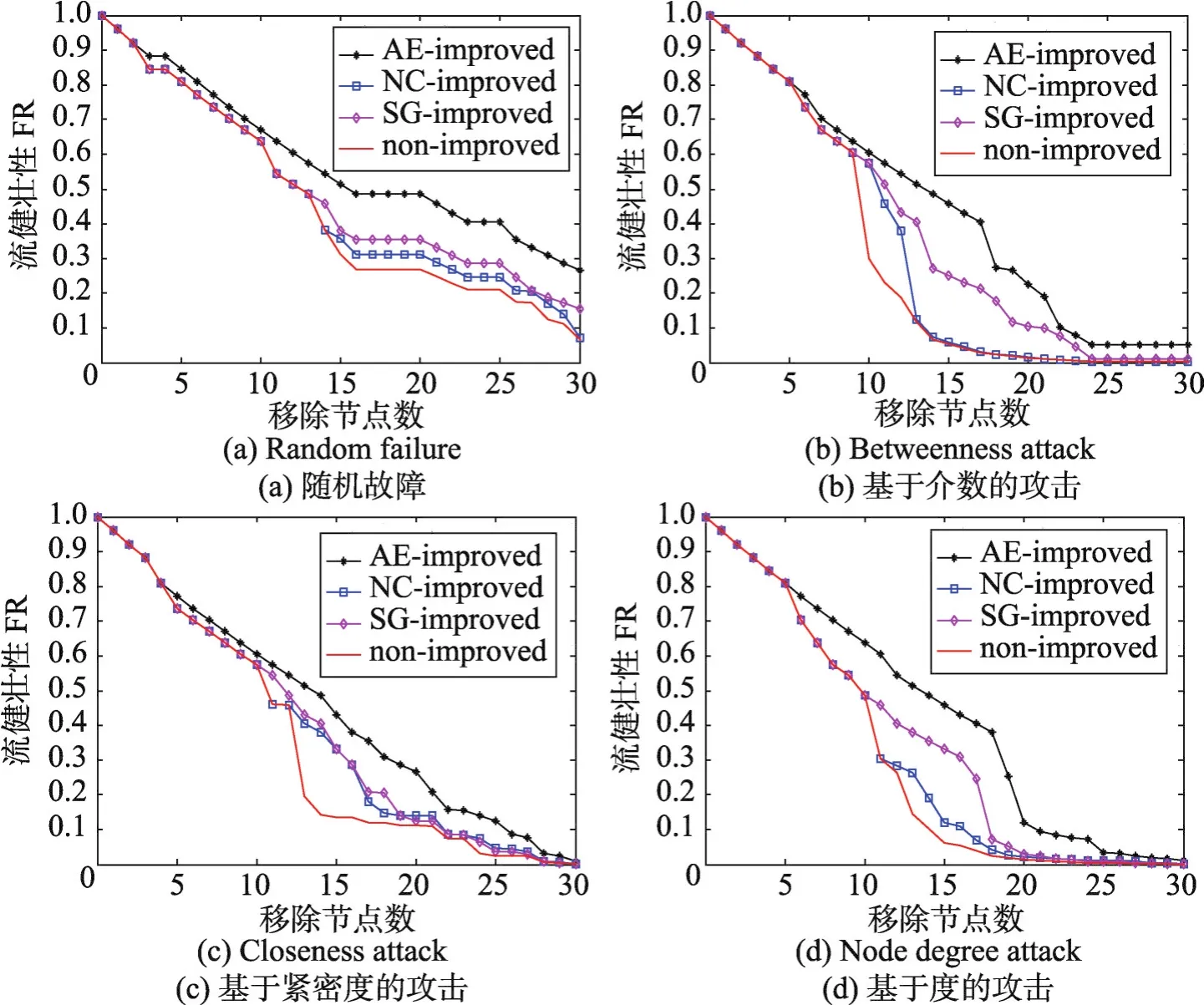
Fig.3 Flow robustness analysis of ER random network图3 ER随机网络的流健壮性分析

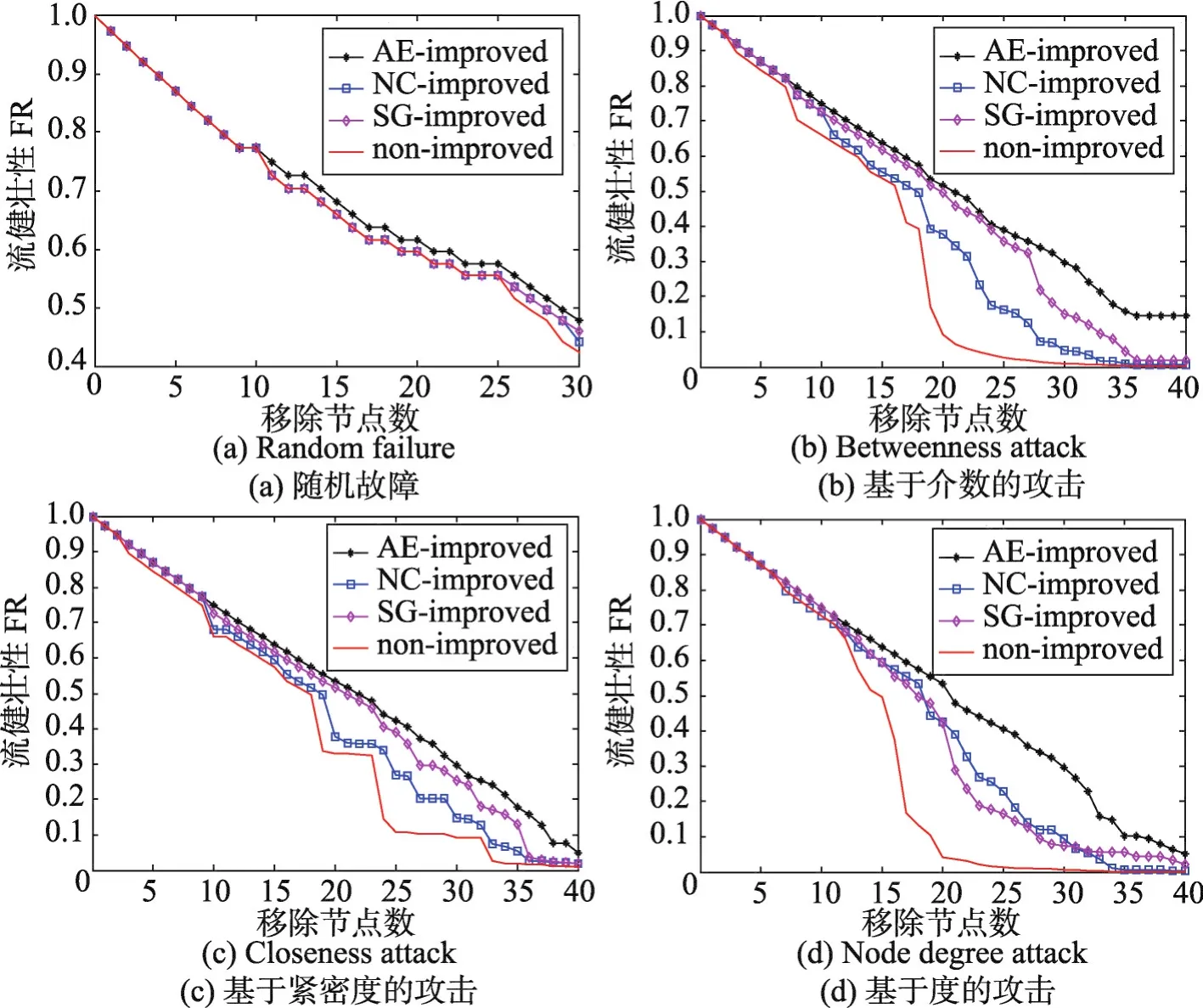
Fig.4 Flow robustness analysis of BAscale-free network图4 BA无标度网络的流健壮性分析

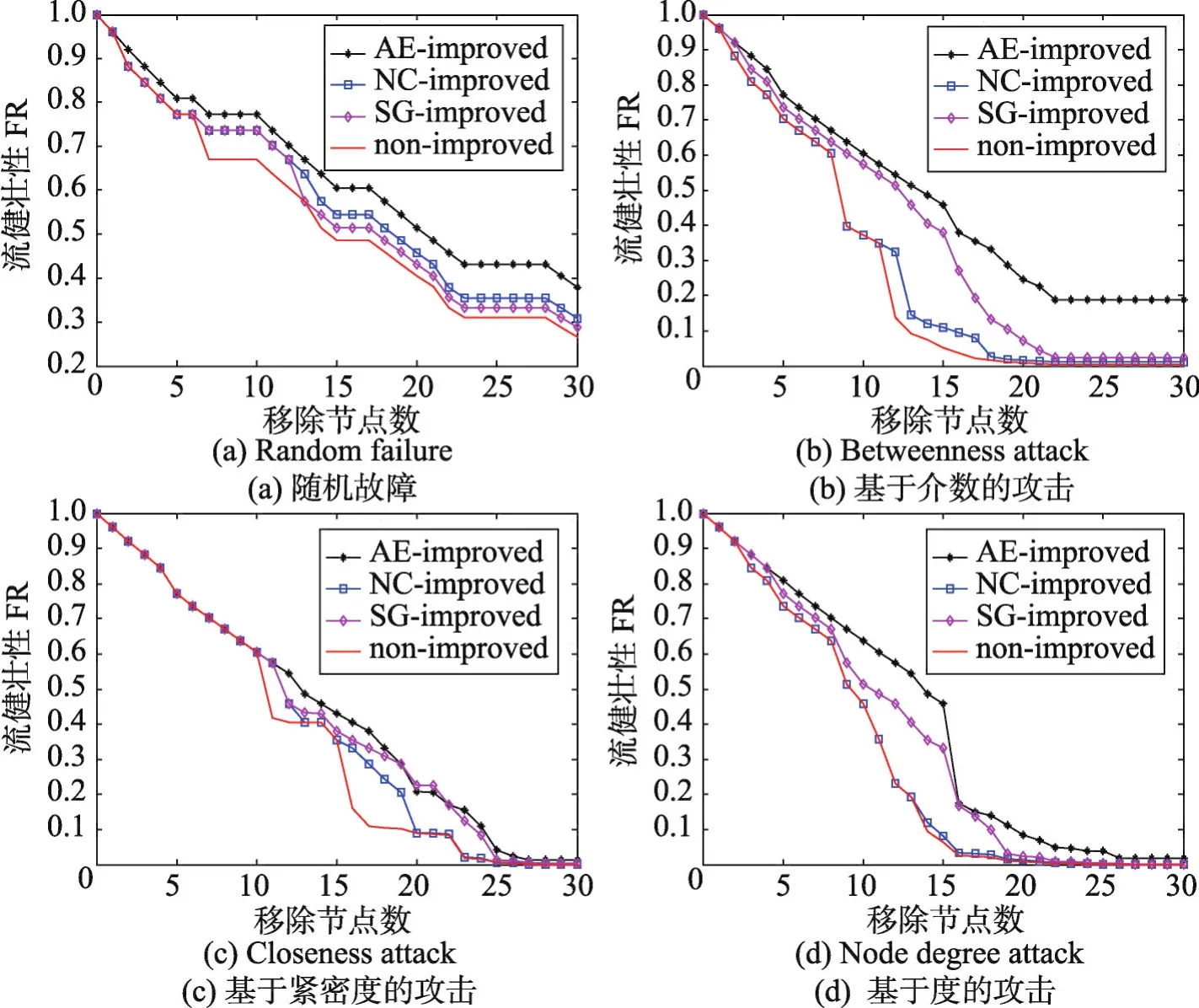
Fig.5 Flow robustness analysis ofAD connected network图5 AD连通网络的流健壮性分析

6 结论

网络设计和优化是复杂网络科学研究的一个重要领域，提出改善已有网络性能的有效算法，是复杂网络弹性研究的根本目的。本文提出一种迭代算法优化网络拓扑，对给定图添加链路改善网络的平均效率函数，提高网络弹性。将该算法用于3种复杂网络拓扑并且比较算法的效益。通过采用随机故障和基于中心性的攻击，测试和评估原始图和改善图的网络弹性。与图谱理论的一些健壮性优化算法进行对比，仿真结果表明在所研究的健壮性指标中，本文提出的启发式算法可以优化网络拓扑，相比于其他的改进算法在应对随机故障和中心性攻击方面更加具有弹性。人们逐渐加重的对互联网的依赖性以及服务的复杂化使得网络易于受到攻击，由于现实网络所面临挑战的多样性，使得未来网络的弹性设计以及现有网络的弹性改善变得尤为重要，因此，该算法在完善基础设施网络和服务网络的弹性性能方面具有实际应用价值。