基于可拓学的道路互通式立交方案优选模型及应用
2018-08-14杨胜波
杨胜波
(贵州省交通规划勘察设计研究院股份有限公司 贵阳 550001)
道路互通式立交方案的评价问题是一个相当复杂的系统问题,涉及到的因素众多,各因素很难建立经典的数学模型进行综合评价。传统上,道路互通式立交方案综合评价以工程经验法为主,常见如技术指标比较法、分项指标打分法等,但是工程经验法很大程度上会受主观经验的影响,导致评价结果不具有客观规律性。目前,基于层次分析法、灰色关联分析法、模糊理论等方法,众多学者构建道路互通式立交方案评价体系,获得了一些有意义的成果[1-2],这些评价体系一定程度上降低了人为主观性。层次分析法是一种定性与定量有机结合的多目标决策分析方法,一定程度上会依赖决策者通过经验给与量化,对于受多种因素作用的道路互通式立交方案的评价,则会带来较强的经验性色彩。灰色关联分析法通过设计一个最优的评价方案,然后计算各个待评方案与该最优方案之间的关联度,得到关联度最大的待评方案,即为各个待评方案中的最优方案,但是最优方案的指标体系是建立在人为主观经验的基础上,构建的最优指标体系也会因人而异。模糊理论评价主要是采用隶属度指标来综合确定各个方案的最优性,其评价结果很大程度依赖于所选取的隶属函数。
本文在前人研究成果的基础上,从道路互通式立交的技术指标、使用功能、经济指标、社会影响功能和管理功能5方面出发,运用可拓学理论,建立了道路互通式立交方案优选模型。
1 道路互通式立交方案评价指标
立交方案主要受技术性能、经济效益、使用功能、社会影响和管理养护费用等因素的影响,本文采用技术指标、经济指标、使用功能指标、社会影响指标和管理指标5个基本指标,构建道路互通式立交综合评价体系,见图1。
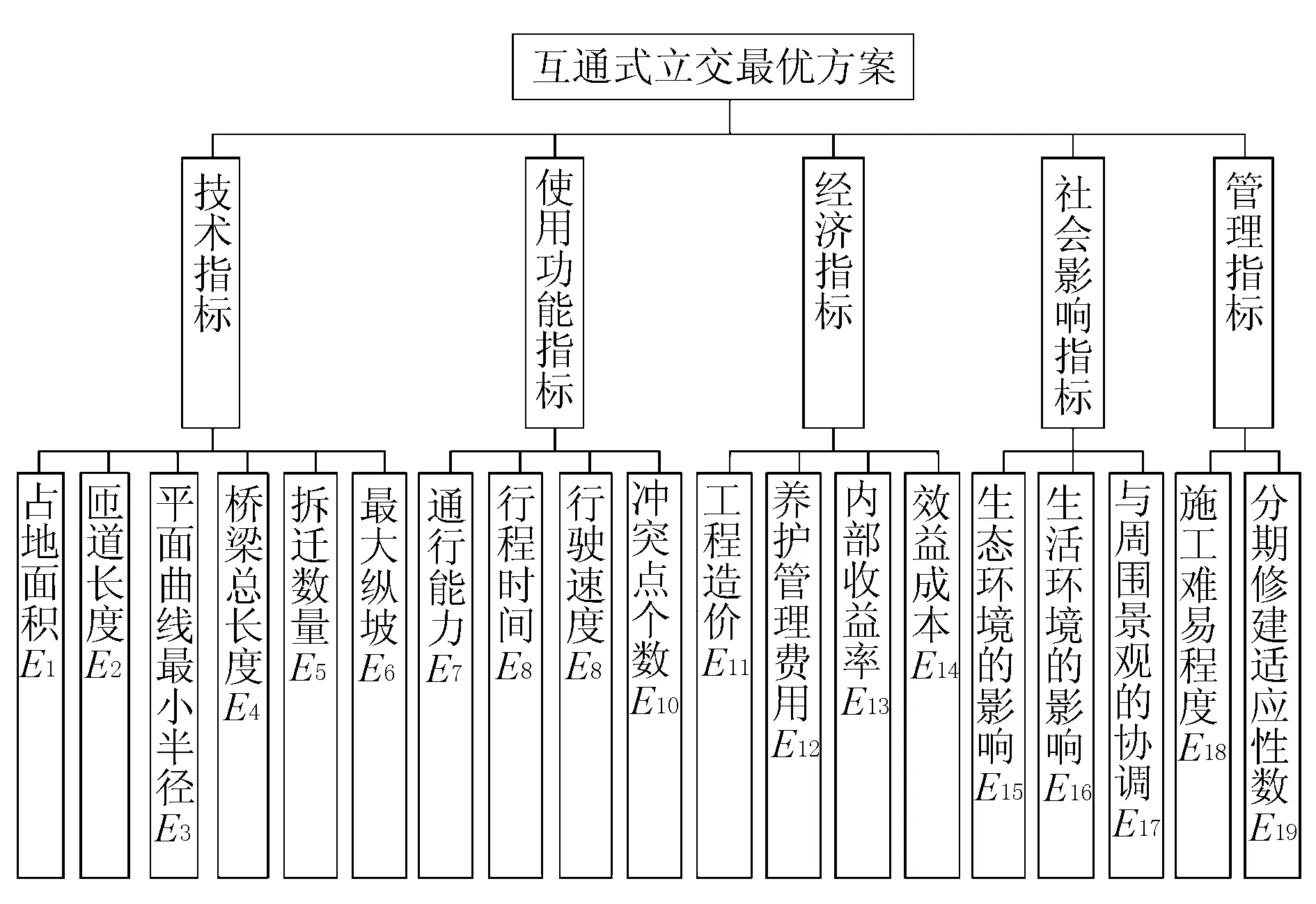
图1 道路互通式立交综合评价体系
2 基于可拓学的道路互通式立交方案评价模型
可拓学理论是以定量和定性的2个角度去揭示研究对象的本质规律,将研究对象N、研究对象具备的特征E及其特征反映的量化值E(N)构成有序的三元组,称之为物元[3], 记作:
R=(事物,特征,量值)=(N,E,E(N))
(1)
现将可拓学优度评价法应用于道路互通式立交方案比选中,具体步骤如下。
1) 待评方案物元的确定。指标体系的选择将决定道路互通式立交方案比选的合理性,本文通过了解该方案的特征以此确定所需要的特征指标。设评价指标集用E={E1,E2,…,En}来表示,并确定各指标值的取值,根据工程实际条件确定评价指标的容忍范围。

0~4评分法则的评分方式为:对选定的因素在同一层、层次间进行一一比较打分,这一过程在权重系数表中进行,当2个比较因素的重要程度被判定为一致时,则在对应的第i行第j列记入2分,因同等映射关系在第j行第i列也记入2分;当2个比较因素的重要程度被判定为不一致时,可将两者的重要性比较程度分为重要、很重要,依据比较程度进行打分,按上述2种情况进行具体描述,假如判定第i个因素较第j个因素重要时,则在第i行第j列记入3分,而在第j行第i列记入1分,假如判定第i个因素较第j个因素很重要时,则在第i行第j列记入4分,而在第j行第i列记入0分。现将第i行第j列的得分以aij表示,通过权重系数表可见,表中数据均满足aij+aji=4(i≠j),在i=j处不打分,然后得到每项指标总得分,以此可算出该指标的权重,见表1。
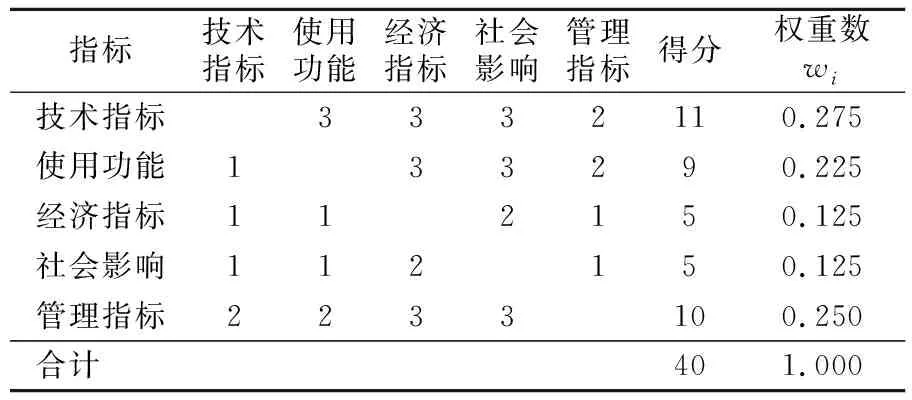
表1 道路互通式立交方案评价模型的权重表
3) 利用关联函数ki(x),计算合格度ki。按选定的指标集En和获得的权重wn,确立指标集的关联函数ki(x)[5]。
若Ei(N)用一个区间X0i表示,取
(2)
式中:|x0i|为区间的长度;ρ(x,x0i)称为距,它表示点x与区间X0i=[a,b]较近端点的距离,
(3)
对于等级标准区间内实际数据值定位问题,可拓学理论是一种比较好的处理手段。根据可拓学理论观点,当点x在X0i之内时,点x与区间X0之距为负值,负值大小确定点x在区间X0内的位置关系[3]。
当关联函数ki(x)的最优点在X0以内时,即x0i (4) 实际中某些指标最优点可能在合格区间之外,可能表现出越小越优或者越大越优的特征,在这种情况下,ki(x)应采用左侧距或者右侧距计算,即 (5) 在评价计算指标值表现出越小越优时,ρ(x,x0i)采用左侧距方式计算 (6) 在评价计算指标值表现出越大越优时,ρ(x,x0i)采用右侧距方式计算 (7) 通过以上建立方案Nm关于Ei的关联度ki(Nm)。 为了方便评价Nj,对ki(Nm)进行规范化处理[5],参评方案Nj关于评价指标的规范合格度为 (8) 则Nj关于Ei的规范合格度简记为 ki=(ki1,ki2,…,kim)i=1,2,…,n 4) 计算优度,确定最优方案。参评方案Nj关于指标集En的规范合格度为 故方案Nj的优属度C(Nj)为 (9) 按照可拓学理论判定,若C(N)>0,则表示被评价对象“得大于失”,若C(N)<0,则表示被评价对象“失大于得”,那么最优方案可记为 以文献[6]中给出的一个工程实例为例,结合文献[1]对该实例进行评价,验证本文方法的合理科学性。案例中针对某高速公路设计一座互通式立交,采用相同的设计技术标准,有3种设计方案可做选择,根据实际情况选择评价指标。 根据工程实际特点,确定比选方案的评价指标及指标值见表2。按照前述“0~4评分法则”得到了指标值的权重系数,见表3。 表2 某互通式立交比选方案的指标值及权重系数表 表3 某互通式立交比选方案各指标的权重系数表 3种比选方案N1~N3的指标集En,则待评方案物元为R1如下,R2、R3类似,此处省略。 根据工程经验和参考相关规范,该道路互通式立交的各个评价指标取值范围按表4所示基本准则确定[7-8]。 表4 各评价条件取值范围表 续表4 评价指标取值范围E9行驶速度/(km·h-1) 不能超过60,30~40可以接受,在40~50最好E10冲突点个数/个冲突点个数必须没有E11工程造价/万元 不能超过8 000,6 000~7 000可以接受,在4 000~6 000最好E12养护管理费用/万元 养护费用越低越好,但不能超过300万E13内部收益率/% 内部收益越大越好,但不能小于15%E14效益成本 效益成本越大越好,但不能低于1.2E15生态环境的影响影响越小越好E16生活环境的影响影响越小越好E17与周围景观的协调 与周围景观的协调越容易越好易E18施工难易程度施工越容易越好E19分期修建适应性 适应性越大越大越好,但不能小于6 由表2~4中的各项指标值及指标评价要求,按前述的可拓学理论分析评价方法,通过式(2)~(9)计算各比选方案的最优度结果,见表5。 表5 互通式立交比选方案计算优度值 由表5可见,3个比选方案优度值从大到小依次为:方案三、方案一、方案二,说明在该工程实际情况下选择方案三的环形立交方案为最佳的设计方案,这与文献[3]的工程实际是相符合的。 道路互通立交方案评价是一个评价指标众多、影响因素错综复杂的的决策问题,本文结合道路互通立交的特点,设计出道路互通立交方案评价指标体系图,运用可拓学理论中优度评价法,建立道路互通式立交方案优选模型。将构建模型运用至实际工程互通式立交方案比选中,评价分析得到最佳的设计方案,该方案符合实际情况。研究表明,本文构建的基于可拓学理论的道路互通立交方案优选模型,能够将各方案的影响因素进行最大限度量化,保护已有信息真实度,减少不确定性影响,模型算法简单易行,便于理解,结果符合实际,这将为设计师进行道路互通立交方案选择提供新的手段。3 工程实例





4 结语
