单管感应电能传输系统参数全局优化
2018-08-14赵志斌王春芳骆彬司剑飞于守淼
赵志斌, 王春芳, 骆彬, 司剑飞, 于守淼
(1.海军航空大学青岛校区, 266041, 山东青岛; 2.青岛大学自动化与电气工程学院, 266071, 山东青岛)
近年来,无线电能传输技术(WPT)因能有效地解决电源的便捷、安全接入等问题而受到广泛关注[1],研究热点主要集中在电磁感应耦合(ICPT)及磁共振耦合[2-3]。在中小功率ICPT领域,采用单个开关管实现谐振逆变的单管感应电能传输系统具有体积小、开关损耗低、性能可靠等优点,非常适用于中小功率家电、电子产品等无线供电[4]。
青岛大学王春芳等人研制成功一款传输功率在1 kW左右且具有低成本、高可靠性、高效率和高功率因数的家电领域用单管型感应电源[4-5]。该单管感应电源的参数优化设计存在以下不足:①没有优化开关频率,文中直接给出开关频率为21 kHz,较小的开关频率可以降低开关损耗但影响能量传输,开关频率应该受到系统各种条件相互限制而有一个最佳参数;②没有在设计前考虑原副边电感、电容的实际参数选择范围,以及电感、电容上的电流、电压大小等约束条件,往往设计完后发现参数不符合实际条件,需要重新设计多次才能得到一组优化参数[6-7];③没有从整体角度考虑系统各参数变化对最优目标的影响,如以电压增益最大为优化目标,先绘制原副边电感之比变化时的电压增益曲线,得到最优的原副边电感关系,再绘制互感变化时的电压增益曲线,得到最优的互感参数,实际上没有考虑两个待优参数之间的相互制约关系,所得到的最优参数很难全局最优[8-9]。
为克服以上不足,本文基于非线性规划思想,提出一种参数全局智能优化算法。将系统效率作为目标函数,以工作频率、原副边电感、电容为优化变量,以工作频率、原副边电感、电容及相关的电压、电流等作为约束条件,建立单管感应电能传输系统的非线性规划数学模型,采用智能优化算法进行非线性规划模型求解。为避免算法收敛于局部最优,设计了“遗传算法+模式搜索”的混合算法,即在遗传算法求得最优解的基础上,进一步采用模式搜索进行深度优化。该方法能将系统设计中的重要参数进行综合考虑,能涉及较多的参数且在优化中对各参数间的制约关系进行整体权衡,从全局角度对系统参数进行智能优化,可得到所有最优参数,避免了参数的逐次多次优化,减少了工作量。
1 电路模型分析
单管感应电能传输系统(SSIPT)基本电路模型如图1所示。Vd为直流电压源,可由交流电经整流滤波得到。谐振环节包括谐振松耦合变压器原边Lp、副边Ls、互感M及并联补偿电容原边Cp、副边Cs。功率开关管Q的控制电压用Ug表示,绪流保护二极管用D表示。为了简化分析,将负载等效成纯电阻Ro,负载上的电压用Uo表示。另外,为了优化时考虑更多实用参数,用UCp、ICp分别表示电容Cp的电压、电流,其他参数同理。
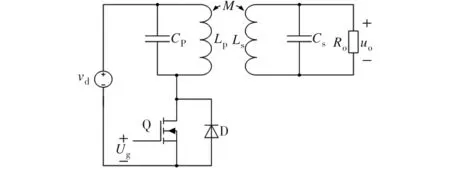
图1 SSIPT基本电路模型
为了方便使用基尔霍夫电流电压定律建立数学模型,采用松耦合变压器漏感模型建立基本电路的等效电路模型[10],如图2所示。图中,Ui为开关电路等效电压源,ZM、Zo分别为对应区域等效阻抗,Lpp、Lss分别代表原、副边漏感,图中标出了各支路的电压与电流符号。各参量的有效值一般指基波有效值。
忽略电源及线路内阻,Ui与UCp满足如下关系
UCp=Ui≈Vd
(1)
漏感Lpp、Lss满足下列关系
Lpp=Lp-M;Lss=Ls-M
(2)
等效阻抗Zo、ZM表达式整理为

参数优化中,假设Ui、Ro已知,f、Lp、Ls、Cp、Cs为待优化变量;总输入电流Ii,原边电感电流ILp、电压ULp,副边电感电流ILs、电压ULs,原边电容电压UCp、电流ICp,副边电容电压UCs、电流ICs,输出电压Uo设计时均需要考虑有效约束范围。根据KVL及KCL定律,可得
将式(1)~式(3)代入式(4)、式(5),各参量取模化简,整理得到电压、电流有效值分别为
式中:中间变量Δ、Λ、K的表达式分别为
Δ=M2-LpLs;Λ=Lp+ω2CsΔ;K=1-ω2LsCs
2 非线性规划模型
通过电路模型分析可知,SSIPT系统是典型的多参数、多约束非线性系统。非线性规划(NLP)是研究一个多元实函数在一组等式或不等式约束条件下的极值问题,是解决复杂非线性问题的一种全局优化方法。一般的NLP数学模型可表示为
式中:目标函数f(x)可以是单目标或多目标函数构成的向量;优化目标如果是最大化,通过数学方法转换成最小化;待优化变量x=(x1,x2,…,xl)为l维实向量,F表示可行域,S代表整个解空间;约束条件中有m个不等式约束gi(x)<0及n个等式约束hj(x)=0。
SSIPT系统参数设计时,应根据设计对象的体积、成本、实际条件等确定所选器件的额定参数范围,以使设计的系统具有最大可行性。SSIPT系统NLP建模过程如下。
(1)确定优化变量及解空间。令Vd、Ro、k为已知参数,Lp、Ls、Cp、Cs、f为待优化变量,则向量
x=(x1,x2,x3,x4,x5)=(Lp,Ls,Cp,Cs,f)
(9)
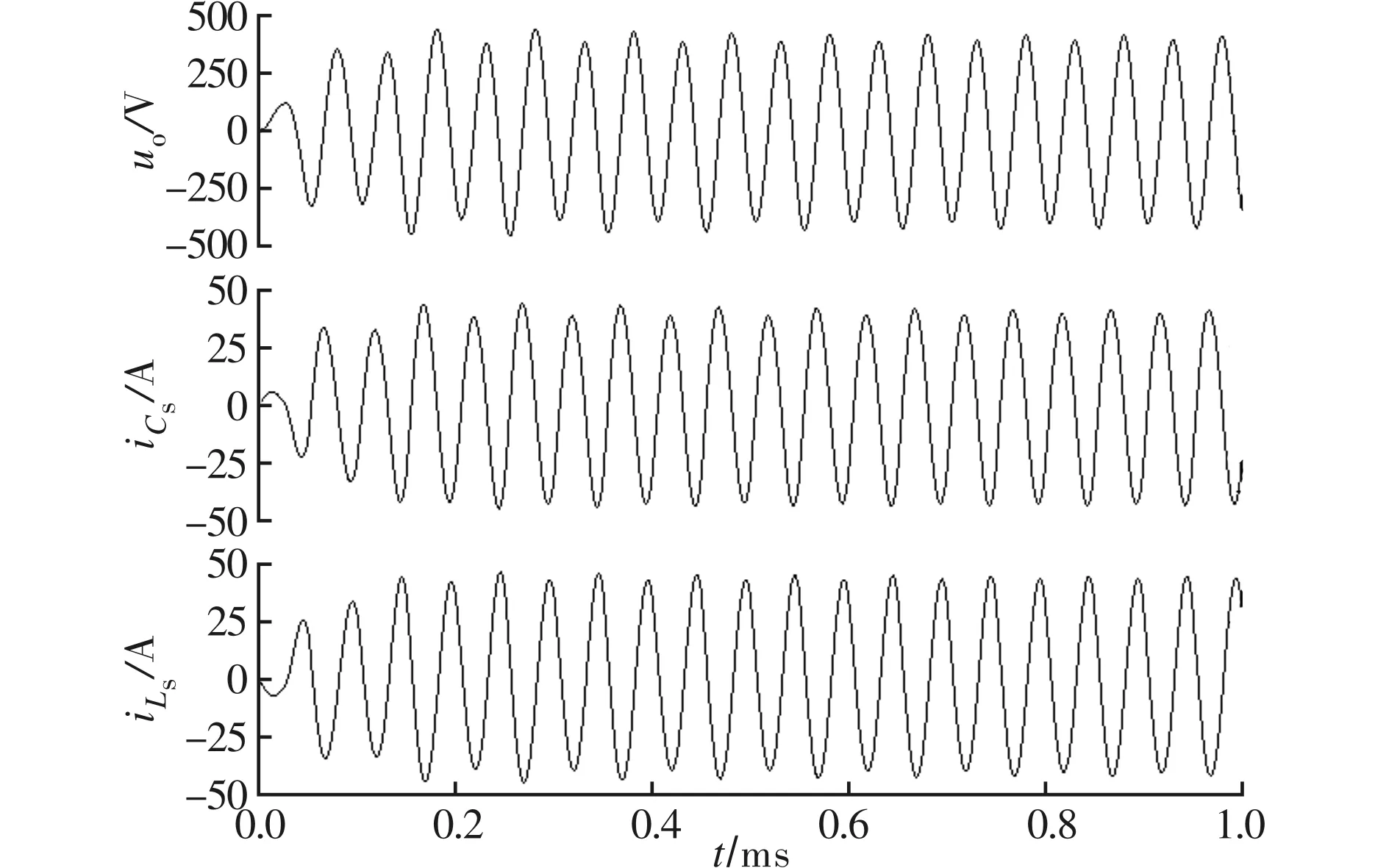
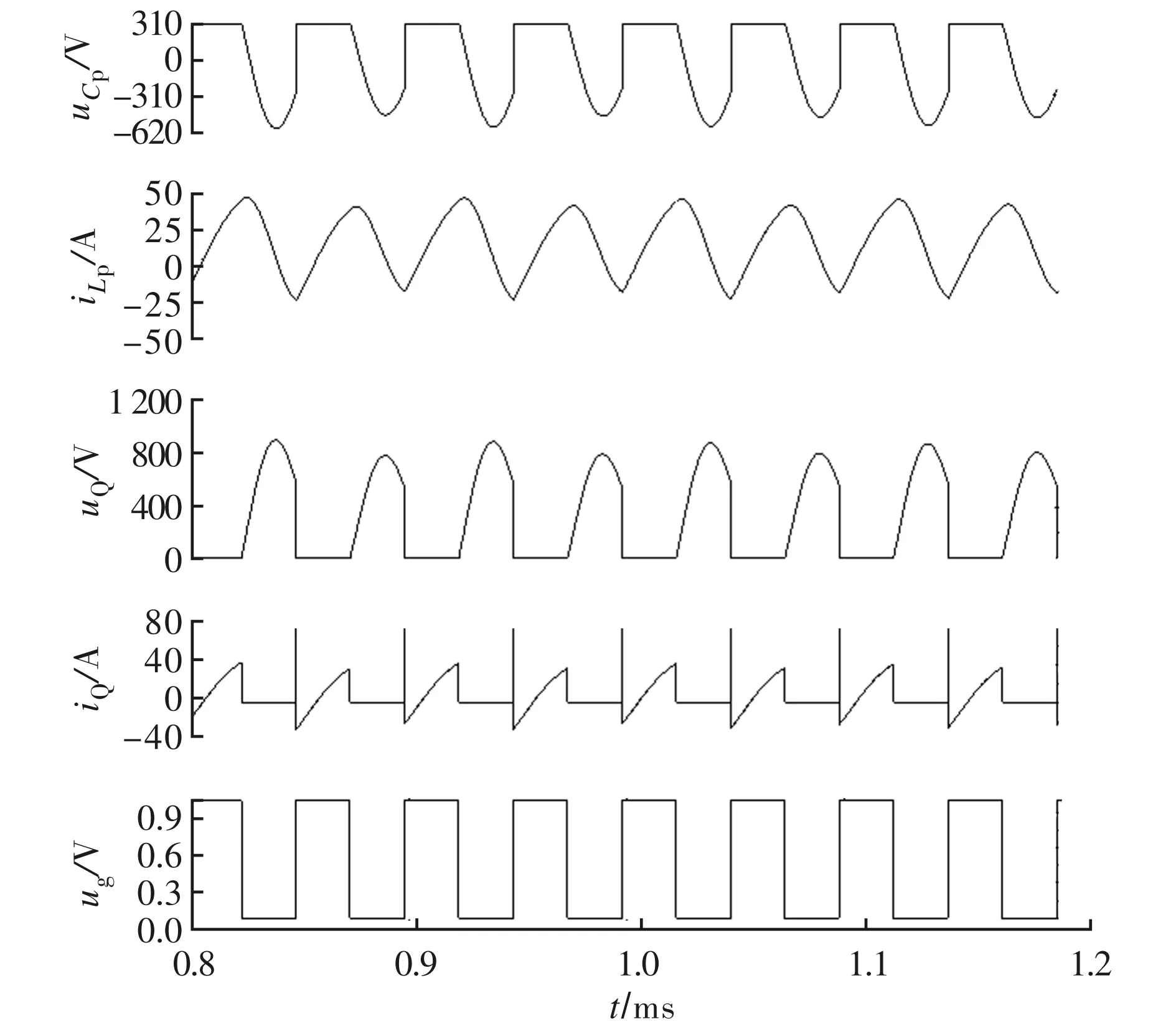
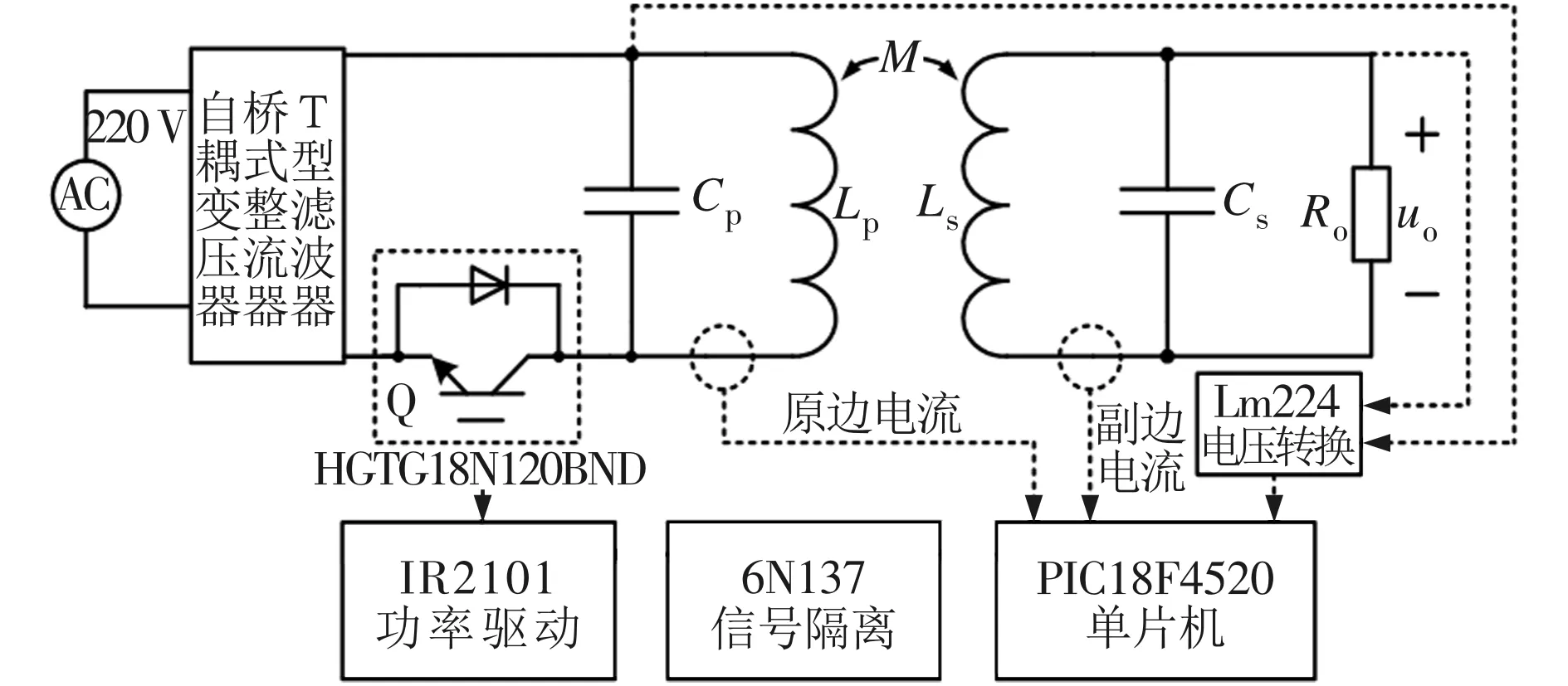
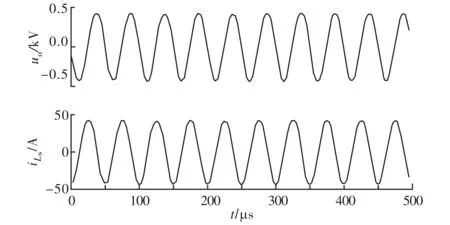
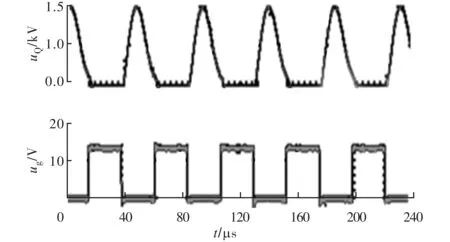
式中:Lpl (2)确定目标函数。以传输效率最高为优化目标,由式(6)、式(7)可得系统效率为 采用倒数方式将式(10)的目标函数转换成如式(8)所示的标准最小化模型,得 (3)确定约束函数。将各支路电压电流的范围作为系统参数间的约束关系,实际情况下各电感电容等都有额定的工作电压电流值,否则可能击穿线圈或烧毁电容,令ULpl、ULpu分别表示ULp的最小、最大值,其余参数类似,则不等式约束关系有 式中:Ui作为输入条件,在参数设计初应考虑电容电压的约束。根据式(8),将不等式约束转换成标准形式。以ULp为例,可得到两个标准形式为 g1(x)-ULpu<0; -g2(x)+ULpl<0 非线性规划问题根据目标约束函数的不同形式有多种求解方法,目前,解决复杂多约束NLP问题适应性较广的方法有模拟退火算法[11]、进化算法[12]、遗传算法(GA)[13]、粒子群算法[14]、蚁群算法[15]、模式搜索(PS)算法[16]等。算法优化中常将各种算法混合改进以达到全局最优。针对SSIPT系统的NLP问题,本文采用“遗传算法+模式搜索”(GAPS)形成一种新的混合算法。 遗传算法模拟生物进化,从一个包含很多初始点的种群出发,通过适应度函数选择最优种群,通过交叉、变异等方式使种群进化产生新个体[17]。模式搜索从一个初始点出发,以某种模式确定的动态网格在变量空间中不断地轮询最优解。遗传算法搜索的空间范围较大,有利于全局搜索[18];模式搜索适合于在一个点周围探索,局部搜索能力强。这两种算法可以优势互补形成一种既有较强全局搜索能力又能克服局部最优问题的新算法。GAPS混合算法主要思路是,先重复运行GA,进行T次全局优化,得到T个较优解,由于算法具有一定的不确定性,取T个解的算术平均值作为PS算法的初始点,最后通过PS算法进行局部搜索得到最终最优解。GAPS算法的具体过程如图3所示,需要说明以下几点。 图3 GAPS算法流程图 (1)GA种群混沌初始化。混沌是一种典型的非线性行为,具有随机性,并能在一定范围内按自身规律不重复地遍历所有参数[13]。本文利用Cat混沌序列发生器来产生分布更均匀的初始种群,Cat混沌模型为 式中:“mod1”表示取小数部分;xn、yn取(0,1)范围内非0.25、0.5、0.75等不动点的值。首先随机产生两个初始点x0、y0,利用式(13)迭代N/2次,得到N个混沌系数,最后对决策空间进行混沌扰动,形成规模为N的初始种群,扰动映射函数为 (2)适应度评价函数。利用增广拉格朗日算式,将目标函数及不等式约束合成一个适应度函数,再采用分级标定法对适应度函数进行处理形成新的评价函数,以增加进化种群的多样性。以式(8)的NLP标准形式为基础,不考虑等式约束,利用增广拉格朗日公式合成新的适应度函数为 (3)遗传选择操作。采用“锦标赛”方法,随机选择一定数量个体进行比较,挑出评价最高的一个,进行N次循环,得到种群规模为N的优良父种群。 (4)遗传进化操作。进化操作是解决如何产生子代种群使遗传搜索能够向前的问题,主要包括精英保留、交叉、变异操作方法,3种方法按一定比例相互配合共同产生子代种群。 精英保留方法确保当前种群评价值的个体直接继承为子代,避免进化中丢失优良基因个体,但保留的个体不能太多(文中保留2个),否则影响进化多样性。 交叉操作采用一种算术交叉方法,文中交叉操作贡献了除精英外种群个体的75%,剩余的25%子代由变异操作实现。 (5)子种群迁移。算法运行一定代数容易在小范围内迟滞不前,此时随机将当代种群分为大小相等的S个子种群,采用一种迁移方法,将每个子群中的最好个体迁移到另一个种群并替换掉最差个体。文中采用向前迁移,即第1个子群最优个体迁入第2个子群,如此类推,最后1个子群最优个体迁入第1个子群。 (6)遗传算法运行结束。单次GA终止的条件有最大迭代次数、算法停滞代数、适应度函数最大容限及约束函数的最大容限,任一条件满足算法均会退出。 由于算法结果的不确定性,需要多次运行得到T个GA运行最优值,T取6~10即可。 (7)模式搜索初始参数。假设运行T次,GA得到的最优解分别为x1、x2、…、xT,则PS算法初始解向量x′为 (8)模式搜索操作。采用广义模式搜索算法得到2倍优化变量个数的标准模式,标准模式与网格大小相乘再加上初始变量即得到新的轮询变量。通过计算所有轮询变量点上的适应度值,如果优于当前最优点,则表明轮询成功,最优点进行替换,否则表明轮询失败,最优点不变。当轮询成功,网格大小扩大2倍,否则缩小0.5倍。搜索结束条件是,最优解的提高精度达到规定容限(1×10-6)。 假设Vd=310 V、Ro=50 Ω、k=0.29,根据电感、电容及开关管的基本参数,给出待优化变量Lp、Ls、Cp、Cs、f的实际范围分别为[100,300]μH、[20,100]μH、[50,1 000]nF、[100,1 000]nF、[15 000,30 000]Hz。根据电路功率等级,电路结构及电缆、电容、电感等的电流及电压,给出电路各支路的电流、电压容限范围。为了简化设计仅考虑各参数最大值,即ULpu=600 V、ULsu=500 V、UCpu=800 V(由式(1)可知已满足条件)、UCsu=300 V、ILpu=30 A、ILsu=60 A、ICpu=30 A、ICsu=60 A、Iiu=30 A、Iou=20 A,Uol=200 V、Uou=300 V。通过设置输出电压范围来限定输出功率等级,以上参数可以根据设计需要进行调整,另外参数UCsu及Iou可以整合到Uou中去,最终得到5个优化变量、1个目标函数、9个非线性不等式约束的NLP模型。利用Matlab编写优化算法,得到的优化参数见表1、表2。 表1 优化变量相关参数 表2 约束条件相关参数 表1中前5个参数为优化变量,M为计算所得。表2为与9个约束不等式相关的参数,与给定条件相比较可知,所有非线性不等式约束均满足条件,理论系统优化目标效率达到98%。 为了检验算法性能,针对以上设计条件,与另外两种优化算法即双层混合遗传算法bi-level HGA[19]及自适应增强型模式搜索算法aEUS[20]进行比较,结果如图4所示。 图4 3种优化算法性能比较结果 bi-level HGA算法在120代停滞,aEUS算法在130代停滞且得到次优适应度值,本文GAPS算法在140代停滞且得到最优适应度值。因此,GAPS算法具有更好的优化搜索能力。 利用PLECS软件搭建电路模型对最优参数进行仿真验证。输出电压、副边电容电流及副边电感电流仿真波形如图5所示。 图5 uo、iCs及iLs的仿真波形 依据图5计算稳态时的有效值分别为Uo=287 V、ICs=28.6 A、ILs=30.4 A,仿真传输效率约为97%。仿真结果与表2中的理论值基本一致。 原边电容电压uCp、电感电流iLp、开关管电压uQ、电流iQ、开关管驱动方波ug的仿真波形如图6所示。在开关管导通时,uCp没有谐振到正向最大值,uQ较高,iQ有较大的冲击电流;开关管是在零电压条件实现了软关断。 图6 uCp、iLp、uQ、iQ及ug的仿真波形 由于开关管有较高的电压应力及较大的开通冲击电流,做实验易烧毁器件。参数设计还未能将软开关考虑进去,因为这种单管电路软开关条件公式极其复杂,难以得到解析解,一般结合经验采用仿真设计来调整参数实现软开关[4]。 根据相关文献,为了实现零电压开通,将Cp减小到285 nF(根据经验约为原值的0.55~0.6倍),得到的仿真波形如图7所示。 图7 uCp、iLp、uQ、iQ及ug的仿真波形(软开通) 在开关管导通时,uCp谐振到正向最大值,uQ为0,iQ有较小的反流,流过绪流二级管。Cp变化后,原边电流基本不变,而有效值Uo=295 V、ICs=29.6 A、ILs=30.8 A等参数有适当增加,所有参数的谐波含量减少,波形更接近正弦波。 通过实验电路进一步验证具有软开通特性的参数,如图8所示。开关管采用54 A/1 200 V的IGBT型号为HGTG18N120BND,驱动芯片采用IR2101,单片机PIC18F4520输出的弱电信号经过高速光耦6N137隔离,提高抗干扰能力。实验中以防过电压、过电流损坏系统,原副边线圈设有电流检测互感器采集电流,原副边电容电压采用运算放大器LM224进行电压信号转换,单片机进行综合检测控制,得到如图9、图10所示的实验波形。输入电压将市电经过变压整流滤波后得到稳定的直流电。 图8 实验电路示意图 图9 uo、iLs的实验波形(软开通) 图9给出输出电压uo及副边电感电流iLs波形,有效值Uo=283 V、ILs=29.7 A,副边波形接近正弦波,受磁芯结构及线路寄生参数影响,原边波形谐波含量较大,输出效率下降到约87%。图10给出开关管电压uQ及控制电压ug波形,IGBT开通时uo已经下降到0,实现了软开通;关断也是在零电压条件下进行的。 图10 uQ、ug的实验波形(软开通) 本文对单管无线电能传输系统进行数学建模,得到了系统设计所需关键参数的基本关系,建立了非线性规划数学模型,采用“遗传算法+模式搜索”的混合优化算法进行约束优化求解,并对全局优化参数进了仿真及实验验证。本文算法能综合考虑系统设计关键因素,一次性得出所有满足要求的最优化参数,克服了传统的一次仅考虑一个参数最优、难以兼顾参数全局最优的问题。本文所提出的GAPS算法具有较好的综合优化性能,可用于解决一般的NLP问题。由于研究有限,设计方法所得参数还未能完全实现软开关,对参数适当调节,得到了软开关参数并通过实验验证。3 混合优化算法


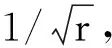
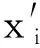
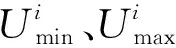
4 仿真及实验验证

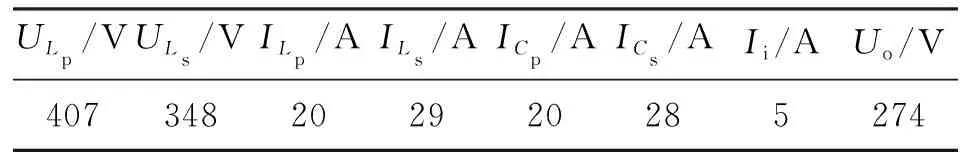


5 结 论
