基于Malmquist指数与面板模型的中国科技创新研究

崔俊富，陈金伟，邹一南

(1.南京航空航天大学 经济与管理学院，江苏 南京 210016；2.南京审计大学 经济与贸易学院，江苏 南京 211815；3.中共中央党校 经济学教研部，北京 100091)

一、问题提出

科技创新是人类进步发展的重要动力之一，很早就进入了经济学家的研究领域。熊彼特(Schumpeter，1934)认为，创新是建立一种新的生产函数，也就是把从来没有过的关于生产要素和生产条件的“新组合”引入生产体系；创新是内在要素，经济发展是来自内部自身创造性的关于经济生活的一种变动[1]。索洛(Solow，1956、1957)通过模型估计发现，1909—1949年技术进步贡献了大约87.5%的美国人均产出增长[2-3]。卢卡斯(Lucas，1988)研究发现，教育和干中学将进人力资本积累，进而促进经济增长[4]。中国学者的研究也验证了科技创新对中国经济增长的重要性。周绍森和胡德龙(2010)实证分析了中国1980—2007年各因素对经济增长的贡献份额，发现科技进步对经济增长贡献率为45.6%，并预测到2020年科技进步贡献率可达到60%左右[5]。李宏彬等(2009)运用动态面板系统广义矩估计方法研究，发现企业家创业和创新精神对经济增长有显著的正效应[6]。

从历史维度看，科技进步决定了一个国家、一个民族的长远发展。人类发展史存在一种世界时钟的概念，是指文明发达地区作为世界时间的基准，中国在人类文明的前中期曾长期是世界时钟的核心地区，但是近代以来，世界时钟逐渐向西方转移。林毅夫(2007)认为，自宋代以来中国未能及时实现向以科学与实验为基础的发明方式的转变，使得中国和西方的技术、经济差距迅速扩大[7]。麦迪森(Maddison，2009)测算了世界各个国家、地区公元元年至2008年的历史生产总值数据，结果显示：依靠广袤的国土和众多人口，中国的GDP占世界的比重曾经远远领先于世界上其他国家，占比基本维持在四分之一左右，但是工业革命之后，以英美为主的西方国家经济总量迅速扩张，逐渐超越了中国；改革开放之后，中国加大了科技投入，赶上了信息技术革命的末班车，经济飞速发展，1990年GDP占世界GDP的比重为7.8%，2008年达到了17.5%[8]。

科技创新在恒定的要素投入下，影响了产出，进而影响了一个国家、一个民族的进步。科技创新本身也必须考虑效率，在同等的物质、人力投入之下，高效率的国家、民族科技进步比较快，低效率的国家、民族科技进步比较慢，甚至有可能处于停滞状态。对科技创新进行效率评价，尤其是探究科技进步快慢的影响因素具有非常重要的意义。

二、基于Malmquist指数的中国科技创新测度

(一)中国科技创新Malmquist指数的构建

效率研究的开拓性贡献是索洛(Solow，1956、1957)做出的，在他构建的索洛模型中，物质资本K和人力资本L作为生产要素进入生产函数Y，A表示效率变化[2-4]：

Y=F(A，K，L)=AKαLβ

(1)

两边取对数，再对时间求导得：

(2)

索洛剩余非常容易理解，计算简单快捷，应用非常广泛。但是索洛剩余准确度不高，计算过于粗糙，很多问题得不到清晰的解释。为了克服索洛剩余的缺点，非参数前沿生产函数法随后得到发展。数据包络分析是非参数前沿生产函数法中的代表性方法，由查恩斯等(Charnes et al，1985)[9]提出，其核心思想是使用线性规划、随机规划、多目标规划等数学规划来对多个决策单元(decision making unit，DMU)相对有效性行进行评价[10]，数据包络分析提出后迅速在各个领域得到了广泛的应用。瑞典统计学家曼奎斯特(Malmquist，1953)在构建消费数量指数时提出了Malmquist指数[11]。基于数据包络分析方法，斐尔等(Fare et al，1994)对Malmquist指数做了分解[12]，将其分解为技术效率变动、技术进步和规模效率变动。雷等人(Ray et al，1997)认为斐尔等(1994)的分解是不正确的[13]，他们将Malmquist指数的分解修正为：

Moc(xt，yt，xt+1，yt+1)=TEΔ(xt，yt，xt+1，yt+1)×TΔ(xt，yt，xt+1，yt+1)×SΔ(xt，yt，xt+1，yt+1)

(3)

雷等人(1997)的研究结论得到了学术界的最终认可[14]。Malmquist指数分解式中，纯技术效率变化(pure technical efficiency change)由第一项TEΔ(xt，yt，xt+1，yt+1)测度，技术水平变化(technical change)由第二项TΔ(xt，yt，xt+1，yt+1)测度，规模效率变化(scale efficiency change)由第三项SΔ(xt，yt，xt+1，yt+1)测度，技术效率变化(technical efficiency change)由第一项与第三项的乘积TEΔ(xt，yt，xt+1，yt+1)×SΔ(xt，yt，xt+1，yt+1)测度[13-14]。生产可能性边界的移动由技术水平变化TΔ(xt，yt，xt+1，yt+1)来反映：当TΔ(xt，yt，xt+1，yt+1)=1时，表明技术水平没有变化，生产可能性边界没有移动；当TΔ(xt，yt，xt+1，yt+1)>1时，表明出现了技术水平提高；当TΔ(xt，yt，xt+1，yt+1)<1时，表明出现了技术水平下降。t时期到t+1时期的生产决策单元与生产可能性边界的距离变化由技术效率变化TEΔ(xt，yt，xt+1，yt+1)×SΔ(xt，yt，xt+1，yt+1)来反映：当技术效率变化TEΔ(xt，yt，xt+1，yt+1)×SΔ(xt，yt，xt+1，yt+1)=1时，表明距离不变，相对技术效率没有变化；当技术效率变化TEΔ(xt，yt，xt+1，yt+1)×SΔ(xt，yt，xt+1，yt+1)<1时，表明距离变大，相对技术效率降低了；当TEΔ(xt，yt，xt+1，yt+1)×SΔ(xt，yt，xt+1，yt+1)>1时，表明距离缩小，相对技术效率得到提高。本文选用产出主导型测量方法(output orientated measures)，选择国内固定资产投资作为内部物质资本因素，以外商投资衡量外来资本技术外溢影响，人口衡量人力资本的影响，专利申请数量作为产出变量。

(二)测度结果(见表1和表2)及讨论

在2004—2015年中，以Malmquist指数测度的科技创新全要素生产率在2005、2006、2008、2011、2012和2014年共6年处于上升趋势，在2004、2007、2009、2010、2013和2015年共6年处于下降趋势，总体上平均上升0.3%。整体来看，2000年之后中国创新效率不高与中国的人力资本优势消失紧密相关：受到人口政策的影响，改革开放后中国人口红利迅速到来，在一定人力投入之下，科技产出大幅度增加，但是进入21世纪之后，老龄化对中国科技创新的后续进步造成了持续性影响，科技创新活动不强，因此几乎所有年份的效率提升都不明显。2009和2010年连续下滑与经济危机紧密相关，各方面创新活动都受到一定影响。尤其值得注意的是2013年和2015年，中国科技创新全要素生产率处于下降趋势，2015年下降幅度达3.7%。

分组成来看，2004—2015年技术效率处于下降状态，平均下降0.1%，技术水平略微上升，平均上升0.4%，规模效率下降，平均下降0.1%，纯技术效率保持不变。技术水平略微上升0.4%，说明中国科技创新技术水平在上升，创新边界向好的方向移动，技术效率下降0.1%，说明实际科技创新与潜在创新边界的距离在扩大，科技创新过程中各要素并未得到更加合理有效的配置，科技创新活动更多地取决于创新要素的投入，而不是创新要素的有效整合，存在创新能力闲置的情况。分组成趋势变动与全要素生产率的情况相同，整体效率不高主要是中国人口红利消失影响，经济危机属于外部冲击因素，2013年和2015年各组成要素的下滑也应当引起足够的关注。

分区域来看，2004—2015年西部地区的科技创新全要素生产率最高，年均增长0.5%，其中技术效率保持不变，技术水平年均增长0.5%；中部地区的科技创新全要素生产率最低，年均下降0.1%，其中技术效率年均下降0.3%，技术水平年均增长0.2%；东部地区的科技创新全要素生产率居中，年均增长0.3%，其中技术效率年均下降0.1%，技术水平年均增长0.3%。分区域反映的情况与全国整体的情况大致相同，东部、中部、西部三大区域科技创新全要素生产率都不高，西部地区最高也仅为0.5%，中部地区还出现了下降趋势。三大区域的技术效率除西部地区保持不变之外，东部地区和中部地区均处于下降趋势，说明东部地区和中部地区存在创新能力闲置的情况。

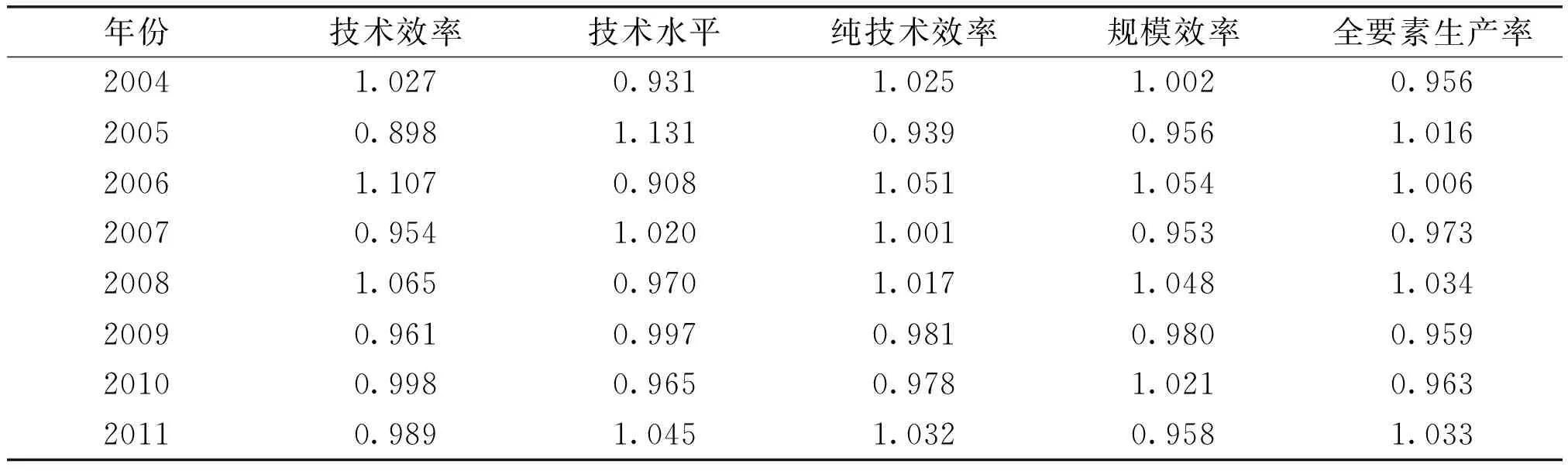
表1 2004—2015年全国Malmquist指数分年份情况

表1(续)

表2 2004—2015年分区域Malmquist指数情况

三、基于面板数据模型的中国科技创新模拟

Malmquist指数是效率测度方法，可以反映整体效率的变化，并对整体效率进行分解，而对于物质资本、人力资本等要素对科技创新的贡献必须使用别的方法进行测度。经典的线性计量经济学模型一般只利用二维数据，如时间序列数据模型或截面数据模型，这样会损失部分数据信息，只能反映数据情况的某一方面。将时间序列数据和截面数据结合起来便是面板数据，可以从三维角度研究变量之间的关系变化[15]。

(一)中国科技创新面板数据模型的构建

面板数据模型的一般形式为：

yit=αit+xitβit+μiti=1，2，…，N；t=1，2，…，T

(4)

其中，N表示截面成员个数，T表示每个截面成员的观测时期总数，参数αit表示模型的常数项，βit表示对应于解释变量xit的系数。根据是否有个体影响及结构变化以及个体影响的表现方式，面板数据模型可以分为不变系数模型、变截距模型和变系数模型[16]：

(5)

不变系数模型不考虑个体影响，将所有成员的数据简单堆积在一起进行建模；变截距模型使用不同的截距来表示个体影响；变系数模型使用不同的系数来表示个体影响及结构变化[17]。根据协方差分析检验结果，本文使用考虑个体影响的变截距模型来研究科技创新情况：

lnPatentit=αit+βlnFixit+γlnFDIit+ηlnHumanit+μiti=1，2，…，N；t=1，2，…，T

(6)

其中，Patentit为专利，衡量科技创新产出；αit为截距项，衡量科技创新的自发影响；Fixit为国内固定资产投资，衡量内部物质资本影响；FDIit为外商投资，衡量外来资本技术外溢影响；Humanit为人口，衡量人力资本的影响，其中，产出变量和投入变量的选取与Malmquist指数的产出变量和投入变量的选取相同。β、γ和η为回归系数，分别表示固定资产投资、外来投资和人口的影响程度。当β、γ和η为正数时，说明自变量和因变量是正相关关系，随着投入变量的增加，科技创新产出增大；当β、γ和η为负数时，说明自变量和因变量是负相关关系，随着投入变量的增加，科技创新产出减小。本模型的自变量和因变量都是对数形式，回归系数β、γ和η即为产出Patentit相对于投入Fixit、FDIit和Humanit的弹性，分别表示内资科技产出弹性、外资科技产出弹性和人力科技产出弹性。

(二)模拟结果及讨论

1.全国情况

lnPatent=-2.11+0.84lnFix+0.27lnFDI+0.27lnHuman

(7)

(-1.86*)(22.8***) (4.71***)(1.84*)

R2=0.97F=402***

其中，*、**、***分别代表0.1、0.05、0.01显著性水平，后文同。全国模型的基本性质比较优良，决定系数达到了0.97，说明自变量可以解释大部分因变量，所有自变量均通过了显著性水平为0.1的显著性检验。整体来看，内部资本对全国科技创新的影响最大，内资科技产出弹性达到了0.84，说明内部资本投入增加1%，科技创新产出增加0.84%；外来资本溢出与人力资本对全国科技创新的影响相同，外资科技产出弹性和人力科技产出弹性均为0.27，说明外来资本、人力资本增加1%，科技创新产出增加0.27%。

2.东部地区情况

lnPatent=-15.62+0.79lnFix+0.26lnFDI+2.01lnHuman

(8)

(-4.32***)(13.34***)(2.87**) (4.15***)

R2=0.96F=281***

东部地区模型的基本性质也比较优良，决定系数达到了0.96，说明自变量可以解释大部分因变量，所有自变量均通过了显著性水平为0.05的显著性检验。整体来看，人力资本对东部地区科技创新的影响最大，人力科技产出弹性达到了2.01，说明人力资本投入增加1%，科技创新产出增加2.01%；外来资本对东部地区科技创新的影响最小，外资科技产出弹性为0.26，说明外来资本增加1%，科技创新产出增加0.26%；内部资本对东部地区科技创新的影响居中，内资科技创新产出弹性为0.79，说明内部资本投入增加1%，科技创新产出增加0.79%。

3.中部地区情况

lnPatent=29.13+0.74lnFix+0.53lnFDI-3.51lnHuman

(9)

(1.98**) (8.72***) (3.48***)(-2.01**)

R2=0.92F=122***

中部地区模型的基本性质也比较优良，决定系数达到了0.92，说明自变量可以解释大部分因变量，所有自变量均通过了显著性水平为0.05的显著性检验。整体来看，内部资本对中部科技创新的影响最大，内资科技产出弹性为0.74，说明内部资本投入增加1%，科技创新产出增加0.74%；人力资本对东部地区科技创新的影响最小，人力科技产出弹性为-3.51，说明人力资本投入增加1%，科技创新产出减少3.51%；外来资本对东部地区科技创新的影响居中，外资科技产出弹性为0.53，说明外来资本增加1%，科技创新产出增加0.53%。

4.西部地区情况

lnPatent=-0.43+0.85lnFix+0.18lnFDI+0.07lnHuman

(10)

(-0.44) (16.92***)(2.49**)(0.55)

R2=0.97F=344***

西部地区模型的基本性质一般，决定系数达到了0.97，说明自变量可以解释大部分因变量，内部资本和外来资本通过了显著性水平为0.05的显著性检验，但是人力资本未通过显著性水平为0.1的显著性检验。整体来看，内部资本对中部科技创新的影响最大，内资科技产出弹性为0.85，说明内部资本投入增加1%，科技创新产出增加0.85%；人力资本对东部地区科技创新的影响最小，人力科技产出弹性为0.07，说明人力资本投入增加1%，科技创新产出增加0.07%；外来资本对东部地区科技创新的影响居中，外资科技产出弹性为0.18，说明外来资本增加1%，科技创新产出增加0.18%。

比较来看，中部地区的自发影响最大，西部地区居中，东部地区最小。内部资本要素方面，西部地区科技创新对内部物质资本变化的响应最大，中部地区科技创新对内部物质资本变化的响应最小，东部地区科技创新对内部物质资本变化的响应居中。从外来资本要素来看，中部地区科技创新对外来资本变化的响应最大，西部地区科技创新对外来资本变化的响应最小，东部地区科技创新对外来资本变化的响应居中。人力资本要素方面，东部地区科技创新对人力资本变化的响应最大，中部地区科技创新对人力资本变化的响应最小，西部地区科技创新对人力资本变化的响应居中。

整体来看，面板模型估计的分区域创新情况与Malmquist指数测算的分区域创新情况是基本一致的。中部地区科技创新情况最差，尽管自发影响最大，但是人力科技产出弹性为负值，说明人力资本投入对科技创新是负向拉动，并且负向拉动效应比较大。东部地区科技创新情况居中，内部资本、外来资本、人力资本对科技创新都是正向拉动，但是自发影响为负向拉动，并且负向拉动较大。西部地区科技创新相对最好，内部资本、外来资本、人力资本都是正向拉动，并且自发影响负向拉动较小，但是西部地区的人力资本变量未通过显著性检验，说明在西部地区的科技创新过程中，人力资本并未发挥出应有的作用。综合分析，全国、东部、中部、西部的科技创新情况都不是十分乐观，中国整体的科技创新效率仍然有比较大的上升空间，需要对投入要素、组织方式进行改善。

四、结语

本文使用数据包络分析和面板数据模型对中国的科技创新情况进行了测度。数据包络分析表明，在2004—2015年，中国科技进步全要素生产率呈现了增长趋势，但是平均速度仅为0.3%，其中，西部地区最高，中部地区最低。较低的增长速度表明在科技创新过程中各要素并未得到更加合理有效的配置，科技创新活动更多地取决于创新要素的投入，而不是创新要素的有效整合。通过面板数据模型分析发现，物质资本、人力资本在科技创新过程中发挥了不同的作用，全国来看，内部资本对中国科技创新的影响最大，外来资本和人力资本的影响较小。分区域来看，不同投入要素在不同区域科技创新过程中也产生了不同的影响，例如，在内部资本影响方面，西部地区科技创新对物质资本变化的响应最大，中部地区科技创新对物质资本变化的响应最小。值得注意的是，人力资本要素方面，中部地区科技创新对人力资本变化的响应为负，而且西部地区科技创新对人力资本变化的响应比较弱，说明在中部地区和西部地区科技创新过程中，人力资本的作用有待进一步挖掘。作为世界上最大的发展中国家，中国保持经济的平稳较快增长仍然是近一段时期最大的任务[18-19]。科技创新是人类进步发展的重要动力，保持较高的科技进步速度是中国经济保持平稳较快增长，实现中华民族伟大复兴的战略支撑。根据上述结论，本文提出以下政策建议：

第一，加强物质资本积累。要加大财政投入力度，发挥财政资金的先导作用，对重点领域、重点行业加大财政资金投入；要制定政策措施，引导社会资金进入科技创新领域，激发社会力量的积极性、主动性和创造性来促进科技创新；要大力推进重大科技专项，兴建并发展一批具有国际影响力的科研实验室。

第二，加强人力资本积累。科技创新的第一要素是人力资本，要采取有效措施加强科技创新人才队伍建设。一方面，大力发展科技创新教育，尤其是科技类和工程类教育，培育更多的科技创新人才。另一方面，推动体制机制创新，为人才从事科技创新工作提供良好的市场环境。

第三，继续扩大开放。1978年以来，外来生产要素的进入，特别是先进生产技术的涌入极大地推动了中国科技进步。中国未来的科技发展同样离不开与先进国家的联系沟通，应该锐意推动改革，进一步扩大科技创新领域的开放，形成科技创新的双向交流机制，推动中国科技创新跨越式发展。

第四，统筹协调区域科技创新发展。中国各地区的科技进步情况千差万别，影响了各地区的经济社会发展速度。未来应当针对不同地区制定差异化的科技创新政策，促进各地区科技创新的协调平稳发展。