选择性激光熔化成形温度场模拟与分析

池 敏 钱 波 魏青松 张剑睿

(①华东理工大学机械与动力工程学院，上海 200237；②华中科技大学材料科学与工程学院，湖北 武汉 430074)

选择性激光熔化技术(selected laser melting，SLM)是一种金属件直接成形的方法，该技术是利用金属粉末在激光束的热作用下完全熔化、经冷却凝固而成型的一种技术。在高激光能量密度作用下，金属粉末完全熔化，经散热冷却后可实现与固体金属冶金焊合成型。SLM技术正是通过此过程，层层累积成型出三维实体的快速成型技术。

根据成型件三维CAD模型的分层切片信息，扫描系统(振镜)控制激光束作用于待成型区域内的粉末。一层扫描完毕后，活塞缸内的活塞会下降一个层厚的距离；接着送粉系统输送一定量的粉末，铺粉辊铺展一层厚的粉末沉积于已成型层之上。然后，重复上述2个成型过程，直至所有三维CAD模型的切片层全部扫描完毕。这样，三维CAD模型通过逐层累积方式直接成型金属零件。最后，活塞上推，从成型装备中取出零件。至此，SLM金属粉末直接成型金属零件的全部过程结束。

温度是SLM整个过程的关键参数之一，激光束周围的温度高于金属粉末的熔点，离激光束中心距离越远的地方，温度降低的越快，就会产生较大的温度梯度。而较大的温度梯度则会引起热变形以及热应力、应变，这些都将影响着零件的尺寸和成形精度，甚至产生裂纹等。

在SLM零件加工过程中，激光功率、扫描速率、扫描间距、扫描方式等工艺参数影响着成形过程中的温度场、熔池尺寸。因此，对成形过程的温度场、熔池的有限元模拟可以作为优化成形工艺参数的工具[1-3]。

Robertsetal[4]等提出了一个制造Ti6Al4V零件的三维热模型，考虑了基于温度的热物特性，有利于提高计算精度。这个模型包括多层，因为连续层的热相互作用影响了温度梯度，而温度梯度决定了热传递和热应力发展机制。该研究预测了加工过程中的瞬态分布，研究结果发现激光区域经历了快速的热循环，伴随相应的应力循环。

Qimin Shi[5]等建立了一个TiC/Inconel718粉末系统的三维SLM模型，该模型用来研究在SLM中激光功率和扫描速率对热行为和熔融/凝固机制的影响。研究表明：当激光功率从75 W增加到150 W时，熔池的最大温度梯度有一个明显的增长，然而，扫描速率的变化对其影响基本是可忽略的。同时，150 W的激光功率与100 mm/s的扫描速率的结合可以实现轨迹与轨迹，层与层之间较好的粘接。

DAI[6]等建立了多种材料激光致密化激光快速成形方法的有限元分析模型，考察了加工过程中瞬态温度场、瞬态应力场，模型中考虑了随温度及孔隙率变化的热传导、热辐射条件和随温度变化的热对流条件，还采用折算的办法考虑了粉末到实体的转变中热导率的变化，但仅仅考虑了孔隙率为最大的粉末状态和孔隙率接近于零的近实体状态，没有考虑在大温度范围(从室温到材料熔点)内的热导率变化规律。

沈显峰[7]等利用MSC.Marc软件，建立了一个SLS过程的温度场有限元分析模型，在模型中考虑了粉末-实体转化过程中不同单元导热率等物理性质随温度变化的非线性变化规律，采用了不同载荷步之间转换单元材料物理性质的方法，结果表明：在烧结开始时光斑中心附近具有极大的温度梯度，与实验结果相符合。

胡增荣[8]等基于ABAQUS 平台建立了移动热源作用下的三维瞬态金属粉末激光多道烧结温度场的有限元模型，考虑了相变潜热的影响，以水雾化铁粉为烧结材料进行了模拟，研究表明：较低的扫描速度会使温度大幅上升, 烧结深度加大, 可以获得更大的以光斑为中心的液相区域。模拟时，在第一道起始处产生较大的温度梯度。

针对现有模型中存在不足：未充分考虑熔融过程材料属性随温度的变化，多层多轨道成形中未按实际加工预留铺粉时间等。本文通过使用有限元分析软件ABAQUS来综合性的模拟选择性激光熔融成形过程，主要的研究内容有：建立一个温度/位移耦合的三维多层有限元模型，通过子程序的设置解决现有模型的不足，并验证模型的正确性；模拟分析激光功率和扫描速率对热行为和熔池结构形成机制以及层与层之间粘结效果的影响。

1 有限元建模理论

1.1 SLM物理描述

图1中所示为SLM技术中，激光辐射与粉末之间的内部区域示意图。粉床上表面吸收激光能量熔融形成熔池，在这个过程中金属材料经历着从粉末颗粒到液体再到固体的状态变化和相变，主要的热传递机制包括激光与粉床之间的辐射，金属基板与粉末颗粒、粉末颗粒与粉末颗粒之间的热传导以及粉床表面与周围环境的热对流和热辐射。

1.2 控制方程

SLM的温度场分析过程属于经典的非线性瞬态的三维热传导问题，满足能量守恒定理和傅里叶定理，热传导微分方程[9]可表示为：

(1)

式中：ρ表示材料密度，kg/m3；c表示材料比热容，J/(kg·K)；T表示材料瞬态温度，K；t表示时间，s；kx、ky、kz分别表示材料在x、y、z三个方向上的热传导率，W/(m·K)，由于本文假设材料为各向同性，所以kx=ky=kz=k；Q表示相变潜热相，J/mm3。

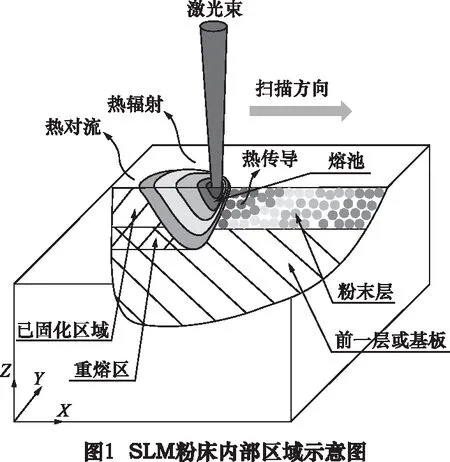
1.3 初始条件与边界条件的确定

热源加载前，假设粉床的初始温度是室温293 K，则温度场初始条件可以由式(2)表达：

T(x,y,z)t=0=T0=293 K

(2)

假设基板无热量损失，其温度为T0。在SLM整个过程中，粉床的上表面与周围的环境存在着热对流和热辐射，温度场的边界条件[10]可表示为：

(3)

式中:σ为Stefan-Boltzmann常数，约为5.67×10-8W/(m2·K4)；εθ表示实际物体的有效辐射率(黑度)，取0.8；Ts为环境温度，K；Te为换热介质温度，K；h为对流换热系数，取12 W/(m2·K)。

1.4 移动热源的加载

在SLM过程中，由于SLM是逐层加工，层厚比较小，激光的穿透比较小，所以采用高斯面热源[11]来模拟激光能量(如图2)，公式如下：

(4)

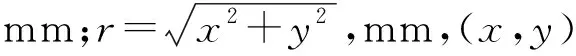
(5)

ABAQUS中热源的移动是通过调用用户子程序DFLUX来实现。实现在不同时刻不同位置加载热源。在热源的移动加载过程中，ABAQUS可以实现热源在不同粉末层上的加载：首先将所有的粉末层单元都去除掉，在热源开始加载前，激活第一层粉末，模拟真实加工过程的铺粉，第一层制造完成后再依次激活下一层的粉末单元，直到整个成形过程的完成。

1.5 相变潜热的处理

SLM成型过程一直伴随着粉末材料的熔融、凝固等复杂的过程，材料在熔融和凝固的过程中会发生相变，相变会伴随着潜热的释放与吸收，本文采用等效比热容的方法，对相变区域的材料比热容Ce进行了修正[13]，如公式(6)：

(6)

式中：C为材料的真实比热容，J/(kg·K)；L为潜热，J/mm3；TL为液相线温度，K；TS为固相线温度，K。

不锈钢实体的比热容是随温度变化的，将比热容C的离散数据进行拟合得到：

C=2.266 8×10-7T3-3.92×10-4T2+
0.301 437 51T+410.648

(7)

1.6 材料导热率的确定

在激光熔融过程中，粉末材料吸收能量熔融并快速凝固为实体，这样造成了粉床中材料属性的变化，由于实体的导热率远远大于粉末的导热率，因此要对粉末状态和实体状态的材料属性加以区分，以提高模拟的精确。

由Sih模型可将粉末状态的有效导热率[14]定义为：

(8)

式中：ke为粉末有效导热率，W/(m·K)；kf为空气热传导率，W/(m·K)；ε为孔隙率；ks为实体导热率，W/(m·K)；kr=4FσT2D为由辐射引起的导热系数，W/(m·K)；F为表观系数，为1/3；D为粉末颗粒直径，mm。本文不锈钢316L粉末的粒径为35 μm。

对不锈钢316L实体导热率以及空气热传导率的离散数据分别拟合得到公式：

ks=7.129×10-9T3-1.168×10-5T2+0.014 6T
+9.589 7
kf=1.712 23×10-9T3-5.932×10-6T2+0.011 33T
-0.272 6

(9)

假设当材料温度处于固相线和熔点温度之间，熔融粉末导热率线性的变化到实体的导热率，则任一时刻的导热率可表示为：

k=ke(1-φ)+ksφ

(10)

式中：k为材料任一时刻的导热率，W/(m·K)；φ为实体所占比例；ke为粉末有效导热率，W/(m·K)；ks为实体导热率，W/(m·K)。本文采用UMATHT子程序来定义热传递过程中材料的热本构行为，当材料发生熔融时，材料属性由粉末状态永久地改变为实体状态。

2 模拟内容

本文所建立的模型如图3所示，粉床尺寸为1.75×0.35×0.105 mm，共三层。如图3a，粉末层厚为0.035 mm，基板尺寸为2×0.5×0.2 mm，模型使用六面体网格划分，粉床网格尺寸为0.035×0.035×0.017 5 mm，基板顶部过渡网格尺寸为0.05×0.05×0.017 5 mm，底部网格尺寸为0.05×0.05×0.05 mm。在三层粉末层上共选取5个点P1～P5，在第二层粉末层上沿着扫描路径选取S-S路径，如图3b，研究不同时刻不同位置的温度分布。

模拟的工艺参数采用与实际工艺参数相同的值，如表1。模拟有3个加热分析步，同时在每一层粉末扫描后设置了一个5 ms的冷却分析步(如表2所示)，一是为了模拟真实的实验铺粉过程，二是为了散热，防止刚扫描过的粉床表面温度太高导致新铺的粉末层还未扫描就出现部分区域熔融的现象，维持熔池温度和尺寸的稳定，来提高制件的质量。

表1 模拟参数

参数数值粉末层厚d/μm35光斑直径D/μm100环境温度T0/K293激光功率P/W25,75,125,175扫描速率v/(mm/s)300,500,700,900

表2 分析步设置

分析步内容作用Step0去除所有粉末层10-3 ms放置基板Step-heat1激光扫描第一层粉末铺第一层粉末,并加载热源Step-cool1铺粉等待5 ms模拟真实铺粉过程,防止粉床过热Step-heat2激光扫描第二层粉末铺第二层粉末,并加载热源Step-cool2铺粉等待5 ms模拟真实铺粉过程,防止粉床过热Step-heat3激光扫描第三层粉末铺第三层粉末,并加载热源Step-cool3冷却10 s冷却

3 分析讨论

3.1 单层模型验证

为了验证所建立模型的正确性，本文做了一个对比研究。将模拟结果与文献[15]中的研究结果进行了比较，文献中通过观测实验件的表面形貌与模拟的温度结果相对比，验证了其模型的正确性。单层模型采用已发表文献中的工艺参数：P=100 W，v=40 mm/s，光斑半径r=0.3 mm，在单层单轨道扫描中，文献中得到的模型中心节点最高温度为2 272 K，本文所做的模型中心最高温度大约为2 160 K(如图4)，温度稍有不同的原因是本文模型中基板是实体材料，实体导热率比粉末导热率高很多，而文献中所建立的模型只有粉末材料，温度故而会低一些。由此可见，本文所建立的模型是正确的。

3.2 多层模型温度分布特征

表3是激光参数为75 W，500 mm/s，激光束分别扫描到P1～P5点时的粉床表面以及熔池最大宽度横截面温度分布图，箭头表示激光移动的方向,三层模拟的激光束移动方向相同。图中等温线表示的是不锈钢316L的熔化温度，等温线内部的温度高于熔点，形成一个小的熔池。熔池顶部表面的等温曲线与椭圆线相似，前部分的椭圆比后端更密集。激光束移动到P1点时，材料熔融形成的熔池最高温度是3 029 K，熔池的三维尺寸大约为56(长)μm×87.5(宽)μm×15.75(高)μm；激光束移动到P2点时，熔池最高温度是3 356 K，熔池尺寸为297.5μm×131.25μm×42μm；激光束移动到P3点时，熔池最高温度是3 505 K，熔池尺寸为276.5μm×132.5μm×43.75μm；当激光束移动到P4点时，熔池最高温度是3 363 K，熔池尺寸为574 μm×133 μm×54.25 μm；当激光束移动到P5点，熔池最高温度是3 369 K，熔池尺寸为777 μm×134.8 μm×68.25 μm。由于温度的热累积效应，温度逐渐升高，且熔池尺寸逐渐增大。

图5是P1～P5五个点温度随时间变化曲线图，同一层上的点有着类似的温度变化趋势，P1，P2，P3，P4，P5点最高温度值分别为2 990.1 K、3 451.67 K、3 504.6 K、3 543.3 K、3 543.9 K。由表3和图5 中的温度分布可以发现，由于热传导和热累积的原因，当激光束移动到点P1、P2、P4、P3、P5时的温度并不是该点的历史最高温度，历史最高温度出现的时间往往会滞后一点。此外，点P4与P2相比，最高温度增加了0.04%，熔池的长、宽、高分别增加了93%、1.33%、29%，点P5与P4相比，最高温度增加了0.02%，熔池的长、宽、高分别增加了35%、1.35%、25.8%。可以看出，温度增加的不是很明显，这是因为在每一次扫描完成后有一个5 ms的冷却时间，减小了热累积作用。同时，由于热传导，后一层热源的扫描使得前一层上点的温度达到二次峰值。

表3 熔池上表面及截面形态

熔池上表面形态熔池截面形态第一层整体模型P1点P2点P3点P4点P5点

在SLM工艺过程中，随着逐层制造，模拟结果所示的平均温度和熔池尺寸逐渐增加。这主要是由于之前粉末层的加工对接下来要加工的区域有热积累的影响。此外，由于热传递效应比粉床表面与周围环境的热对流和热辐射引起的热损失大很多，所以这也是导致熔池温度和尺寸增加的原因。

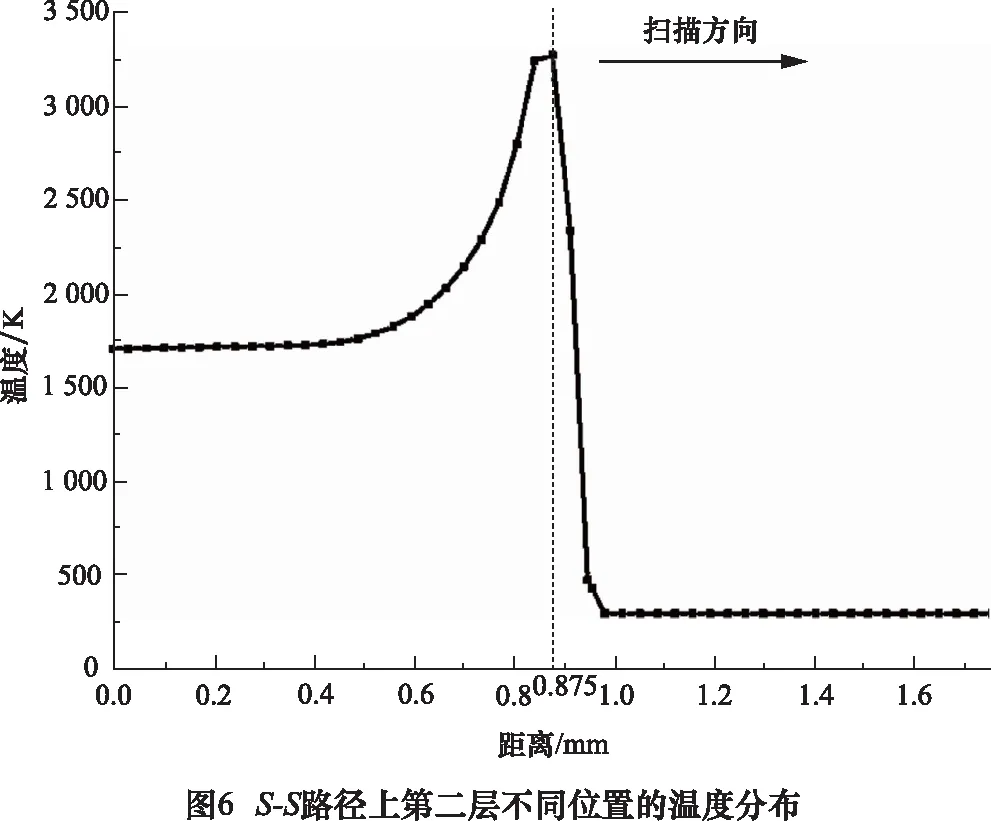
0.875 mm是S-S路径的中点，当激光束扫描到0.875 mm处时，第二层粉床S-S路径上不同位置的温度分布如图6所示，结合表3熔池表面形貌可以看出，沿着激光扫描方向，熔池前端的温度梯度比熔池后端的温度梯度大很多，这主要是由于材料状态变化引起了导热率的变化，熔池前端粉末的导热率比熔池后端实体的导热率小很多，造成熔池前端温度梯度较大。

3.2.1 不同工艺参数下的温度分布

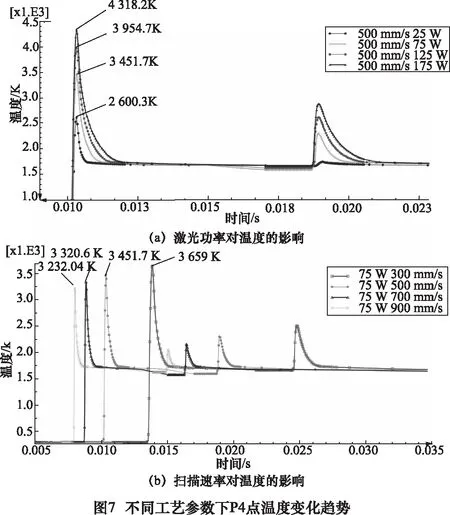
图7是不同的工艺参数下，P4点温度随时间的变化图，曲线表明加热冷却的过程发生在十分之几毫秒之内，可以认为激光热源的辐射点受到快速的热循环，而快速的热循环与热应力的改变有关。图7a温度曲线图表明随着激光功率的增大，熔池温度也随之升高；图7b温度曲线图表明随着激光扫描速率的增大，熔池温度随之降低，但是激光扫描速率对熔池温度的影响没有激光功率对其影响大。

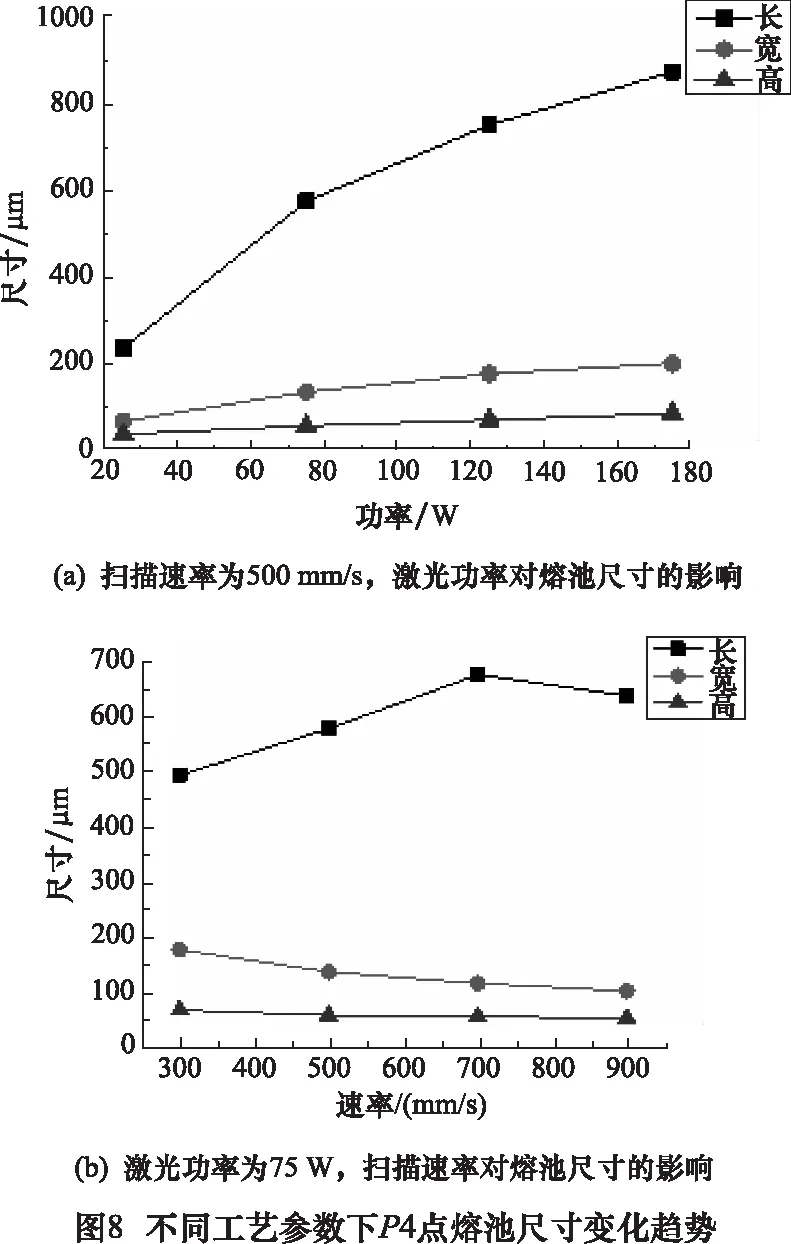
3.2.2 不同工艺参数下的熔池尺寸

图8是激光扫描到P4点时在不同工艺参数下，熔池的长、宽、高尺寸随时间的变化图。如图8a所示，当激光功率从25 W增加到175 W时，熔池的尺寸也随之增加，如长度从234.5 μm增加到873.25 μm，宽从98 μm增加到199.5 μm，熔池高从35 μm增加到83.13 μm。然而当激光扫描速率增加时，熔池的宽和高是减小的(如图8b)。扫描速率从300 mm/s增加到900 mm/s时，熔池的宽从173.25 μm减小到98 μm，熔池高从63.88 μm减小到49 μm。然而熔池的长度先增加后减少，这是由于扫描速率从300 mm/s增加到700 mm/s时，输入的能量较大，粉床表面由热对流和热辐射产生的热损失相比较小，熔池尺寸逐渐增加，当扫描速率从700 mm/s增加到900 mm/s时，激光束移动速率较快，输入粉床能量相对减少，所以熔池的长度减小。

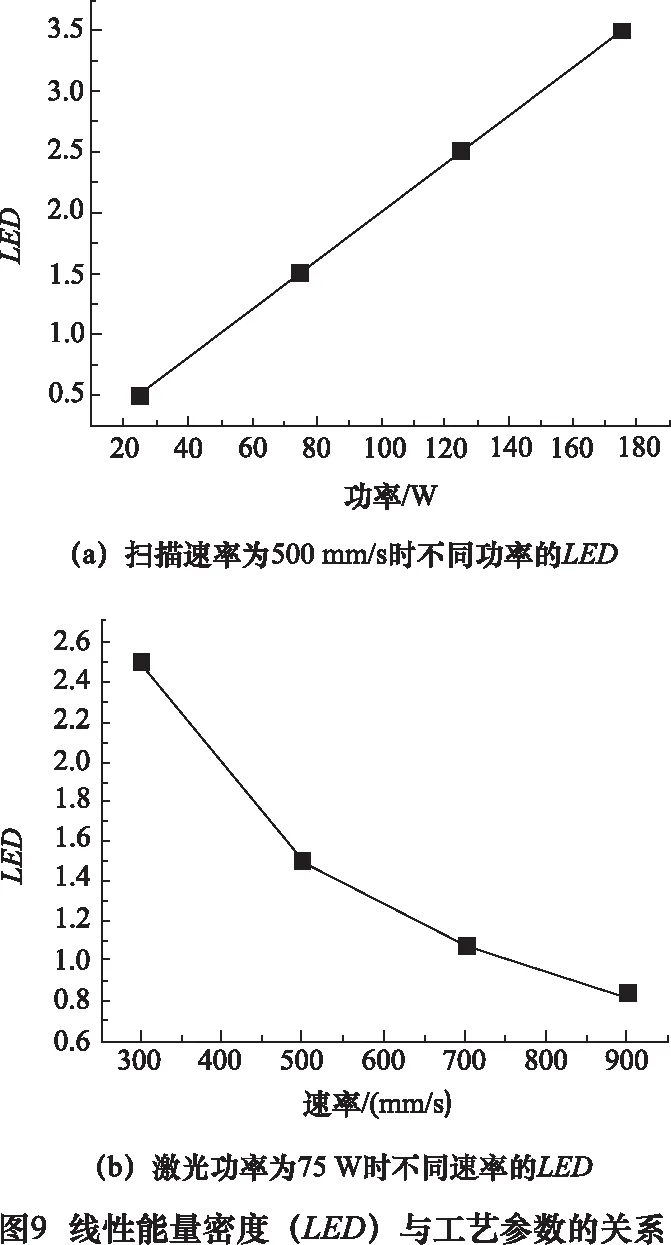
选择性激光熔融是一种激光扫描多轨迹多层的加工技术，所以相邻轨迹和相邻层之间的粘接作用对所制造的零件精度以及密度有着重要的影响。为了进一步研究激光功率与扫描速率整体对SLM成形过程中粉床温度分布的影响，引入线性能量密度(line energy density,LED)[16]的概念,即:

(11)

式中：LED为线性能量密度，J/cm；P为激光功率，W；V为扫描速率，mm/s。

两组模拟的能量密度如图9所示，结合模拟结果可知，能量密度的范围在1.5～2.5 J/cm(P=75 W时v=300～500 mm/s或v=500 mm/s时，P=75～125 W)时，熔池温度、三维尺寸比较合适，成形的零件质量较好；能量密度较小时(如P= 75 W时v>500 mm/s或v=500 mm/s时，P=25 W)，熔池温度低，熔池尺寸太小，层与层之间有未熔融颗粒，粘接效果不好；能量密度较大时(如P=75 W时v<300 mm/s或v=500 mm/s时，P=175 W)，熔池温度太高，容易造成材料的气化导致成形件质量不好，同时熔池尺寸太大，会导致成形件的应力累积。

4 结语

本文建立了一个三维温度/位移耦合有限元模型，考虑了基于温度的热物性参数、铺粉的冷却时间、热传导、对流/辐射散热、相变潜热以及材料状态的改变，主要研究了工艺参数对温度场中温度分布和熔池尺寸变化的影响，可以总结为以下几点：

(1)在多层模拟中，后一层比前一层相同位置的最高温度高，但增加的不是很明显，主要是因为在每一层热源加载完毕后设置了5 ms的冷却时间减少热累积效应；后一层比前一层相同位置熔池尺寸有所增加，是由于已凝固层实体的导热率比粉末大很多以及一定的热累积作用。

(2)由于实体导热率比粉末导热率大很多，沿着扫描方向，熔池前端的温度梯度比熔池后端的温度梯度大。

(3)增加激光功率，熔池的温度、熔池三维尺寸都随之增加，然而，增加扫描速率，熔池的温度、宽度和高度都随之减小，熔池长度由于能量输入较高先增加后减小。激光功率太低或者扫描速率太高，会导致熔池深度太小，层与层之间不能很好的粘接；相反的，激光功率太高或者扫描速率太低，会导致熔池温度太高，造成材料的气化以及增大局部残余应力。