中考多解类问题

文/ 王嘉颖

在中考试题中，多解问题是一类常见而重要的问题.这类问题不一定最难，却容易失分.解决这类问题要多角度、全方位、深层次地思考，找到解题的突破口.

一、绝对值、参数方程、不等式中的多解

例 1 已知|a|=3，|b|=5，且ab＜0，那么a+b的值等于（ ）

A．8． B．-2. C．8或-8. D．2或-2.

解析：已知|a|=3，|b|=5，则a=±3，b=±5，

因ab＜0，即a，b的符号相反，

当a=3时，b=-5，a+b=3-5=-2；

当a=-3时，b=5，a+b=-3+5=2．

选D．

例2若关于x的分式方程无解，则实数m=_____．

解析：分式方程无解，则去分母后所得整式方程无解，或整式方程的解使分式方程的分母等于0，即增根．

方程去分母得7+3（x-1）=mx，

整理，得（m-3）x=4，

当整式方程无解时，m-3=0，即m=3；

当整式方程的解为分式方程的增根时，x=1，

∴m-3=4，即m=7，

∴m的值为3或7．

二、由函数的增减性产生的多解

例 3 如图1，在平面直角坐标系xOy中，函数y=kx+b（k≠0）与的图象相交于点A（2，3），B（-6，-1），则不等式kx+的解集为（ ）

图1

A.x＜-6. B.-6＜x＜0或x＞2.

C.x＞2. D.x＜-6或0＜x＜2.

例4 已知二次函数y=x2-2mx（m为常数），当-1≤x≤2时，函数值y的最小值为-2，则m的值是（ ）

解析：y=x2-2mx=（x-m）2-m2，

①若m＜-1，当x=-1时，y=1+2m=-2，解得

②若m＞2，当x=2时，y=4-4m=-2，解得（舍去）；

③若-1≤m≤2，当x=m时，y=-m2=-2，解得（舍去）.

∴m的值为或选D．

A.-2或3. B.-2或-3. C.1或-2或3. D.1或-2或-3.

解析：当m=1时，是一次函数，图象与x轴有且只有一个交点；

当m≠1时，它为二次函数，

解得m=-2或3.

∴m的值为1或-2或3.选C．

三、等腰三角形中，腰、顶角、高的不确定性产生多解

例6在等腰△ABC中，AD⊥BC交直线BC于点D，若，则△ABC的顶角的度数为______．

解析：①B为底，设AC=BC，

∵AD⊥BC于点

如图2，AD在△ABC内部时，顶角∠C=30°，

如图3，AD在△ABC外部时，顶角∠ACB=180°-30°=150°，

图2

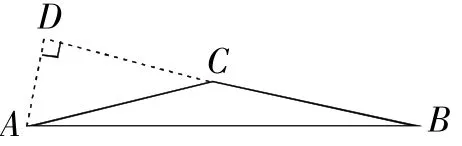
图3

图4

②BC为底，如图4，

∵AD⊥BC于点D，

∴∠B=∠BAD，∠C=∠CAD，

∴顶角∠BAC=90°，

综上所述，等腰△ABC的顶角为30°或150°或90°．

四、在直角三角形中，直角、斜边的不确定性产生多解

例7已知直角三角形有两条边的长分别是3cm，4cm，那么第三条边的长是（ ）

五、相似三角形中，对应边、对应角、对应位置的不确定性产生多解

例 8 在△ABC中，AB=6，AC=5，点D在边AB上，且AD=2，点E在边AC上，当AE=_____时，以A，D，E为顶点的三角形与△ABC相似．

解析：以A，D，E为顶点的三角形与△ABC有一个公共角∠A，因此，只需∠A的夹边对应成比例时，两个三角形相似.

∴AE的长为或

x+1与x轴，y轴分别交于A，B两点，

令x=0可得y=1，令y=0可得x=-3，

∴ 点A和点B的坐标分别为（-3，0），（0，1），

∵△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1∶2，

∴ 当点B′在第一象限时，B′的坐标为（3，2）；当点B′在第三象限时，B′的坐标为（-9，-2）．

∴B′的坐标为（-9，-2）或（3，2）．

图5

六、特殊四边形中，对边、邻边、高的不确定性产生多解

例10 在菱形ABCD中，AE为BC边上的高，若AB=5，AE=4，则线段CE的长为______．

解析：当点E在CB的延长线上时，如图6，

∵AB=5，AE=4，

∴BE=3，CE=BC+BE=8；

当点E在BC边上时，如图7，

∵AB=5，AE=4，

∴BE=3，CE=BC-BE=2．

∴CE的长是2或8．

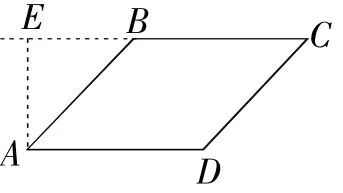
图6

图7

七、弦与弦、弧与弧、点与圆、直线与圆的位置关系的不确定性产生多解

例11 已知AB，CD是⊙O的两条平行弦，AB=6，CD=8，⊙O的半径为5，则弦AB与CD的距离为（ ）

A.1. B.7. C.4或3. D.7或1.

解析：①当AB和CD在O的同侧时，如图8，

过O作OE⊥AB于E，交CD于F，连接OA，OC，

图8

图9

∵AB∥CD，∴OF⊥CD，

在Rt△OAE中，

同理可得OF=3cm，EF=4cm-3cm=1cm；

②当AB和CD在O的两侧时，如图9，可得OE=4cm，OF=3cm，

则EF=4cm+3cm=7cm.

∴AB与CD的距离是1cm或7cm.选D．

八、图形位置关系不确定产生多解

图10

图11

图12

例 12 如图10，在△ABC中，AB=BC=8，AO=BO，点M是射线CO上的一个动点，∠AOC=60°，则当△ABM为直角三角形时，AM的长为_____．

解析：如图10，当∠AMB=90°时，

∵O是AB的中点，AB=8，∴OM=OB=4，

又∵∠AOC=∠BOM=60°，

∴△BOM是等边三角形，

∴BM=BO=4，

在Rt△ABM中

如图11，当∠AMB=90°时，

∵O是AB的中点，AB=8，∴OM=OA=4，

又∵∠AOC=60°，

∴△AOM是等边三角形，

∴AM=AO=4；

如图12，当∠ABM=90°时，

∵∠BOM=∠AOC=60°，∴∠BMO=30°，

∴MO=2BO=2×4=8，

在Rt△BOM中

在Rt△ABM中

综上所述，AM的长为或或4．