一道解析几何定值问题的探究与拓展

华南师范大学附属中学汕尾学校(516600)刘光明

无论是高考真题还是教研考试题都凝聚着智慧,都已深入挖掘某一知识领域,犹如数学花丛中一朵魅力之花,牵动着无数一线教师和教研工作者的心,备受青睐.最近有幸碰见一道解析几何定值问题,看似平淡无奇,精心思量其源远流长.经过可视化几何画板的探究和推理论证得到了一般性的结论,更甚者其逆命题也具有一般性结论,在此与读者共享.

1 .原题呈现与多解探究

试题如图1,已知椭圆C:的两个焦点分别为F1,F2,动点P在椭圆C上,△PF1F2的面积的最大值为√椭圆的右顶点与抛物线y2=8x的焦点重合.

(1)求椭圆C的标准方程;

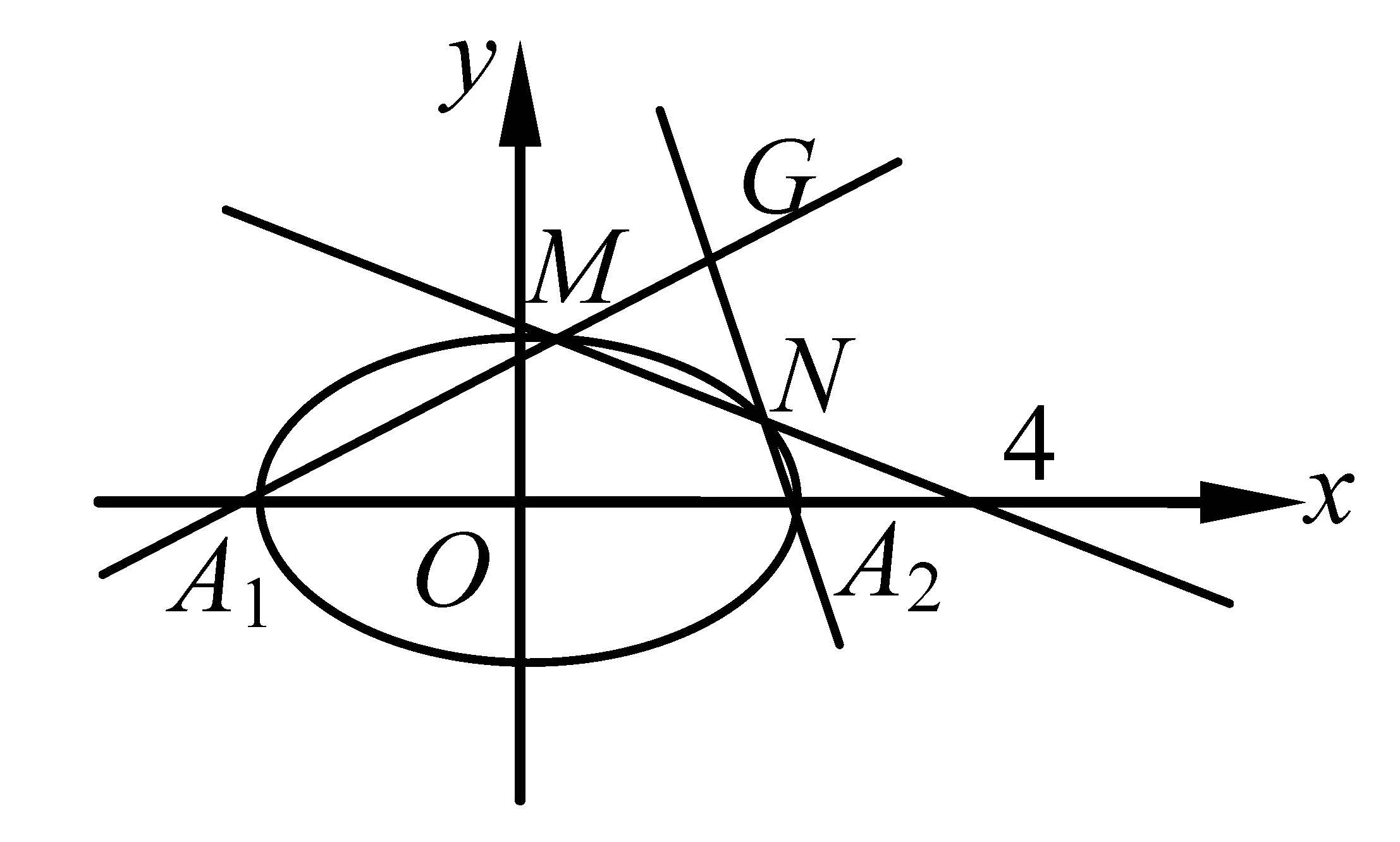
图1

(2)设直线l:y=k(x-4)(k/=0)与椭圆C交于M,N两点,记椭圆C的左、右顶点分别为A1,A2,设直线A1M,A2N的交点为G,求证：点G在定直线x=1上.

解析(1)抛物线y2=8x焦点坐标为(2,0),故椭圆右顶点为(2,0),即a=2,又又-b≤yP≤b,故△PF1F2的面积的最大值为cb=因为a＞b＞1,所以b=故椭圆C的标准方程为

(2)方法1设而不求,解出交点坐标.

由(1)可知A1(-2,0),A2(2,0),不妨设M(x1,y1),N(x2,y2),因为k/=0,所以M,N与椭圆顶点不重合,于是直线A1M方程为直线A2N方程为由

得

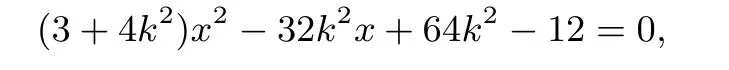
将(∗)式代入(∗∗)式化简整理可得：

因此点G在定直线x=1上.

方法2巧借三点共线,简化运算程序.

设M(x1,y1),N(x2,y2),G(x3,y3),由题意x1,x2,x3两两不等,因为B,M,N三点共线,所以所以又点M,N在椭圆上,于是

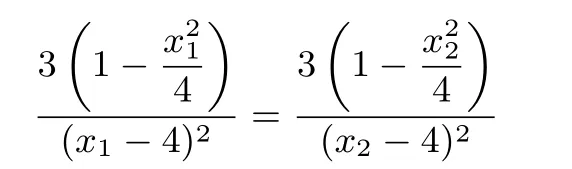
整理得：

又A1,M,G三点共线,故

另有A2,N,G三点共线,则

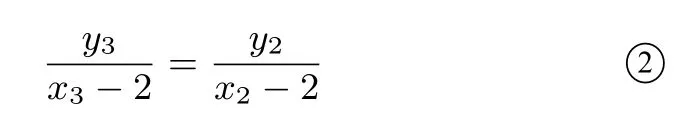
将①与②两式相除可得

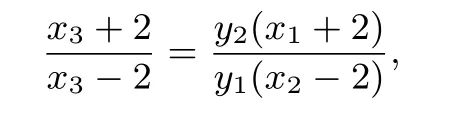
所以

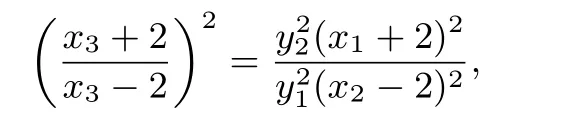
故

将2x1x2-5(x1+x2)+8=0即x1x2=-4代入可得,解得x3=4(舍去)或x3=1,所以点G在定直线x=1上.

点评直线与圆锥曲线相交问题,自然而然地联想到“设而不求”,通过联立方程消元后运用韦达定理处理,正如方法1所呈现出的基本历程,相比之下方法2巧妙借助一些几何关系(共线、垂直、平行、相似比等)可以简化一定的运算量,却不能很好求解交线的斜率范围,故而在解析几何的教学中需要关注几何直观素养的渗透.

2 .椭圆中一般性结论

性质1如图2,已知椭圆E:=1(a＞b＞0)的左、右顶点分别为A,B,过点的直线l与椭圆相交于两个不同点M,N,且M,N异于A,B两点,直线AM与直线BN相交于点G,则点G在定直线x=c上.

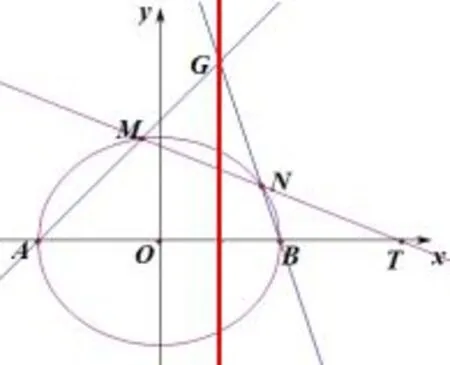
图2

利用几何画板的动态演示功能,先定参数a,b,让直线l的斜率改变,跟踪交点G的轨迹,则可观察到如图2所示垂直于x轴的直线,通过度量得到该直线方程就是x=c.有了这个直观感知,进一步推理证明如下：

证明由题意可知A(-a,0),B(a,0),直线l的斜率存在,不妨设为k,则直线l方程为

假设N(x1,y1),M(x2,y2),则直线AM方程为

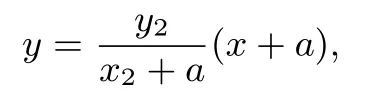
直线BN方程为

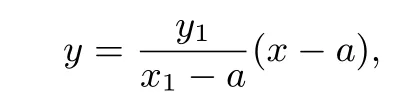
由

可解得

由

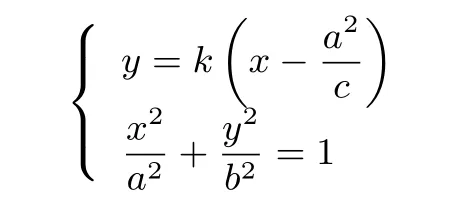
消去y可得

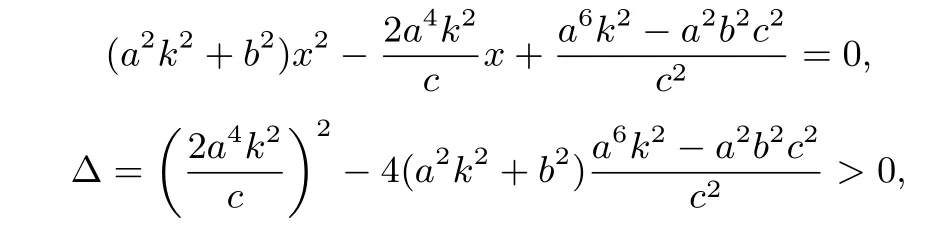
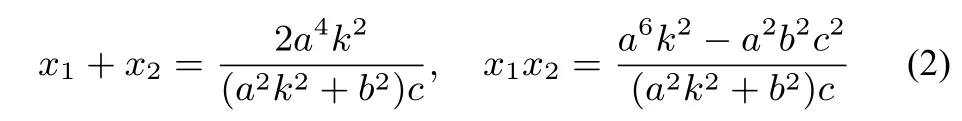
将(2)式代入(1)式化简整理可得

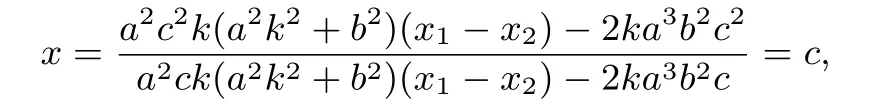
即点G的横坐标为xG=c,故点G在定直线x=c上,因此性质1成立.

点评若假定性质1中的参数取相应定值a2=4,b2=3,则直线过点T(4,0),点G在定直线x=c=1上,故原题是性质1的一种特殊情形.

3 .逆向探究

依照圆锥曲线的类比探究的思维惯例,借助几何画板的动态演示,经过理论的逻辑推导发现其逆命题也深藏玄机.=1(a＞b＞0)的左、右顶点分别为A,B,点G为直线x=c上的动点,且点G不在椭圆E上,若直线GA,GB与椭圆E分别相交于点M,N,则直线MN恒过定点

性质2如图3,已知椭圆E:

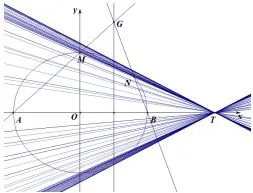
图3

证明假设点G(c,t),M(x1,y1),N(x2,y2),则直线GA方程为

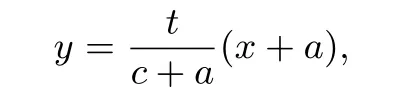
直线GB方程为

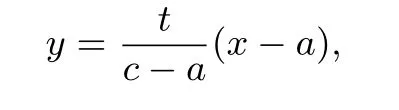
由

消去y可得

又xA=-a故

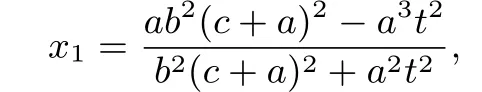
从而

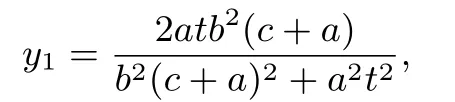
故点

同理可得点

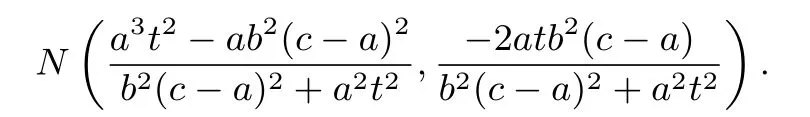
所以直线MN的斜率

因此直线MN的方程为

4 .运用类比思想,在双曲线中拓展

圆锥曲线的魅力就在于其丰富多彩甚至是无穷尽的性质,而思考探索的思路大都是采取类比推理进行推广拓展.通过超级几何画板进行探索(如图4所示),得到了双曲线中的一般结论,推理论证详见性质3.

性质3如图4,已知点A,B分别为双曲线E:1(a,b＞0)的左右顶点,过点的直线l与双曲线E相交于两个不同点M,N,且M,N异于A,B两点,直线AM与直线BN相交于点G,则点G在定直线x=c上.

图4

证明由题意可知A(-a,0),B(a,0),假设N(x1,y1),M(x2,y2),则直线AM方程为直线BN方程为

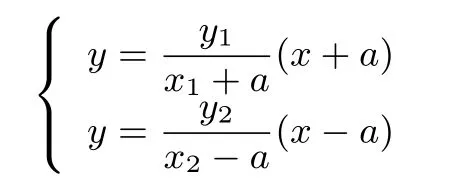
可解得

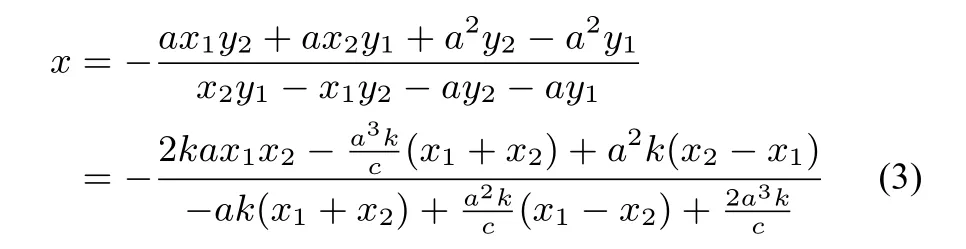
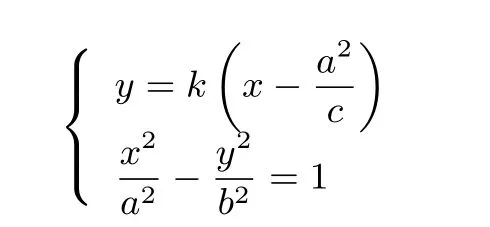
消去y可得

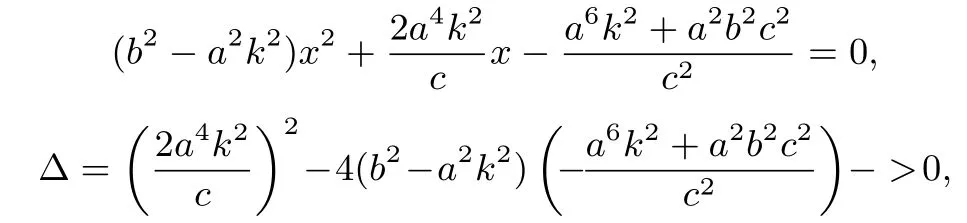
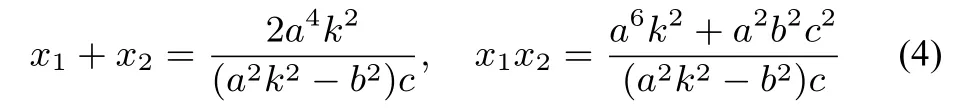
将(4)式代入(3)式化简整理可得

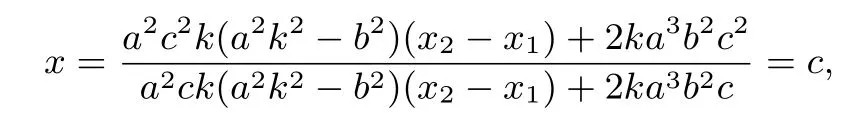
即点G的横坐标为xG=c,故点G在定直线x=c上.

性质4已知双曲线E:的左、右顶点分别为A,B,点G为直线x=c上的动点,且点G不在双曲线E上,若直线GA,GB与双曲线E分别相交于点M,N,则直线MN恒过定点

性质4的证明,有兴趣的读者可以模仿性质2证明过程进行,在此故不再赘述.

希尔伯特说“数学问题的宝藏是无穷无尽的,一个问题一旦解决,无数新的问题就会取而代之.”作为一个数学学习者而言,遨游在数学的海洋中,总会情不自禁地思考一个问题：解决前一问题的方法能否也能用来解决后续的一些延展性的问题,犹如波利亚所说“解数学题就像采蘑菇一样,当我们发现一个蘑菇时,在它的周围可能有一个蘑菇圈”.因此,数学教学的路途风景无限好,大胆假设,用心雕琢,细心求证才能品味出数学的迷人之处.