高速拖靶系统掠海飞行仿真研究
2018-08-11田新锋邓雨辰
田新锋,邓雨辰
(解放军92419部队,辽宁 兴城 125106)
拖靶系统作为一种特殊航空装备,随着防空武器试验和部队对空靶训练要求的不断提高,得到了迅速发展,品种不断增多,功能日趋完善[1-3]。特别是大速度超低空掠海飞行功能的扩展,可模拟低空掠海来袭导弹,进一步提高靶标的真实度。当系统速度提升,低空掠海飞行时如果策略选择不当,在外部环境干扰下,可能导致系统无法实现掠海飞行,也可能导致拖靶入水坠毁。因此需对拖靶超低空掠海定高飞行的使用边界进行研究,提高系统使用安全性。本文针对某拖靶系统速度提升后如何进行掠海安全飞行这一现实需求,分析了拖靶定高飞行工作原理,建立了系统仿真模型,给出了拖靶超低空掠海定高飞行的使用边界,为某新型拖靶大速度超低空掠海飞行提供理论依据。
1 拖靶工作模式
拖靶不同于一般飞行器,其本身无动力,靠拖带飞机(简称拖机)拖曳飞行。典型的现代航空拖靶系统由拖机、航空绞车、拖缆和拖靶等部分组成[4]。
其典型任务工作剖面如图1所示,拖机挂装航空绞车拖靶起飞后,首先爬升至放靶高度,保持高度速度匀速释放拖缆放出拖靶,拖缆长度释放至预定长度(一般为5000 m),停止释放拖缆,然后降高至预定基准高度,调整速度航向进入航路,控制拖靶高度控制系统工作,拖靶模拟来袭导弹做掠海恒高飞行。舰艇上的火炮、导弹等武器系统则可以对目标进行捕获、跟踪、射击或模拟射击,如果需要可进行第二次供靶进入,任务结束后拖靶高度控制系统停止工作,拖机爬升到收靶高度以上,并调整速度进行收缆收靶,直至最后拖靶在绞车上复位后,拖机返航。
2 拖靶定高飞行工作原理
由系统工作剖面可确定拖靶定高飞行时的高度关系,如图2所示所示。从图中可以看出,拖靶定高飞行高度h与拖机基准飞行高度f(m)、拖缆下沉量f(n)有关。即拖靶的飞行高度h由下式确定:
h=f(m)-f(n)
(1)
式中,f(m)为任务前设计的定值,飞行过程中,拖缆对拖机的牵引力是变化的,牵引力变化可看做是作用于拖机上的干扰力,而拖机靠调节发动机推力和控制参数,仍可实现稳定飞行,保证f(m)的偏差在设计误差范围内,可认为f(m)在飞行过程中不变。
式中f(n)为一变化量,当一定长度的拖缆在拖曳飞行时,两端分别受到拖机的牵引力、拖靶的拉力作用,同时受气动力、自身重力作用,在这些外界力共同作用下,拖缆的下沉量就不同,拖靶的飞行高度也不同。
拖靶要实现定高飞行,就是通过对拖缆拉力进行调整,使拖缆下沉量维持不变。其中拖靶对拖缆的拉力主要由于拖靶重力、飞行气动力和高度控制系统作用时的附加气动力组成。当拖靶实际飞行高度与预定高度存在高度差时,高度控制系统控制舵面会产生一个附加的气动力,由于拖缆两端受力发生,其下沉量也随之变化,从而实现系统的定高飞行。当高度控制系统产生的附加气动力引起的拖缆下沉量变化不足以消除高度误差时,则不能实现定高飞行。
通过上面分析可以看出拖靶要实现定高飞行,首先拖机基准飞行高度f(m)要合理有效,其次拖靶的舵面效率足够高,能够克服外界干扰带来的拖缆下沉量f(n)变化。
3 系统建模
由式(1)可知,要设计f(m)必须知道f(n)和h,对于某一特定任务,h已知那么只需确定任务状态下的f(n)即可。那么需建立拖靶和拖缆动力学模型[5-6]。
拖靶系统的工作情况是比较复杂的,一方面拖靶连同拖机做各种随动飞行,另一方面又相对于拖机做相对运动。但是在实际拖靶定高飞行时对拖机飞行情况加以限制,要求拖机做平直匀速飞行,不考虑横侧向运动,使系统建模得以简化。
3.1 拖靶受力模型分析
拖靶挂机状态下,受拖缆的拉力T、升力L、阻力D、力矩M,拖靶自身重力mg,受力分析如图3所示。
则在速度坐标系下,拖靶纵向动力学方程如下:
(2)
式中,θ为拖靶姿态角,γ为航迹角,α为迎角,φ为拉力与机体轴夹角。
有了拖靶的受力模型,就可以确定在不同速度下,拖靶不同舵翼角工作状态下对拖缆的拉力大小和方向,为拖缆下沉量的计算提供条件。
3.2 拖缆受力模型分析
对于拖缆这样的柔性细长体,长度达5000 m,直径只有几毫米,研究其运动时,既不能将其看成一个质点,也不能将其看成一个刚体。这里,采用微积分中的研究方法,将拖缆分割成无数个拖缆微元,把每个微元作为一个质点来研究其受力与运动,这样就能得到微分形式的拖缆飞行动力学模型。
不妨设拖缆与拖靶连接处为零点,在拖缆长度为s处取一长度为Δs的拖缆微元,则该拖缆微元两端受到的拖缆张力分别为T和T+ΔT,拖缆水平运动速度为u,垂直速度为v,拖缆气动阻力为D,升力为L,微元质量m,那么拖缆微元受力分析如图4所示。
那么有
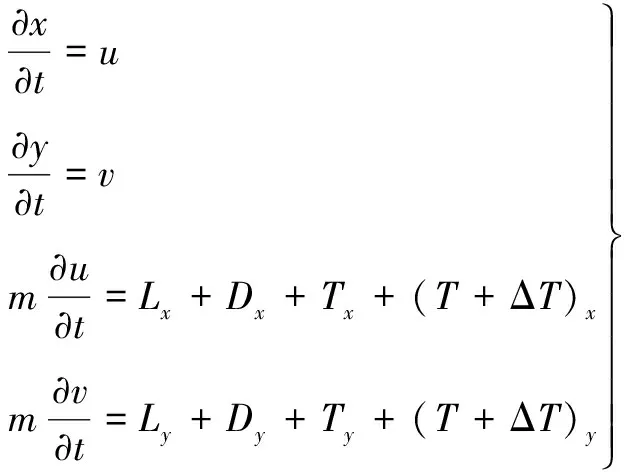
(3)
有了拖缆微元的受力模型,就可以确定该微元在空间的状态,通过迭代法就可求出整个拖缆的状态空间分布,进而确定拖缆两端的张力情况和总的拖缆下沉量。
4 仿真结果分析
4.1 仿真初始条件
假定系统工作在理想环境条件下,其初始数据如下:
拖靶质量m=40 kg;
拖靶参考面积S=0.03 m2;
拖靶参考长度L=3.5 m;
拖靶舵面工作范围δe=-6°~2°;
拖缆长度l=5 000 m。
4.2 仿真结果分析
基于拖靶初始数据和系统模型,可确定拖靶舵翼角在不同速度下与拉力关系曲线,如图5所示,进而可确定不同速度、舵翼角下的拖缆的下沉量,如图6所示。
从图5、6中可以看出,随着舵翼角的偏向负值,会产生一个向下的力,加载在拖缆端的拉力随之增加;由于拖缆两端的张力增加,拖缆的下沉量也增加。随着速度增加,拖靶气动力增加,拖靶对拖缆的拉力增加,但拖缆的气动力也增加,综合结果拖缆下沉量减小。
因此在拖靶定高飞行速度增加后,拖机的基准飞行高度要降低,掠海飞行速度由Ma=0.45提高到Ma=0.6,拖机的基准飞行高度要降低120 m左右。实际飞行掠海低空飞行过程中,拖机的高度有原先的450 m调整为330 m,最低不能低于320 m,否则可能导致拖靶水,最高不能高于370 m,否则拖靶无法达到掠海定高飞行的目的。依据该方法,指导了后续研制飞行试验,取得了满意的效果,结果表明该方法合理有效。
5 结束语
拖靶系统提高飞行速度,在模拟低空掠海来袭导弹方面,提高了靶标的真实性和有效性。而系统速度提升后,如何确立系统的使用边界,选择拖曳基准飞行高度就显得尤为重要。本文针对拖靶系统速度提升后,如何确立拖机新的使用边界进行了研究,完成了以下工作:
1)通过对拖靶定高飞行工作原理进行分析,确立了问题分析的对象;
2)通过对拖靶、拖缆进行建模分析,确立了两个模型见相互作用的耦合点;
3)结合实际条件,对系统进行了仿真计算分析,结果表明,系统速度提升后,要实现超低空掠海安全飞行,拖机的基准飞行高度要降低120 m,并在系统科研试飞试验中得到了验证,取得了满意效果,为系统速度提升后的使用提供理论依据,对系统的推广使用而言具有重要的现实意义。
