测向交叉定位体制下平台航迹最优规划算法
2018-08-11张志虎赵佳旻
张志虎,赵佳旻,刘 梅
(1.中国电子科技集团公司第二十九研究所,四川 成都 610000;2.哈尔滨工业大学电子与信息工程学院,黑龙江 哈尔滨 150000)
单站被动雷达的可观测性较弱,其航迹优化的过程是提高跟踪系统可观测性的过程,从而能够达到提高定位以及跟踪精度的主要目的。然而在实际应用中,有的时候飞行平台并不能毫无限制地按照最优的轨迹进行运动。当空间内存在敌方目标,如防空火炮、敌方雷达等限制区域时,飞行平台的飞行轨迹便受到了种种限制,所以只研究无限制条件下的轨迹优化是没有太多的使用价值。此时就要针对存在限制条件下的飞行平台轨迹优化进行一定的研究。本文的研究重点在于引用了最小化克劳美劳下界(CRLB)的迹(GDOP)[1]作为性能指标来研究观测平台的最优轨迹,从而使雷达系统的跟踪误差最小。
1 无限制条件下的轨迹优化
1.1 问题描述
对于单站被动雷达,若要对空间上的飞行目标进行定位,需要观测平台的运动阶数高于目标运动阶数,此时,观测平台如何运动才能使目标的跟踪误差最小,成为我们研究的主要问题。本文假设环境理想,即观测平台可以在三维空间内无限制条件地自由运动,目标和观测平台在空间的位置关系如图1所示。
其中,βj为j时刻目标相对于观测平台的真实方位角(以正北为参考方向)。
1.2 定位与跟踪误差的下限
对于无限制条件下轨迹优化的研究,通过引入目标定位跟踪精度下限CRLB(Crammer-Rao Lower Bound,CRLB),以及通过CRLB计算出的精度几何散布GDOP(Geometric Dilution of Precision,GDOP)作为航路优化的指标,采用单步寻优的方式,避开了在复杂的全局寻优方法中要求目标固定或目标的运动速度和航向必须已知的困难。
CRLB[2]是研究平台对目标的某一航迹的跟踪效果的评价指标,下面给出定义。
定义P为对应任何位置确定变量无偏估计器的估计误差协方差矩阵。下列不等式成立:
(1)
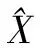
在上述模型和噪声的条件下,到k时刻为止,理想的估计误差下限CRLB为
(2)
式中:Hj=[cosβj-sinβjjT·cosβj-jT·sinβj],T为观测平台的采样间隔,Rj为观测序列β的协方差矩阵。
所以到k时刻为止,根据式(2)可以得到i时刻状态XT(i)的CRLBXT(i)理想估计误差下限为
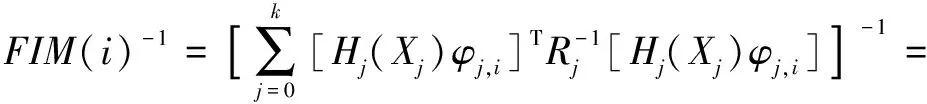
(3)
其中,φj,i为目标状态转移矩阵。
目标初始状态XT(0)=[rx0,ry0,vx0,vy0],其中,rx0,ry0为目标初始时刻的位置信息,vx0,vy0为目标初始时刻的速度信息。XT(0)的理想估计误差下限为
CRLBXT(0)=FIM(0)-1
(4)
(5)
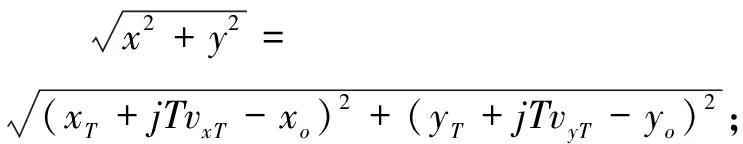
其中,rj为目标与观测平台的径向距离;xT,yT为目标的位置;xO,yO为观测平台位置;vxT,vyT为目标运动速度。
上述选状态变量为:X=XT(0),即目标初始状态。而EKF形式计算CRLB时,状态变量为每一个时刻的目标状态X(k)。所以,采用EKF的形式计算第i时刻的CRLB为
(6)
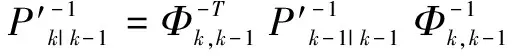
(7)
初始条件为
所以
(8)
从CRLB或FIM的元素表达式可以知道,每一个元素同观测平台的位置坐标相关,因此雷达系统观测平台运动轨迹的优劣就能通过这个指标反映出来。
本文取几何定位散布精度GDOP(Geometric Dilution of Precision,GDOP)评估的目标函数,即性能指标,GDOP就是理想估计误差下限CRLB的迹函数。其定义为
(9)
GDOP同CRLB有关,CRLB的表达式非常复杂,这里采用数值计算的方法来计算单观测器测向无源定位的误差下限CRLB,以找出影响定位精度的主要因素,说明观测器运动轨迹对定位精度的影响。
1.3 最优航路算法
不难看出:在计算每一时刻的GDOP值时,利用了全部跟踪时长的信息,然而往往在实际应用中,这种算法显然是无法实现的,因为跟踪时只可能利用到跟踪时刻之前的信息,其之后的信息并无法获得,所以在进行航路优化的时候需要使用EKF滤波算法,即进行单步优化[3],如式:
(10)
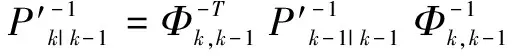
(11)
初始条件为
(12)
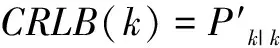
(13)
GDOP计算表达式为:
(14)
GDOP的值反映了速度和位置估计误差大小。在某一运动方向下,使得GDOP值最小,说明观测器朝该方向运动能获得较高的定位跟踪精度。该准则下最优轨迹求解的过程比较复杂,在单步轨迹优化的过程中,本文使用的方法为等间隔搜索法。如图2所示。
一般情况下,平台离目标越近,定位精度越高。故平台最优轨迹搜索范围可定为目标与平台方向的左右90°将该范围分为N-1等份,然后逐一进行搜索比较,寻找使得GDOP值最小的观测器运动方向。具体算法流程见图3所示。
2 只采取180°转弯条件下的最优航迹规划问题
2.1 方位角变化率最大算法(跟踪时长已知)
对于平台只采取180°转弯的情况,本文采用的方法是全局方位角变化率最大算法。
本文取以观测器为原点的载机直角坐标系,如图4所示。为了研究方便,假定辐射源与观测站处于同一个平面内,这就形成了二维定位问题。通常将这种定位方法称为三角定位法(即BO定位方法)。在二维条件下观测站O以速度V=(vox,voy)T运动时,它与地面固定目标M=(xi,yi)的连线ri斜距其大小为距离:
(15)
(16)
(17)
(18)
(19)
(20)
此时目标辐射源的到达观测平台的方位角为βi。
由图4可知:
(21)
当不存在噪声和干扰,即不存在测量误差时,对于同一辐射源,方位线精确地相交于一点,该点就是辐射源的位置。但测量误差或干扰总是存在的,同一辐射源2条以上的方位线一般来说不可能确定唯一的交点。因此为了确定辐射源的位置,就必须使得单位时间的方位角变化速率尽可能地大,以减小测量误差对目标定位的影响。
方位角变化率最大准则下的观测器轨迹,可以改善对目标的定位跟踪性能。在噪声方差一定的情况下,当观测器机动使得方位角变化率最大时[4],测量数据的信噪比最大,从而提高对目标的定位精度。
在无限制条件运动时,观测器机动的思想为[5]:
1)保持有最大接近率,并使β保持常数的航向;
2)当有测量噪声时,使dβ/dt进行最大的机动。
但在实际应用中,存在着种种限制条件,本文研究的特殊情况是飞行器初始飞行方向以及跟踪时长已经确定,并且只能进行一次转弯从而折返的情况下,无法完全满足上述机动思想。如过转弯时间过早,则会造成飞行器跟踪末期距离目标过远,跟踪误差会增大。如果拐弯时间过晚,则跟踪无法收敛。所以为了寻找一个合适的拐点,只能对上述机动思路进行最大程度地接近从而取得次优的跟踪线路[6-8]。
于是退而求其次,本文采用使所有跟踪时间内,每时刻的方位角变化率总和最大的思路求出飞行器运动过程中返航的拐点。
本文所探讨的限制条件可简单描述如下:
如图5所示,平台在已知的跟踪时间内,只能在目标单侧进行直线运动,并且需要选择在某个时间点拐弯进行返航。其每一时刻的方位角变化率为Δβi,径向距离为ri,单位时间内前进距离为Δx。
易知每一时刻的方位角变化率为
Δβi=Δx/ri=v·Δt/ri
(22)
现要求出使得总的方位角变化率
(23)
最小的飞行器拐点。从图5中可看出,当飞行器接近目标与飞行轨迹垂线焦点A的时候,其径向距离ri总是在减小,故方位角变化率一直在增大,所以无论飞行器初始条件如何,其从初始位置一直到A点运动的这段距离总是使方位角变化率增大的。所以如何计算拐点在飞行器到达A点之后计算余下的路程即可。
现证明:在飞行器到达A点之后,在剩余跟踪路程的1/3处拐弯返航即可使得方位角变化率最大。
如图6,在飞行器到达A点后在剩余跟踪路程1/3折返的基础上,如果延迟Δx的路程折返,如图ab段,则会多出两段ab而减少一段cd。很容易看出来,ab段的径向距离r远远大于cd段的径向距离r,所以ab两段积累的Δβ要小于cd一段积累的Δβ,故之前拐点的方位角变化速率全局最大。
同理,如果提前Δx的距离拐弯,则方位角变化速率同样会减小,所以最佳拐点为飞行器到达A点之后剩余跟踪时长的1/3处。
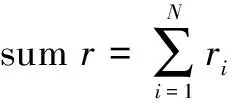
2.2 航迹优化算法(跟踪时长未知)
当飞行平台的跟踪时长未知的话,就无法采用全局方位角变化率最大算法。此时所采取的方法是通过实时对跟踪误差变化趋势的监视来选择180°转弯的时机。
已知系统的跟踪误差为
(24)
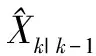
随着跟踪进行,V(k)是时刻变化的,当跟踪开始一段时间后如果V(k)是持续发散的则需要平台采取180°转弯机动,使跟踪误差收敛。平台转弯结束后继续监视跟踪误差V(k),如果其又有发散的趋势或者收敛程度未达到要求,则继续进行180°转弯,直至跟踪时长结束。
3 仿真测试
3.1 无限制条件下的轨迹优化
场景设置:跟踪时长3000 s,雷达侧角误差标准差0.1°(5 mrad),仿真考虑雷达观测目标运动的情况。目标初始位置(0 km,0 km),目标速度15 m/s,平台初始位置为(-50 km,-10 km),平台速度为(0,150 m/s)。雷达方位角误差的标准差σ均为0.1°(5 mrad)。雷达方位角的观测范围为-180°~180°,在该观测范围内杂波均匀分布且每帧杂波数目λ=5。雷达漏检概率为0.02。实验中雷达采样周期为1 s,取8个采样周期的数据进行航迹起始,其中第1个和第8个采样周期的测量数据用来形成候选目标集。实验结果如图7、8所示。其中,图7为生成的场景。
雷达相对目标的飞行航迹能影响其跟踪效果,通过图7可以发现,通过本文所说的方法所产生的优化航迹是逐渐接近目标的螺旋形,符合理论研究所得的结论。而从跟踪结果上来看,跟踪开始的误差为2500 m左右,在平台进行了一定时间的机动后跟踪误差快速收敛,并维持稳定于10 m量级,说明航迹优化算法的有效性。
3.2 只采取180°转弯条件下的最优航迹规划问题(时长已知)
实验场景设置:跟踪时长3000 s,雷达侧角误差标准差0.1°(5 mrad),平台速度150 m/s正北方向,初始位置(-10 km,-10 km),目标固定,初始位置(0,0),于最佳拐点处拐弯(1000 s)。如图9所示。
场景跟踪结果,如图10所示。
平台选择在方位角变化率全局最优的拐点处拐弯,从图11中可以很明确地发现,跟踪误差在拐点处迅速收敛,并稳定维持于几十米左右,跟踪效果较好。
3.3 只采取180°转弯条件下的最优航迹规划问题(时长未知)
实验场景设置:跟踪时长3000 s,雷达侧角误差标准差0.1°(5 mrad),跟踪系统监视跟踪误差,当其在100 s内跟踪误差持续增长时平台就采取180°转弯机动。平台速度150 m/s正北方向,初始位置(-50 km,-100 km),目标速度5 m/s正北,初始位置(0,0)。
实验结果:
从跟踪误差上可以看出,当误差在700 s左右有上升趋势的时候,平台进行了180°的转弯机动,随后跟踪误差迅速下降并收敛到很小的量级。说明理论的正确性。同时,如果继续跟踪的话平台继续远离目标,跟踪误差可能继续增加,这时只要采取相同的对策直至跟踪时长结束即可。
4 结束语
本文对测向交叉定位体制下平台航迹最优规划算法分别进行了研究并给出了详细的解决方案,提出的三种不同的航迹优化算法能够对所对应的三种跟踪场景进行有效的优化,从仿真结果的误差示意图上能够明显看出优化前后误差的变化。通过方案论述以及各种条件下的仿真验证,表明了本文所提方案的合理性以及适用性,可以应用于工程实践中。
