培养中年级学生思维敏捷性

梁 寒

（南京民办实验学校，江苏 南京）

数学是思维的“体操”，可以锻炼学生的思维能力，使其不断地发展。学生处在中年级向高年级过渡时期，思维能力的发展处在转折时期，抽象概括、分类、比较和推理能力开始慢慢形成。题目量在增加，题目难度也在提高，这也决定了对学生思维敏捷性的要求也在提高。如何才能提高学生的思维敏捷性呢？

一、提高数学运算能力

针对中年级教材内容主要提高学生两位数乘两位数、三位数乘两位数的笔算能力、除数是两位数的除法计算以及运用运算律进行简便运算的能力。首先学生应该在理解算理和算法基础上进行正确计算，结合实际问题感受简便运算。

①月星小区有16幢楼，平均每幢楼住128户。月星小区一共住了多少户？

例如上图：在教学三位数乘两位数笔算时，结合学生已有的认知，学生会说可以先计算6栋楼共住了多少户，然后再算出10栋楼共住了多少户，最后加起来。经历这个过程学生就会理解竖式计算的算理，更能深入地理解每一步求出的是什么，真正学透，而不是机械式地计算。这样举一反三的能力也会慢慢提高。

再例如学习乘法结合律时：如下图，

④华丰小学举行跳绳比赛，规定每个班选派23人参加。每个年级有5个班，6个年级一共要选派多少人参加比赛？

再写几组这样的算式，算一算，比一比，你有什么发现？

如果用字母a、b、c分别表示三个乘数，上面的规律可以写成：

先出示例题，让学生理解题意，出示问题：要求6个年级一共要选派多少人参加比赛？你是怎么想的，根据以前学过的连乘，学生会想到可以先求出6个年级一共有5×6=30（个）班，然后再根据每班23人就可以求出一共多少人参加比赛，列成综合算式就是23×（5×6）；同样也会有学生想到可以先求一个年级有多少人参加，列式是23×5，再乘6就可以求出6个年级一共要选派的人数，列成综合算式是（23×5）×6，如果顺序不同教师可以引导学生稍微调整，因为这样比较可以看得更清晰。学生通过思考过程会知道两种算法结果肯定相等，进而会得出乘法结合律。经历这一系列过程学生就更能理解什么是乘法结合律，这样在纯计算时学生就不是冷冰冰地计算，脑子会想到这一场景，错误率就会减少。

还有教学乘法分配律时：如下图

四、五年级一共有领多少根跳绳？

乘法分配律是个难点，学生掌握得一直不太好，这就要反思在教学例题时有没有让大部分学生理解这两种方法之间的联系。第一种方法学生可以先算出四五年级一共有10个班，再根据每班领24根跳绳，可以求出一共要领多少根跳绳。第二种方法是把四年级和五年级的跳绳分别求出来，然后把两个年级跳绳加起来。最后根据两种方法算出相等得出乘法分配律，这一步应该让学生多说，点名说，同桌互说。理解清楚两个数的和乘一个数应该等于这两个数分别乘一个数再相加。

所以学生的计算能力的培养离不开情境教学，计算能力增强了，学生思维敏捷性也会得到提高。

二、增强空间想象能力

空间想象能力就是学生对客观事物的空间形式进行观察、分析和抽象思维的能力。这种数学能力的特点在于善于在头脑中构成研究对象的空间形状和简明的结构，并能将对实物所进行的一些操作在头脑中进行相应的思考。例如：

③你会把方格纸上的三角形绕点A逆时针旋转90°吗？

例3是教学旋转知识，出示图片后先让学生动手旋转试试，看看用实物旋转后三角形位置，让学生通过实际操作先在脑中建立表象，然后慢慢表象加深后学生就要通过空间想象旋转后的图形位置，最后动手画出来。

三、提高解决问题的能力

“问题是数学的心脏”，通过解决问题培养学生自主性、创造性和解决问题的能力，学生平时会出现以下情况：有时，面对数学问题，无从下手；有时，明明思路很清楚，就是解不出来；有时解题到途中，却是“山穷水尽”。所以在教学中老师要求学生通过认真审题—画图—分析数量关系—列式解答—检验等步骤来完成。还会通过一些对比练习进行区分理解。

例如在教学相遇问题时，如下图：

小明和小红同时从马路的同一地点出发，同向而行。小明的速度是70米/分，小红的速度是60米/分，出发4分钟后两人相距多少米？

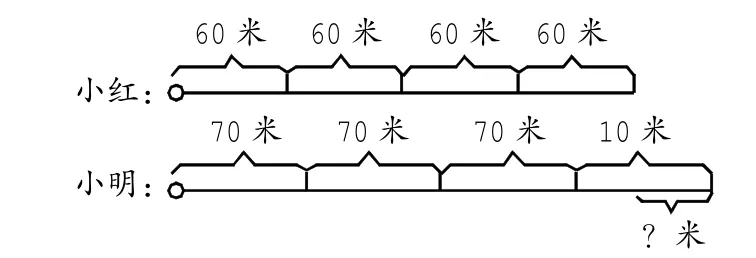
小明和小红同时从马路的同一地点出发，相背而行。小明的速度是70米/分，小红的速度是60米/分，出发4分钟后两人相距多少米？

这两种题型就是和学生做一个对比讲解，同一个地点、同时同向行驶时求两人相距路程是求两人路程之差。同一地点、同时相背而行时求两人相距路程是求两人路程之和。这两种题型不管是画图还是思路上都是有所不同的。

四、加强动手操作能力

动手操作是学生根据教师教学情景的创设，通过动手操作学具来探究数学问题，获得数学结论，并因此更好地理解数学知识的教学手段。数学是一门抽象的学科，组织学生进行操作活动，促使学生手、脑、眼、口多种感官参与学习，提高感知效果，为学生认识抽象的数学概念打下良好的基础。四年级下册第七单元学习了认识三角形、平行四边形和梯形，在学习中教师注重让学生通过动手拼一拼、量一量、测一测等活动，让学生发现知识。

例如在教学三角形内角和是180°时，如下图：

想办法把每个三角形的3个内角拼在一起，看看拼成了什么角。

自己再任意画一个三角形，先剪下来，再拼一拼。

让学生先动手操作，可以量一量三个角的度数再加起来；可以把三个角撕下来拼一拼；也可以把三个角折在一起。通过学生自己的探索会发现三角形内角和是180°。

基本技能的训练是数学知识转化为数学能力与素养的中心环节，它不仅在知识过程中对领会与巩固知识起促进作用，而且在知识深化形成高层次新知识中起桥梁作用，使学生实践能力、思维能力、创造能力得到培养，综合素质得到提高！

强化技能训练一定要在学生切实理解运算法则、定律、性质等基础上，要求学生熟记一些常用的数据，平时坚持适量的口算和应用题练习，通过视算、听算、口答、速算比赛等，采用“定时间比做题数量”“定做题数量比完成时间”的训练方式，强化学生的基本技能，从而达到培养思维敏捷性的目的。