基于邻域搜索的穴盘苗移钵路径优化蛙跳算法

徐守江，罗竹青

(江苏食品药品职业技术学院 a.信息工程学院;b.校企合作办公室，江苏 淮安 223003)

0 引言

在穴盘苗培育过程中，常出现穴盘内育苗不成功的情况，主要是由于漏栽和钵苗发育不正常引起，成苗率在90%左右[1]。机械化批量移栽近年来被广泛应用于补苗环节，农业钵苗移栽机器人通过视觉检测出不健康钵苗，将不健康钵苗剔除后通过机械臂带动末端执行器完成补种作业[2]。补种作业是将移栽穴盘中的部分健康钵苗逐一依次补种到目的穴盘中，移钵距离的长短由补种顺序直接决定；而目的穴盘中待补种穴盘位置与移栽穴盘可移栽钵苗位置均存在不确定性与多选择性，可选择的移钵路径随待补种穴盘数和可移栽钵苗数呈指数级增长。两穴盘中的孔穴位置距离固定，移栽路径越短，工作效率越高。遍历算法的排列组合式解法由于计算机的运行速度和存储容量限制无法在实际应用中得到推广。目前，工程上采用的移钵方法主要是固定顺序法，该方法按照固定顺序的方式进行移栽，移钵路径未经过优化。自动移钵问题类似于旅行商问题，但移钵问题需要交叉选择移栽穴盘与目点穴盘的孔穴且移栽穴盘无需遍历。近年来，诸多学者将遗传算法、蚁群算法和贪心算法成功应用于移钵路径的优化[3-5]，有效缩短移钵路径，提高了移钵效率。文献[3-4]中的算法均存在搜索空间大以及收敛速度慢等问题，增加了搜索时间。文献[5]的贪心算法实时性能好，能在有效时间内规划出优化路径，但优化的路径仍有待于进一步提升。

2003年，Muzaffar Eusuff 和Kevin Lansey提出了混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)，并成功应用于水资源网络优化问题[6]。蛙跳算法作为一种新的仿生算法逐步应用于机器人路径规划[7-8]、旅行商问题[9-10]及函数优化[11]等，主要用于解决组合优化问题，具有算法简单、调整参数少及寻优能力强等优点。本文基于混合蛙跳算法，针对穴盘苗自动移钵问题提出了局部分块搜索策略，融入交换因子、交换序和交叉操作等思想。同时，由于自动移钵问题的特殊性，在选择移栽穴盘时引入邻域搜索策略，有效限制搜索空间，较好地解决了本文路径规划问题。仿真实验表明，本文算法能有效规划出较优化移钵路径。

1 混合蛙跳算法基本模型

混合蛙跳算法是模拟青蛙觅食过程的一种基于群体的智能协同仿生算法。青蛙群体在寻找食物过程中通过局部搜索和全局信息交换来进行信息传递。在信息交流初期将初始青蛙种群划分为若干个族群，在每个族群内部执行局部搜索策略，实现族群内青蛙个体之间文化的交流。局部搜索每执行一段时间后，混合所有青蛙个体实现全局信息交换，并对青蛙群体重新划分族群再次进行局部搜索。重复上述过程，直至收敛的条件满足为止。

1.1 基本概念

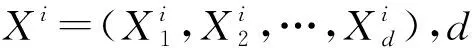
1.2 局部搜索

局部搜索的目的是使得各族群内个体在不同的方向上搜索局部最优，同时使得局部最优个体逐步向全局最优个体搜索。将青蛙群体划分为m个族群后，为了避免局部搜索过早陷入局部最优，在每个族群内按照一定的选择方法选取若干青蛙个体组成子族群进行局部搜索。假设全局最优青蛙个体为Xg，子族群内的最优青蛙个体为Xb,最差个体为Xw。子族群内的最差个体Xw更新策略为

D=rand( )×(Xb-Xw),rand( )∈(0,1),
D∈[Dmin,Dmax]

(1)

Xnew=Xw+D

(2)

新产生的青蛙个体Xnew，其适应度值若优于Xw，则用Xnew替换Xw；否则利用Xg代替Xb重复执行式(1)、式(2)一次，若新产生的青蛙个体Xnew仍不优于Xw，则随机产生一个新青蛙个体替换Xw。

1.3 全局信息交换

当所有子族群经过一定次数的局部搜索后，混合所有青蛙个体按照适应度值重新排序，根据族群划分规则重新生成族群，再次执行局部搜索操作，重复上述的局部搜索与全局信息交换直至满足收敛条件。全局信息交换便于各个族群内的信息交流，青蛙个体间的信息得到充分传递，便于青蛙个体寻找新的全局最优解搜索方向。

2 基于邻域搜索策略的移钵路径优化蛙跳算法

2.1 移钵路径规划问题描述

工程上农业钵苗自动化移钵样机由4部分组成，分别为识别系统、控制系统、输送系统和移钵系统，通过4个子系统间的协作有效完成目的穴盘不健康钵苗识别与剔除及移栽穴盘中健康穴苗的移钵与补种作业。图1为移栽穴盘和目的穴盘外围尺寸均为250mm×500mm、规格大小均为50的移钵工作示意图。图1中：白色小圆圈表示空的穴孔，即在目的穴盘中表示待移栽穴孔，移栽穴盘中表示当前穴孔不存在可移栽钵苗；灰色和黑色小圆圈均表示目的穴盘或移栽穴盘中的当前穴孔存在健康钵苗。

建立直角坐标系XOY，移栽钵苗主要是指机械臂带动末端执行器从原点O出发，逐一选取移栽穴盘中的健康钵苗并补种到目的穴盘中的待补种穴孔，如此反复不断执行补种作业直至目的穴盘中无空穴存在，最终返回原点O，图1中的路径即为一次移栽路径。为了便于表示移栽路径信息，将目的穴盘中的M个待补种穴孔依次编号为(-1，-2，-3，…，-M)，移栽穴盘中的含可移栽健康钵苗的N个穴孔编码依次为(1，2，3,…，N)，编号顺序均为从上往下、从左到右。图1中，移钵路径序列则可线性表示为{0，11，-4，3，-3，4，-2，9，-1，0}。

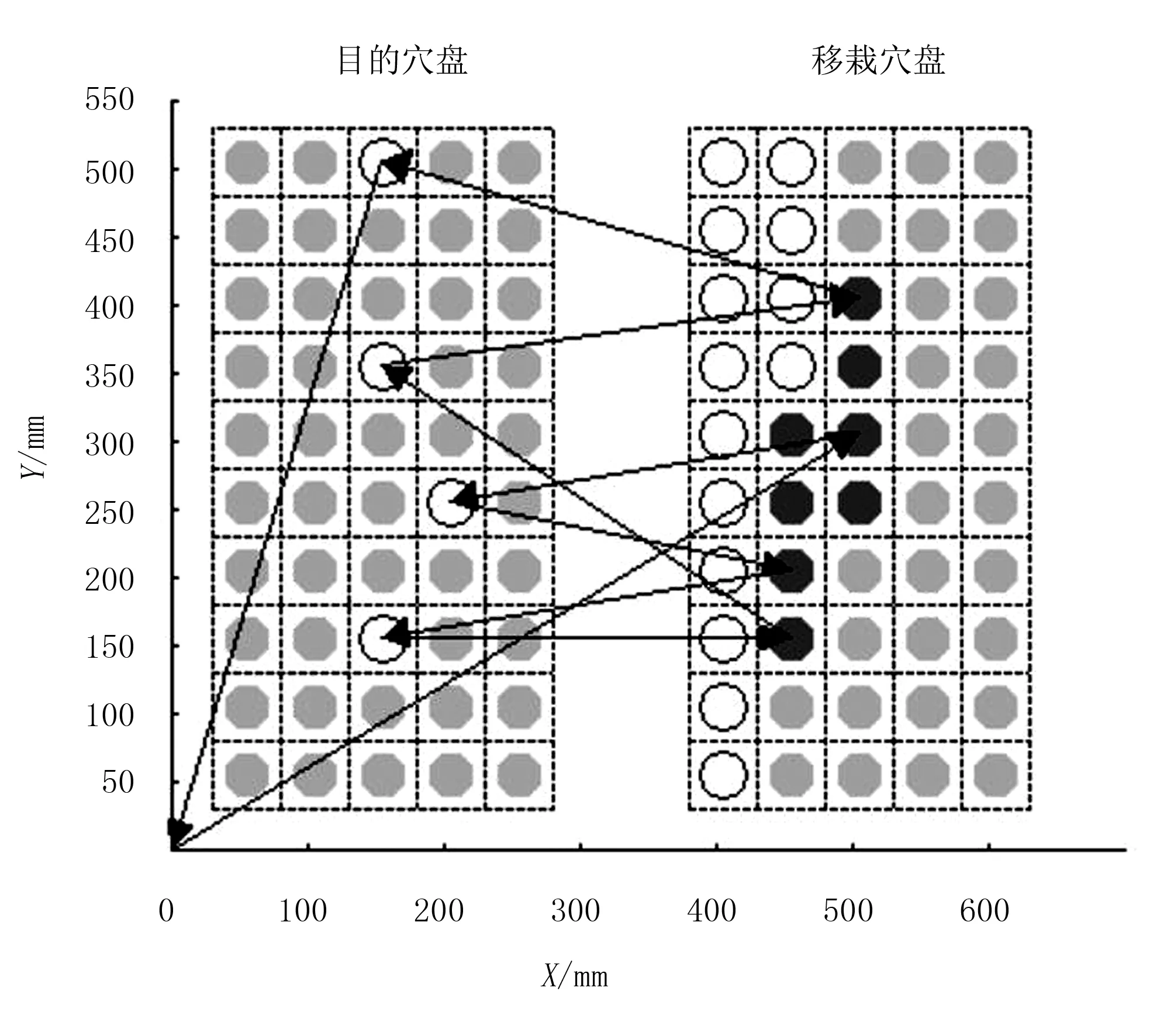
图1 健康钵苗补种移钵作业示意图Fig.1 Healthy seedling plant transplanting diagram

由于移钵路径选择的多样性，本文基于混合蛙跳算法创新自动移钵路径优化新方法，将蛙跳算法的思想有效融入该问题的解决，针对移钵问题提出初始族群的产生、子族群的构建和局部搜索等改进措施。

2.2 基于邻域搜索策略初始化青蛙个体

初始化青蛙个体时，从原点O出发交叉选择移栽穴盘和目的穴盘，直到遍历所有目的穴盘，最终回到原点O。由于移钵问题的特殊性，在选择移栽穴盘序号时采用邻域搜索策略，仅从目的穴盘中待补种穴盘位置的移栽穴盘Neighbor域中进行选择。其中，移栽穴盘Neighbor域包含了移栽穴盘中的各可选择穴盘到目的穴盘中所有待补种的穴盘距离之和最小的前Q个点(M≤Q≤N)。,在图1中，Q=8，填充为黑色的穴孔表示当前目的穴盘的可移栽穴盘Neighbor域，即可选择的移栽穴盘序号限定在集合{1，2，3，4，9，10，11，12}中。图1中的路径即为初始化过程中产生的一条移钵路径。

2.3 子族群构建方法

青蛙群体按照1.1节中的规则划分为若干族群后，为了避免过早陷入局部最优，需在族群内生成一个子族群来进行局部搜索。每个族群中的青蛙个体按照概率Pi被选择生成子族群，则有

(3)

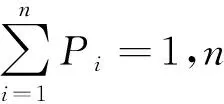
2.4 基于交换序与交叉策略的局部搜索

在子族群中Xb表示局部最优解，Xw表示局部最差解，一个青蛙个体由目的穴盘中的穴孔序号与移栽穴盘中的穴孔序号交叉排列。其中，目的穴盘中的穴孔序号包括了所有的待补种的穴孔位置，而青蛙个体中的移栽穴孔序号仅为部分可移栽穴孔序号。根据青蛙个体的特殊性，将一个青蛙个体分块向局部最优解方向进行搜索。

现针对图1环境来描述局部搜索，待补种穴孔数目M为4，可移栽穴苗数N为36。假设某子族群内Xb={0,1，-1，9，-2，2，-4，4，-3，0},Xw={0，11，-4，3，-3，4，-2，9，-1，0}，Xw如图1中路径所示。将Xb分割为移栽穴孔集合Xbmove={1，9，2，4}和目的穴孔集合Xbgoal={-1，-2，-4，-3}，而Xw分割为Xwmove={11，3，4，9}和Xwgoal={-4,-3,-2,-1}。针对Xb与Xw的目的穴孔集合执行交换操作，移栽穴孔集合执行交叉操作。

2.4.1 交换序

将某个目的穴孔集合的穴孔序号i与穴孔序号j交换的操作定义为一个交换因子，记为CH(i,j)，如，{-1，-2，-4，-3}+CH(-1,-4)={-4,-2,-1,-3}。交换序是由一个或多个交换因子组成的序列。现有{-1，-2，-4，-3}+CH(-1,-4)+CH(-2,-3)+CH(-1,-2)={-4，-3，-2，-1}，则Xwgoal向Xbgoal转换时的交换序为{CH(-1,-4),CH(-2,-3),CH(-1,-2)},记为CS(XwgoalΘXbgoal)，其中交换序的长度为3。

2.4.2 交换操作

将Xwgoal向Xbgoal转换时的交换序CS(XwgoalΘXbgoal)的长度记为Length(CS(XwgoalΘXbgoal))，则Xwgoal向Xbgoal变换时的交换操作可定义为

C= {CHi|CHi∈CS(XwgoalΘXbgoal),i=1,2,…,l}

(4)

Xqgoal=Xwgoal+C

(5)

其中，l为[0,length(CS(XwgoalΘXbgoal))]间的随机整数，C为更新Xwgoal的交换序。若l=0则不执行交换操作，青蛙个体目的穴盘序号不变，即Xqgoal直接等于Xwgoal；否则按照式(4)、式(5)进行交换操作产生新的Xqgoal。

2.4.3 交叉策略

针对可移栽穴孔集合Xbmove与Xwmove在[0，4]之间随机产生一个整数j作为交叉点，若j等于0时不作交叉，若j等于4则两集合互换，否则交叉操作如图2所示。其中，j=2。交叉过程中若新个体出现重复的穴盘序号，则在Neighbor域可选范围内重新随机生成一个新的穴盘序号替换其中一个重复的穴盘序号。

图2 交叉操作Fig.2 Crossover operation

2.4.4 局部搜索

将Xqgoal分别与Xq1move、Xq2move合并后产生两个新青蛙个体，取其中适应度值较大的一个Xnew与Xw比较，若适应度值f(Xnew)大于f(Xw)则更新青蛙个体，否则利用全局最优个体Xg代替Xb重复执行上述交换与交叉操作；若产生的青蛙个体Xnew仍不优于Xw，则根据初始化要求随机产生一个新青蛙个体替换Xw。

2.5 算法流程

基于以上思想，本文算法流程如下：

1)初始化算法参数。设置青蛙个体的种群大小为F，各族群内青蛙个数为n，族群个数为m，子族群内青蛙个数为k，局部更新迭代次数Count，全局搜索迭代次数为Gcount。

2)基于邻域搜索策略初始化各青蛙个体，生成F个可行解，计算其适应度值。

3)按照适应度值降序排列各青蛙个体，并构造m个族群。

4)按照3.3节方法产生子族群，在每个子族群内按照3.4节的方法进行局部搜索。

5)当局部搜索到达一定迭代次数Count，则混合全部族群，根据适应度值更新全局最优个体，Gcount值自动增1。

6)根据Gcount值判断算法是否终止，若否则转3)。最终，全局最优青蛙个体所表示的解即为规划出的移钵优化路径。

3 仿真实验

为了便于比较，采用文献[3-4]中的实例进行一组实验。由于本文算法在青蛙个体生成过程中，针对移钵问题的特殊性采取了邻域搜索策略，搜索空间大大减少，算法性能显著提升。图3的实例中设定Neighbor搜索域大小为8，Neighbor域中的穴孔在图中用填充为黑色的圆圈表示。图3中显示的路径为本文算法获得的最优化路径，路径长度为2 913.892。连续运行10次中9次获得全局最优解，平均路径长度为2 915.6，路径优化结果优于文献 [3-4] 中的结果。

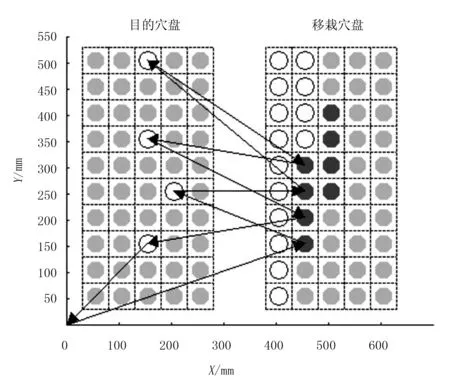
图3 4个待补种穴盘自动移钵路径Fig.3 Path planned with 4 vacancy cells

假设目的穴盘中待补种穴盘个数为10，移栽穴盘与图3中的移栽穴盘一样，如图4所示。在目的穴盘中分10次随机生成10个待补种穴盘，使用本文算法规划出的自动移钵路径长度如表1所示。其中，Neighbor域中的可移栽穴盘数量设置为20。与文献[4]中的固定顺序法和蚁群算法进行比较，可以看出：本文算法较固定顺序法优化比例在8%以上，表1中最后一列优化比例指的是本文算法较固定顺序法优化的比例；同时，本文算法性能比蚁群算法更优(迭代次数均设定为500)。其中，序号为1的蛙跳算法自动移钵路径规划结果如图4所示，收敛曲线如图5所示。从收敛曲线上看，本文算法初始化时产生的全局最优路径为7 780.316，比固定顺序法产生的路径8 189.573已经更加优化。

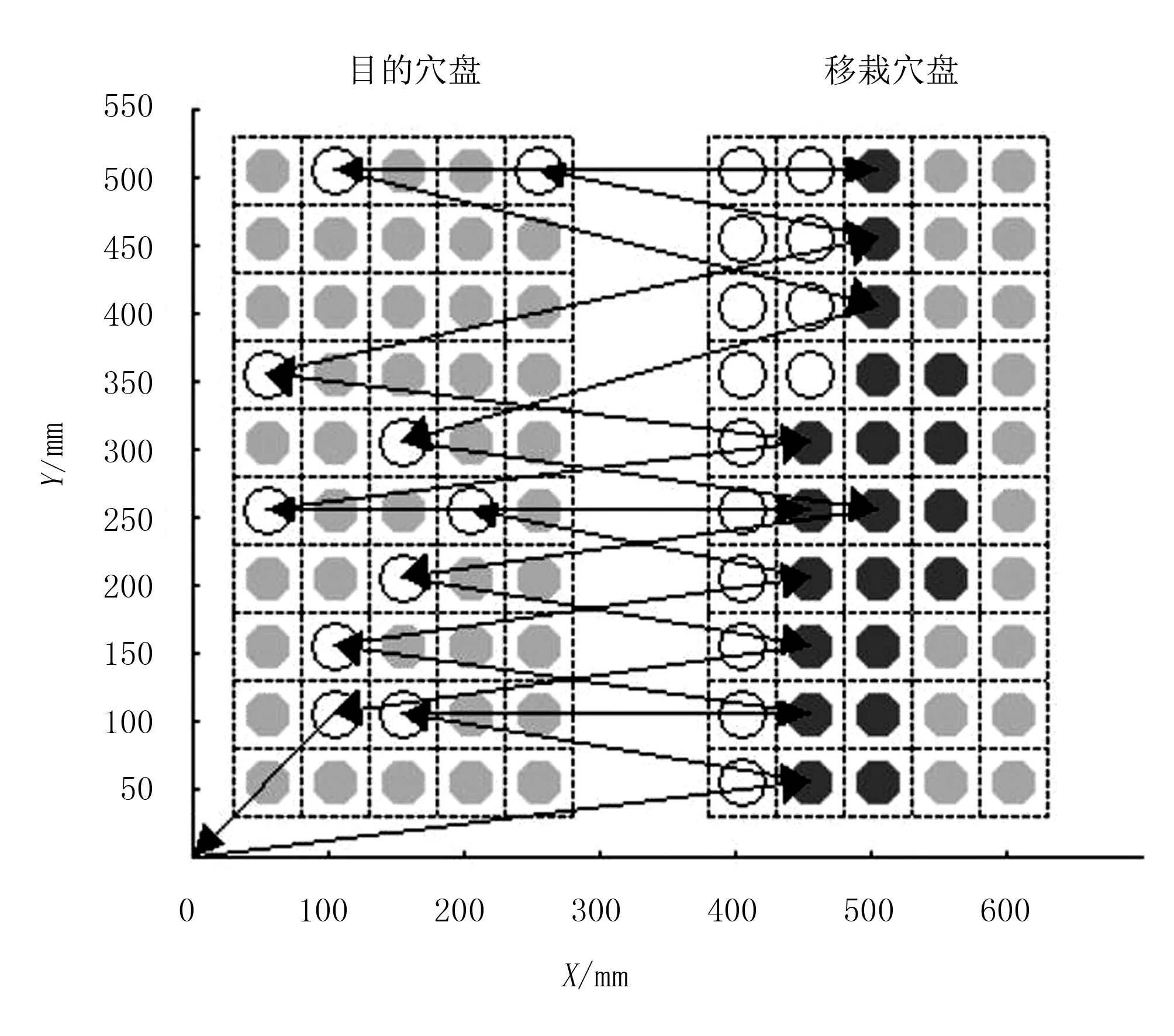
图4 10个待补种穴盘自动移钵路径Fig.4 Path planned with 10 vacancy cells表1 不同算法移钵路径优化长度对比Table 1 Comparison of optimized length of different algorithms

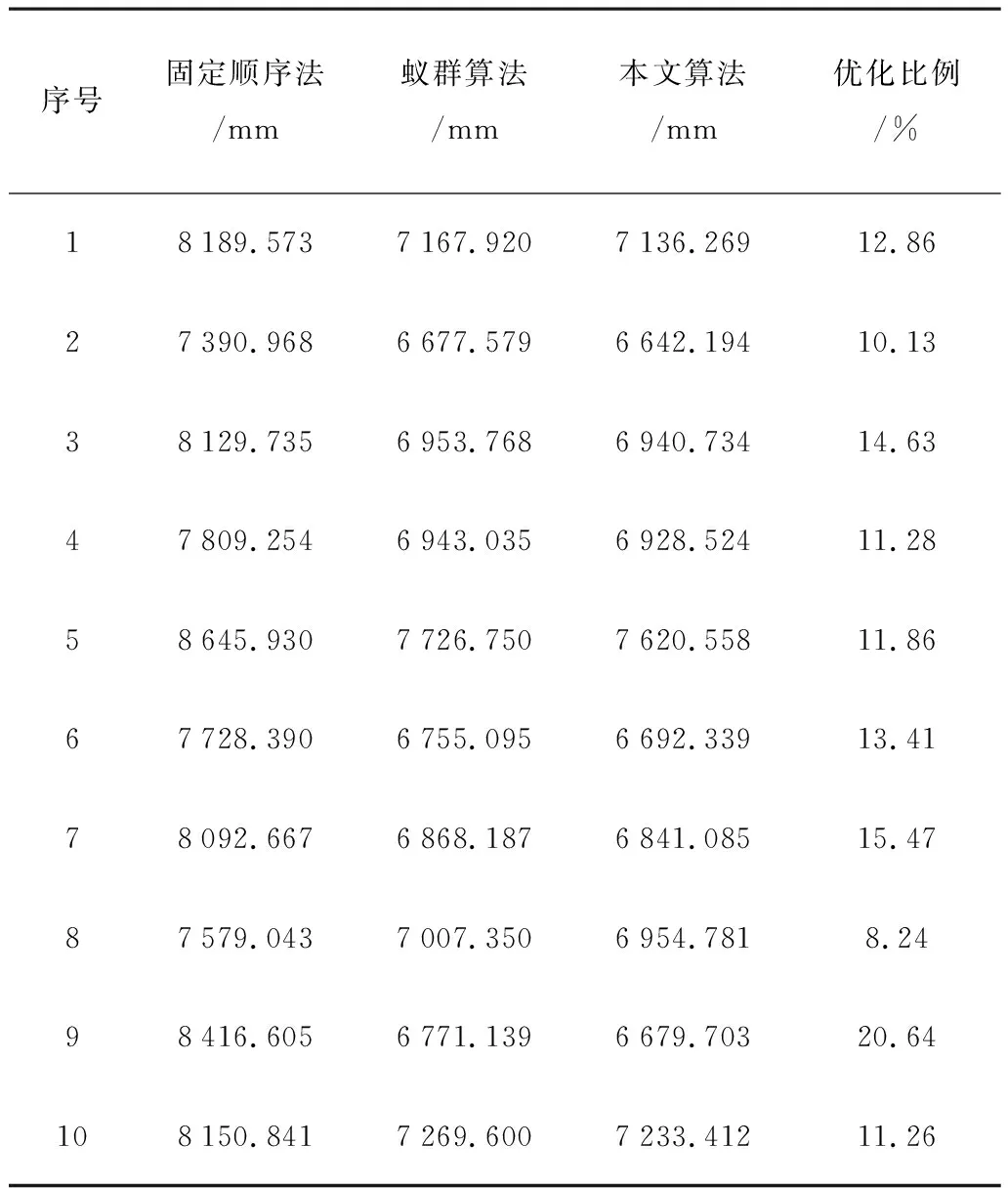
序号固定顺序法/mm蚁群算法/mm本文算法/mm优化比例/%18189.5737167.9207136.26912.8627390.9686677.5796642.19410.1338129.7356953.7686940.73414.6347809.2546943.0356928.52411.2858645.9307726.7507620.55811.8667728.3906755.0956692.33913.4178092.6676868.1876841.08515.4787579.0437007.3506954.7818.2498416.6056771.1396679.70320.64108150.8417269.6007233.41211.26

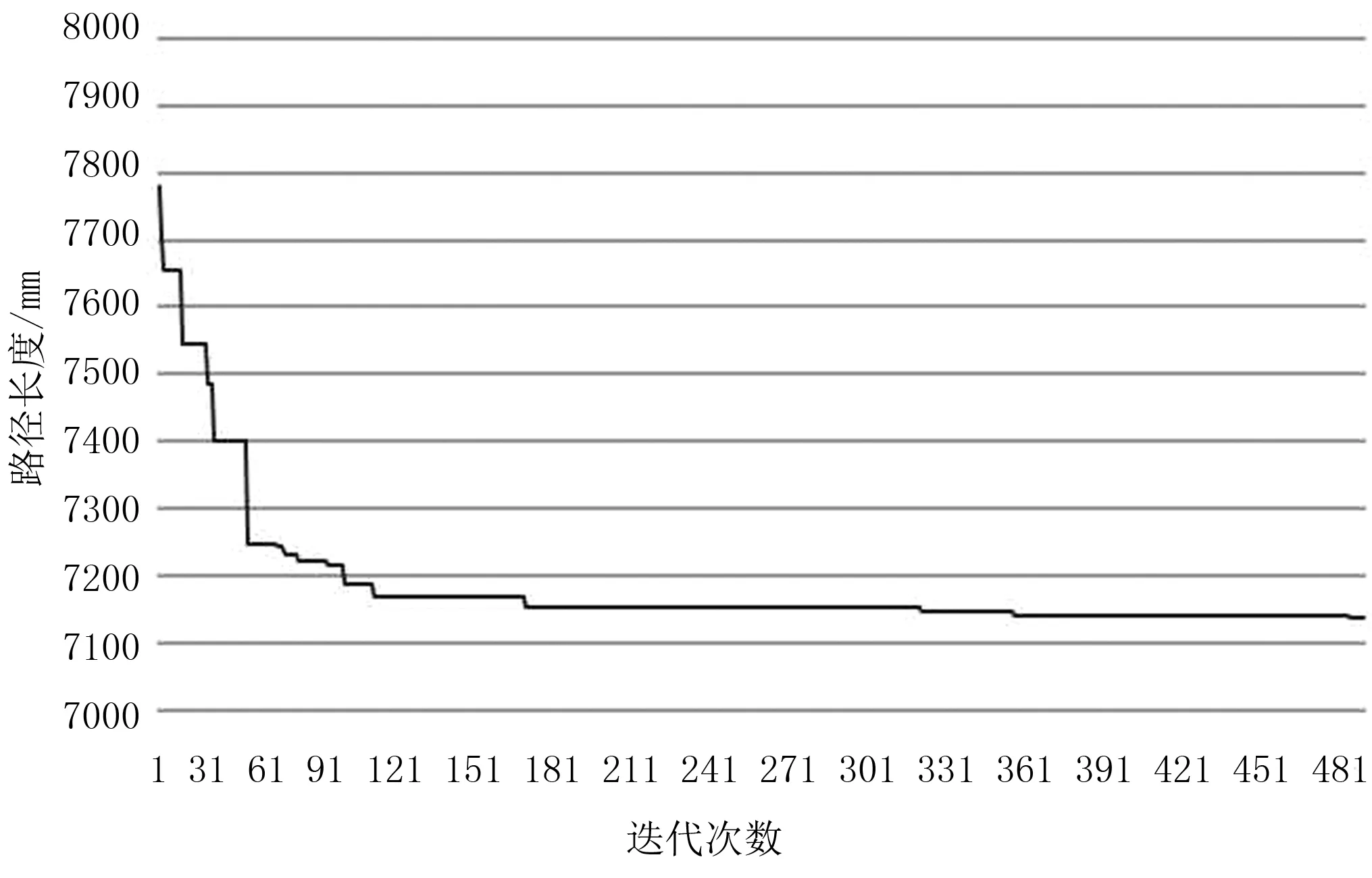
图5 蛙跳算法自动移钵路径规划收敛曲线Fig.5 Frog leaping algorithm automatic path planning convergence curve

4 结论

针对穴盘苗自动移钵路径规划问题，基于混合蛙跳算法提出了融入交换序和交叉操作的局部搜索方法，较好地解决了移钵问题的路径优化问题。本文算法具有鲁棒性好、实时性能强、易实现等特点。本文算法在解的生成过程中引入邻域搜索策略，在一定的邻域内选择移栽穴盘，大大缩小了解的搜索空间，提高了算法性能，与固定顺序法、遗传算法和蚁群算法等相比能较好地获得更优化路径，算法收敛性能好。