基于模糊PID算法的农机自动转向系统研究

王茂励，段 杰，唐勇伟，赵景波，姜 岩

0 引言

我国是一个农业大国，农业人口众多，但农业发展水平与西方的一些发达国家还有着很大差距。随着科学技术的迅速发展，现代农业的发展也在日益兴起，农业机械化程度对农业发展水平的影响正在日益加深。

发展精准农业是实现现代农业的前提，农机的自动导航系统又是精准农业的重要一步，自动转向控制系统又是自动导航系统中的关键一环。在自动转向控制系统中，控制算法的选择、设计及优化的好坏，直接影响农机的作业精度[1-3]。PID控制算法是一种最为常用的控制算法，可以从根本上摆脱系统建模，只需要依据被控对象的一些响应特征来组合控制模块，控制过程简单且稳态性好[4-6]。模糊控制亦不依赖于控制模型，而是根据人们的工作经验，对于被控对象进行简单的模糊处理，但与此同时影响了控制精度[7-8]。

在此基础上，将PID算法与模糊控制巧妙地结合起来，能够互补利弊，会使整个控制系统获得更加良好的性能，增加系统的灵活性和精确性，可在播种或者收割等工作中加以应用[9]。

1 自动转向控制系统构成

农机的自动转向控制系统由导航控制器、转向控制器、转向驱动器、农机转向系统以及转角测量模块几部分组成，如图1所示。其工作原理为：在农机的导航控制系统中计算出农机的目标转角后，通过CAN总线将目标转角的值传递给下位机；转向控制器通过目标转向角和目前车轮的转角差值及转角差值变化率的不同，结合转向控制算法，控制液压驱动器来实时调节比例阀的方向和开度，驱动农机转向系统工作，最终完成农机的自动转向功能[10]。将农机自动转向系统的控制过程用二阶传递函数表示为

(1)

其中，R(s)即目标转角，Y(s)即转向角，e、c、d均为待定参数。

2 模糊PID自动转向控制系统

2.1 PID控制器设计

PID控制算法的表达式为

(2)

u(k)=

其中，k为采样次数；u(k)为第k次采样时输出的值；e(k)为第k次采样时输入的偏差值。由式(3)可以推出

Δu(k)=u(k)-u(k-1)=
KP[e(k)-e(k-1)]+KIe(k)-
KD[e(k)-2e(k-1)+e(k-2)]=
KPΔe(k)+KIe(k)+KD[Δe(k)-Δe(k-1)]

(4)

此时得到的Δu(k)就是增量型PID控制算法的表达式。在采样中，只要确定了ΔKP、ΔKI、ΔKD这3个参数的值，使用3次的测量偏差从而求出控制量的增量。

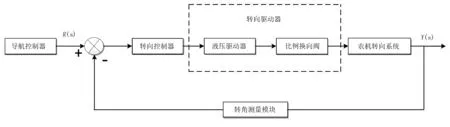
图1 自动转向控制系统结构图Fig.1 Automatic steering control system

2.2 模糊PID控制器设计

模糊PID控制系统的原理就是运用模糊数学的理论和方法，把模糊控制规则以模糊集的形式表示出来，根据被控对象的实际响应情况运用模糊推理，实现对PID参数在不同时间不同状态下的最佳调整，实现最优控制。系统的结构图如图2所示。

图 2 模糊PID控制系统结构图Fig.3 Fuzzy PID control system structure diagram

此设计将模糊PID控制器的输入定为转向角偏差e(t)和偏差变化率ec(t)，输出则为模糊控制器经过模糊规则推理得到的ΔKP、ΔKI、ΔKD。系统在线实时改变的参数的值为KP+ΔKP、KI+ΔKI、KD+ΔKD，实现了PID控制算法中参数的自整定环节。此时，参数模糊自整定PID控制的计算量非常小，并且被控对象的动、静态性能也有所提高。

2.3 模糊控制规则

PID参数自整定的主要思路就是找出PID算法当中的3个参数与转向角偏差e(t)和偏差变化率ec(t)之间的模糊联系。当农机在田间行走时，控制器会不断地检测e(t)和ec(t)的值，且不断地对检测到的值和PID的3个参数进行在线修改，从而满足在不同环境中的e(t)和ec(t)对PID控制器的不同要求。农机的自动转向控制系统的响应输出曲线如图3所示。

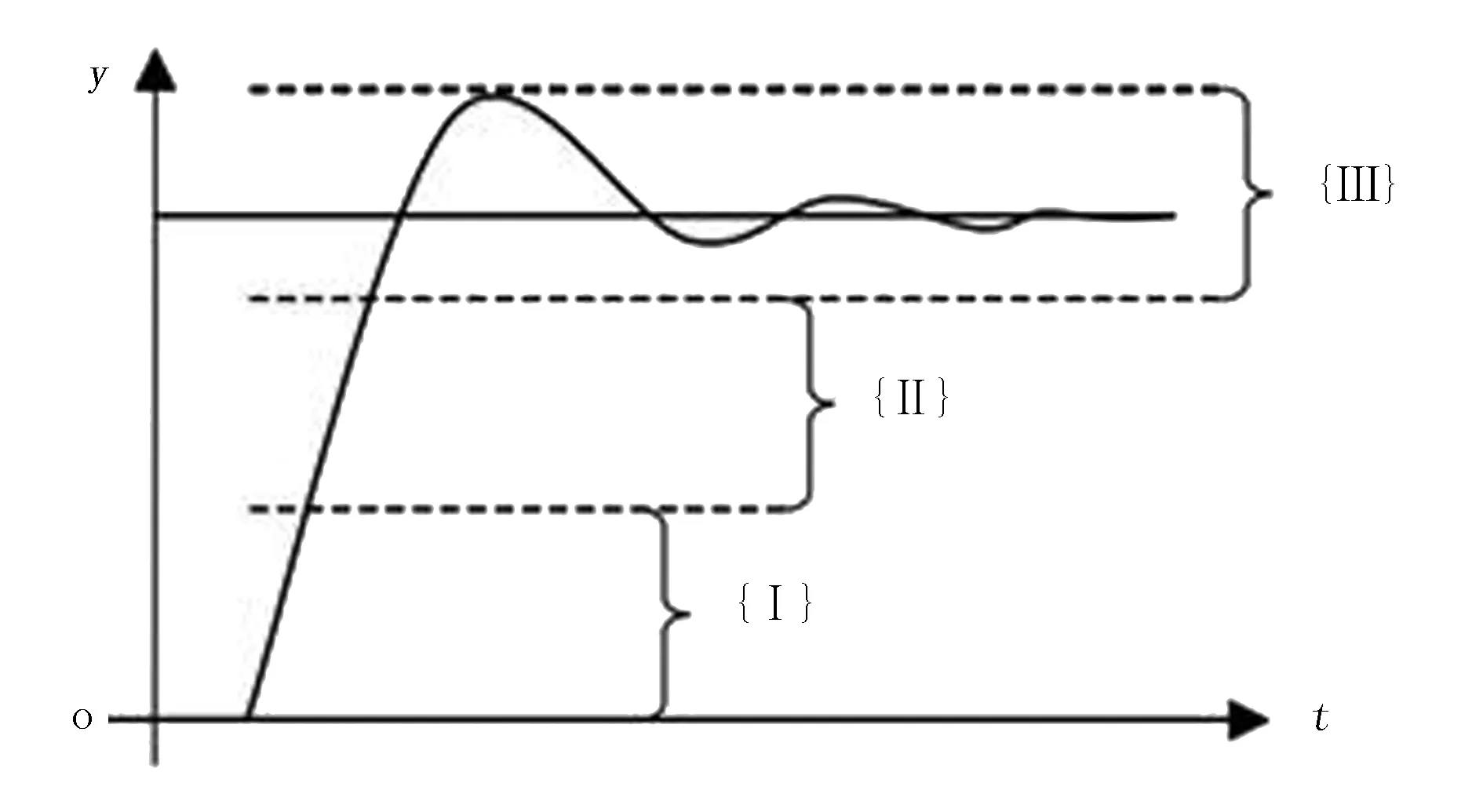
图 3 系统输出响应曲线Fig.3 The system outputs the response curve

分析图3中的响应曲线，可以总结出PID控制算法的3个参数与转向角偏差e(t)和偏差变化率ec(t)的之间联系：

1)当输出响应处于图中曲线的第 I 阶段时，|e(t)|的值较大，为了不让开始时|e(t)|的值瞬间变大，从而导致微分溢出，应该取较大的KP和较小的KD。这样还可以提高转向控制系统的响应速度，还应取KI=0以此来防止积分饱和。

2)当输出响应处于图中曲线的第 II 阶段时，|e(t)|和|ec(t)|的值都是中等大小，为了减小转向控制系统的超调，保证步进电机的响应速度，KP、KI和KD的值都不能取得太大，KP的值要取得较小，KI和KD的值要大小适中。

3)当输出响应处于图中曲线的第 III 阶段时，|e(t)|的值较小，为了使自动转向系统具有良好的稳态性能，应该增大KP和KI的数值。同时，应该适当的选取KD的值，以此来提高系统的抗干扰能力，其原则是：当|Δe(t)|的值较小时，KD的取值要大一些；当|Δe(t)|值较大时，KD取较小的数值。通常KD和KI的值都要取为中等大小。

根据上述分析可以得出：不确定的系统在常规控制作用下，误差和误差变化率e(t)和ec(t)的值越大，系统中的不确定量就越大。那么如果误差e(t)和误差变化率ec(t)越小，系统中的不确定量就越小。利用这个e(t)和ec(t)对系统不确定量的估计，进行对PID3个参数KP、KI和KD的调整计算。

在模糊PID控制器的设计过程中，每个输入输出量e(t)、ec(t)、KP、KI和KD都需进行相应模糊化的处理。其模糊子集为{NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PB(正大)}，根据农机自动转向控制系统的特点，各个子集的隶属函数均选取为高斯型隶属函数，其中心点分别为{-6，-4，-2，0，2，4，6}，如图4所示。

图4 输入输出变量的隶属度函数Fig.4 The membership function of the input and output variables

根据KP、KI和KD3个参数各自的作用以及它们之间的相互影响，建立KP、KI和KD的模糊控制规则表，如表1～表3所示。

根据KP、KI和KD这3个参数的模糊规则表以及每个模糊子集的隶属度赋值表，应用模糊规则来推理设计出的PID参数模糊矩阵表，将修正后的参数带入式(5)～式(7)，来完成对PID参数的在线自矫正。

(5)

(6)

(7)

2.4 解模糊化

通过模糊推理得到的输出是一个模糊的集合，模糊的量是不可以直接控制对象的。解模糊化的过程就是把通过模糊化得到的模糊集转化为确定的控制量的过程[9]。运用合理的转化方法，才能得到准确的控制量去控制被控对象，这里我们采用了重心法，具体方法是先找到模糊隶属函数曲线与坐标轴的横轴所围成面积的重心，然后将这个重心看作成代表点，最后计算出输出范围内几个连续点的重心，即

当输出变量为离散集时，则为

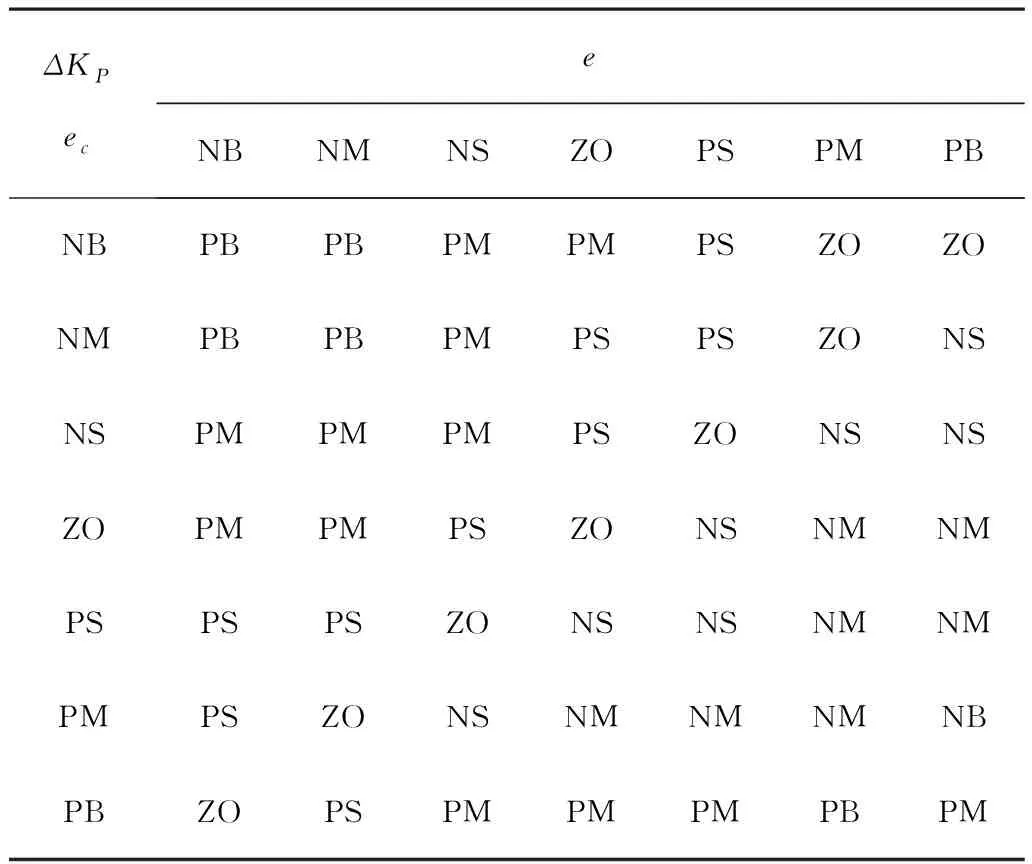
表1 ΔKP模糊控制规则表Table 1 ΔKP fuzzy control rule Table

表2 ΔKI模糊控制规则表Table 2 ΔKI fuzzy control rul Table

表3 ΔKD模糊控制规则表Table 3 ΔKD fuzzy control rule Table

3 系统试验与仿真与分析

3.1 系统试验平台

系统试验在山东省临沂市郯城县育新合作农场中进行，试验平台为东方红LX1204型拖拉机，如图5所示。试验将自动导航控制系统安装在东方红拖拉机上，为了在拖拉机转向时得到精确的数据，将拖拉机的前轮支起腾空，这样便消除了转向时与地面产生的摩擦力，从而会更加直观准确的观察其特征。

图5 东方红LX1204型拖拉机Fig.5 Oriental red LX1204 tractor

3.2 仿真结果与分析

由图6可以看出：采用模糊PID的控制方法控制农机的转向会使转向系统的整个动态性能得到显著的改善。

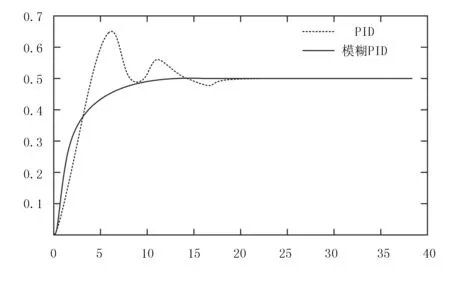
图6 系统仿真响应曲线Fig.6 System simulation response curve

根据表4可以看出系统的响应时间明显缩短一倍以上，另外还对转角进行了实验。通过上位机向转向控制器输入不同的目标转向角控制指令，可以看出模糊PID控制算法能够更快的控制拖拉机的自动转向，能够更加精确的保证目标角度在±1°以内。

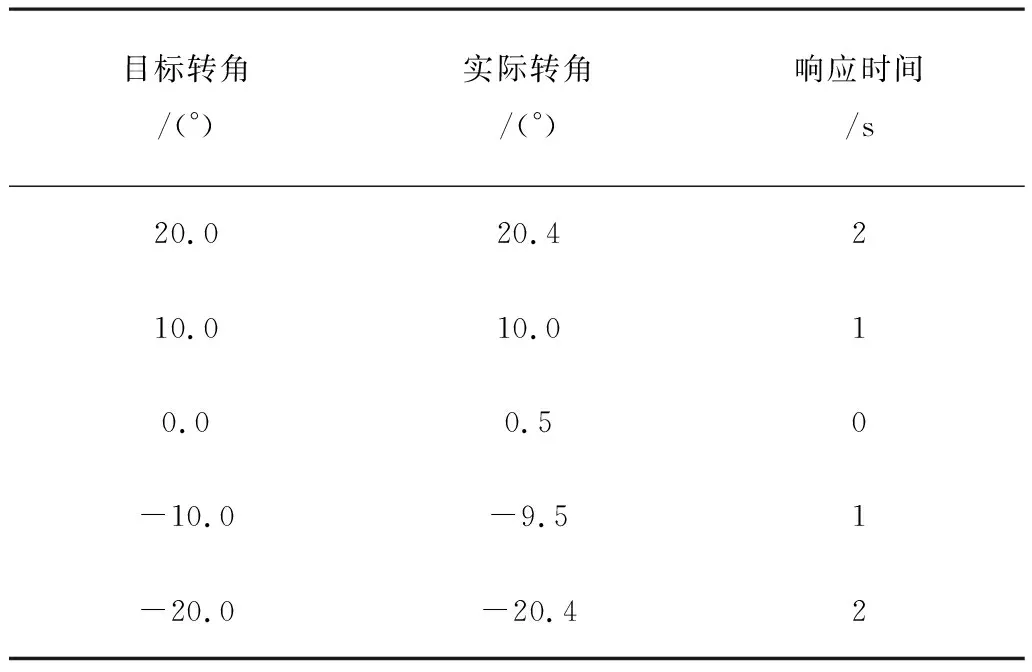
表4 转角实验结果Table 4 Corner test results

4 结论

设计了一种基于PID控制算法的模糊PID控制器，并且将其运用到农机的自动转向控制系统上，较好地结合了两种算法的优势使转向控制系统更加稳定。在实物试验时，运用东方红拖拉机进行实物的演示，在MarLab的仿真过程中，分别将在PID控制下和在模糊PID控制下的相应曲线进行对比，在转角试验中输入不同的目标值对农机的转角及响应时间进行记录和分析。结果表明：此控制方法能够在满足农机控制要求的基础上将其优化，具有更好的快速性和准确性，响应时间更短，稳态误差更小，是一种可靠且优良的控制方法。