地月低能轨道转移的混沌控制方法

郑 越，泮斌峰，唐 硕

(1. 西北工业大学航天学院，西安 710072；2. 陕西省空天飞行器设计重点实验室，西安 710072)

0 引 言

三体模型下航天器轨道常常呈现混沌运动状态。利用混沌的遍历特性，能够使航天器在不耗能的情况下飞行到想要的合理位置。但由于混沌运动本身具有内在随机性和长期趋势不可预见性，导致航天器在混沌区域的滑行时间过长。因此，在利用三体模型下混沌运动低能量特性的同时，如何有效减少轨道转移时间是实现大规模、低成本探月活动的迫切需求，对探月工程的发展具有非常重要的意义。

目前采用混沌控制理论设计轨道的研究尚处于起步阶段。1995年，Bollt等[1]基于庞加莱截面对流形进行多次截断来实现地月低能转移，有效地减少航天器在混沌区域的滑行时间，转移过程中施加了8次脉冲。随后，Schroer等[2]通过对一组不稳定周期轨道进行打靶，利用比Bollt的方法略高的能量缩短了地月转移时间，转移过程中需要至少4次脉冲。Macau[3]将从地球和月球附近出发的轨道进行拼接，通过3次脉冲，进一步用能量的增加换取了地月转移时间的缩短。近期，Salazar等[4]发展了Bollt方法[1]，通过增大庞加莱截面流形截断约束值，利用更大的能量和8次脉冲，以更短的时间到达月球；此外，借助于月球引力辅助变轨方式，也将混沌控制拓展至到地月三体系统L4,L5拉格朗日点的低能转移任务。

为了减小地月转移过程中所需要的能量，现有的混沌控制方法[1-4]都利用了轨道在庞加莱截面图上的投影点的稳定方向与不稳定方向的交点，分别采用了同一轨道截断[1,4]和不同轨道拼接[2-3]的方法。对于同一轨道截断的方法，需要轨道本身存在位置接近的投影点。而每次截断需要在轨道转移过程中施加两个脉冲，导致轨道转移过程所需要的脉冲过多。即使减小庞加莱截面流形截断约束值以保证低能耗转移，轨道转移所需要的时间也较长。对于不同轨道拼接的方法，通常需要利用周期轨道作为中间轨道[2]而实现，具有依赖性。

针对现有混沌控制方法存在的需要脉冲次数多和必须通过固定周期轨道等缺点，本文提出一种新的低能地月轨道转移方法。该方法针对地月三体系统中混沌运动的内在随机性，将混沌区域在庞加莱截面图上进行分层。进一步分析航天器在混沌区域各层之间的运动趋势，找到了在尽可能减少飞行时间的前提下完成地月轨道转移的途径。通过粒子群算法确定地月转移轨道通过L1瓶颈区的状态点，利用向前-向后法在尽可能减少飞行时间的前提下通过2～4次脉冲实现地月低能轨道转移。

1 地月三体系统

1.1 动力学模型

考虑地月圆型限制性三体问题(Circular restricted three-body problem，CRTBP)，质量可以忽略的航天器在地球和月球两个主天体的引力作用下的运动，其中主天体绕其公共质心做匀速圆周运动[5-6]。归一化地球质量m1和月球质量m2之和为单位质量，则：

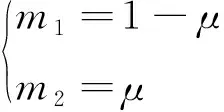
(1)

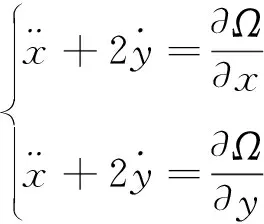
(2)

其中，Ω为旋转坐标系下的等效势能：

(3)

设r1,r2为航天器到两个主天体的距离，有：

(4)

CRTBP系统中，存在雅可比积分如下：

(5)

在地月三体系统中，单位长度为地月之间的距离，L=3.844×105km，单位时间为T=104 h，单位速度为V=1024 m/s。

1.2 庞加莱截面图及分层

图1为地月三体系统中雅可比能量C=3.17948的庞加莱截面图，E，M分别表示地球和月球。以平动点L1[11]为分界线，将庞加莱截面区域分为地球引力区和月球引力区。在地球引力区中存在四组稳定的KAM环，分别用Ⅰ,Ⅱ,Ⅲ,Ⅳ表示。本文利用KAM环对庞加莱截面地区引力区中的混沌区域进行分层。首先绘制第Ⅱ, Ⅲ, Ⅳ组KAM环的包络线，形成的封闭区域分别为2个，3个和1个。然后将第Ⅲ组KAM环靠近地球一端的包络线相连，靠近月球一端的包络线与第Ⅳ组包络线靠近月球一端的边缘连接，则可以定义第Ⅲ组KAM环和第Ⅳ组KAM环的包络线之间的区域为C层。最后将第Ⅱ组KAM环靠近地球一端的包络线相连，靠近月球一端的包络线以其边缘的曲度延伸并将庞加莱截面地球引力区分为两个部分，定义靠近地球部分的混沌区域为A层，而靠近月球部分C层以外的混沌区域为B层。

2 混沌控制在低能地月轨道转移中的应用

混沌系统具有内在的敏感性，表现为对系统施加小的扰动，会使系统偏离固有轨迹而运动[12-13]。这个扰动可以非常小，不改变系统动力学特征，而驱使固有的系统动力学到最终想要的状态。这个混沌控制的过程也被称为目标命中[14]。由于在混沌系统中，微小的扰动能够导致巨大的终端状态偏差，混沌控制的目的就是确定何时以及如何选择微小的扰动来达到预期的终端状态。在地月三体系统中，混沌控制的目的就是通过微小扰动产生的能耗改变航天器轨迹以尽可能缩短飞行时间。

本文根据地月系统庞加莱截面图上轨道投影点的分布情况，进一步提出了地月轨道转移时间优化原则。利用向前-向后法，在节省时间的前提下，拼接出地月低能转移轨道。

2.1 地月轨道转移时间优化原则

航天器在地月三体系统下不耗费任何能量的轨道转移可以认为是在地球引力区域的滑行过程中受到月球小引力的影响，与地月之间连线的相交位置逐渐向月球靠近，最终滑行至月球引力区而到达月球附近的过程。由于在航天器的滑行过程中会经过混沌区域的很多层，而过多的混沌层和在每一层内过长的游荡时间，是地月轨道转移时间过长的主要原因。因此要减少地月轨道转移时间就要让航天器只经过必经的混沌层并且尽可能减少在每一层的游荡时间。

图1为地月三体系统中雅可比能量C=3.17948的庞加莱截面图。由地月CRTBP三体动力学模型的公式(2)可以得出，在每个主天体的引力区，离主天体距离越远，航天器可以达到的最大速度越小。航天器在地月系统的地球引力区的滑行过程是一个在动能作用下远离地球，而在地球引力作用下速度逐渐变小而再向地球附近滑行的一个往复过程。一旦航天器动能可以克服地球引力，航天器将穿过L1瓶颈区域并受月球引力作用从而到达月球附近。而庞加莱截面图的包络线可以认为是航天器在离主天体相应距离下可以达到的最大速度，可以直接影响航天器滑行时的轨迹形状。

第1.2节中分析了地月轨道初始位置的选择原则，即应该从轴上第Ⅰ组KAM环的右侧开始向月球方向移动。图2为初始位置从第Ⅰ组KAM环的右侧向月球方向过渡的一组周期轨道(圆圈表示周期轨道的初始位置)；图3为地月系统的庞加莱截面图。图2中的周期轨道图2(a),2 (b),2 (c), 2(d),2 (e), 2(f) ,2 (g),2 (h)在图3中的投影点分别对应于周期轨道a, b, c, d, e, f, g, h。图3中，投影点位于KAM环圆心的周期轨道f为稳定周期轨道，对其周围轨迹流形具有吸引作用；而投影点位于混沌区域的周期轨道a, b, c, d, e, g, h为不稳定周期轨道，可以作为三体系统下轨迹流形状态随着初始点变化的分析依据。将图3中的周期轨道与图1中混沌区域的分区图相对应，周期轨道a, b在A层中，通过A层在庞加莱截面图上所处的位置可知轨道流形在A层内距离地球近且速度较大，流形远离地球再回到地球附近的一个过程中轨迹流形如轨道a, b形成交叉点。同时，A层中的周期轨道随着初始位置的改变，会经过一系列如轨道b的过渡而进入B层，演变为图2(c)中周期轨道的形状(图2(c)中周期轨道为文献[2]中规定的中间目标)。在B层中，航天器远离和靠近地球的一个往复过程与地球的距离显著增大，轨道形状也如图2(d), 2(e)发生了很大的变化。而在B层内航天器已经可以脱离地球引力的束缚而进入月球引力区，如图2(e)所示。当轨道在庞加莱截面图中处于以周期轨道f为中心的KAM组的内圈即C层时，航天器远离和靠近地球的一个往复过程与地球的距离进一步增大，且在C层内航天器非常容易滑行至月球引力区。图2(h)为轨道从C区向月球附近转移的流形图。

通过图2(a), 2(b), 2(c), 2(d),2(e), 2(f), 2(g),2(h)可以演变出航天器从地球附近向月球附近轨道转移的过程。转移轨道在混沌区域的过渡过程可以通过A→B→C或者A→B。为了节省转移时间，轨道应该通过A→B转移至月球附近，所以轨道经过C层是轨道转移耗时过长的一个重要原因。轨道转移耗时过长的另一个原因是轨道流形会在相邻两层之间来回滑行。如图2(g)所示，其轨迹在庞加莱截面图3上的投影g在B, C层之间滑行会消耗过多的飞行时间。所以，为了节省地月轨道转移时间，就是要使航天器尽快从A层滑行至B层然后再滑行至月球附近，且避免轨道流形在两层之间来回滑行。

2.2 地月轨道拼接方法

地月系统的混沌区域内，在初始端施加小的扰动可以使轨迹终端的状态发生很大的变化，而混沌本身具有遍历性，可以在初始端速度改变很小的前提下使航天器轨迹遍布广泛区域，通过两条轨迹的拼接来实现轨道转移。

轨道间的拼接是一个目标命中的过程，可以用Shinbrot等提出的向前-向后法(Forward-backward method)来实现[15]。算法的思想如图4所示，为了找到从初始状态点进入以εt为半径的目标域的一段轨迹，对以(p0,q0)为中心长度为δ的控制段(p,q)施加控制(p,q分别为位置和速度)并向前迭代，而小的目标域向后迭代，如果存在一条同时通过初始位置附近和目标区域的轨迹，则控制段和目标区域的延展方向将最终相交，从交点演变到控制段的点pint出发可以直接到达目标区域。

由于在轨道转移过程中施加脉冲只能改变航天器的速度，不能改变其位置，本文将庞加莱截面图上地球附近的初始点P为中心的区域作为目标域，而控制段上状态点位置坐标位于L1瓶颈处，横向速度的大小由长度为δ的线段确定，且控制段上所有状态点速度大小相同。目标域不稳定方向上的点正向时间积分会逐渐远离以P为初始点的轨迹，控制段稳定方向上的点反向时间积分会逐渐远离以控制段中心点为初始点的轨迹。目标域和控制段经过数次迭代后，其延展方向在庞加莱截面图上相交，通过交点反向时间和正向时间积分，可以得到一条从P点附近出发到达L1瓶颈的一段轨迹。由于尽可能缩短航天器在混沌区域的运送时间是地月轨道转移的重要目标，应该尽量减少控制段和目标域的迭代次数。当控制段与目标域迭代过程中位置很近，延展方向又几乎平行不易存在交点时，可以通过一个脉冲来拼接轨[16]。

2.3 控制段的确定方法

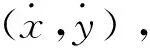
在PSO算法中，有m个n维的向量的粒子组成一个种群，每个粒子对应一个位置向量和一个速度向量。每个粒子根据自己的飞行经历和种群中其他粒子的飞行经历来调整自己的飞行，通过跟踪个体最优粒子和全局最优粒子来控制自己的运动。在粒子寻优过程中，第i个粒子第s维向量的运动轨迹描述如下：

(6)

式中:c1和c2为学习因子，是非负常数，r1s和r2s服从[0,1]上的均匀分布的随机数，vis是粒子的速度，pis为局部最优位置，是第i个粒子迄今为止搜索到的最优位置，pgs为全局最优位置，ω是惯性权值。

本文算法中，控制段中心点的候选状态点向量与每个粒子的二维位置向量(y,θ)相对应，y表示状态点在纵坐标上的位置，在固定雅可比积分下，该点的速度可以通过式(5)得到：

(7)

θ表示状态点速度的方向，则：

(8)

由第2.2节可知，轨道可以通过目标域和控制段的延展方向在庞加莱截面图上的交点完成拼接。将目标域数次迭代后形成的区域定义为拼接区域F，本文根据轨迹与F区的最短纵坐标距离计算粒子适应度值，方法如图5所示。轨迹从每个状态点出发，如果在预定时间TM内，正向时间积分能够到达月球附近，在预定时间TF内，反向时间积分不经过C层，则将反向时间积分的轨迹在庞加莱截面图上的投影点与区域F最短的纵坐标距离作为这个状态点所对应粒子的适应度值；否则将该粒子的适应度值设定为最大值。计算每个粒子的最小适应度值找出局部最优位置和全局最优位置，最后得出的全局最优位置即为控制段中心点对应的状态向量。

2.4 地月轨道转移设计方法

通过地月三体系统中混沌区域分层和轨道在各层间转移的规律能够得到尽可能快的实现地月轨道转移的途径；向前-向后法可以尽可能地减小地月轨道转移过程中所需要的能量。将这两种优点相结合，能够在节省时间的前提下，有效实现低能地月轨道转移。

为了尽可能减少轨道转移所需要的时间，一方面，目标域正向时间积分并记录每次迭代在庞加莱截面图上的投影点，当迭代N次时如果有部分投影点能够离开A层，则将这些投影点组成的区域设定为拼接区域F；另一方面，从控制段出发的参考轨道正向时间积分可以接近月球附近的KAM 环Q，反向时间积分不经过C层且尽可能快地到达拼接区域F。通过向前-向后法将目标域和控制段的延展方向在区域F进行拼接。目标域内地月轨道转移的起始点通过拼接点反向时间积分得到，而控制段上的转移点通过拼接点正向时间积分得到。地月轨道转移过程如图6所示。

在整个地月转移过程中，本文方法所需施加的脉冲为2～4次。必要的两次脉冲为航天器脱离地球附近周期区域和进入月球附近周期区域所施加的。在控制段和拼接区域F的脉冲可以根据不同情况而改变。在控制段，如果从转移点正向时间积分能够达到月球附近，则地月轨道转移完成，否则在转移点施加冲量转变为控制段中心点，再完成地月轨道转移。在拼接区域，如果目标域和控制段的延展方向在区域F相交，则这段轨迹的拼接不需要施加冲量，否则在庞加莱截面图上选择控制段与区域F横坐标相同，纵坐标距离最近的点进行拼接，施加冲量的大小由纵坐标间的距离决定。

3 数值仿真校验

地月轨道转移就是对地球附近的周期轨道上的航天器施加脉冲，使其飞行至月球附近，然后再对其施加脉冲使其绕月飞行。在地月三体系统中，地月转移轨道的初始点选择与文献[1-4]相同的P点。该点位于半径为59669 km的围绕地球旋转的圆轨道上，在图3所示的庞加莱截面图中用‘*’表示。在雅可比能量C=7.17218时航天器通过P点围绕着地球做周期运动(由于参数精度选择有差异，本文所得到的周期轨道雅可比能量与文献[1-4]中的C=7.1738不一致)，施加一个平行的脉冲使航天器进入混沌区域，这时系统的雅可比能量为C=3.17948(实现地月轨道转移的必要条件是系统雅可比能量必须小于CL=3.1883)。这要求速度的改变ΔV=748.06 m/s(文献[1-4]中ΔV=744.4 m/s)，而如图3所示，点P在C=3.17948时包围在混沌区域内，当轨道转移到月球附近并距离绕月周期轨道为中心的KAM环Q距离很近时，便可以通过一个很小的脉冲使轨道流形进入KAM环的边缘而绕月运动。

当系统雅可比能量C=3.17948，航天器在不施加外力的情况下从庞加莱截面图上的P点滑行到月球附近需要27年多的时间，而且航天器并没有长时间停留在月球附近，而是在月球附近飞行数圈后便很快远离。图7(a)为航天器在系统雅可比能量C=3.17948下从P点自由滑行的轨迹，图7(b)为其对应的庞加莱截面图，对应图1中庞加莱截面图的分区。可以看出，航天器在庞加莱截面图中的A层游荡很长时间后，其轨迹转变为在A层和B层之间飞行；然后经过相当长的时间，转变为在B层和C层之间飞行；最后通过C层轨迹转移到月球附近。

本文选择P点为中心的区域作为目标域，用本文方法确定控制段，规定预定时间TM和TF，进而得到地月低能转移轨道。令TM=5T，图8(a)，图8(b)分别为预定时间取TF=50T和TF=25T得到的两种转移轨道。图8(a)中，航天器从距离P点非常接近的P1点出发，施加ΔVP1=736.3 m/s的脉冲使航天器进入混沌区域。在控制段需要ΔVB1=0.002 m/s，使从B1出发的流形与从P1出发的流形拼接形成地月转移轨道。在离绕月准周期轨道KAM最近的点A1施加一个速度增量使轨道流形进入KAM环内需要ΔVA1=4.6 m/s。将这3个脉冲相加，可得到在混沌轨道的控制中所需要的总能量为740.9 m/s，飞行时间为303天。图8(b)中，航天器从距离P点非常接近的P2点出发，施加ΔVP2=752.4 m/s的脉冲使航天器进入混沌区域。在控制段需要ΔVB2=0.2 m/s，使从B2出发的流形与从P2出发的流形拼接形成地月转移轨道。在拼接点C2需要ΔVC2=141.6 m/s，在离绕月准周期轨道KAM最近的点A2施加一个速度增量使轨道流形进入KAM环内需要ΔVA2=2.9 m/s。将这4个脉冲相加，可得到在混沌轨道的控制中所需要的总能量为

897.1 m/s，飞行时间为184天。与现有文献相比，通过本文方法实现地月轨道转移所需的脉冲次数较少，具体的轨迹可以根据转移过程中需要的总能量和飞行时间的要求来选择。表1为文献[1-4]与图8中轨道所需总能量、转移时间和脉冲次数的对比。与文献[1-4]相比，图8(a)中所设计的轨道使用最小的能耗得到了飞行时间较短的转移轨道，而图8(b)中所设计的轨道通过稍大的能耗显著缩短了飞行时间。

表1 地月轨道转移所需的总能量、飞行时间和脉冲次数Table 1 Required energy, time of flight and impulse times in Earth-Moon orbit transfer

4 结 论

本文通过将地月三体系统的庞加莱截面图分为不同的层，得到了地月系统在实现地月转移轨道时耗时过长的原因，提出地月轨道转移时间优化原则。结合向前-向后法，将从地球附近目标域正向时间积分的轨迹和L1瓶颈处的控制段轨迹进行拼接进而完成低能地月轨道转移。该方法仅需施加2～4次脉冲，在尽可能节省能量的情况下，有效地减少了航天器在混沌区域的滑行时间。而转移所需的能耗和时间的折衷标准是进一步需要完成工作。