多目标多约束组合体与飞船轨道维持优化

陈莉丹, 谢剑锋, 李俊峰, 郝大功

(1. 清华大学航天航空学院，北京 100084；2. 北京航天飞行控制中心，北京 100094)

0 引 言

我国的交会对接任务飞行过程按时间顺序包括飞船起飞入轨段、远距离导引段、近距离导引段、平移靠拢段、对接段、组合体运行段、撤离段、返回准备段和返回段。其中，组合体运行段是指飞船与天宫对接锁紧后,飞船的制导、导航与控制(GNC)分系统停止工作，完全由天宫控制,直到飞船与天宫解锁分离。撤离段是指飞船与天宫解锁开始到飞船撤离至安全距离为止。返回准备段是指飞船撤离之后直至返回制动开始。组合体运行段、撤离段、返回准备段是交会对接任务的重要阶段，期间要进行各种空间技术实验，还要为飞船安全返回地面提供必要的轨道条件。所以，为了确保科学实验顺利进行和飞船安全返回，需要研究组合体运行段、撤离段、返回准备段的轨道维持联合规划方法。

航天器轨道维持目标与具体航天任务要求紧密相关，不同任务会对轨道维持提出不同的要求，一般包括地面轨迹维持、轨道高度维持、轨道构型维持等。文献[1-5]主要针对卫星地面轨迹保持问题进行了探讨，文献[6-7]针对太阳同步轨道卫星和超低轨道卫星研究了轨道高度和偏心率的协调控制，文献[8-11]研究了近地卫星星座的构型保持问题，文献[12-13]设计了卫星在平动点的轨道维持方法。

交会对接任务对不同阶段的多个轨道特征参数提出了要求，文献[14]针对神舟八号、九号任务，解决了地面轨迹、指定点高度及偏心率三个特征参数的控制问题，在神舟八号至神舟十号任务中得到了成功应用。神舟十一号任务与以往交会对接任务相比，轨道维持控制存在以下不同点：一是控制目标在满足返回升交点、制动点高度和撤离点轨道偏心率要求的基础上，新增了对制动点速度倾角的要求；二是组合体在轨飞行时间长达30天，使轨道偏心率控制难度增大；三是天宫二号伴星的存在，使得在撤离返回段，飞船、天宫、伴星的相对运动关系复杂，需要规避碰撞风险。这些都增加了组合体与飞船轨道维持规划的难度，文献[14]设计的策略已不能适应。本文结合神舟十一号任务需求，建立了多目标特征参数的控制方程；提出了通过两次组合体与飞船联合规划来满足不同约束的控制策略；研究了结合规避控制的飞船双脉冲维持优化控制方案；最后设计算例验证了该方法正确有效。

1 问题描述

我国的交会对接任务标称轨道设计为近圆回归轨道，神舟八号至十号为高度约343 km的2天回归轨道，神舟十一号为高度约393 km的3天回归轨道。标称轨道可以使地面轨迹定期重复，同时每个回归周期轨迹严格通过主着陆场，这样的设计便于安排正常及应急落区，最大程度上保障航天员正常或中途应急返回的要求。但由于初始轨道偏差以及各种摄动影响，使得实际飞行轨迹偏离标称值，需要轨道维持控制来消除轨迹偏差。

飞船返回采用标称弹道制导，如果制动点参数与标称状态相差较大，将严重影响返回品质，威胁航天员安全，所以对制动点轨道参数有严格的要求。神舟十一号任务标称轨道高度抬高了约50 km，为了与返回航程相适应，除制动点高度外还新增了对制动点速度倾角的要求。

另外，交会对接任务中飞船与天宫接近或分离时，自主控制使用近圆轨道相对运动方程，这要求飞船对接和撤离时轨道偏心率尽量小。其中，对接点轨道偏心率由天宫初始轨道控制，撤离点偏心率则由组合体段的轨道维持来实现。神舟十一号任务组合体运行长达30天，摄动引起轨道平根数偏心率的周期变化表现明显，偏心率控制难度增大。

最后，神舟十一号任务增加了天宫二号伴星飞行控制，伴星释放后完成对组合体的飞越、驻留等实验，在组合体后方一定距离处等待，待飞船返回后伴星重新追赶捕获天宫。在飞船撤离后，会形成飞船、天宫和伴星三目标的近距离飞行，期间还有飞船撤离脉冲、飞船双脉冲轨道维持等控制，相对运动状态比以往任务更加复杂，存在碰撞风险，可能威胁到航天员的安全。所以，撤离返回段的轨道维持要保证各个目标之间的安全距离。

综上所述，神舟十一号任务组合体运行和飞船返回准备段的轨道维持是一个多目标多约束的优化控制问题。控制优化的目标有：

1)组合体运行要求轨道为近圆轨道，撤离时刻轨道平根数偏心率小于0.001。

2)飞船返回圈地面轨迹与标称一致，返回圈升交点目标为37.7°。

3)飞船返回制动点位于南半球纳米比亚测控弧段内，要求轨道高度393 km，速度倾角-0.05°。

控制优化的约束主要有测控约束和安全性约束：

1)在控制优化时考虑测控约束，即要求组合体及飞船维持控制在地面或中继测控弧段内。

2)撤离和返回准备阶段，三目标相对距离要求满足安全门限20 km，且至飞船返回时刻，伴星距飞船和天宫的距离不小于100 km。

2 多目标轨道维持控制算法及分析

2.1 返回升交点的控制

(1)

当实际轨道与标称轨道存在偏差时，实际升交点经度也会偏离标称升交点，偏差dλ可表示为：

(2)

(3)

式中:Δλ为当前升交点经度偏差，Δλ0为初始升交点经度偏差。式(3)即为升交点经度偏差控制方程。飞船返回轨迹要求与标称轨迹重合，即要求Δλ=0，根据式(3)可解得，消除返回圈升交点经度偏差的轨道半长轴改变量Δac为：

(4)

式中:tr为返回时刻，tc为控制时刻。由Δac可得到消除升交点经度偏差的控制量Δvc。

从式(4)可以看出，轨迹控制量与时间历程相关，时间历程越长，Δvc越小，因此，从能量的角度来看，轨迹控制应尽早进行。很多文献[1-5]均分析了轨迹控制的特性，这里不再重复。

2.2 撤离点偏心率的控制及分析

撤离点偏心率的控制是和升交点控制相耦合的，为了在控制轨迹的同时兼顾控制轨道偏心率，将轨迹控制的Δvc分成两个脉冲执行。

(5)

如果控制点距飞船撤离点较近，则可以通过式(5)简单分配轨迹控制量Δvc来实现轨道偏心率控制。其中，Δv1为轨迹控制第一脉冲控制量，Δv2为轨迹控制第二脉冲控制量，k为分配系数。

如果控制点距离飞船撤离点很远，则必须要考虑摄动对轨道平均偏心率的影响。文献[15]给出了考虑地球J2和J3项时冻结轨道的必要条件，文献[7]给出了考虑地球J2和J3项时轨道平均偏心率的变化规律，说明轨道偏心率演化与初始轨道近地点幅角相关。图1给出了393 km高度近圆轨道，不同初始近地点幅角情况下，偏心率的中长期演化情况。地球引力场模型采用JGM-3模型32×32阶。

从图1可以看出，考虑地球更高阶非球形的情况下，目标近地点幅角选择90°附近时，轨道偏心率的演化较为平稳。所以在控制间隔时间较长的偏心率时，要对当前轨道偏心率和近地点幅角联合控制。

对于近圆轨道，引入偏心率矢量e=(ex,ey)：

(6)

式中:e为轨道偏心率大小，ω为近地点幅角。切向速度增量ΔvT对a和e的摄动方程可简化为：

(7)

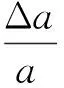
第一次脉冲控制位置u1=arctan(Δey/Δex)，控制量大小Δv1为：

(8)

第二次脉冲控制位置u2=u1+π(若第二次脉冲控制需与第一次脉冲控制间隔m圈，则u2=u1+(2m+1)π)，控制量大小Δv2为：

(9)

2.3 返回制动点高度与速度倾角的控制及分析

任务返回轨道参数制动点高度hbk和速度倾角sbk也需要双脉冲控制来实现。由式(8)和式(9)可知，求解双脉冲控制量需要确定目标轨道的半长轴a,偏心率e和近地点幅角ω，需要建立两组参数的函数关系。显然，由hbk和sbk无法唯一确定a,e,ω，所以引入优化变量，目标轨道返回制动时刻轨道真近点角f。

由椭圆轨道性质可得：

(10)

式中:μ为地球引力常数，p为轨道半通径，e为轨道偏心率，f为真近点角，s为真近点角为f时的速度倾角。由式(10)可知，在速度倾角s确定时，轨道偏心率e是真近点角f的单值函数。另有以下关系：

(11)

式中:r为制动点地心距，r0bk为制动点对应的地球半径，可以由轨道倾角和制动点星下点位置参数求得。联合式(10)和式(11)，可由f,hbk,sbk唯一确定a,e,ω，再由式(8)和式(9)求解飞船双脉冲控制量。由椭圆轨道性质可知，如果sbk>0，f的寻优范围为(0°,180°)，如果sbk<0，f的寻优范围为(180°,360°),令f在可优化范围内寻优则可得到不同约束的最优控制方案。

下面分析交会对接标称393 km高度近圆轨道在不同初始近地点幅角条件下，满足飞船返回制动点约束的飞船双脉冲维持特性。

图2～3中，f为目标轨道真近点角,u1表示第一脉冲控制点,ω0表示初始轨道近地点幅角,Δv表示飞船双脉冲控制的矢量和的大小。

从图2可以看出，由于目标速度倾角sbk为负，所以f在(0°,180°)范围内无解，随着f的变化，u1被分成两段，跳变点随ω0的不同而有所变化。如果以u1为自变量，从图3可以看出，在不同初始ω0的条件下，Δv随着u1的变化规律基本类似。随着u1的增大，Δv被分成了两段，在每段内均为单调递减，渐近线为u1=ubk-180°，记为u1j, Δv(u1=u1j-)=-∞, Δv(u1=u1j+)=+∞。

由以上特性分析可知，在不同初始轨道条件下，飞船返回双脉冲控制在满足返回制动点约束的同时，可以通过优化双脉冲控制的时机来控制Δv的大小，甚至是正负，以此来改变飞船撤离并执行返回维持后飞船、天宫以及伴星的三目标相对运动状态，从而规避三目标碰撞风险。

3 组合体与飞船联合轨道维持策略

由轨迹控制规律可知，消除升交点偏差的控制要尽早进行，所以第一次组合体维持安排在组合体形成后1天，考虑到控制执行误差以及组合体近30天的轨道预报误差，在飞船撤离前1～2天进行第2次维持来消除以上偏差，轨迹控制分为2个脉冲兼顾偏心率控制。飞船撤离执行固定撤离脉冲Δvspt，撤离后进行单体双脉冲控制，目标为飞船制动点轨道高度及速度倾角。由于组合体阶段轨迹控制与飞船返回制动点参数控制相互耦合影响，需要协同一体优化来实现4个目标参数满足要求。根据神舟十一号任务特点，采用第一次组合体与飞船联合规划时重点保证撤离点偏心率，第二次联合规划时重点保证撤离及返回阶段的相对飞行安全的策略。每次联合规划由组合体2个控制脉冲与飞船2个控制脉冲组成。因此，组合体轨道维持与撤离后飞船返回前轨道维持联合规划，设计变量包括：

ut1,Δvt1,ut2,Δvt2,us1,Δvs1,us2,Δvs2

目标量包括：

λret,espt,hbk,sbk

约束包括：

Rmin≥20 km，Rret≥100 km

其中，ut1,Δvt1,ut2,Δvt2是组合体双脉冲轨道维持的执行时刻和速度增量，us1,Δvs1,us2,Δvs2是飞船双脉冲轨道维持的执行时刻和速度增量，λret,espt,hbk,sbk分别是返回圈升交点经度、撤离时刻轨道偏心率、制动点高度和制动点速度倾角。

第一次组合体与飞船联合轨道维持策略迭代计算流程如下：

1) 初始条件设置。包括组合体初始轨道、组合体质量和大气阻尼面积、飞船单体质量和大气阻尼面积、摄动模型。

2) 利用初始轨道根据轨道模型外推积分，确定在初始轨道条件下控后偏心率演化平稳的目标轨道e,ω。

3) 初始轨道外推至返回圈升交点，计算初始偏差Δλ0。

4) 并通过轨迹控制方程式(4)确定Δa，从而得到目标轨道a。

5) 根据式(8)和式(9)求解组合体双脉冲控制位置和控制速度增量ut1,Δvt1,ut2,Δvt2。

6) 控后轨道外推至飞船撤离计算espt，施加撤离脉冲，转换飞船单体模型外推至返回制动点，计算高度hbk和速度倾角sbk。

7) 根据式(10)、式(11)确定目标轨道，根据式(8)、式(9)迭代计算飞船双脉冲控制位置和控制速度增量us1,Δvs1,us2,Δvs2。

8) 由于飞船控制影响了地面轨迹，飞船双脉冲控后轨道外推至返回圈升交点，重新计算升交点偏差Δλ。

9) 判断λret,espt,hbk,sbk是否均满足精度要求，如果不满足转至步骤4)；若满足，迭代计算结束。

第二次组合体与飞船联合轨道维持策略迭代计算流程基本相同，删掉步骤4)，步骤5)改为根据式(5)求解组合体双脉冲控制位置和控制速度增量ut1,Δvt1,ut2,Δvt2。在步骤7)后增加判断撤离至返回段3目标相对飞行轨迹步骤，如出现碰撞风险，返回7)优化双脉冲控制位置及速度增量直至能够规避碰撞风险。

4 组合体与飞船联合轨道维持控制算例

仿真计算中，组合体质量16200 kg，大气阻尼面积34.8 m2，飞船撤离后单体质量7800 kg，飞船单体大气阻尼面积24.7 m2。地球引力场模型采用JGM-3模型32×32阶，大气密度采用MSISE-90模型，阻尼系数Cd取2.2，地磁指数Ap取12，太阳辐射流量日均值F107和81天均值F107P均取120。

组合体第一次轨道维持安排在对接后1天，即飞船入轨后46圈和52圈执行组合体双脉冲控制，第二次轨道维持安排在飞船撤离前2天，即461圈和469圈。飞船在第489圈纳米比亚测控弧段内撤离，撤离脉冲为+0.5 m/s，飞船撤离后单体双脉冲轨道维持安排在第496圈，维持后飞船在505圈纳米比亚测控弧段内制动，506圈返回主着陆场。

4.1 第一次组合体与飞船联合轨道维持算例

第一次组合体与飞船联合轨道维持以优化撤离点轨道偏心率为主要目标。轨道维持前轨道瞬根数如表1所示，历元2016-10-29T02:23:00.00。

表1 第一次联合维持组合体初始轨道瞬根数Table 1 Complex’s orbit elements before the 1st united maintenance

表2给出了标称轨道以及轨道半长轴正负偏差5 km时，第一次飞船与组合体联合轨道维持规划结果。结果表明，通过第一次组合体与飞船联合轨道维持，撤离及返回的各个目标均能严格保证。

表2 第一次组合体和飞船联合轨道维持控制规划结果Table 2 Result of the 1st united maintenance

图4给出了标称初始轨道情况下，第一次组合体与飞船联合轨道维持后轨道平根数偏心率的演化情况。可以看出，利用组合体偏心率矢量双脉冲控制策略可以有效地控制控后轨道平根数偏心率的演化，使偏心率在撤离点时到达谷底。该策略还可以使控后轨道在组合体飞行30天内偏心率变化相对平稳，有利于科学实验的开展。

4.2 第二次组合体与飞船联合轨道维持算例

第二次组合体与飞船联合轨道维持以满足撤离和返回阶段3目标相对飞行安全约束为优化目标。

伴星在飞船撤离前6天结束科学实验，驻留在组合体后方一定距离处开始准备规避控制。Tspt- 6天组合体及伴星轨道分别如表3、表4所示，历元2016-11- 09T08:00:00.00。

表3 第二次联合维持组合体初始轨道瞬根数Table 3 Complex’s orbit elements before the 2nd united maintenance

表4 第二次联合维持伴星初始轨道瞬根数Table 4 Concomitant satellite’s orbit elements before the 2nd united maintenance

表5给出了第二次飞船与组合体联合轨道维持标称策略和优化策略的规划结果。

表5 第二次组合体和飞船联合轨道维持控制规划结果Table 5 Result of the 2nd united maintenance

在两种策略下，飞船撤离阶段相对天宫位置变化如图5～6所示。飞船撤离脉冲为+0.5 m/s，所以飞船撤离后相对天宫向后撤退，至飞船返回双脉冲维持执行时约在天宫后方50 km处，如果按标称策略实施飞船双脉冲控制，如图5所示，双脉冲速度增量和为负，飞船很快就会重新追赶上天宫，最小距离约20 m，存在很高的碰撞风险；如果结合规避控制对飞船双脉冲维持进行优化，如图6所示，同样满足飞船返回各项要求，但双脉冲速度增量和为正，飞船相对天宫继续向后撤退，与天宫相对距离逐渐增大，将不再存在与天宫的碰撞风险。根据优化结果，伴星与天宫也不存在碰撞风险，伴星仅需规避与飞船碰撞风险即可，在本算例中，伴星需要进行2次规避控制，均为降轨，每次速度增量为-0.37 m/s，至飞船返回时刻，伴星距飞船的距离约150 km。

5 结 论

本文研究了神舟十一号任务组合体与飞船轨道维持联合规划方法，建立了升交点经度、轨道偏心率、指定时刻轨道高度及速度倾角多目标特征参数的耦合控制方程；根据任务组合体及飞船的飞行特点及控制难点，提出了通过两次联合规划来满足不同约束的规划策略。在第一次组合体与飞船联合轨道维持策略规划时，通过对偏心率矢量的控制保证撤离点偏心率满足要求。在第二次组合体与飞船联合轨道维持策略规划时，提出了通过优化飞船双脉冲控制位置来控制双脉冲速度增量和的大小，甚至是正负，以此来改变飞船撤离并执行返回维持控制后飞船、天宫以及伴星的三目标相对运动状态，从而解决了规避三目标碰撞风险的关键一环，并通过算例验证了该方法的有效性。

本文继承并发展了文献[14]组合体与飞船联合轨道控制方法，在轨道长期偏心率控制和飞船返回双脉冲控制优化方面研究了新的方案，提出的组合体与飞船轨道维持策略联合规划方法在神舟十一号任务中得到了成功应用，保障了任务的高精度控制和返回阶段三目标的相对飞行安全，该方法也可用于后续空间站任务的轨道维持策略设计。