超大柔性空间结构姿态振动耦合稳定性分析

2018-08-10穆瑞楠谭述君吴志刚齐朝晖

宇航学报 2018年7期

穆瑞楠，谭述君,2，吴志刚,2，齐朝晖

(1. 大连理工大学工业装备结构分析国家重点实验室，大连 116024；2. 大连理工大学航空航天学院，大连 116024)

0 引言

以空间太阳能电站为代表，各类超大柔性空间结构概念相继出现[1-2]。这种结构的尺寸通常要达到千米量级，远超人类现有最大的空间结构——百米量级的国际空间站。随着结构尺寸的大幅增加，空间结构具有高柔性、质量分布高分散性、高面质比等特性。在环境干扰作用下，姿态运动和结构振动之间的耦合效应增强，有可能引发不稳定现象。因此，需要分析姿态运动与结构振动之间的耦合作用，以及系统参数对稳定性的影响。

在这一方面，已有学者以不同的简化模型开展了相关研究。以超大空间哑铃模型为简化研究对象，Sanyal等[3]推导了平衡位置处的线性化模型，分析了在两种平衡状态下的稳定性。穆瑞楠等[4]通过仿真分析，发现了结构振动引起的姿态运动不稳定现象。此外，以超大空间杆梁连续体模型为简化研究对象，Ashley[5]分析了不同姿态运动条件下的弹性杆结构振动稳定性问题，指出姿态运动对结构振动稳定性具有影响。Silva[6]给出考虑环境干扰的柔性梁平衡位置处非线性扰动方程，并用扰动分析方法讨论了系统可能出现的共振现象。Liu[7]考虑动力刚化效应，提出参数激励模型(PEM)，可更精确地描述在自旋姿态运动时的结构振动。Kumar 等[8]在小初始姿态角条件下，建立了3阶Hill方程形式的柔性梁振动方程，并发现对于模态频率与轨道角速率之比的平方较低时引起的不稳定现象。Shrivastava等[9]在Kumar等人的工作基础上，引入结构阻尼，并利用摄动方法考虑结构阻尼对结构振动稳定性的影响。魏乙等[10]在约束Hamilton体系下建立了绳系构型的轨道、姿态和结构振动的耦合模型，发现平台总体质量变化对其振动周期具有影响。Ishimura等[11]基于同一构型，分析了质量比、频率比以及长度比对系统稳定性的影响，仿真结果表明频率比影响最大，在某些参数范围内质量比影响较大。同时，Ishimura等[12]从势能角度提出评估系统稳定性的新方法，给出太阳能阵列平台在平衡位置附近的结构振动稳定性。McNally 等[13]基于算盘构型，分析了超大柔性空间结构在拉普拉斯轨道下的耦合动力学特性。Zhang等[14]建立了空间热辐射与结构振动的耦合模型，分析了在热辐射作用下的结构振动稳定性。Gettliffe[15]分析了带有电磁机构的绳系空间结构的运动稳定性。

本文在前期工作[4,16]的基础上，建立柔性梁在圆轨道下的姿态运动与弯曲振动的耦合动力学模型，分析姿态运动与重力梯度对模态频率的影响，并将柔性振动模态方程化为Mathieu方程形式，分析姿态运动幅度对柔性振动稳定性的影响。

1 在轨柔性梁的动力学建模

考虑细长的Euler-Bernoulli梁，建立超大柔性空间结构的动力学模型。假设空间结构在圆轨道运行，其姿态运动和弯曲变形均在轨道平面内，如图1所示，其中Oe表示地心，Re表示地球半径，rc表示空间结构质心处所在的轨道半径。

惯性坐标系和轨道坐标系分别用Oexeye和Ooxoyo表示，其坐标原点均位于地心。而浮动坐标系用Cxy表示，其坐标原点位于柔性梁的质心。梁上任一点P的坐标向量和变形向量分别用ρP和wP表示。基于质心浮动坐标系的定义，这两个向量满足以下三个条件：

(1)

(2)

(3)

rp=Teorc+TeoToa(ρP+wP)

(4)

其中Teo和Toa分别表示从轨道坐标系到惯性坐标系和从浮动坐标系到轨道坐标系的坐标转换矩阵。由此得到柔性梁的动能为

(5)

(6)

其中ms表示结构的总质量，I表示结构的转动惯量，其表达式为

柔性梁的重力势能可表示为

(7)

引入空间结构尺寸与轨道半径的尺寸比，重力势能的分母可展开成泰勒级数的形式为

(8)

其中ic表示轨道半径rc方向的单位向量。

基于Sincarsin[17]研究工作中的高阶惯性矩的递推定义，重力势能可近似表示为

(9)

其中特殊算子⊗表示并乘算子。将第一个简化条件式(1)代入式(9)，则重力势能可简化为

(10)

柔性梁的弹性势能可表示为

(11)

其中D材料的刚度系数矩阵，εE表示弹性应变。

对于在轨道平面内运动的柔性梁结构，可定义相应的向量和坐标转换矩阵。其中，在轨道坐标系内定义的轨道半径向量rc和轨道运动的角速度ωeo为

其中θ表示平面轨道角，而ωo表示轨道角速度。在浮动坐标系内定义的位置向量ρP、弯曲变形向量wP以及姿态运动的角速度ωoa分别为

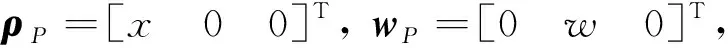
其中x表示柔性梁的轴向坐标，w表示柔性梁的横向变形，而φ表示平面姿态角。坐标转换矩阵为

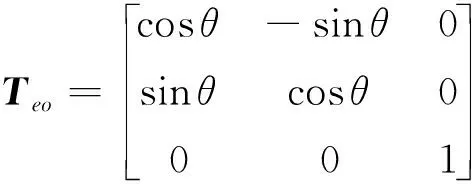
引入模态叠加法，弯曲变形可表示为

w(x,t)=φT(x)q(t)

(12)

其中φ(x)自由振动的弯曲模态函数列阵，q(t)表示模态坐标列阵。

以姿态角φ和模态坐标q(t)为广义坐标。利用Hamilton原理建立姿态运动和弯曲变形的耦合动力学模型，其中重力梯度项保留至尺寸比的二次项(参考式)。

qTR2q(15sin2φ-11)sinφ)=0

(13)

2R2q(5cos2φ-4)cosφ)=0

(14)

其中总质量ms、转动惯量I、模态质量矩阵Mq、模态刚度矩阵K、以及模态函数的积分列阵和矩阵可表示为

2 结构振动频率影响分析

通过简化结构振动方程式，弯曲振动的第一阶频率可以表示为

(15)

其中ωs表示结构弯曲振动基频。从式可以看出，结构振动频率受到系统转动和重力梯度两方面影响，等式右端第二项为转动耦合项，等式右端第三项为重力梯度项。在无主动控制的重力梯度稳定情况下，系统的姿态运动接近于简谐运动，由式可以看出，结构振动的频率会随姿态变化而波动。

将姿态运动近似表示为φ=φ0cosτ，其中φ0为初始姿态角，τ=kωot定义为广义时间，其中kωo为姿态运动频率。k与φ0的取值相关，通过近似的姿态运动响应与由耦合模型仿真得到的姿态运动响应相拟合，得到不同初始姿态角下的k取值，如图2(a)所示，而其拟合精度如图2(b)所示。由图可见在[ 0, 0.4π rad )范围内，拟合精度小于5%，因此这种近似是合理的。

(16)

图3给出式(16)中的转动耦合项和重力梯度项对结构振动频率随时间变化的影响曲线。对于小幅姿态运动情况(φ0= 0.1 rad)，对应的k=1.726，图3(a)中可见，在姿态运动幅度较小时，重力梯度作用使结构振动频率增加近似一倍轨道频率，但转动耦合项使结构振动频率降低约一倍轨道频率，二者影响近似相互抵消，此时结构振动频率变化幅度较小。对于大幅姿态运动(φ0= π/4 rad)，对应的k=1.469，从图3(b)可以看出，重力梯度项波动幅度增大至一倍轨道频率，时而使结构振动频率增大，时而使其减小。转动耦合项仍使结构振动频率降低，其量级增大至两倍轨道频率。

3 稳定性分析

通过对弯曲振动模态方程式(14)的合理简化，可化为Mathieu方程形式。忽略式中重力梯度的尺寸比二次项，则第n阶的模态方程为

(17)

不失一般性的假设姿态运动为φ=φ0sinτ，其中τ=kωot+π/2。同时，引入简化变量

将假设的姿态角φ的表达式代入模态方程式(17)，并用τ的微分式替换t的微分式，同时代入简化变量ε和δn，则模态方程式(17)化为

(18)

从(18)式可见，模态方程由此化为高阶Mathieu方程，其中ε为小参数。基于稳定性的摄动分析方法，令模态坐标qn和参数δn为

qn=qn 0+εqn 1+ε2qn 2

(19)

(20)

将模态坐标qn和参数δn的表达式代入Mathieu方程式(18)，比较小参数ε同幂次顶系数,得

(21)

(22)

(23)

由小参数ε的零次幂方程式解得

qn 0=a0cos(δn 0τ)+b0sin(δn 0τ)

(24)

其中a0和b0为待定常数，由弯曲变形的初始条件决定。由于Mathieu方程的特点，在式(18)的小参数一次项的余弦函数中，广义时间的系数为1，因此参数δn 0=1/2及其附近为主要共振区域。将式(24)及参数δn 0代入小参数ε的一次幂方程式(22)。为了消除一次幂方程中的永年项，出现两种情况，分别为

(25)

(26)

qn 0=a0cos(0.5τ)

将qn 0和qn 1的表达式代入小参数ε的二次幂方程，并为了消除二次幂方程中的永年项，可得

(27)

解得

(28)

由式(25)和式(27)可得，第一种情况下的参数δn表达式为

(29)

(30)

由式(29)和式(30)，得到不同初始姿态角下的稳定区域如图4所示。由图2(a)可知，随着初始姿态角增大，姿态运动频率与轨道角速度之比k减小，而不稳定区域增大。