配电网区间线性三相潮流的非迭代仿射求逆计算方法

敖 鑫, 王 淳

(南昌大学电气与自动化系， 江西省南昌市 330031)

0 引言

随着可再生能源大规模并网，新能源出力的间歇性和用电侧负荷的不确定性对电网的影响日趋显著，加剧了潮流分析的复杂程度。基于单一断面的潮流计算方法缺乏对系统不确定因素的考虑，无法为电力系统的静态安全分析提供充分的依据，需要开展计及不确定性的潮流计算。区间潮流计算利用区间数描述不确定信息，根据变量的边界信息计算潮流的可能分布范围，具有建模简单、所需信息少的优点[1-2]。

为处理系统中存在的区间不确定性，文献[3]将区间分析法用于直流潮流计算中，将区间潮流计算问题转化为求解常系数的区间线性方程组问题，并采用区间高斯消元法对其进行求解。文献[4-5]建立了配电网元件的区间模型，将区间分析法应用到前推回代算法中。但区间数存在不能描述变量间相关性的固有缺陷[6]，直接采用区间四则运算进行高斯消元或者前推回代易使计算结果过于保守。为降低区间潮流计算的保守性，文献[7]研究了更改区间数表示方式对解集保守性的影响；文献[8]和文献[9]分别采用Krawczky算法和带预处理的区间Hull算法求解区间直流潮流方程，提升了区间直流潮流的计算精度；文献[10]在极坐标牛顿法的基础上，采用Krawczyk-Moore算子进行区间迭代并求解区间潮流，在算子的计算中引入了仿射运算，有效降低了潮流解的保守性；文献[11]将含二次约束的二次规划模型进行线性松弛后，再应用于求解输电网区间潮流问题，通过最优边界紧缩方法收缩解集外壳，提高了计算精度，但与仿射方法相比需要消耗更多的计算时间；文献[12-15]采用仿射数描述区间变量间的相关性，利用仿射四则运算进行不动点潮流迭代，有效降低了配电网区间潮流计算的保守性，但需要进行反复的迭代以获取收敛的潮流解，当系统负荷较重或者负荷的区间变动范围较大时，会导致计算量增加甚至不收敛。文献[16]在仿射快速分解法潮流的每步迭代中引入线性优化方法，抑制了区间的增长，但不适用于高电阻/电抗(R/X)比值的配电网。文献[17]利用变量的仿射展开，将区间潮流计算问题转换成了求解线性规划、非线性规划和二次规划等3个优化问题，提出了适用于输电网的非迭代区间潮流算法，但构造优化模型时利用了直流潮流模型，无法直接拓展应用到配电网计算中。

基于上述原因，本文以线性三相潮流方程为基础，采用仿射数描述区间变量，将配电网区间潮流计算转换为求解仿射线性潮流方程组，并尝试引入一种非迭代的仿射矩阵求逆方法对其进行求解，通过仿射求逆运算以及对仿射方程的保守估计推导出仿射节点电压的显式计算公式，从而避免了区间潮流计算的迭代过程。最后采用多个三相不平衡系统作为算例，对所提方法的计算性能进行了验证与比较。

1 仿射矩阵及其求逆方法

区间数学将不确定变量采用区间数表示，但区间数无法描述变量间的关联关系，在计算过程中易导致区间扩张。仿射数学将不确定变量用一组仿射线性多项式表示，可以描述区间变量之间的联系，从而可以有效降低区间运算的扩张性。区间数和实仿射数的定义以及四则运算公式[18]详见附录A。

1.1 仿射矩阵

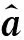
(1)

(2)

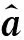
1.2 仿射矩阵的逆运算

为减轻区间运算带来的保守性问题，在2010年D.Degrauwe提出了一种求解仿射系统的线性方程组的解法[19]，并以3个结构分析中的实际问题为例，验证了方法的有效性。求解仿射线性方程组的核心就是对仿射矩阵进行求逆，以下介绍仿射矩阵求逆的主要原理。

根据Neumann级数，矩阵的逆可展开为：

(E+X)-1=E-X+X2-X3+…

(3)

式中：E为单位矩阵；X为任一方阵，其谱半径ρ(X)小于1，这一条件在一般应用领域内均能满足[19]。

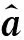
(4)

(5)

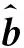
(6)

若保留式(6)中噪声元的一次部分，be∘εem作为其余高次部分的保守估计值，则b0和bi的计算公式分别如式(7)和式(8)所示，be保守估计的计算公式如式(9)所示，对应的方法称为一次展开法。若保留式(6)中噪声元的二次部分，be∘εem作为二次以上噪声元的保守估计值，则b0的计算公式变为式(10)，be的计算公式变为式(11)，bi的计算公式仍为式(8)，对应的方法称为二次展开法。一次展开法与二次展开法的详细推导过程可参考附录B。

b0=E

(7)

bi=-aii=1,2,…,m

(8)

be=Z2(E-Z)-1

(9)

(10)

Z3(E-Z)-1

(11)

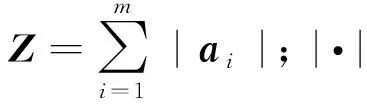
2 基于仿射求逆的区间线性三相潮流计算方法

2.1 线性三相潮流算法

(12)

式中：IN为非平衡节点的注入电流构成的向量，可根据电阻/电流/功率(ZIP)负荷模型计算得到；YNN为其余节点的导纳矩阵；YNS为平衡节点与其余节点之间的互导纳矩阵。

在IEEE标准算例[20]中，ZIP负荷模型的恒电流分量和恒阻抗分量均为折算到标称电压Vnom=1.0(标幺值)下的复功率，其负荷的单相ZIP组合模型如式(13)所示。

(13)

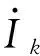
负荷模型中，恒注入功率部分是非线性的，要得到最终的节点电压需要进行高斯迭代，这种迭代方法就是隐式Zbus高斯法[21]。在配电网中，其余节点与平衡节点之间的相角差实际上很少超过±10°[22]。根据配电网的这一特点，可对负荷模型中的非线性部分作线性近似，推广到三相模型后如式(14)所示。

(14)

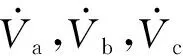
根据线性简化方法，最终的配电网潮流方程简化为式(15)所示的一组复线性方程组,整理成实线性方程组如式(16)所示，式(15)和式(16)出现的新矩阵计算公式详见附录C的式(C1)至式(C4)，潮流方程线性化的详细推导过程可参考文献[23]。

(15)

DVr-m=-Ar-m

(16)

式中：A,B,C为系数矩阵；D为实系数矩阵；Vr-m和Ar-m分别为由VN和A矩阵元素的实部和虚部构成的实矩阵。

2.2 区间线性三相潮流的仿射求逆计算原理

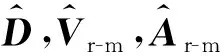
(17)

为便于区分，记三相模型中同一处不同相的多个节点为一个端点。线路阻抗参数的不确定性很小，可视为确定值，各个节点的负荷均视为区间值，其中恒功率负荷的有功分量和无功分量采用仿射数表示后分别如式(18)和式(19)所示，恒电流和恒阻抗负荷的仿射表示类似，不再赘述。

(18)

(19)

式中：SP,re,i和SP,im,i分别为节点i的恒功率分量中有功功率和无功功率的中值；ΔSP,re,i和ΔSP,im,i分别为节点i恒功率分量中的有功功率和无功功率的不确定分量。

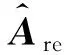
(20)

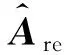
各项噪声系数矩阵的计算式详见附录C式(C8)至式(C13)。仿射矩阵的求逆要求中心值为单位矩阵，因此须对式(17)进行单位化处理，如式(21)所示。

(21)

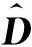
将式(21)简写为式(22)，从而得到仿射节点电压的计算式(23)。

(22)

(23)

(24)

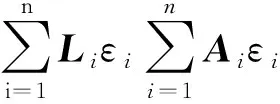
(25)

(Le∘εem)A0⊆(|Le||A0|)∘εev2

(26)

(27)

式(25)至式(27)右侧保守估计的噪声元对应的系数矩阵均为正，故满足式(28)，从而得到仿射逆阵与仿射向量的乘积可用式(29)表示。根据式(29)可直接计算得到仿射节点电压。

(28)

式中：εev为n维噪声元向量。

(29)

3 算例分析

3.1 计算精度比较

以IEEE 37节点系统[25]作为算例，移除调压器，并假定节点的各相负荷具有恒定功率因数，负荷大小均在确定数值的±10%范围内波动。采用以下4种区间潮流计算方法对算例进行计算与比较。

方法1：基于蒙特卡洛模拟的隐式Zbus高斯法，对负荷数据在不确定范围内进行随机抽样，利用隐式Zbus高斯法进行潮流计算并统计得到潮流上、下界，随机抽样次数设置为104。该计算方法未经过线性化处理，得出的是精确潮流解，在后续比较中将以该方法计算得到的区间作为参考标准。

方法2：基于区间迭代的Krawczyk算法，采用区间算法进行区间迭代并求解式(16)构成的区间线性潮流方程组。

方法3： 在方法2的基础上，采用仿射方法[10]计算Krawczyk算子，并迭代求解区间线性潮流方程组。

方法4：基于仿射求逆的区间线性三相潮流算法，利用本文所述仿射矩阵求逆方法中的一次展开法求解仿射线性潮流方程组。

方法1至方法3的收敛精度均设为10-5。系统中A相节点电压的实部和虚部区间分别如图1和图2所示。在图1和图2中，方法2的区间范围很大，存在严重的保守性问题，原因是区间数不能描述区间变量的相关性，采用Krawczyk算法进行区间迭代易使结果产生较大误差。方法3在计算Krawczyk算子中采用了仿射运算，得到的解集外壳区间要比方法2窄，但在每次迭代中，计算得到的仿射数需要转换为区间数后与前一次迭代的结果进行区间交集运算才能得到新的迭代算子，仿射数转区间数的过程中会使仿射信息出现无法避免的丢失，从而无法充分利用仿射运算的优势。方法4通过直接求解仿射线性方程组，能够充分利用所有的仿射信息，与方法2和3相比，其区间外壳最为贴近方法1，且完全包含了方法1的计算结果，说明方法4兼具完备性和低保守性。

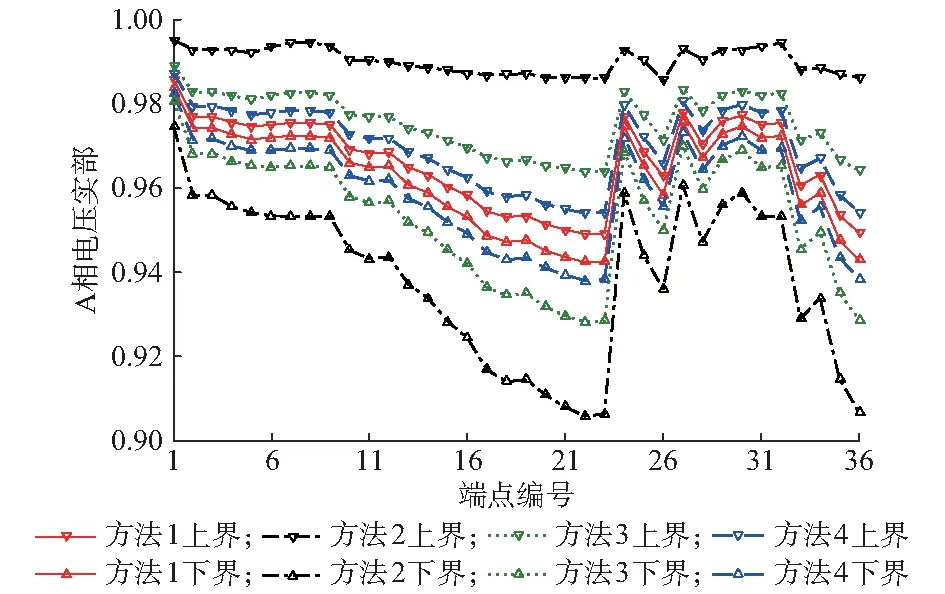
图1 A相节点电压实部区间Fig.1 Real part of nodal voltage bounds of phase A

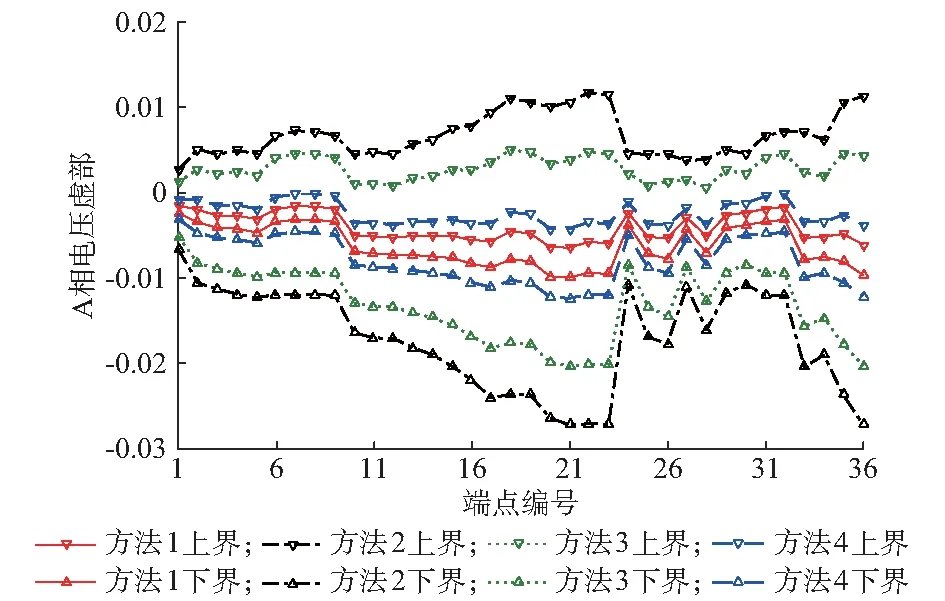
图2 A相节点电压虚部区间Fig.2 Imaginary part of nodal voltage bounds of phase A

3.2 一次展开法与二次展开法的比较

(30)

(31)

当计算值具有保守性时，μ+/μ-均大于0，且它们的值越小表示离标准结果越近。基于一次展开法和二次展开法计算得到的部分端点的电压A相实部的偏差如表1所示。表1中，二次展开法的各端点的上、下偏差均不超过一次展开法，表明二次展开法的结果更逼近标准结果，但它与一次展开法计算结果的偏差率不足0.1%，在工程上可以认为是等同的，考虑到一次展开法计算量更小，因此在配电网计算中，一次展开法完全可以满足需要。

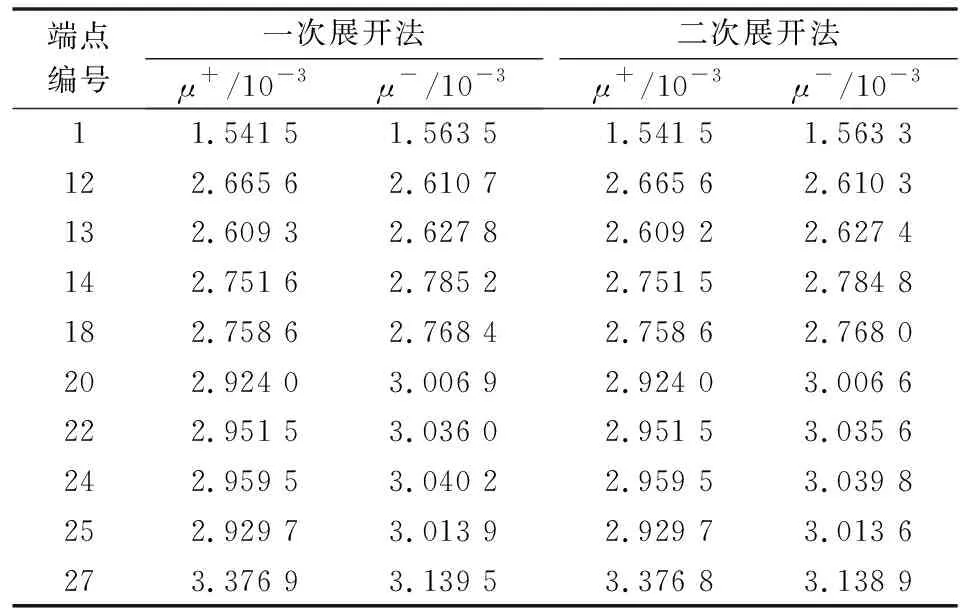
表1 一次展开法与二次展开法的偏差Table 1 Errors of firsts order expansion method and second order expansion method

3.3 不确定度下的性能测试

为测试算法在不同不确定度下的计算性能，将不确定范围从±10%增加到±50%，分析方法2至方法4的计算性能。附录D图D1为3种方法在多个不确定度下的偏差分布，其中图D1(a)各相的最小偏差和图D1(b)最大偏差分别指的是在所有端点中，该相的上、下偏差的最小值和最大值，它们分别表示区间外壳的最窄部分和最宽部分，可以体现算法的保守性和完备性。图D1(a)中，采用3种方法得到的各相最小偏差均大于0，说明3种方法在多个不确定度下得到的结果均是完备的；随着不确定度的增加，最大偏差和最小偏差都呈现近似线性增加的趋势，偏差曲线的斜率为方法2>方法3>方法4，说明随着不确定度的增加，方法3的误差增速要小于方法2，方法4的误差增速最小，更适用于具有较高不确定性的场合。

附录D图D2给出了多个不确定度下3种方法的迭代次数分布。方法4无须多次迭代，因此迭代次数恒定为1。方法2和方法3在多个不确定度下都能得到收敛解，随着不确定度增加，方法2和方法3的迭代次数呈现不变或增加的趋势，其中方法3的迭代次数增长速度明显比方法2慢，表明仿射运算的引入能够有效改善区间潮流算法的收敛性能。

3.4 计算速度的比较

采用IEEE 13节点系统[25]、IEEE 33节点系统[26]、IEEE 37节点系统[25]和IEEE 123节点系统[25]4个三相不平衡系统作为算例，比较4种区间潮流算法的计算时间，如表2所示。在小型系统计算中，方法3的迭代次数大多比方法2少，在计算速度上具有微弱的优势，在大型系统中(IEEE 123节点系统)，虽然方法3的迭代次数更少，但总体计算时间仍更多，这与仿射法的噪声元数量增多有关；在所有算例中，方法4均具有最高的计算效率，这是因为方法4只须进行一次仿射计算即可得到最终解，避免了迭代过程中花费的时间，即使在大型系统的计算中，仍具有很高的计算效率。类似地，当系统状态变差时，方法4能够有效避免效率下降的问题，以IEEE 37节点系统为例，将负荷大小从初始负荷的1倍增加至7倍，负荷的不确定度恒定为±10%，定义计算时间比为算法在当前负荷水平下的计算时间和初始负荷水平下的计算时间的比值，四种区间潮流计算方法在不同负荷比重下的计算时间比如附录D图D3所示。附录D图D3中，方法1至方法3的计算时间比随着负荷比重的增加呈现上升趋势，而方法4的计算时间比基本保持恒定，计算效率最为稳定。

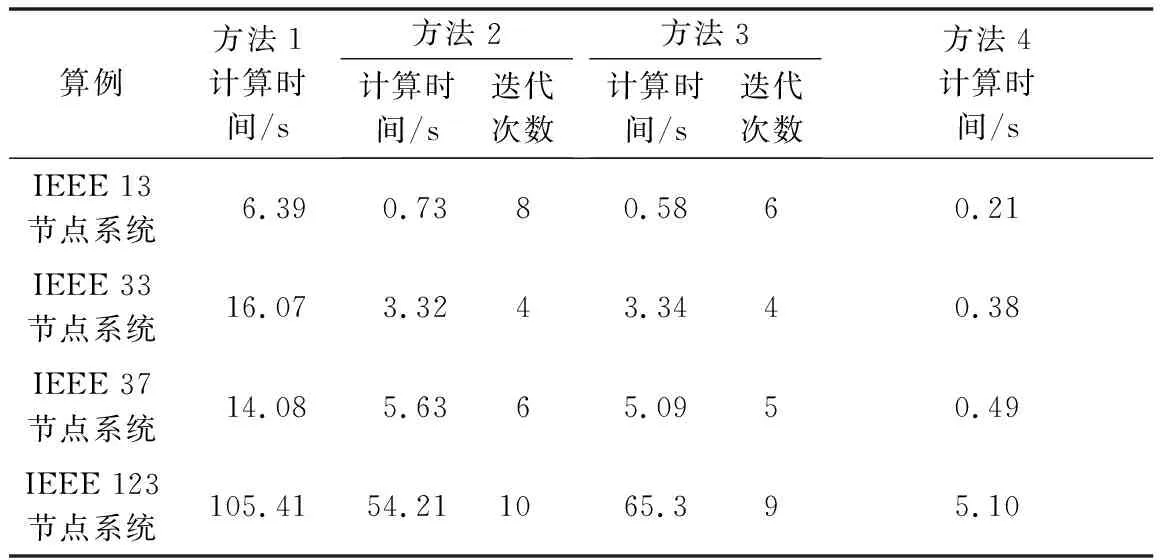
表2 计算时间比较 Table 2 Comparison of computing time

4 结语

将仿射矩阵求逆方法和线性三相潮流算法相结合，提出了配电网区间线性三相潮流的非迭代仿射求逆计算方法。采用仿射数描述区间变量间的关联关系，将潮流方程组转化为仿射线性方程组，降低了区间运算的保守性,利用仿射矩阵的求逆方法求解仿射线性方程组。算例分析采用基于蒙特卡洛模拟的隐式Zbus高斯法作为参考标准，对比研究了本文算法的计算性能，结果表明：①仿射矩阵求逆方法适用于求解配电网的区间潮流计算问题，其中二次展开法比一次展开法能获得更为紧凑的区间外壳，但两者相差极小，在潮流计算中，一次展开法即可满足工程需要；②基于仿射求逆的配电网区间线性三相潮流算法无须迭代，不存在收敛性问题，具有较快的计算速度和稳定的计算效率。

本文研究未涉及讨论如何处理配电系统中的其余非ZIP负荷类型的元件。当系统中存在多种节点类型的分布式电源或考虑调压器的调压作用时，区间潮流计算都将变得更加复杂，这些都是未来需要进一步考虑和完善的地方。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。