计及可再生能源不确定性的孤岛微电网概率潮流计算
2018-08-09徐潇源唐俊刺周纯莹
王 晗, 严 正, 徐潇源, 李 铁, 唐俊刺, 周纯莹
(1. 电力传输与功率变换控制教育部重点实验室(上海交通大学), 上海市200240;2. 国网辽宁省电力有限公司, 辽宁省沈阳市 110004)
0 引言
随着全球能源危机和环境污染问题日益突出,大力发展风电、太阳能发电等可再生能源,是中国乃至全球能源与经济实现可持续发展的重大举措[1-2]。目前,微电网以分布式电源(distributed generation,DG)的形式高效集成各种可再生能源,有利于促进多能源之间的综合利用,提高可再生能源的渗透率,降低对环境的污染[3-5]。而随着未来可再生能源接入微电网的比例不断提高,具有不确定性的风电、光伏等能源将使微电网的安全稳定运行受到挑战。因此,计及可再生能源的不确定性,研究系统不确定性因素对微电网安全稳定运行的影响具有重要意义。
微电网有并网运行和孤岛运行两种运行方式,在孤岛运行方式下,微电网的控制策略主要有主从、对等和综合控制[6]。其中,对等控制和综合控制下,系统内不含平衡节点,孤岛微电网的频率和电压稳定需要具有下垂控制的DG装置维持,这使得DG的不确定性对系统频率和电压的影响更为突出。近年来,已有相关文献建立了孤岛微电网的潮流计算模型,进而分析了系统频率和电压的稳定性。文献[7]将孤岛交流微电网中的DG装置处理为松弛PQ节点,采用改进的潮流计算方法进行潮流计算。文献[8]把DG装置处理为PQ节点、PV节点和下垂控制节点,建立了分散下垂控制策略下孤岛交流微电网的潮流计算模型,并采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)信赖域算法进行求解。文献[9]考虑了孤岛交流微电网的下垂控制策略,建立了孤岛交流微电网的三相潮流计算模型,并利用牛顿信赖域算法进行潮流计算。上述文献为孤岛交流微电网的潮流计算提供了基础,但均没有计及可再生能源的不确定性,不能体现具有随机特性的风电、光伏发电对孤岛微电网运行稳定性的影响。
同时,目前孤岛微电网潮流计算的文献[7-10]中,下垂控制策略均采用有功功率—频率/无功功率—电压(P-f/Q-U)控制,此时需要逆变器型DG出口处等效阻抗呈感性,而由于微电网内线路阻感比较大,在某些情况下等效阻抗会呈现阻性,此时需要采用有功功率—电压/无功功率—频率(P-U/Q-f)的下垂控制策略[11-12]。所以,计及DG的不确定性并考虑上述两种不同的下垂控制策略时,需要采用鲁棒性强、收敛速度快的算法进行潮流求解。相比于目前孤岛微电网潮流计算常用的牛顿法、信赖域算法,自适应Levenberg-Marquardt(LM)算法[13]的收敛性强,并且近年来高阶LM算法[14-15]的提出为其进一步应用奠定了基础。
本文计及可再生能源的不确定性,基于P-f/Q-U和P-U/Q-f两种下垂控制策略,建立了综合控制下孤岛微电网的概率潮流计算模型,并提出了一种改进的三步Levenberg-Marquardt(MTLM)算法对潮流方程进行求解。采用基于Sobol序列的拟蒙特卡洛(quasi-Monte Carlo,QMC)模拟获得具有随机性的DG和负荷的样本,进而对38节点孤岛交流微电网进行概率潮流计算,通过对比验证了MTLM算法的快速收敛性和鲁棒性,研究了不同下垂控制策略下系统频率和电压的概率分布情况,分析了具有随机性的高比例可再生能源接入对孤岛微电网的影响。
1 孤岛交流微电网概率潮流计算模型
1.1 不同下垂控制策略的节点建模
在综合控制的孤岛运行模式下,交流微电网内的DG装置可处理为PQ节点、PV节点及下垂控制节点[8],系统内不存在平衡节点,主要依靠下垂控制节点来实现频率和电压的控制。根据逆变器型DG出口处等效阻抗呈现阻性或感性,目前主要有P-U/Q-f和P-f/Q-U两种下垂控制策略。一般交流微电网的配电线路阻感比较大,等效阻抗呈阻性,此时DG接口逆变器采用P-U/Q-f下垂控制策略[16];而在某些情况下,滤波电路、变压器等感性原件的引入及虚拟阻抗[17]方法的应用,使得等效线路的阻感比变小,等效阻抗呈感性,此时P-f/Q-U下垂控制策略能更好地实现电压、频率控制及功率分配。本文考虑上述两种不同的下垂控制策略,对下垂控制节点进行建模。
1)P-U/Q-f下垂控制节点
P-U/Q-f下垂控制策略的下垂特性曲线如附录A图A1所示,根据P-U/Q-f的下垂特性,可得下垂控制节点的潮流计算模型为:

(1)
式中:m1pi和n1qi分别为P-U/Q-f下垂控制有功、无功功率的静态下垂增益;P1Gi和Q1Gi分别为P-U/Q-f下垂控制节点i流入交流微电网的有功、无功功率;U1i和ω1分别为P-U/Q-f下垂控制节点i的空载输出电压幅值和空载角频率;Ui为节点i的实际输出电压幅值;ω为交流微电网的稳态角频率。
2)P-f/Q-U下垂控制节点
P-f/Q-U下垂控制策略的下垂特性曲线如附录A图A2所示,根据P-f/Q-U的下垂特性,可得下垂控制节点的潮流计算模型为:
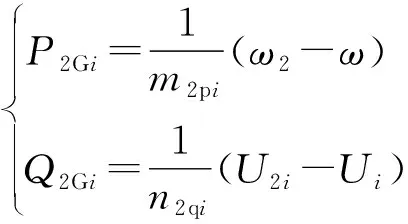
(2)
式中:m2pi和n2qi分别为P-f/Q-U下垂控制有功、无功功率的静态下垂增益;P2Gi和Q2Gi分别为P-f/Q-U下垂控制节点i流入交流微电网的有功、无功功率;U2i和ω2分别为P-f/Q-U下垂控制节点i的空载输出电压幅值和空载角频率。
1.2 负荷模型
一般潮流计算中,负荷模型通常为工频下的静态负荷模型,而在综合控制孤岛运行模式下,交流微电网的频率一般不会稳定在工频,因此静态负荷模型需考虑负荷点端电压和频率的影响[18]。
(3)
式中:ω3为交流微电网的设定角频率;PLi和QLi分别为负荷节点i实际的有功、无功功率;P0i和Q0i分别为负荷节点i在设定频率下的有功、无功功率;Ui为负荷节点i实际电压的幅值;α和β分别为负荷有功、无功功率指数,不同类型的负荷指数值不同;hpf,i和hqf,i为负荷节点i的静态频率特性参数。
1.3 节点功率方程
在综合控制孤岛运行模式下,对交流微电网内的PQ节点、PV节点及下垂控制节点建立功率平衡方程,PQ节点的功率方程为:

(4)
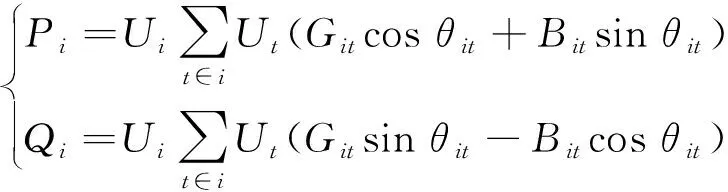
(5)
PV节点的功率方程为:
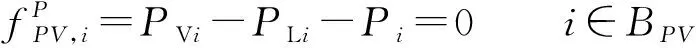
(6)
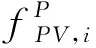
不同控制策略下的下垂控制节点的功率方程为:
(7)
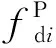
综合PQ节点、PV节点及下垂控制节点的功率平衡方程,其中,下垂控制节点无论采用P-U/Q-f下垂控制策略,还是P-f/Q-U下垂控制策略,在综合控制孤岛运行模式下,交流微电网的节点功率方程均为一组非线性方程,其紧凑形式可表示为:
F(x)=0x∈Rn
(8)
式中:x为待求变量;n为待求变量总数。
设孤岛交流微电网总的节点数为M,其中包括MPQ个PQ节点、MPV个PV节点、以及MD个下垂控制节点,则系统的待求变量数和方程数见表1。

表1 系统的变量数和方程数Table 1 Numbers of variables and equations
一般节点1的相角θ1设为0(标幺值),待求变量加入系统频率ω,则系统的待求变量总数为n=2M-MPV,待求变量可表示为:
x=[ωθ1…θMU1…UMPQUMPQ+1…UMPQ+MD]
(9)
在孤岛交流微电网中,PV节点和下垂控制节点的输出功率达到限制值时,会转化为PQ节点。同时,由线路参数的频率响应特性[10]可知,在交流微电网稳态运行的频率范围内,频率偏差对线路参数的影响很小,因此,本文节点功率方程中保持线路参数不变。
由于风速和光照强度的随机性,DG的出力也具有不确定性。本文计及可再生能源出力的不确定性、负荷有功、无功功率的波动性,待求变量x及线路的传输功率均具有概率特征,因此,式(8)为计及孤岛微电网内不确定性的概率潮流计算模型。
2 MTLM算法
孤岛微电网潮流计算实质为求解一组非线性方程,常用的方法包括牛顿法、信赖域算法、LM算法等。其中,牛顿法对初值的依赖性高,孤岛微电网中不存在平衡节点,且待求变量包含系统频率,初值的选取不当会导致牛顿法发散,并且在迭代过程中雅可比矩阵奇异时,牛顿法无法求解;信赖域算法具有全局收敛性,对初值的敏感性低,但其仅在部分情况下二阶收敛,在求解计及不确定性的概率潮流方程时会降低计算效率;传统单步自适应LM算法对初值的依赖性低,可保证迭代过程中雅可比矩阵非奇异,但不具有全局收敛性,每次迭代时雅可比矩阵需要重新计算,不利于提高孤岛微电网概率潮流的计算效率[13]。
因此,针对不同下垂控制策略下的孤岛微电网概率潮流计算模型,本文在传统单步自适应LM算法的基础上,并结合线搜索技术,提出了用于求解上述模型的MTLM算法。该算法对初值的敏感性低,鲁棒性强,提高了雅可比矩阵在迭代过程中的利用率,具有全局收敛性,且在满足部分条件下具有4阶收敛速度,有利于提高孤岛微电网概率潮流的计算效率。其中,MTLM算法收敛特性的进一步阐释可见本节末。
基于MTLM算法求解式(8)的步骤如下。
步骤1:设置迭代初值x1∈Rn,初始迭代次数k=1,最大迭代次数为N,收敛精度为ε,初始自适应因子μ1>m>0,m为自适应因子的下限值。

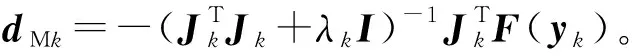
步骤5:令zk=yk+αkdMk,其中αk为引入线搜索技术后所得的步长,可由下述子问题求得。即

(10)
式中:αM为步长αk的上限值,且αM>1。
上述子问题可展开为αk的二次函数,进一步得到线搜索步长αk的表达式为:
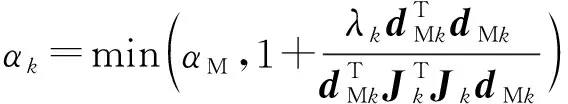
(11)
步骤7:得到当前总迭代步dk=dLk+αkdMk+dHk。
步骤8:计算总迭代步的取舍指标rk。即
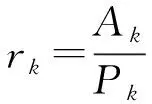
(12)
Ak=‖Fk‖2-‖F(xk+dLk+αkdMk+dHk)‖2
(13)
Pk=‖Fk‖2-‖Fk+JkdLk‖2+
‖F(yk)‖2-‖F(yk)+αkJkdMk‖2+
‖F(zk)‖2-‖F(zk)+JkdHk‖2
(14)
式中:Ak和Pk分别为F(x)在迭代点xk的实际下降量和预测下降量。
步骤9:根据取舍指标rk的值,判断是否接受迭代步。即
(15)
式中:c0为接受当前总迭代步的判别系数。
步骤10:更新自适应因子μk。即
(16)
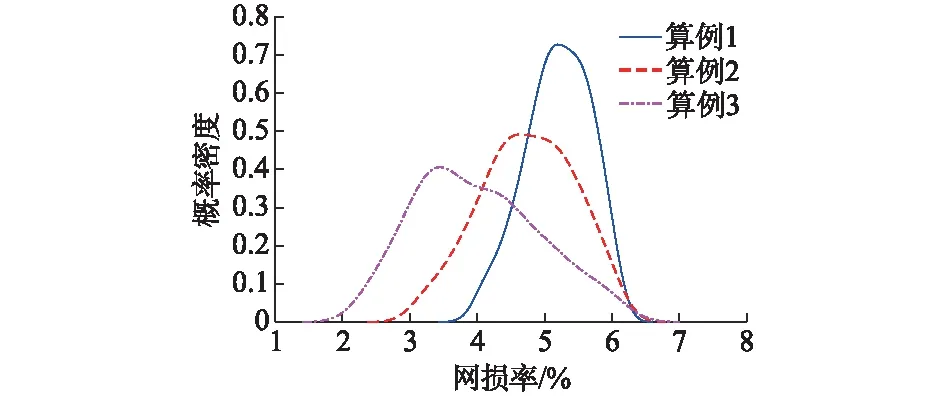
式中:c1和c2分别为自适应因子更新的判别系数,且0 步骤11:k=k+1,转步骤2,继续迭代计算。 如上所述,其中步骤3至步骤7中MTLM算法多次利用了雅可比矩阵,并且结合线搜索技术,对迭代步进行调整,这是相对于传统单步自适应LM算法的主要改进。进一步,MTLM算法中自适应因子的调整,能够使得迭代过程避开奇异区域,有效避免因雅可比矩阵奇异导致的潮流发散,保证潮流的收敛性。同时,三次迭代步的计算提高了雅可比矩阵的利用率,降低了计算的复杂性。并且,线搜索技术的引入进一步加快了收敛速度,MTLM算法有如下收敛特性[15]。 1)当F(x)连续可微,且F(x)和J(x)为Lipschitz连续时,MTLM算法具有全局收敛性。 2)当F(x)连续可微,且J(x)在x*的邻域N(x*,b)内Lipschitz连续,其中b∈[0,1),同时‖F(x)‖在N(x*,b)内有局部误差界时,MTLM算法具有4阶收敛速度。 由于地理位置、气象环境等因素的共同作用,一个地区内的风速之间及光照强度之间均具有一定的非线性相关性,使得微电网中相同类型的DG出力之间也是相关的。本文通过拟合优度检验方法,构建合适的Copula函数[19]来描述风速或光照强度之间的非线性相关性,进而获得风速或光照强度的联合分布;对于独立的DG,采用非参数核密度估计[20](kernel density estimation,KDE)得到风速或光照强度的累积分布函数(cumulative distribution function,CDF)。获得风速或光照强度的概率分布后,采用基于Sobol序列的QMC模拟[21]进行采样,并根据文献[22]中风电和光伏有功功率的计算公式,获得DG有功出力的样本。其中,风电机组采用恒定功率因数控制;光伏电池向微电网注入有功功率的同时,可进行无功补偿。 孤岛交流微电网内的负荷包括居民负荷、工业负荷、商业负荷,相同类型负荷之间的波动量也存在相关性。本文采用相关系数矩阵描述负荷随机波动量之间的相关性,并以期望为0,标准差为各节点基准负荷百分数的正态变量表示负荷的随机波动量。实际节点负荷为基准负荷与负荷随机波动量之和,其中保证负荷节点的功率因数不变。 根据上述得到的风速、光照强度及负荷的概率分布,本文采用基于Sobol序列的QMC模拟获得输入随机变量的样本,进而通过MTLM算法实现孤岛微电网的概率潮流计算,最终获得输出变量的统计特征,其计算流程如附录A图A3所示。 根据文献[9]在IEEE 33节点系统的8,12,22,25,29节点分别接入5个DG装置,包括2个风电机组、1个光伏电池及2个燃气轮机,构成38节点孤岛交流微电网系统,如附录B图B1所示。DG装置接入系统的线路参数可见附录B的表B1,其中,风电机组所在的34,35节点处理为PQ节点,光伏电池所在的36节点处理为PV节点,风电机组和光伏电池的数据如附录B的表B2和表B3所示;燃气轮机所在的37,38节点为下垂控制节点,可采用P-U/Q-f或P-f/Q-U下垂控制策略,下垂控制参数如附录B表B4所示。其中,P-U/Q-f和P-f/Q-U下垂控制策略的空载角频率和空载输出电压幅值的标幺值分别为ω1=0.996,U1i=1.06和ω2=1.004,U2i=1.06。系统的基准容量为1 MVA,基准频率为50 Hz,孤岛交流微电网正常运行时系统的稳态频率范围为50±0.2 Hz,其总负荷在设定角频率ω3=1.000(标幺值)时为3.715+j2.3(标幺值)。 在配置为Corei5 3.0 GHz CPU,8 GB内存的计算机上,利用MATLAB编制潮流计算程序。改进信赖域算法参数可见文献[23],传统单步自适应LM算法参数可见文献[13]。本文所提MTLM算法的参数设置为:N=40,ε=10-6,μ1=0.1,m=0.001,δ=1,αM=20,c0=0.000 1,c1=0.25,c2=0.75,η1=4,η2=0.25。 根据2个风电场风速的历史数据,采用Copula函数构建具有非线性相关性的风速的联合分布函数,并通过拟合优度检验中的Kolmogorov-Smirnov(K-S)检验法和Q-Q图检验法,确定选取拟合度最好的Copula函数来描述风电场之间的联合概率分布,5种常用的Copula函数与经验分布函数之间的无穷范数ρ=‖·‖∞如附录C表C1所示,其Q-Q图如附录C图C1所示。根据光伏电厂光照强度的历史数据,通过KDE得到光照强度的CDF。风电场风速的联合概率分布和光伏电厂光照强度的CDF分别如附录C图C2(a),(b)所示。 由图1和附录C图C3可知,在相同的迭代初始值和收敛判据下,相较于其他三种算法,MTLM算法所需的迭代次数更少,具有快速收敛的特性。并且,在P-f/Q-U和P-U/Q-f两种下垂控制策略下,MTLM算法均具有良好的适用性,适合不同控制策略下孤岛微电网的概率潮流计算。由附录C表C2和表C3可知,在本文的两种下垂控制策略下,牛顿法对初值的依赖性最强,而MTLM算法最弱,其能适应在更大的初值范围下孤岛微电网的概率潮流计算,具有更强的鲁棒性。进一步,在2种初始值的情况下由附录C图C4可知,MTLM算法通过较少的迭代次数即可收敛至真解,而牛顿法发散;传统单步自适应LM算法不能收敛,但可提供一个最大迭代步下的最小二乘解;改进信赖域算法部分情况下会满足收敛判据(附录C图C4(b)),而此时得到的并非系统真解,只是一个局部最优解,从而验证了MTLM算法的有效性和鲁棒性。 图1 P-f/Q-U下垂控制4种算法的收敛特性Fig.1 Convergence of four methods with P-f/Q-U droop control 基于上述500次QMC模拟获得的负荷及DG出力样本,采用收敛性和鲁棒性更好的MTLM算法进行孤岛微电网的概率潮流计算。基于P-f/Q-U和P-U/Q-f两种不同的下垂控制策略,分别得到系统频率的概率密度函数(probability density function,PDF)和CDF如图2所示;37,38下垂控制节点的电压幅值、流入孤岛微电网的有功功率、无功功率的PDF如附录D图D1至图D3所示;不同下垂控制策略下,系统网损率的PDF如附录D图D4所示。 图2 不同下垂控制策略下频率的PDF和CDFFig.2 PDF and CDF of frequency with different droop control strategies 由图2可知,计及负荷和DG出力的不确定性时,P-f/Q-U下垂控制下系统频率PDF的标准差更小,频率的波动范围很小,而P-U/Q-f下垂控制下频率PDF的标准差比较大,频率波动范围介于0.996(标幺值)到1.004(标幺值)之间。结合附录D图D2可知,在P-f/Q-U下垂控制下,孤岛微电网下垂控制节点有功功率的相对调节范围较小,因此其对应的频率变化范围也较小;同时由附录D图D3可知,P-U/Q-f下垂控制下,下垂控制节点注入的无功功率调节范围大,也对应于图2中频率较大的变化范围。 进一步,结合附录D图D2和图D3可知,P-f/Q-U下垂控制策略下,下垂控制节点输出的有功功率的标准差与P-U/Q-f下垂控制策略相差不大,而无功功率的标准差远小于P-U/Q-f下垂控制策略。在P-U/Q-f下垂控制策略下,下垂控制节点的无功功率与系统频率存在下垂控制关系,而基于潮流平衡方程,无功功率注入又为系统电压稳定提供支撑,因此,下垂控制节点在P-U/Q-f下垂控制策略时提供了较大的无功功率调节范围。在实际分析时,对于计及源荷不确定性的孤岛微电网,需要结合下垂控制系数和系统参数,分析下垂节点有功功率或无功功率PDF的概率分布特征,保证下垂控制DG装置出力具有合理的调整范围,进而为维持系统频率和电压的稳定提供保证。 同时,由附录D图D4可知,在P-f/Q-U和P-U/Q-f下垂控制策略下,系统网损率的均值分别为4.74%和4.72%,二者相差不大;而标准差分别为0.70%和1.24%,P-U/Q-f下垂控制策略下网损率的标准差较大。因此,计及源荷不确定性时,不同控制策略下系统网损率的概率分布特征也有所不同,主要表征为PDF的标准差相差较大。 基于500次QMC模拟获得的负荷及DG出力样本,保持DG随机出力的波动性不变,提高DG有功功率出力样本的期望值,以实现随机性DG有功功率出力接入孤岛微电网的比例增加,DG随机出力相对于总负荷的不同比例情况如附录E表E1所示。在不同比例的具有随机性的可再生能源接入下,采用MTLM算法进行孤岛微电网概率潮流计算,基于P-U/Q-f和P-f/Q-U两种下垂控制策略,分别得到系统频率的PDF如附录E图E1和图E2所示;37,38下垂控制节点电压幅值的PDF如附录E图E3(a),(b)所示。 由附录E图E1至图E3可知,随着随机性DG接入微电网比例的逐步提高,两种下垂控制策略下,系统频率和下垂控制节点电压幅值概率分布的均值和方差均逐渐增大,二者的变化范围均变大。随机性DG在高比例接入时,其流入孤岛微电网的有功功率会增加。因此,下垂控制节点输出的有功功率会减小,在P-f/Q-U下垂控制下,系统频率的变化范围会相应增大,如附录E图E2所示;相应地在P-U/Q-f下垂控制下,下垂控制节点的电压幅值的变化范围会增大,如附录E图E3(b)所示。虽然随机性DG高比例接入微电网时,其无功功率注入也会增加,但是由于孤岛微电网PV节点无功功率注入减小的更多,使得下垂控制节点需要提供更多的无功功率支撑。因此,在P-f/Q-U下垂控制下,下垂控制节点电压幅值的变化范围会相应增大,如附录E图E3(a)所示;相应地在P-U/Q-f下垂控制下,系统频率的变化范围会增大,如附录E图E1所示。 进一步由附录E图E1可知,在P-U/Q-f下垂控制、高比例接入算例3的情况下,系统频率的变化范围已超出频率的安全运行范围(0.996~1.004)。并且结合附录E图E3(b)可知,下垂控制节点的电压幅值仍在安全范围内(0.94~1.06)。表明下垂控制节点的无功功率注入已经超过其无功功率出力的最大值,而有功功率的调节范围还未超过限制。因此,将P-U/Q-f下垂控制策略进行改进,将37,38节点的无功功率静态下垂增益n1qi设置为0.004和0.006,进而使得下垂控制节点无功功率的最大值变大。基于改进的P-U/Q-f下垂控制策略得到系统频率的PDF如附录E图E4所示,进一步计算P-f/Q-U和改进的P-U/Q-f下垂控制下,系统网损率的PDF分别如图3和图4所示。 图3 P-f/Q-U下垂控制下系统网损率的PDFFig.3 PDF of grid loss rate with P-f/Q-U droop control 图4 改进的P-U/Q-f下垂控制下系统网损率的PDFFig.4 PDF of grid loss rate with modified P-U/Q-f droop control 由附录E图E4可知,改进的P-U/Q-f下垂控制下,下垂节点的无功功率限制增大,随着随机性DG接入比例的提高,系统的频率能够保证在安全范围内变化。由图3和图4可知,随着DG接入比例的提高,系统网损率的概率分布逐渐向左移动。在P-f/Q-U下垂控制下,算例1至算例3系统网损率的均值分别为5.20%,4.74%和4.00%;在P-U/Q-f下垂控制下,系统网损率的均值分别为5.50%,4.72%和3.83%。随机性DG接入微电网的比例提高后,系统有功功率分布式消纳的能力增强,有功功率不再仅以下垂控制节点的注入为主,而是进一步从随机性DG接入的节点分布式注入,因此,降低了线路传输的有功损耗。 本文计及可再生能源的不确定性,基于P-f/Q-U和P-U/Q-f两种下垂控制策略,建立了综合控制下孤岛交流微电网的概率潮流计算模型,并提出了一种MTLM算法对潮流方程进行求解。通过研究分析得到如下结论。 1)相比牛顿法、传统单步自适应LM算法、以及改进信赖域算法,本文所提的MTLM算法具有更快的收敛速度和更强的鲁棒性,适用于孤岛交流微电网的概率潮流计算。 2)计及可再生能源不确定性时,不同的下垂控制策略均能够维持孤岛微电网的频率和电压稳定,但不同的下垂控制策略及其下垂控制参数对系统频率、下垂控制节点电压幅值、以及系统网损率的概率分布均有一定的影响,并以PDF的标准差为表征。 3)在下垂控制节点可维持的系统频率和电压稳定范围内,随着具有随机性的可再生能源接入孤岛交流微电网的比例增大,可再生能源进一步就近分布式消纳,有利于减少线路总的传输功率,降低系统网损率均值。 随着电网内不确定性因素的增多,本文所提MTLM算法可为其他电网结构下的概率潮流计算问题提供参考,尤其在交直流混合的电网结构下,探索MTLM算法的收敛特性是下一步研究的方向。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。3 基于QMC模拟的概率潮流计算
3.1 相关性生成
3.2 孤岛微电网概率潮流计算流程
4 算例分析
4.1 算例系统
4.2 算法对比
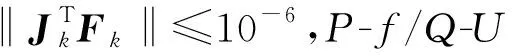

4.3 控制策略分析
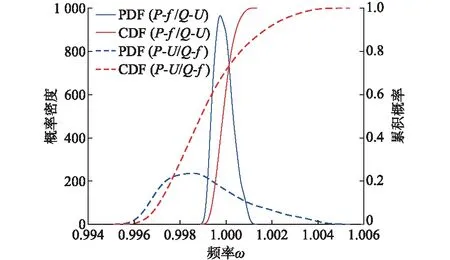
4.4 不同比例可再生能源接入下的系统分析

5 结论
