考虑故障限流器动作的直流电网限流电抗器优化配置
2018-08-09朱思丞赵成勇李承昱许建中
朱思丞, 赵成勇, 李承昱, 许建中
(新能源电力系统国家重点实验室(华北电力大学), 北京市 102206)
0 引言
模块化多电平换流器(MMC)型柔性直流电网技术近些年受到广泛的关注[1-5],是光伏发电和风力发电等新能源大规模接入电网的重要技术手段[6-7]。在直流电网发生直流故障瞬间,换流器子模块电容向故障点快速放电,导致直流电流迅速增大,直流电压下降,从而对直流电网系统造成严重危害[8]。直流电网保护系统需要具备极高的响应速度。
在直流故障发生后,故障限流器(fault current limiter,FCL)可以一定程度地限制故障电流上升,直至故障线路切除,可以使故障电流保持在系统允许范围内,并且降低对直流断路器切除故障动作时间、开断容量等方面的要求,有助于直流侧故障的安全可靠隔离,提高直流系统可靠性[9]。
很多学者对直流系统限流措施做了相应研究。文献[10]提出在多端柔性直流系统中通过增加电感的方法来抑制直流侧故障电流,但并未对限流特性进行分析,且电感参数的选择方法缺乏一定理论依据。直流断路器切除故障后,限流电感中的能量无法释放,容易产生过电压,影响换流站设备的绝缘。文献[11]提出通过在直流线路两端串入限流电路的方法来限制故障电流的峰值和电流的上升速率,并给出相关参数的理论计算方法。文献[12]对直流断路器的限流控制进行了分析,指出在系统参数一定的情况下,限流参考值的大小直接影响避雷器吸收能量的多少。文献[13]提出了一种带有限流功能的高压直流断路器拓扑,采用晶闸管作为主开关器件。限流电抗器采用分散布置。在稳态运行时并联,对外呈现低电抗值;在故障时串联,具有较好的故障电流抑制效果,便于主断路器件切除故障。
在发生直流线路发生故障后,换流器出口侧的固有直流电抗器可以起到降低故障电流上升率的作用。但是直流电抗器参数选取得越大会对系统稳定性、动态特性造成不利的影响,甚至可能会导致整个直流系统某些模态呈现弱阻尼[14],另一方面会增大直流电网的建设成本。研究在直流系统固有的直流电抗和额外投入的限流电抗总和恒定的情况下,合理分配直流电抗和限流电抗的参数具有一定意义。
上述文献所提出的限流方法,并未涉及含故障限流器投入限流电抗后的故障电流特性和直流断路器切断过程的能量耗散问题。本文考虑了故障限流器并联的金属氧化物避雷器(metal oxide arrester,MOA)的能量耗散特性,以及直流断路器切断故障电流时的能量耗散特性,分析了故障电流特性。
本文针对多端模块化多电平换流器型柔性直流电网系统,采用单纯形法(simplex),对各个直流出口侧故障点,以直流断路器切断故障电流值最小与故障限流器和直流断路器中MOA吸收的能量之和最小为多目标进行优化,并给出了不同权重下,各条直流线路的直流电抗器优化配置方案。
1 考虑故障限流器动作的单端MMC故障电流特性分析
直流双极短路故障是直流电网中最严重的故障类型[15]。当换流站线路出口侧发生双极短路故障时,故障电流最为严重。
1.1 双极短路故障时故障电流特性
1.1.1双极短路故障时单端MMC等效电路
直流电网中双极短路故障发生后的几个毫秒内,交流馈入的短路电流相较于子模块电容放电电流而言可以忽略不计。同时,假设换流器不闭锁,以传统半桥MMC为例,此时的故障等值电路如附录A图A1(b)所示[16]。图中,R0为一相桥臂电阻(由放电回路中的二极管和IGBT的通态电阻串联组成);L0为桥臂电抗器;Ldc为直流电抗器;Req,Leq和Ceq分别为故障等值电路中的电阻、电感和电容。其中,图A1(b)所示具体电路参数计算如下:
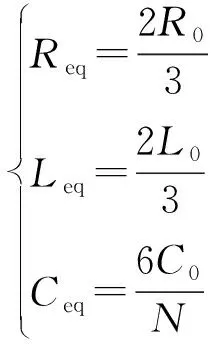
(1)
式中:C0为子模块电容值;N为一相桥臂子模块数。
由于架空线的对地电容很小,忽略对地电容的影响,将直流线路化简为R-L的串联结构。
1.1.2双极短路故障电流方程

一般情况下,(R/2L)2≪1/LC,可求得回路故障电流if的计算公式为:

(2)
式(2)中的各个变量可由以下电路参数决定:
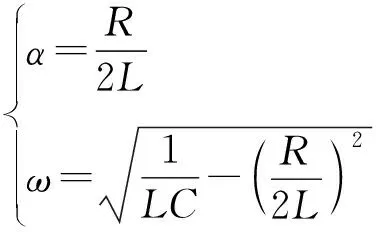
(3)
由式(2)可得,故障电流if为(L,Iin)的函数。
1.2 考虑故障限流器动作的故障电流特性
1.2.1投入限流电抗器后的等效放电回路
检测到在t0时刻发生直流故障后,故障限流器动作,在t1时刻等效地投入的电感值为LF。在t2时刻完全投入限流电抗后,在t3时刻直流断路器切断故障电流。忽略故障限流器自身内部的动作对故障电流的影响。
MOA可以有效地保护电力系统中的设备避免遭受过电压而发生故障甚至损坏,金属氧化物压敏电阻(metal-oxide varistors,MOV)是MOA中的限压元件,它吸收过电压能量的能力和限制过电压的效果决定了MOA的主要性能,本文中耗能元件缩写采用MOA。故障限流器在投入电抗器的过程中,故障限流器两端并联的MOA也会触发激活,吸收一部分的能量,防止产生严重的过压。MOA的伏安特性可以用分段函数特性来表示[17],其伏安特性曲线如附录A图A2所示,其中基准值为MOA的额定电压UMOAn。
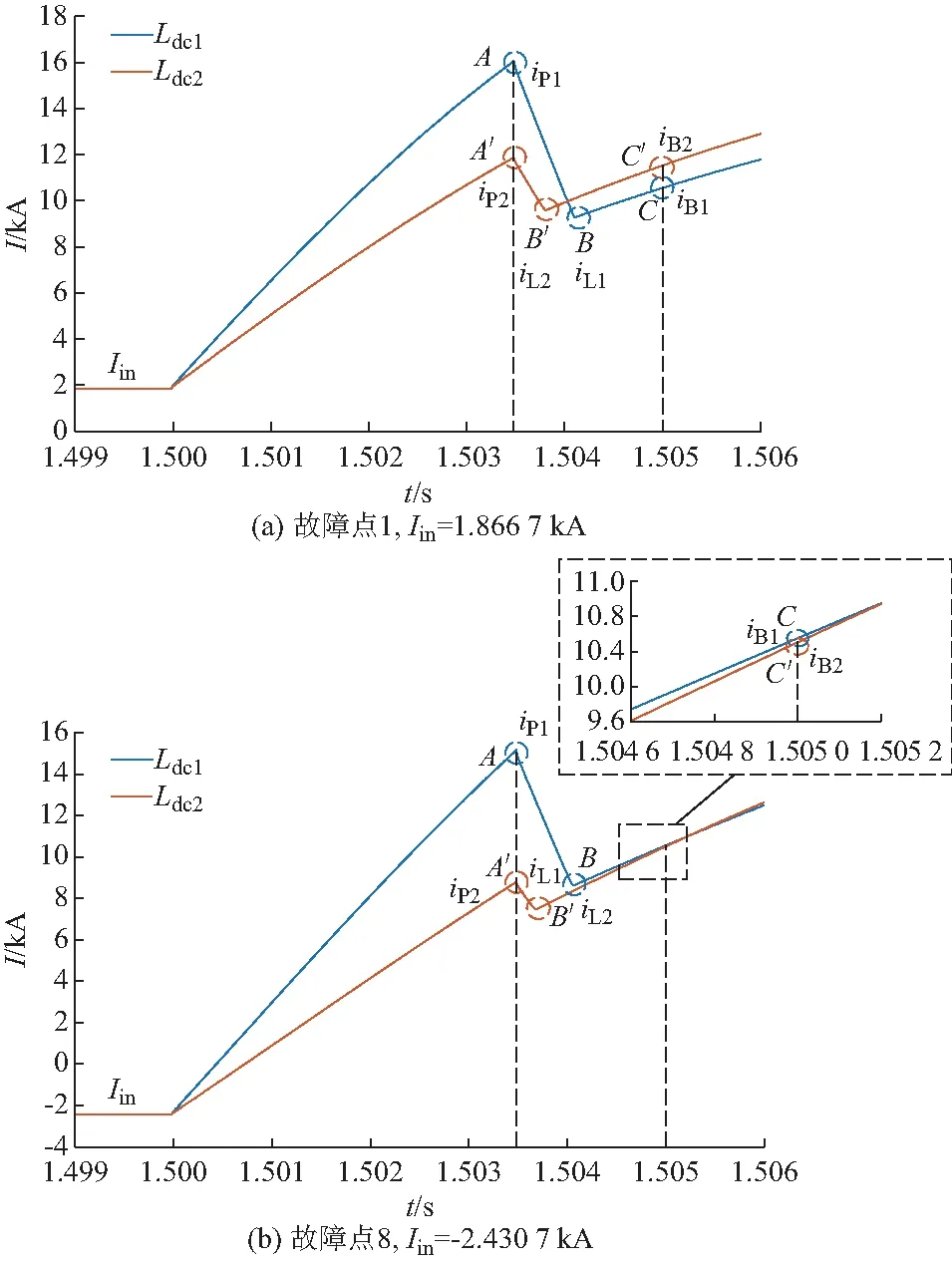
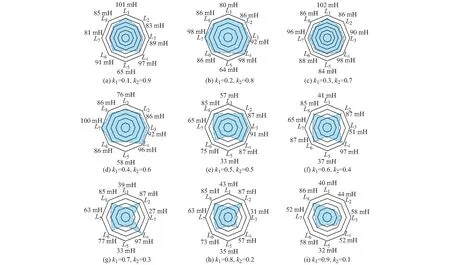
MOA的两端的电压和流过的电流分别记为uMOA和iMOA。当uMOA 考虑含并联MOA的故障限流器投入放电回路的等效简化电路如附录A图A3所示。 此时故障回路的电流记为if,流过故障限流器的电流记为iF。其中,iMOA与if满足: if=iMOA+iF (4) 且uMOA与iMOA满足: (5) 1.2.2不同直流电抗器和限流电抗器配置下的故障电流分析 在保证直流线路出口直流电抗器电感Ldc和故障限流器电抗器电感LF之和(Ldc+LF记为直流侧总电抗)不变的前提下,分析直流电抗器和故障限流器中电抗在不同配置下的故障电流情况。 在t1时刻故障限流器投入限流电抗器,Ldc1,LF1和Ldc2,LF2分别为两组直流电抗器和故障限流器的电感值,电流分别对应为i1和i2。其中,满足Ldc1+LF1=Ldc2+LF2,且Ldc1 以图1所示的双极结构的四端直流电网拓扑为例。图1中一共有1~8个直流侧出口故障点。直流电网单站MMC参数见附录A表A1所示。 直流电网稳态电流方向如图1所示。当架空线路采用R-L模型时,根据式(1)的等效方法和图1中的参数,单站的等效Ceq,Req,Leq参数见附录A表A2所示。 图1 四端直流电网拓扑Fig.1 Topology of four-terminal DC grid R-L线路参数设置为RL=0.01 Ω/km和LL=0.82 mH/km。在t0=1.5 s时发生双极短路故障,考虑故障检测和故障限流器投入限流电抗器的时间t1=1.503 5 s,考虑故障限流器作用后直流断路器的动作时间t3=1.505 s,直流侧总电抗可取150 mH。 根据图2所示,在同一个t1时刻电流拐点A和A′处,iP1>iP2,iP为限流器投入电抗时刻的电流值。根据不同的电流初值Iin,iL1和iL2的大小会有不同,iL为限流器的MOA退出运行时的电流值。直流断路器切除故障电流时,存在一个电流值Ith(Ith约为零附近的一个值),若Iin>Ith,在t3时刻切断故障电流,此时iB1 直流断路器以ABB公司提出的混合式高压直流断路器为例[18]。其工作原理为:在正常运行时,电流只流过由负荷转换开关与快速机械式隔离开关组成的支路一,主断路器中电流为零。当直流侧发生故障时,负荷转换开关打开将电流转换到主断路器支路中,同时将快速隔离开关打开,待快速隔离开关完全打开,主断路器断开故障电流。成功分断后,隔离开关断开较小的剩余电流,完成故障线路隔离。 根据该直流断路器的工作原理可知,与图A3中故障限流器并联MOA不同在于,其主断路器分断故障电流的过程可以近似地等效为分断时将主断路器的避雷器组串联接入故障回路,从而故障电流在主断路器的MOA中耗散至零。 根据故障限流器投入后故障电流的变化特性,附录A图A4为故障限流器和直流断路器动作的时序,直流断路器在故障限流器动作起作用后切断故障电流,有效地降低了切断时的电流大小。 图2 R-L线路模型下的不同直流电抗器和限流电抗配置故障电流仿真波形Fig.2 Fault currents simulation waveforms under various configuration of DC reactors and FCLs based on R-L line model 直流输电线路是直流电网系统的重要组成部分之一,由于中国直流输电的架空线路较长,直流电压等级高,输电线路的稳态和暂态特性对整个直流系统的特性影响较大。第1节中线路模型采用的是R-L模型,不能反映输电线路的暂态特性。下面将着重讨论基于相域频变线路模型的故障电流特性。 目前常使用的输电线路模型包括四种:PI结构模型(PI section model)、贝杰龙模型(Bergeron model)、模域频变模型(Frequency Dependent (Mode) model)、相域频变模型(Frequency Dependent (Phase) model)。PI结构模型是集中参数模型,不能反映线路的分布参数特性;贝杰龙模型是基本的行波模型,可以等效为无穷多个短PI结构模型,但只能反映某一固定频率下的线路特性;模域频变模型和相域频变模型考虑了输电线路的频变特性,包含了所有参数的频率相关特性,但是相域频变模型相较于前者,直接在相域中对输电线路的频变特性进行拟合,避免了相模变换带来的误差,使得线路模型更准确[19]。 相域频变模型是目前为止最为精确的线路模型,模型中的电阻、电感、电容均为分布参数,广泛应用于各种电磁暂态仿真中。相较于第1章中所用的R-L线路等效模型,相域频变模型可以更精确地反映直流故障后的暂态特性。下面将采用相域频变线路模型分析含故障限流器动作的故障电流特性。 直流架空线路模型为PSCAD/EMTDC中的相域频变模型。 同样地,分别选择故障点1(Iin=1.864 4 kA)和故障点8(Iin=-2.449 2 kA),由于R-L线路模型和相域频变线路模型稳态参数不同,所以直流电网稳态时的电流会略有不同。在保持直流侧总电抗恒定的情况下,分别取Ldc1=50 mH和Ldc2=100 mH两组直流电抗配置方案,仿真得到故障后的故障电流波形。其中,在t0=1.5 s时发生故障,考虑1.5 ms[9]的直流电网故障检测时间,故障发生后3.5 ms投入限流电抗器,即t1=1.503 5 s。得到两组电流波形如图3所示。 图3中的线路模型为相域频变模型,保证了结果的精确度。与图2相比,在投入故障限流器直到直流断路器切断故障电流的过程,仍然有A,B,C这3个拐点,即在不同的电流初值Iin下,结论仍与图2中的相同。由此可得,在直流侧总电抗恒定的情况下,不同的直流电抗器和限流电抗器配置对直流断路器的切断电流大小以及故障限流器中并联MOA和直流断路器主断路器中的MOA能量耗散特性有一定的影响。 在保持直流侧总电抗为150 mH恒定的情况下,直流电抗器取值范围在20 mH~130 mH,以1 mH为步长,选取故障点1和故障点8,得到在不同直流电抗器配置下的故障限流器投入时的电流值iP和同一时刻直流断路器切断时的电流值iB,以及故障限流器和直流断路器中MOA的能量,如附录A图A5所示。其中QMOAC,QMOAF和QMOAS分别代表直流断路器的能量、故障限流器中MOA的能量以及两者能量之和。 由附录A图A5可得,随着直流电抗器Ldc的增大,iP的逐渐减小,但是根据不同的电流初值Iin,随着Ldc的增大,iB均会出现图3所示的两种情况;QMOAS的值随Ldc的增大而逐渐减小。根据这些量随着Ldc增大而变化的情况,可以进行直流电抗器和限流电抗器配置的优化。 图3 相域频变线路模型下的不同直流电抗器和限流电抗配置故障电流仿真波形Fig.3 Fault currents simulation waveforms under various configuration of DC reactors and FCLs based on frequency dependent (phase) model 直流电抗器和故障限流器对直流电网的故障隔离具有重要的作用。从故障限流的角度而言,由以上的分析可知,在直流侧总电抗恒定的情况下,随着直流电抗器电感值的增加,同一时刻投入限流电抗器时的故障电流会不断减小,但是对于不同的电流初值Iin,同一时刻直流断路器切断的电流会不同,而且在不同的直流电抗器参数下,故障限流器并联的MOA和直流断路器切断故障电流时主断路器的MOA中的能量情况也会不同。 MOA吸收的能量根据图A2所示的伏安特性和焦耳定律可以求得: (6) 式中:QMOA为MOA吸收的能量;tb为MOA在电路中作用的时间。 根据式(2)和式(3)可知,直流电抗器Ldc(或限流电抗器LF)的配置决定了故障电流值的大小。又根据式(4)—式(6)可知,直流电抗器Ldc的配置影响了MOA中吸收能量的大小。 全网直流断路器切断电流以及故障线路中耗能元件MOA中的能量尽可能地小,可减小直流断路器的切断容量以及防止MOA的热超载。本文优化目标为使得直流断路器的切断电流iB和故障限流器和直流断路器的MOA吸收的能量之和QMOAS尽可能取值小。5 ms直流断路器开始断开故障电流。以在5 ms内能开断15 kA的直流断路器为例[20],且要求直流电流Idc不大于额定直流电流Idcn的3倍[21],Udcn取500 kV,Pn取3 000 MW,则要求Idc≤18 kA。直流断路器切断时的故障电流应小于限流电抗器投入时的电流,即iB (7) 式中:iBi和iPi为各个故障点的电流。 对于多目标优化,可以采取变动权系数法[22]。分别给多目标函数F的各分量fi以权系数ki(i=1,2)。作线性加权和评价函数,为: (8) 把问题归结为求解问题: minF (9) 一般在作式(8)目标函数线性和时,要先将fi规范化。一般采取式(10)的处理方法: (10) 本文采用simplex优化算法,simplex算法是基于几何形状考虑的启发式优化算法。在n维空间中,单纯形是指以n+1个顶点所构成的最简单图形。单纯形算法不是沿一个方向进行搜索,而是对n维空间的n+1个点(单纯形的顶点)上的函数值进行比较,舍弃其中最坏的点,代之以新的点,从而构成新的单纯形,逐步逼近最优点[23]。 结合上述的含故障限流器动作的直流电网故障电流分析情况,对图1所示的四端直流电网进行直流电抗器和限流电抗器的配置进行多目标优化。 目标函数通过罚函数进行修正,本文罚函数因子选取为M=107。目标函数修正为: minF′=minF+M(min[18-iB1,0])2+…+ M(min[18-iP1,0])2+…+ M(min[iP1-iB1,0])2+… (11) 式中:min[a,b]表示取a和b中较小的值。 仿真采用PSCAD/EMTDC仿真程序中的“Optimum Run”元件中的simplex优化方法,如图1所示的四端直流电网中,各直流线路侧出口编号为1~8共8个故障点分别设置双极短路故障。 当k1=1,k2=0和k1=0,k2=1时,即分别以各个故障点切断电流之和最小(f1,min)和各个故障点故障限流器和直流断路器的MOA能量之和最小(f2,min)为单目标求解,分别求得单目标f1,min=86.756 0 kA和f2,min=163.764 5 kJ。各位置直流电抗器配置见图4。 图4 单目标优化下的直流电抗器配置Fig.4 DC reactors configuration under single-objective optimization L1至L8依次为图1中1~8个直流侧出口的最优直流电抗器配置,相应地根据直流侧总电抗值恒定为150 mH可以得到故障限流器的限流电抗器的配置。根据图4的直流电抗器优化配置图,以f1,min为例,各个直流侧出口的最优直流电抗器和故障限流器配置如附录A表A3所示。由图4可得,以各个故障点切断电流之和最小为目标与以故障限流器和直流断路器的MOA能量之和为目标相比,优化求解得到的各条直流线路的直流电抗器配置总体偏小,即限流电抗器的配置总体偏大。对于L1,L2,L7,L8这4处电流初值Iin较大的故障点,不同目标函数下最优直流电抗器配置变化较大。 根据式(7)至式(11)的多目标最优化方法,以0.1为步长,分别取k1=0.1~0.9,得到9种不同权重下的各条直流线路直流电抗器的优化结果,如图5所示。 图5所示的结果可以根据表A3得到不同权重下的直流电抗器和故障限流器的最优配置。以k1=0.1,k2=0.9为例,直流线路各个直流电抗器的最优配置L1至L8分别为:101,83,89,97,65,91,81,85 mH;相应的故障限流器的最优配置为:49,67,61,53,85,59,69,65 mH。 图5 多目标优化下的直流电抗器配置Fig.5 DC reactors configuration under multi-objective optimization 不同的权重代表了对不同目标的侧重程度,在实际工程或者特殊场合,直流断路器切断故障电流大小与直流电抗器和限流电抗器中的MOA吸收的能量大小的重要程度不一定相同,则两者的权重取值可以根据需要选取。 本文研究了含并联MOA的故障限流器动作时的故障电流特性,并讨论了在R-L线路模型下,不同电流初值Iin下的故障电流情况。基于相域频变架空线路模型,在PSCAD/EMTDC仿真程序中验证了不同电流初值Iin下的故障电流情况。 在四端双极直流电网中,对8个直流出口侧故障点,以直流断路器切断故障电流大小之和与故障限流器和直流断路器中MOA吸收能量大小之和最小作为目标函数,采用simplex算法对直流电网中各条直流线路的限流电抗器进行优化配置,并给出了不同权重下的各条直流线路的限流电抗器优化配置方案。 本文在考虑直流电抗器过大导致的直流系统稳定性、动态特性等问题,以及相应的经济成本,在保证直流侧总电抗恒定的前提下,为直流电网系统合理设置固有直流电抗器和故障限流器的参数提供了理论依据。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。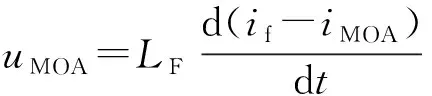

1.3 考虑直流断路器动作的动作时序
2 基于相域频变模型考虑故障限流器动作的故障电流特性
2.1 直流系统输电线路模型
2.2 相域频变模型下含FCL动作的故障电流特性

3 直流侧直流电抗器和限流电抗器的参数优化配置
3.1 优化目标函数


3.2 多目标优化

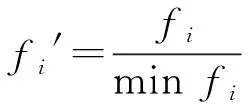
3.3 直流电抗器和限流电抗器优化算例验证

4 结论
